統計検定1級で統計数理と統計応用ともに大問レベルでの出題が予想されるノンパラメトリックに関する数多くの手法を『データ解析のための数理統計入門』を通して学びます。
本記事の内容は大変ボリュームが多いため、各節のまとまりごとに区切って学習します。本記事では内容を区切っていますが、それでもかなりの量です。各節1つ1つがすべて重要な内容ですので、お互いにゆっくりと学び実力をつけていきたいところですね。
データ解析のための数理統計入門の第16章『分布によらない推測法』の例題と解説
経験分布関数
経験分布関数という内容を学習します。これはノンパラメトリックつまり標本データにのみ基づいて構成できる分布関数であり、データが増加すると真の分布関数に収束することから大変便利な考えです。この経験分布関数を用いて標本分位数を求めることができます。またノンパラメトリック検定への応用として利用されます。

ヒストグラム
ヒストグラムの階級の幅についてスタージェスの公式というものがあります。
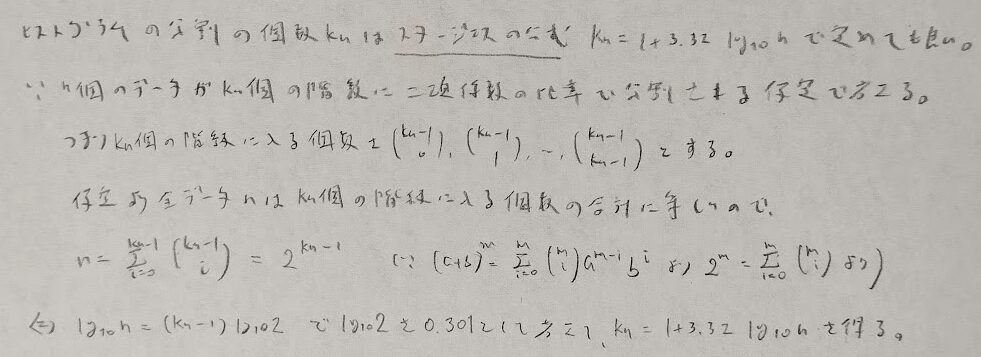
次にヒストグラムを関数で当てはまることを考えます。あまり類書では馴染みがない部分だと思い、まずは定義から解説し次に例を通して下記に書かれている細かい内容を証明していきます。

それでは上記にあった細かい箇所を順に証明します。
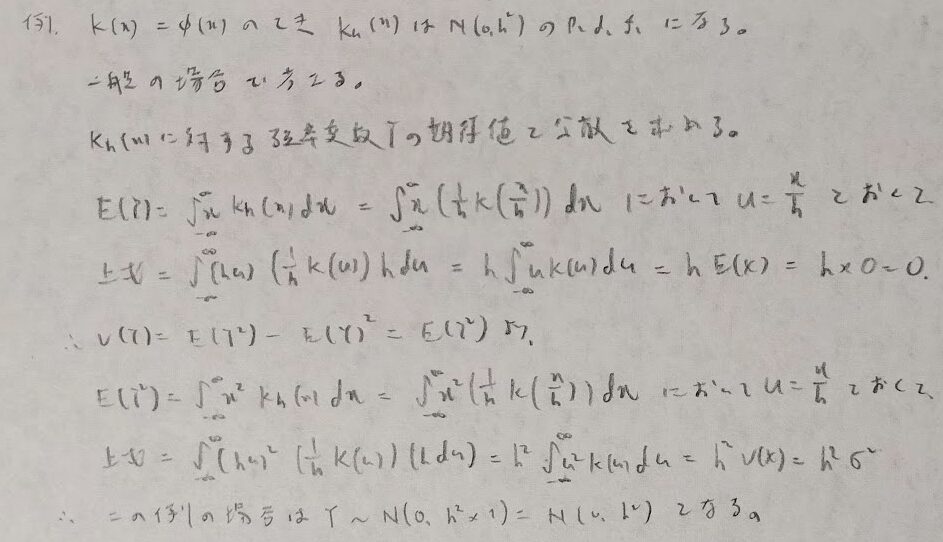
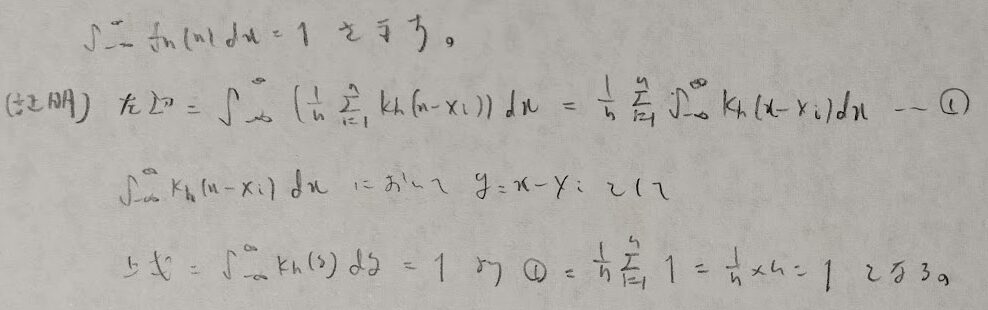
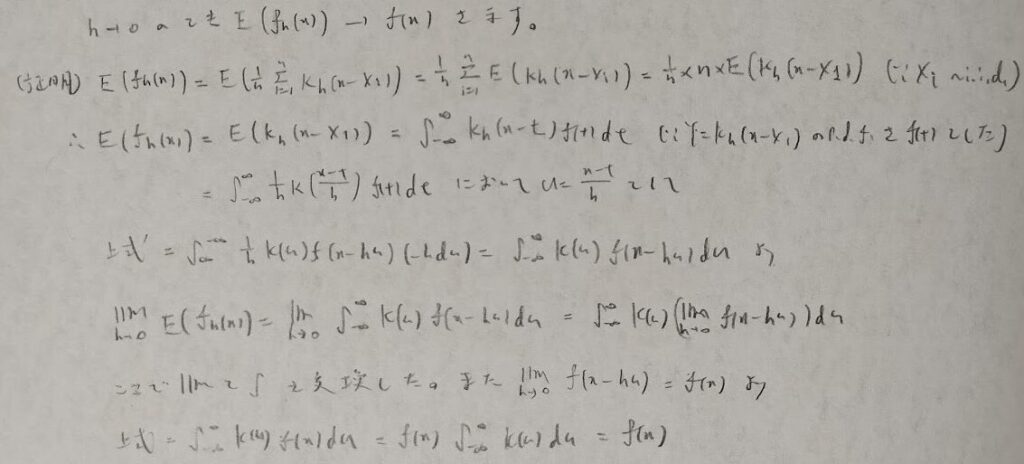
極限操作と積分操作の入れ替えは下記の根拠に基づいています。
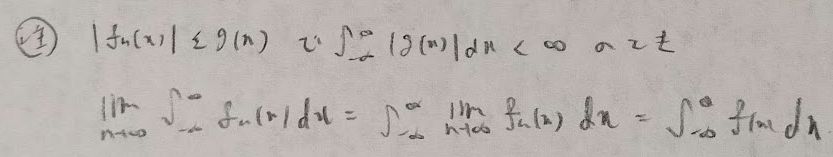
分布の中心の測定
次にM推定量を学習しますが、その一部である標本平均とメディアンについて学びます。
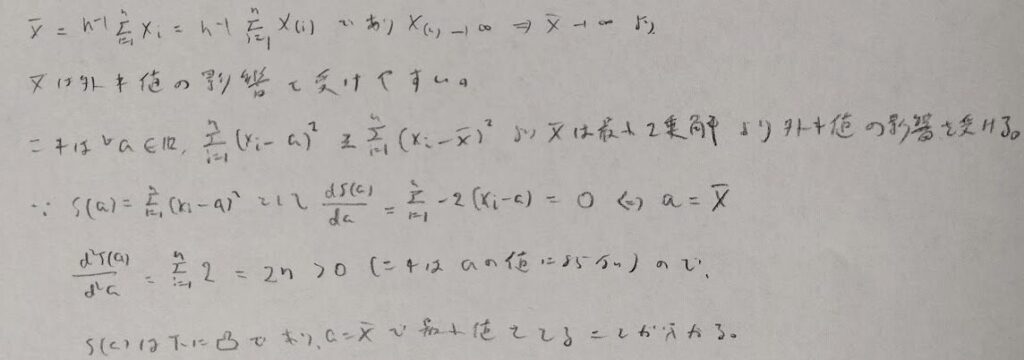
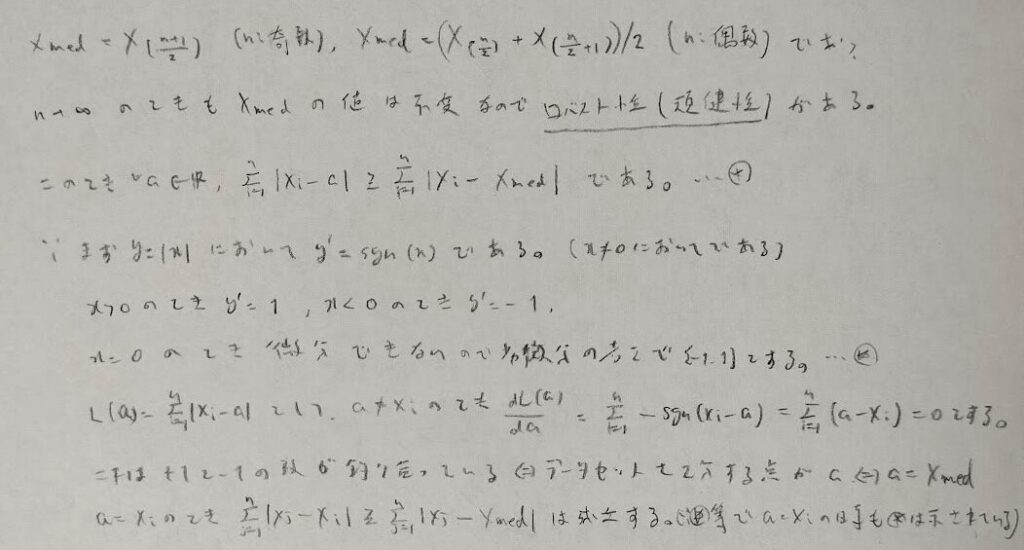
劣微分は尖点での微分の扱いについて補強的な意味合いで用いただけです。重要なのはメディアンもある数式を最小にする量であるということです。
他に分布の中心を表す量はありませんか?
刈り込み平均というものもあります。

それではこれらの概念を一般化します。

M推定量は損失関数Ψ(プサイ)を最小にする量でスコア関数ψ(プサイ)を用いた式が0になる解として求まります。これらの関数をどのように設定するかで標本平均やメディアンなどが次々と導出されるわけです。
ヒストグラムを描いた時に最も高い柱について、その底辺の中点、もしくはその中に入るデータの平均値をXmodeと書き、モード(最頻値)と言います。単峰で右に歪んだ分布では、最頻値<メディアン<標本平均となります。
正のデータに対する有名不等式の大小
次の調和平均≦幾何平均≦算術平均は非常に重要です。統計検定1級でもここに関連する出題があります。

分布のばらつきの測定
ここでは高校時代(早ければ中学数学)で学習する箱髭図などで登場する考えをより深めます。分散に相当するばらつきにあたる標本分散は外れ値の影響を大きく受けます。それでは外れ値の影響をあまり受けないロバストなばらつきの指標とは一体なんでしょうか。
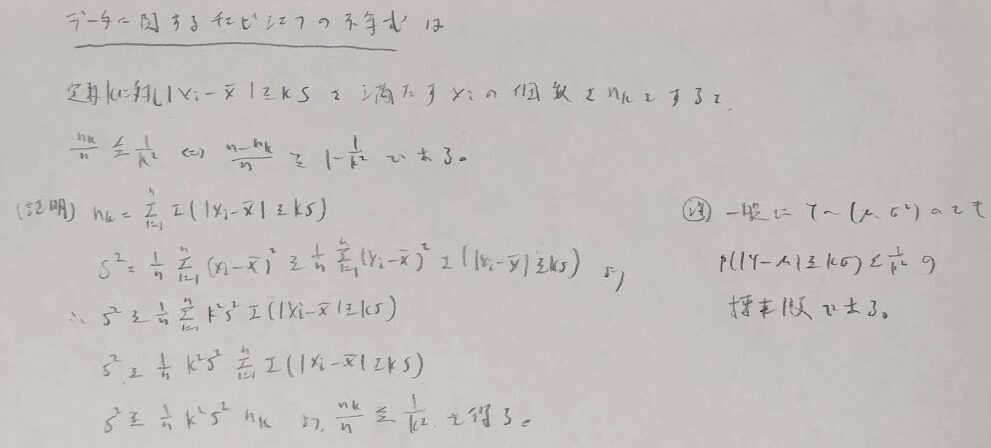
こちらは通常のチェビシェフの不等式がマルコフの不等式から導かれることを思い出せばすんなり証明できるはずです。
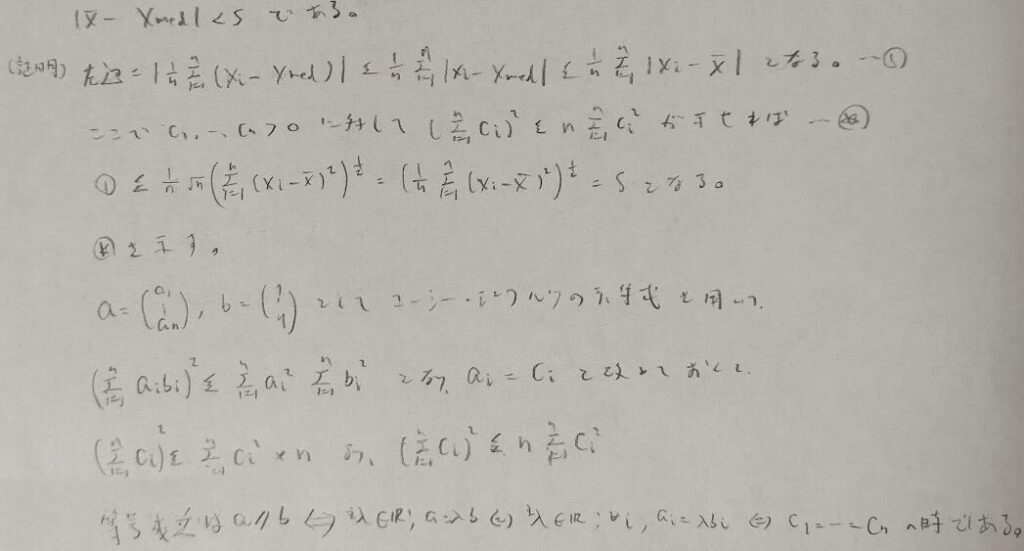
これは初めて見ました!
僕もそう思います。『データ解析のための数理統計入門』に載っていて面白い関係式だな!と思いました。
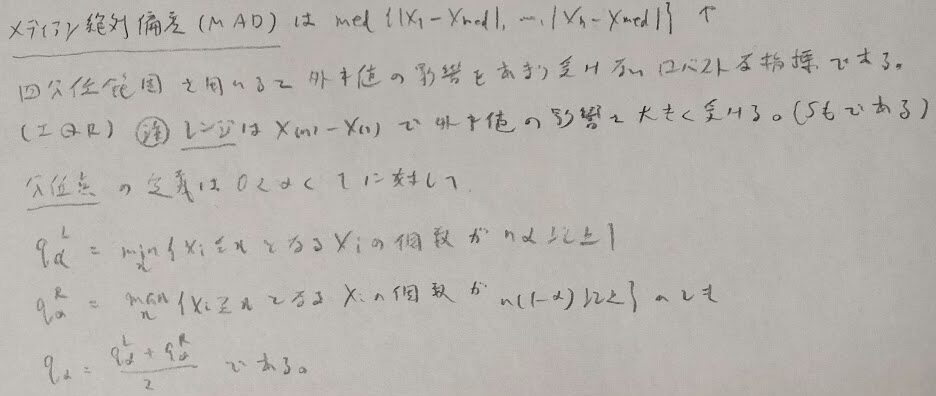
分位点の定義はかなりわかりづらいですが、例えば1〜10までの数字のメディアンは?などと具体的に考えれば合点がいくはずです。
順位相関係数
ここでは標本を用いた3つの相関係数を解説します。まずはピアソンの標本相関係数です。最もポピュラーですが、外れ値に影響を受けやすいデメリットがあります。
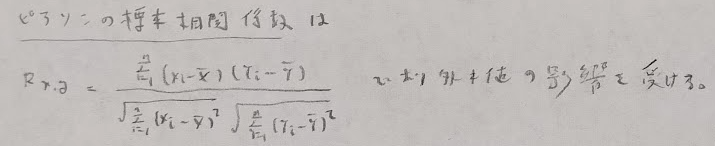
外れ値の影響を受けにくいロバストな方法ではスピアマンの順位相関係数があります。小さい値から順位をつけていくことに注意しましょう。

ケンドールの順位相関係数もロバストな方法です。こちらは符号を重視した方法になります。ピアソンの標本相関係数からは最も考えが遠い方法だと感じています。

ノンパラメトリック回帰とナダラヤ・ワトソン推定量
単回帰分析などではなく未知の回帰関数を考える場合はノンパラメトリック回帰となります。その推定量がナダラヤ・ワトソン推定量です。先ほど学習したカーネル関数が絡んでくるため難易度は非常に高いです。統計検定1級ではいくつかの式が与えられて積分計算を計算できれば正解という問題以上は難易度が高すぎるため、頻度は高くはならないと予想しています。
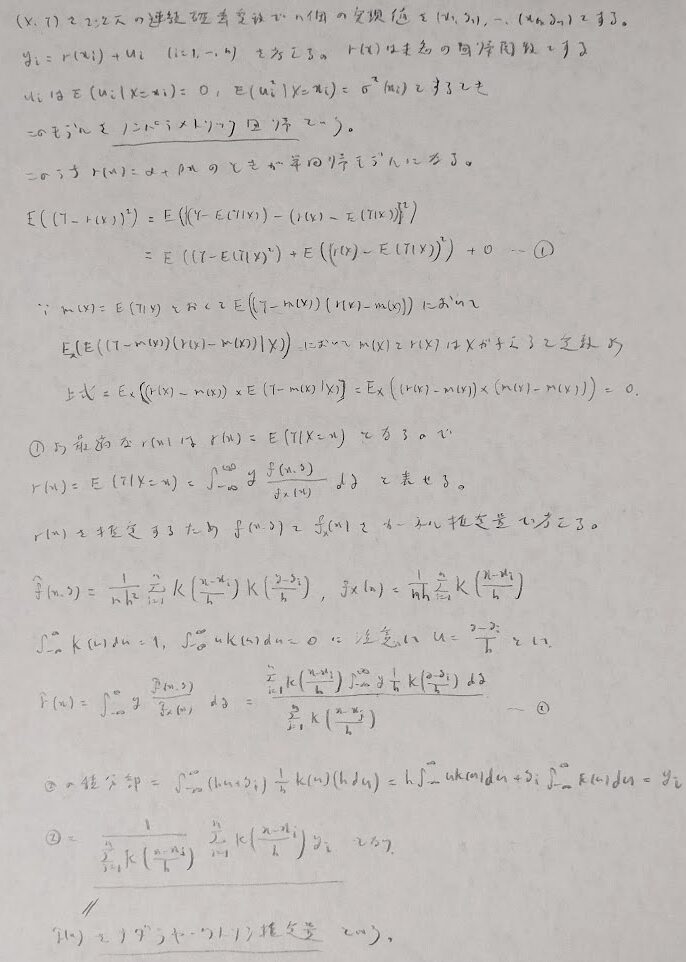
ブートストラップ法
本章で唯一、細かい証明部分がわからず結果のみを書いてしまった箇所が終盤にある節です。そこの部分は非常に難易度が高いため、証明は統計検定1級でも出ないと思われます。
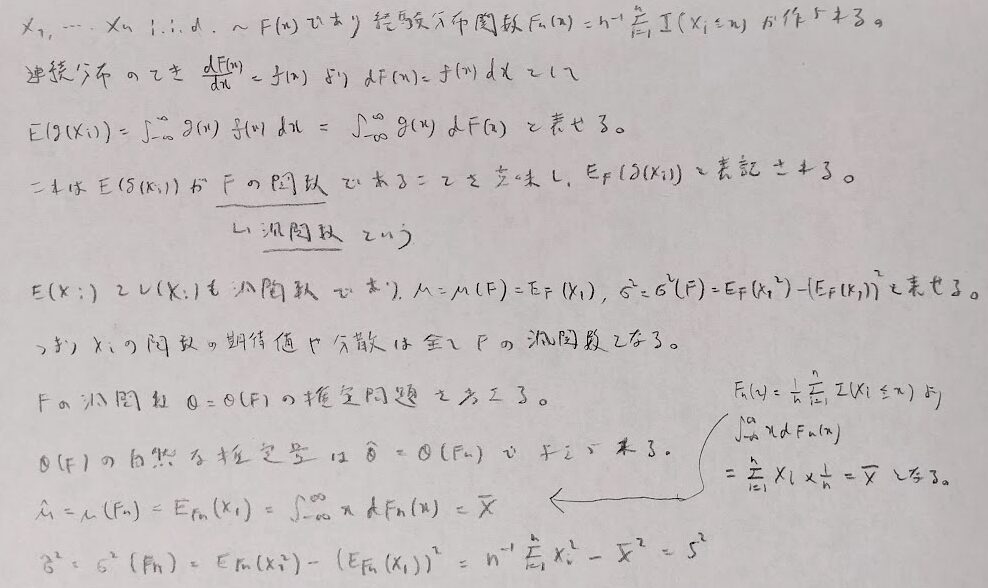
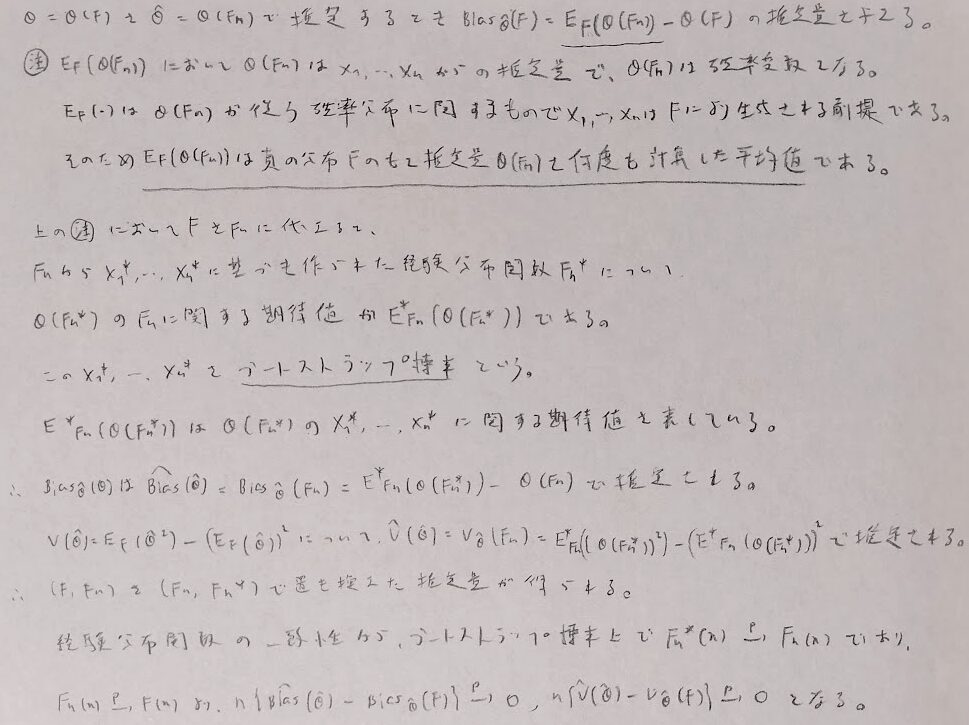
ここの最後の2ヶ所の0に確率収束する部分の証明がわかりませんでした。

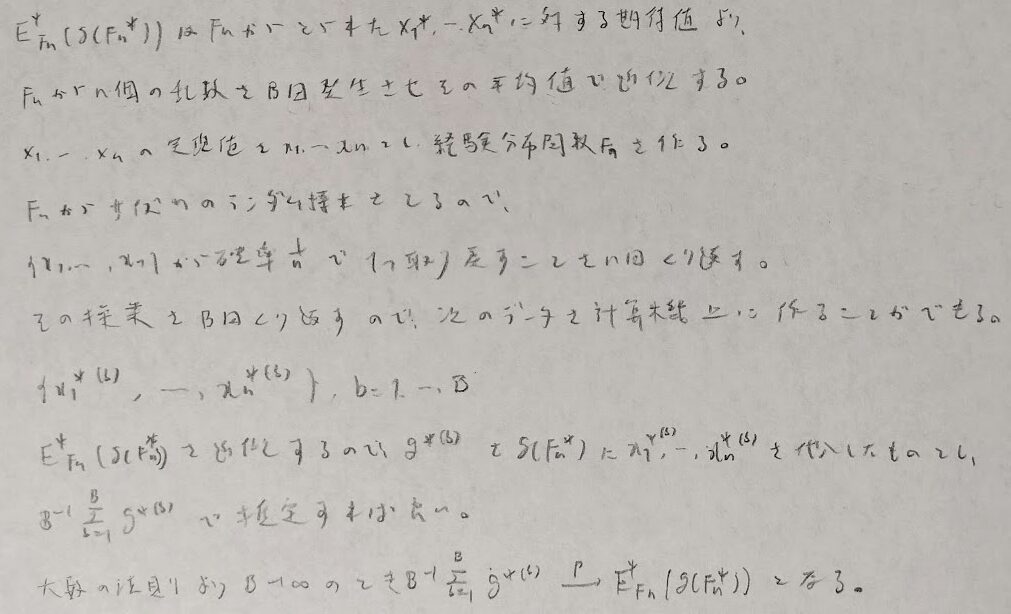
ここでは2つの具体例を示します。
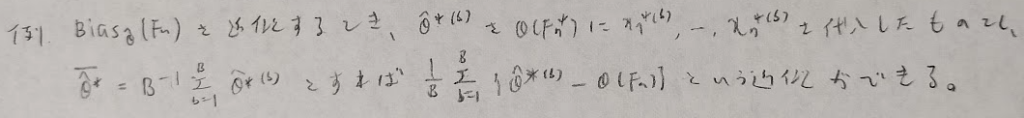
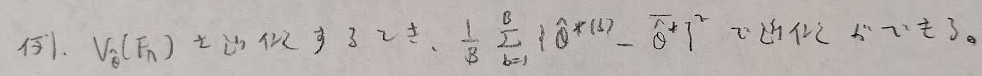
最後にブートストラップ信頼区間について復習します。

ノンパラメトリック検定
符号検定(シンプル)→符号付き順位和検定(より詳しく)→ウィルコクソンの順位和検定(2群)→クラスカル・ウォリス検定(3群以上)→コルモゴロフ・スミルノフ検定(グラフの同一性)→蓮検定(ランダム性)の流れのイメージで進めます。
もっとも単純な符号検定からはじめます。

符号検定だけでは細かい部分まで把握できないことのデメリットを解消した検定が次の符号付き順位和検定です。

次は一般的な2群の関係を考えます。ウィルコクソンの順位和検定(マン・ウィットニー検定)を扱います。

3群以上に適用できる1元配置モデルのノンパラメトリック版であるクラスカル・ウォリス検定を学びます。

分布が等しいことを検定したいときに汎用的に用いることのできるコルモゴロフ・スミルノフ検定を学びます。

最後のα関連がどこから来たのか不明のままで解説ができませんでした。僕自身が理解できたら追記します。
ランダム性について検定できる連検定を学びます。こちらはとても興味深い検定法です。

ここで1つ興味深い問題を紹介します。
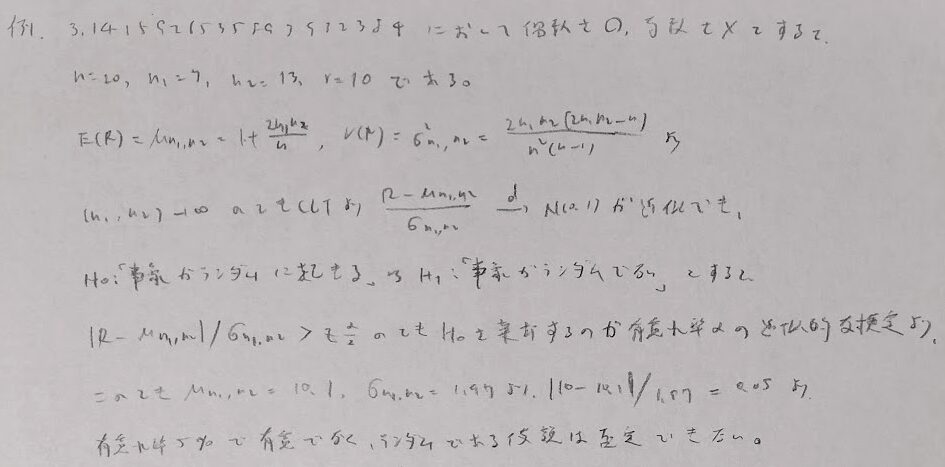
生存時間解析
生存時間解析の理論を学びます。つまりハザード関数を用いて確率密度関数や分布関数、生存関数が表現できることを学び、そして生存関数を推定するカプラン・マイヤープロットを学習します。
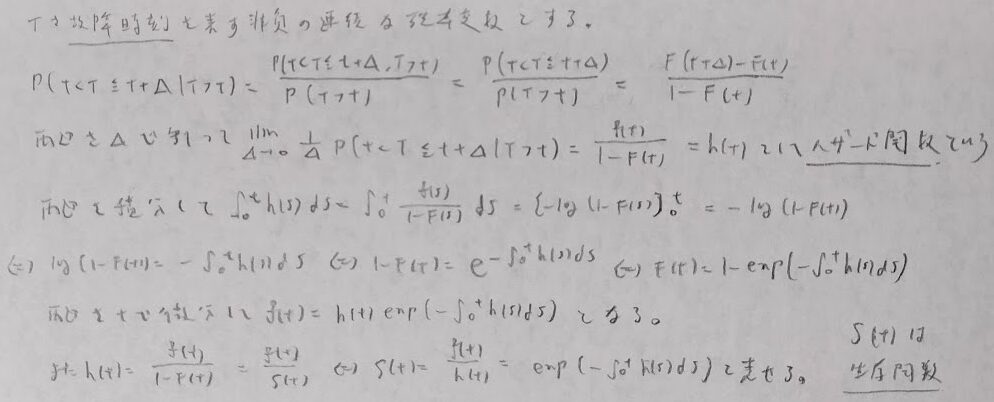
ハザード関数に自然な設定を取り入れたワイブル分布を学びます。
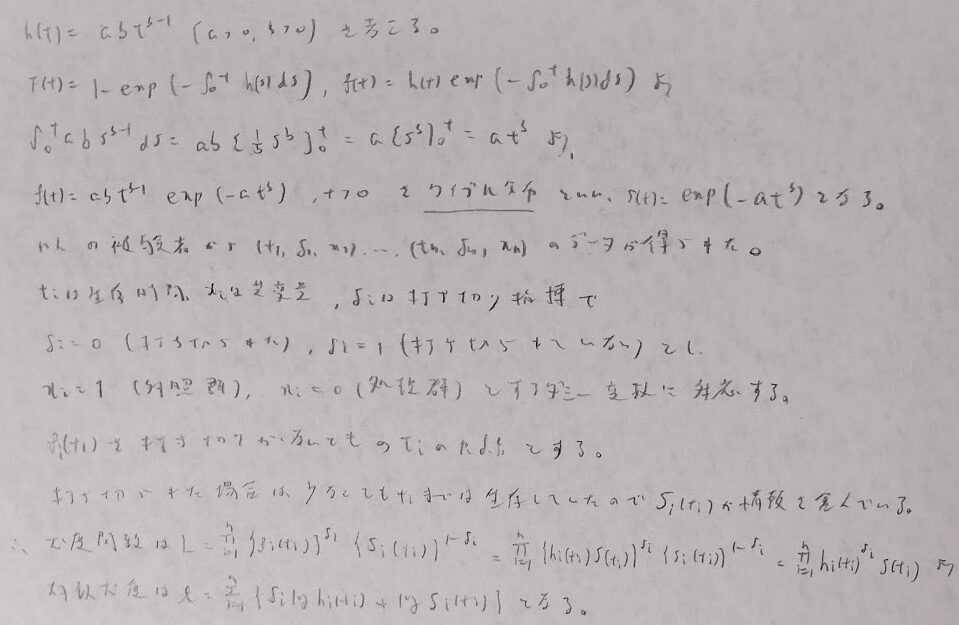
実際の解析法を学びます。
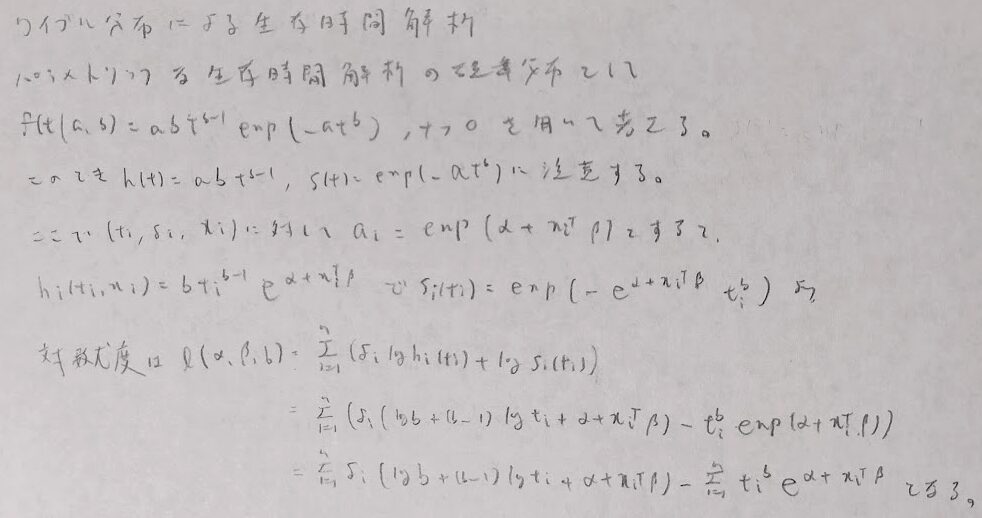
ワイブル分布による生存時間解析を一般化したコックスの比例ハザードモデルを学びます。
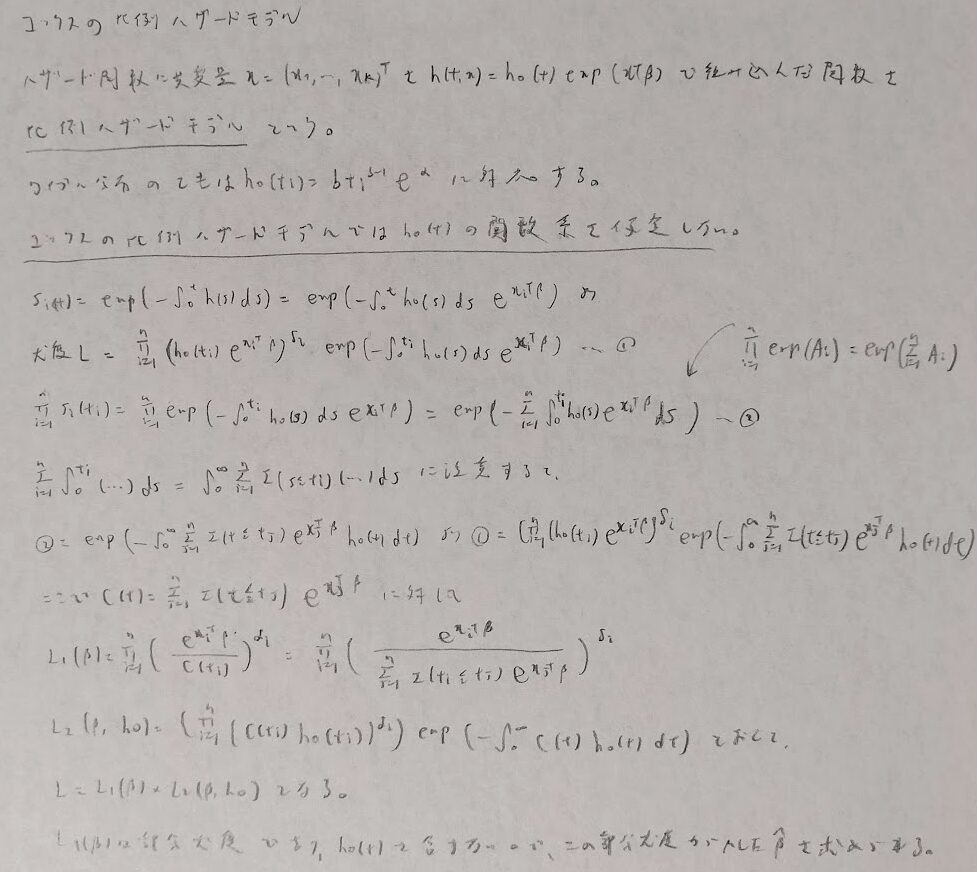
最後にカプラン・マイヤー推定量を用いて生存関数を推定します。

データ解析のための数理統計入門の第16章『分布によらない推測法』の演習問題
問1:分位点
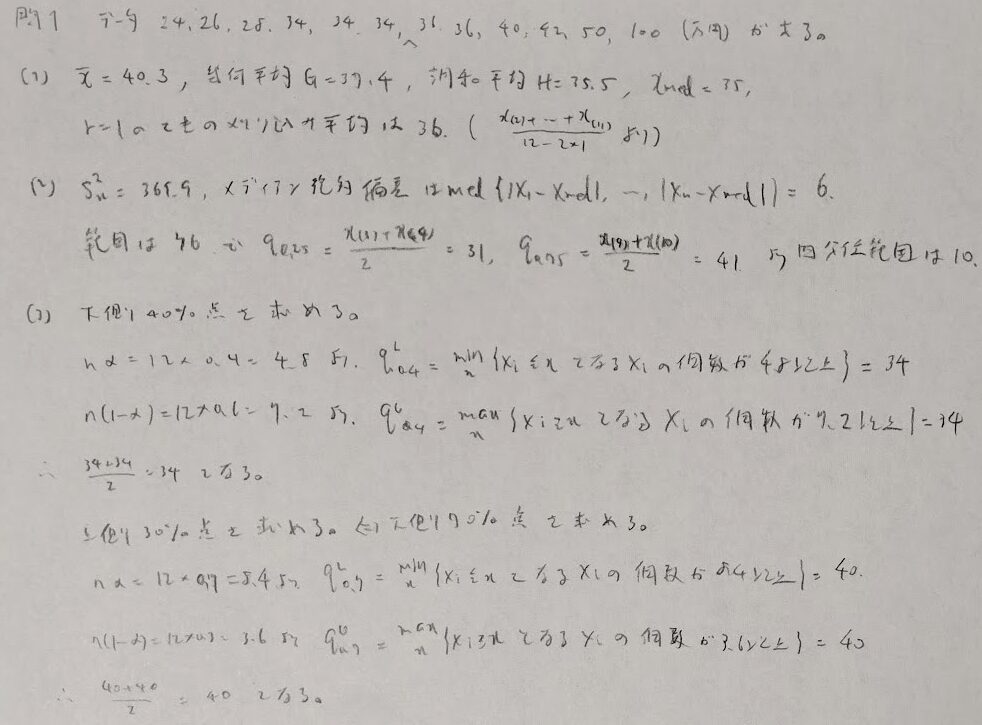
問2:標本相関係数

問3:ブートストラップ標本
問3と問4は計算のしようがないので模範解答を参考にしました。

問4:ブートストラップ標本

問5:符号検定とウィルコクソンの符号付き順位和検定

問6:ウィルコクソンの順位和検定
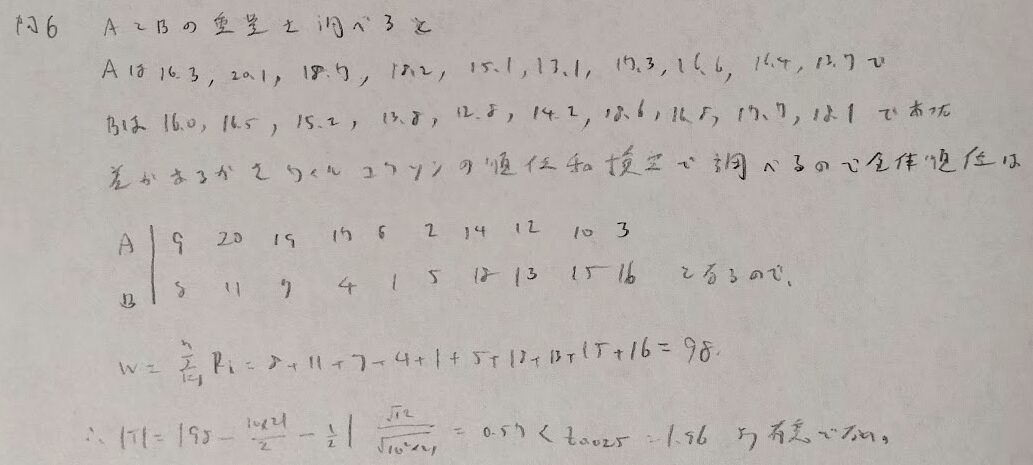
問7:クラスカル・ウォリス検定
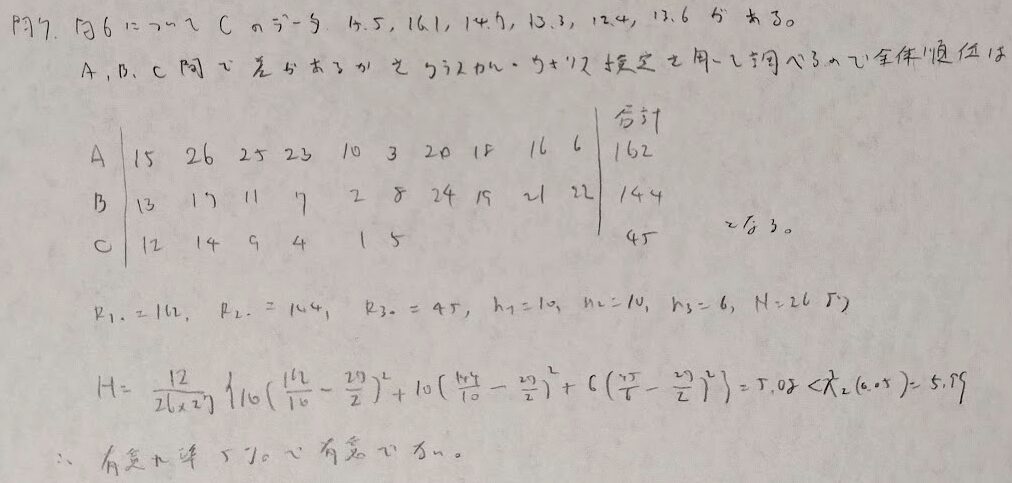
問8:連検定
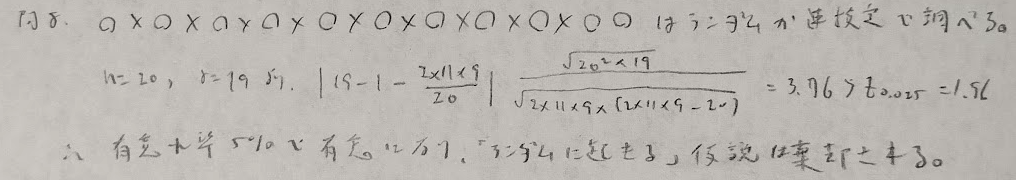
問9:ワイブル分布に従う乱数
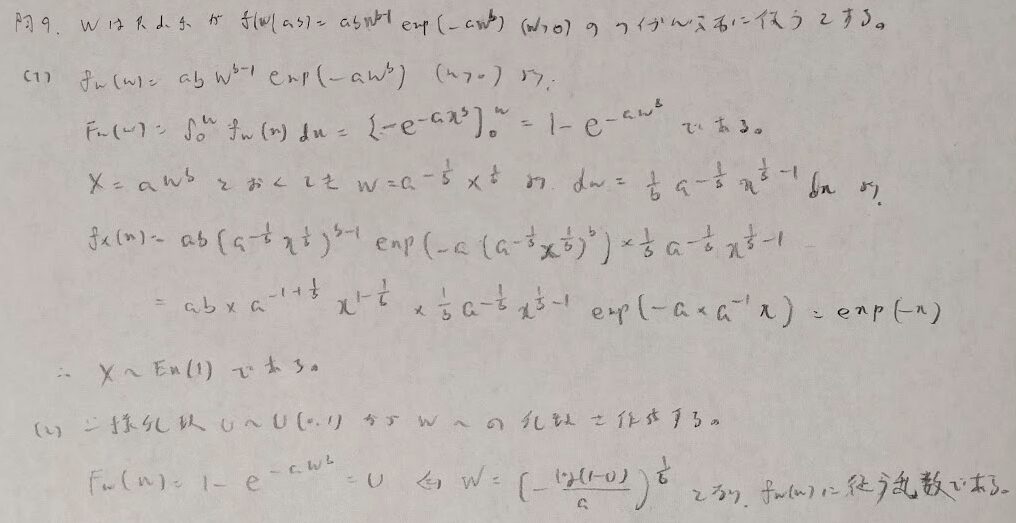
問10:平均余寿命関数
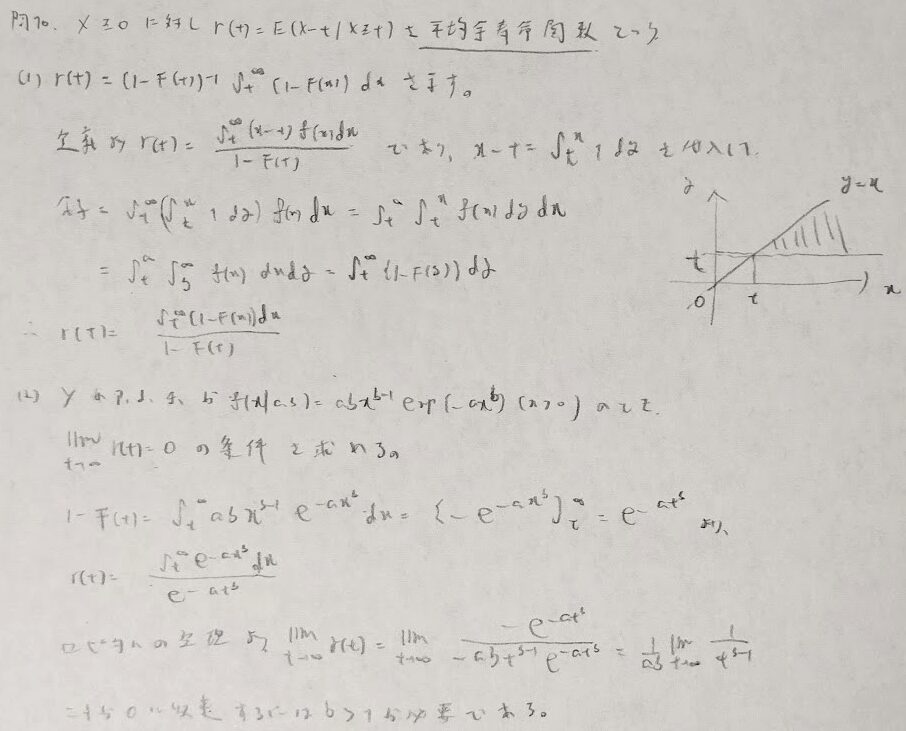
問11:ワイブル分布とQ-Qプロット
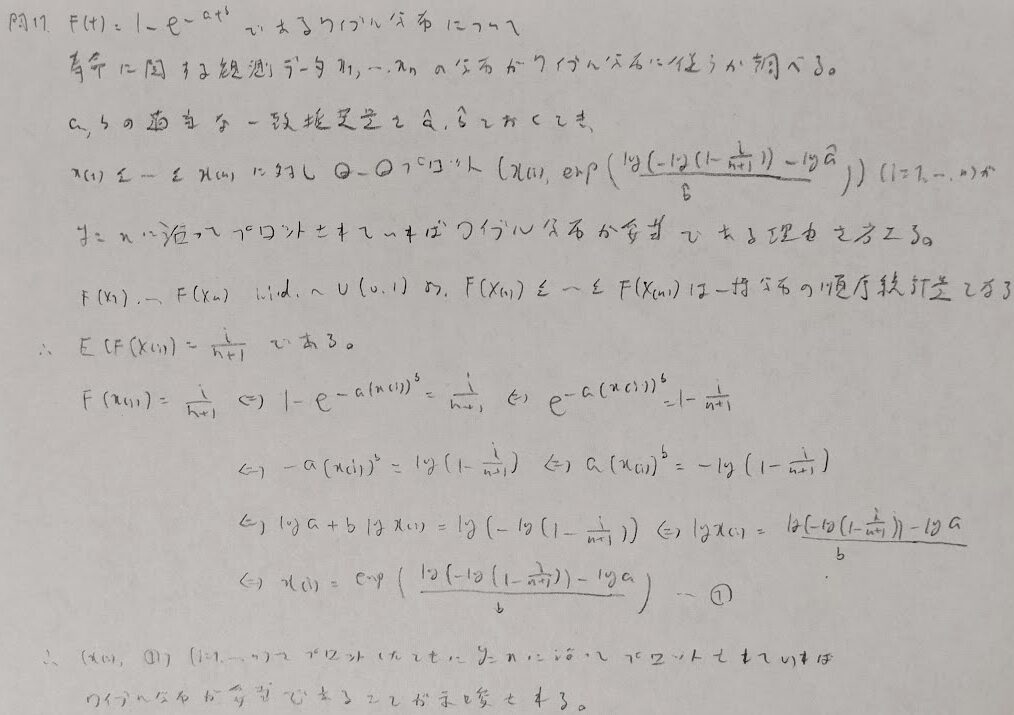
問12:カプラン・マイヤー推定値
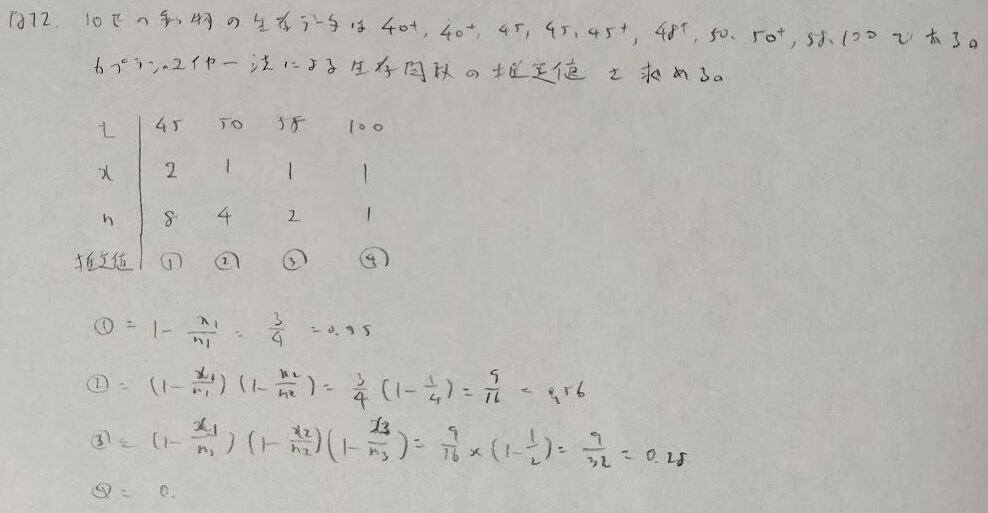
以上でノンパラメトリックの章は終了です。
とてもボリューミーでしたが、大事な内容がコンパクトにまとまっている印象でしたね。
そうですね。手法が多いので、何度も本記事を読み返して内容を消化したいところですね。




