アクチュアリー数学の有限母集団の過去問を扱います。この分野は期待値などの公式を覚えていれば乗り切れる問題が多いので、しっかりとクリアしたい分野です。本記事では有限母集団系の問題を完全に解き切れるように、体系立てて過去問を総整理し、学習効果を上げやすい順にまとめ直していますので、この記事の問題順に勉強すればOKです。
有限母集団単体では『確率統計演習 2 統計』にほぼ同じ問題が出題されています。アクチュアリー数学合格のためには必携の本です。アクチュアリー会からも公式の教材として提示されている名著です。
全体的なおすすめの公式集は『アクチュアリー試験 合格へのストラテジー 数学 第2版』です。お手元に置いて本記事をご覧くだされば学習効率が上がります。
標本平均主体の典型パターン(任意抽出法)
過去問を解くために次の公式の理解が必要です。
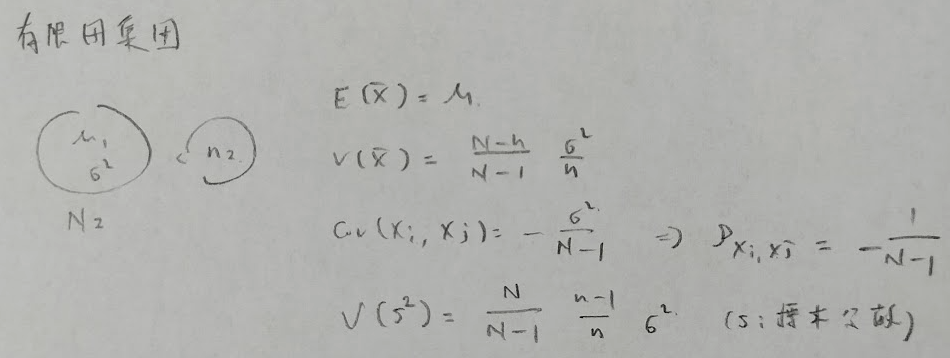
今後試験で狙われる可能性があるため証明をしておきます。

平成元年度問1(2)典型問題

非復元抽出であることが公式の発動条件です。
推定量の分散などを求めるパターン(任意抽出法)
平成7年度問1(3)推定量の分散
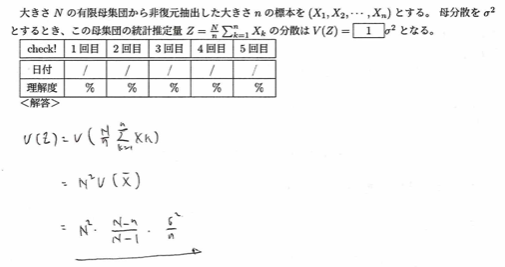
このようなパターンでは標本平均と推定量との間の関係を考えます。
母平均と母分散を求めるパターン(任意抽出法)
平成2年度問1(1)母分散を求める

この問題の母分散は、1〜13のカードから一様に1つを取り出す時の状況を考えればOKです。別解も追記します。
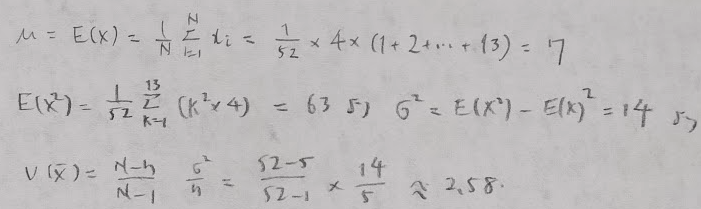
平成4年度問1(4)母平均も求める

対称性がない分だけ、前の問題よりも複雑な設定ですので別解も追記します。
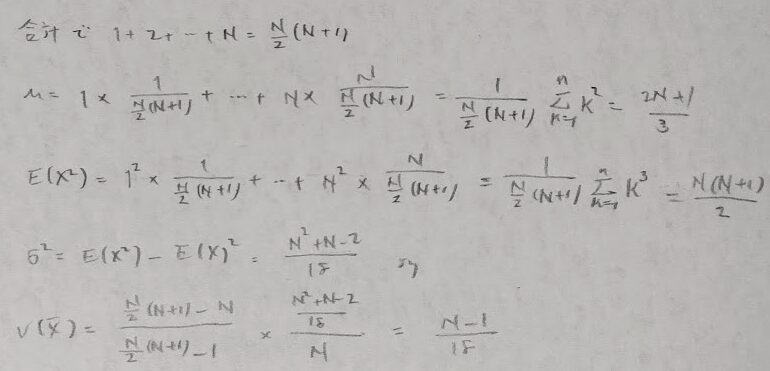
平成13年度問2(6)合計値

和の平均とは、和の期待値ということです。
平成19年度問1(7)新たな公式

相関係数は後述します。
相関係数を求めるパターン(任意抽出法)
平成5年度問1(2)相関係数

公式化するとマイナーな公式になります。しかし覚えておきたい問題です。今後出題の可能性が高いです。
抽出法のパターン(任意抽出法以外を含む)

またQC検定1級の範囲になってしまいますが、関連公式として2段抽出法の公式もあります。

無限母集団の場合は、MとNを無限にすればOKです。また、M=mの場合は層別サンプリングで、N=nの場合は集落サンプリングとなります。
平成9年度問1(6)層別抽出法

要素を文字で置いていくことがコツです。本問は公式の証明問題になっています。
平成29年度問1(8)比例抽出法

Nが無限大と見なせる場合、またはn/N < 0.05程度の場合、非復元抽出でも二項分布の考えを適用できるので分散計算で二項分布の分散の考えを用いています。
詳しい内容は下記の統計検定準1級の内容と同じです。
変動係数が絡むパターン
平成8年度問1(4)変動係数

総人口と総人口の推定量などを文字で設定するところから開始です。いつもの標本平均には総人口の推定量を用います。
有限母集団系の中の最難関が変動係数が絡む問題です。とにかくややこしい設定ですので、落ち着いて処理しましょう。有限母集団単体では『確率統計演習 2 統計』にほぼ同じ問題が出題されています。アクチュアリー数学合格のためには必携の本です。アクチュアリー会からも公式の教材として提示されている名著です。




-scaled.jpg)
