アクチュアリー数学の時系列解析の過去問を解説します。下記の本にはARMA(2,2)以外の公式は全て載っているので、まずはそれをしっかりと覚えましょう。その上で、定常性がない場合のAR(p)モデルが出た場合は定義に従って考えます。この分野での頻出問題はAR(2)モデルです。
全体的なおすすめの公式・問題集は『アクチュアリー試験 合格へのストラテジー 数学 第2版』です。お手元に置いて本記事をご覧くだされば学習効率が上がります。
時系列解析の内容は統計検定では1級の統計応用になるまで(準1級では少しはありますが)馴染みが薄いため、ここで学習を行った後で過去問に移ります。
確率過程の定常性

ARモデル

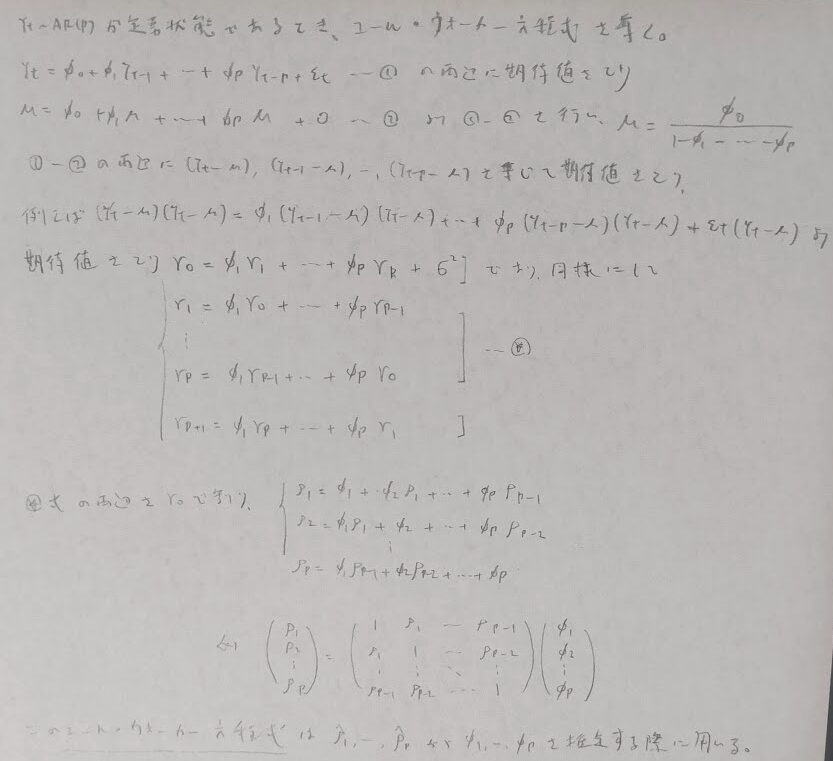
平成17年度問1(3)AR(1)モデル


定常状態ではない場合は、定義から求める必要があります。
平成29年度問1(11)AR(1)モデル

回帰分析との融合で計算量が多いため難易度が上がっています。
2024年度問4:長文問題


下から7行目の式で最後の1項目の前にφ1^h・Ynが入ります。すみません。加筆をお願いします。
平成18年度問1(10)AR(2)モデル
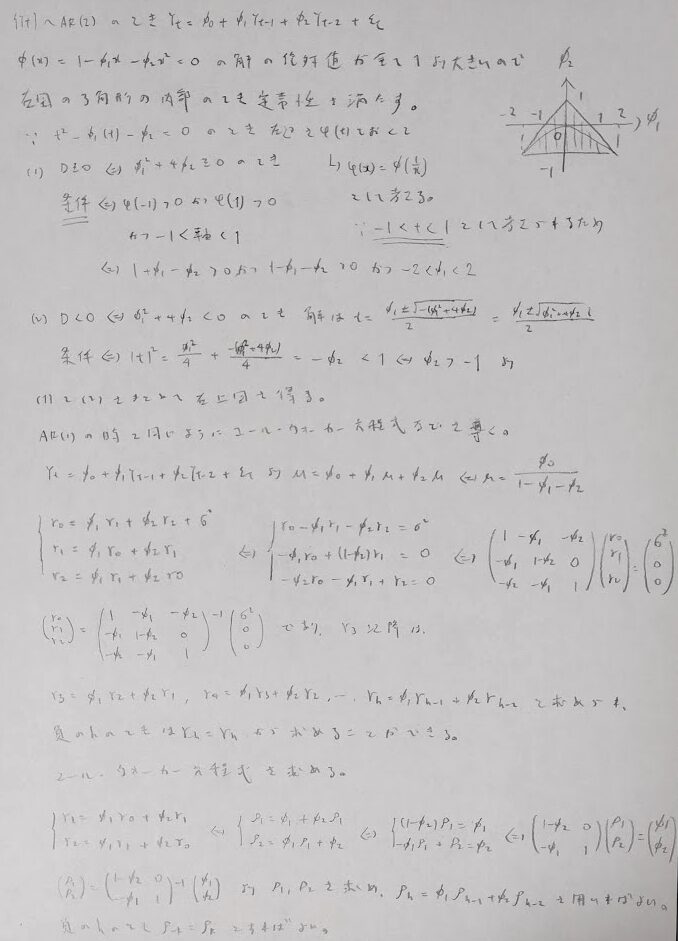

自己共分散の公式は必ず覚えましょう!
平成20年度問1(10)AR(2)モデル
三角形の領域は覚えておきましょう!
平成23年度問1(11)AR(2)モデル

ユールウォーカー方程式は必須です。この方程式はARモデルのみ存在します。ユールウォーカー方程式の派生形から偏自己相関を求めることができます。
平成27年度問1(11)AR(2)モデル

平成28年度問1(11)AR(2)モデル

典型問題ですが、そもそも定常性が満たされないと、いつもの公式が使えないので注意しましょう。
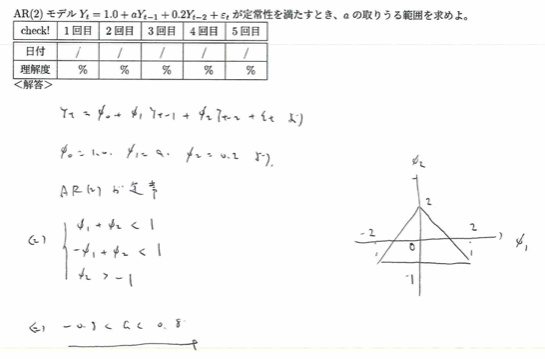
2023年度問2(6)AR(2)モデル

アクチュアリー数学の時系列解析の頻出問題はAR(2)モデルです。
MAモデル

平成19年度問1(10)MA(1)モデル

MA(p)モデルは反転可能性と識別可能性がありますので、ご注意ください。このモデルは必ず定常性を持ちます。
平成26年度問1(10)MA(1)モデル

識別可能の条件を見落とさないようにしましょう。またσ^2が未知なので、よく使える公式が使用不可であることにも注意しましょう。
平成25年度問1(11)MA(2)モデル

公式をしっかりと覚えましょう。試験中に0から導くのは誘導がない限りは悪手だと考えます。
2019年度問1(10)MA(2)モデル

AR(p)以外ではユール・ウォーカー方程式は使えません。ただし偏自己相関を求めるためのユールウォーカー方程式っぽいものは使えます。
平成22年度問1(10)MA(∞)モデル


この公式もしっかりと覚えましょう!知っていれば代入作業です。最後は漸化式を解くだけです。
通常の公式とは少しだけずれているので注意が必要です。不安の際は、実際にどんどん代入していって係数比較が安全です。
2020年度問1(10)MA(∞)モデル

以前の問題と異なるのは最後の問題の有無です。最後の問題は定数に気をつければ解けます。
ARMAモデル

2018年度問1(11)ARMA(1,1)モデル


アクチュアリー数学の時系列解析の中で最も覚えにくい公式です。この公式を覚えるくらいなら導出法をしっかりと学んで、時間をかけてでも確実に正答できる方が、続くARMA(2,1)モデルなどの問題にも落ち着いて対処できるようになります。
2021年度問2:ARMA(2,1)モデル

このタイプの公式はないので、素直に誘導に従って解いていくことになります。
まさかここまで出題されるなんて…と思った矢先に次の2022年度はさらなる難問が出ました。2022年度はアクチュアリー数学最難関です。
2022年度問2(5)ARMA(2,2)モデル

時系列解析の中で最難関です。途中の小問は時間内には解けません。
2022年度はバグだとしても、それ以外の問題を典型問題と言えるように、しっかりと下記の本で時系列解析の公式は覚えた上で試験に臨みたいですね!
下記の本の該当箇所を読んでいて気になったことがあったので追記します。2025年12月の試験直前の現在、出題歴はありませんが、同時分布を答えさせる問題がある場合は2変量正規分布の考えに従うとうまくいきます。
ARIMAモデル
アクチュアリー数学の過去問には2025年11月現在、出題歴はありませんが今後の出題が予想されるため、追記します。
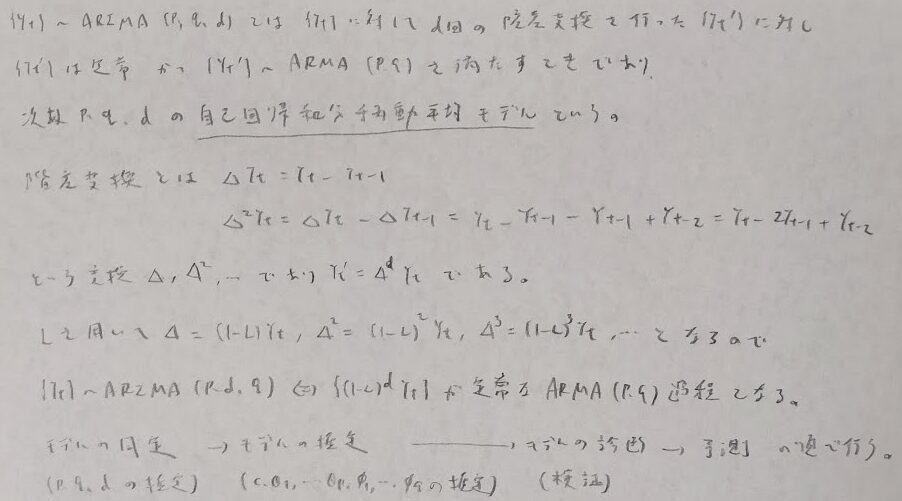
モデルの同定
モデルの同定では最初にdを決定します。dは時系列データや標本コレログラムを用いて決定します。定常な時系列では平均が一定となるので増加や減少のトレンドを含まないようにします。標本コレログラムでは定常状態の際は急速に0に収束することが重要です。これらが満たされるまでdを行います。
その後でARMA(p,q)の次数のpとqを決定します。この場合も標本コレログラムが有用になります。
AR(p):hが大きくなると指数関数的に0に収束
MA(q):h=q+1以降は突然0になる
ARMA(p,q):hが大きくなると指数関数的に0に収束
実はこの内容は統計検定準1級の範囲で対策記事でも類似問題に言及しています。
一方でpとqの推定については偏自己相関を用いる内容が試験では頻出です。
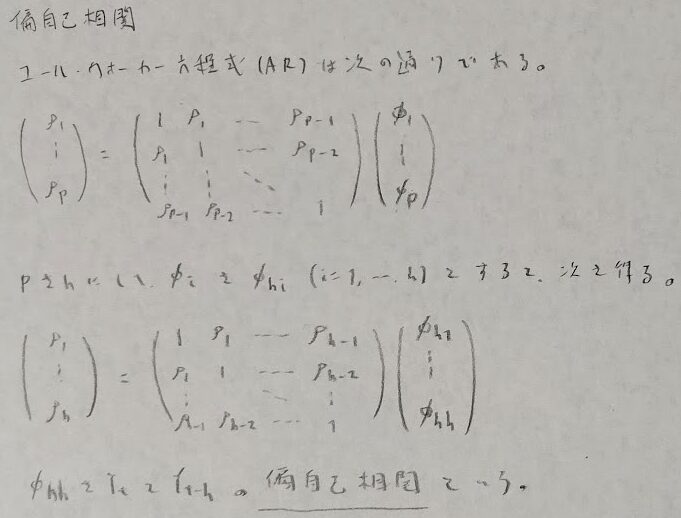
偏自己相関による各過程の様子は次の通りです。
AR(p):h=p+1以降は突然0になる
MA(q):hが大きくなると指数関数的に0に収束
ARMA(p,q):hが大きくなると指数関数的に0に収束
この偏自己相関による結論はコレログラムの判定と反対になっていますね!
AR(p):h=p+1以降は突然0になることはことはユール・ウォーカー方程式から導かれます。実際は試験問題で瞬時に0と書くことになります。
モデルの推定
次数pとqとdが決まったので、AR(p)、MA(q)、ARMA(p,q)に対してパラメータを推定することができます。
AR(p)の推定
最小二乗法と標本自己相関を用いる方法があります。
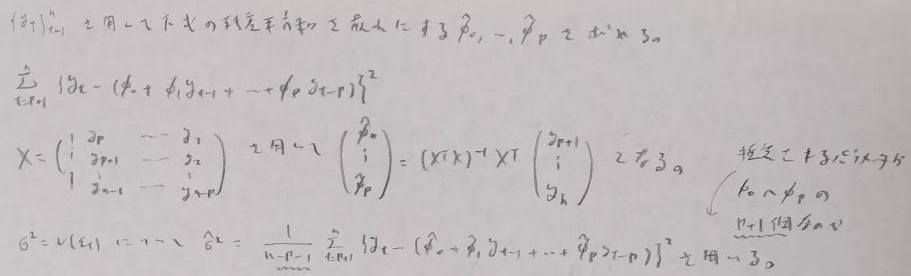
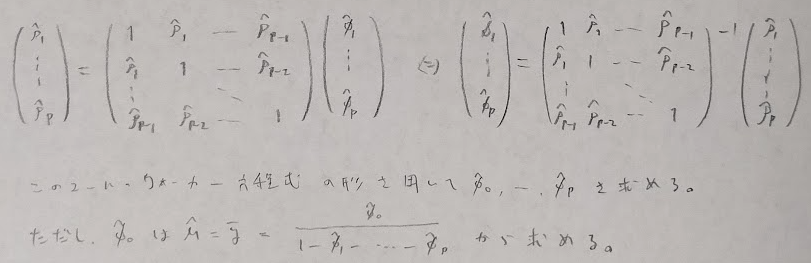
MA(q)の推定
最小二乗法と標本自己相関を用いる方法があります。

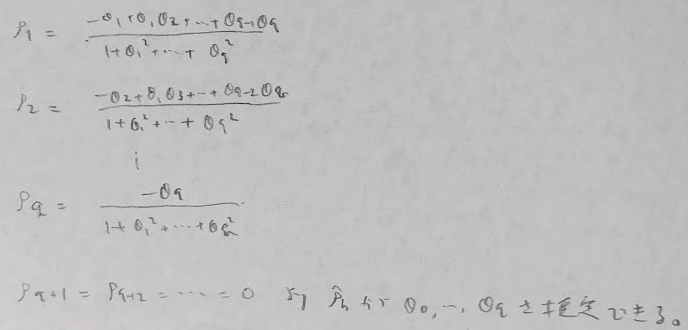
ARMA(p,q)の推定
こちらは最小二乗法を用いる方法があります。
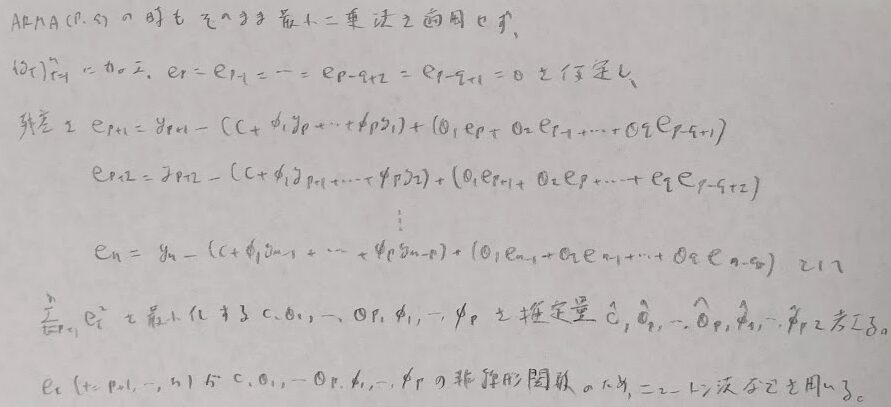
モデルの診断
まずは残差のプロットを行うことにより残差に特定のパターンがないかを確認できます。
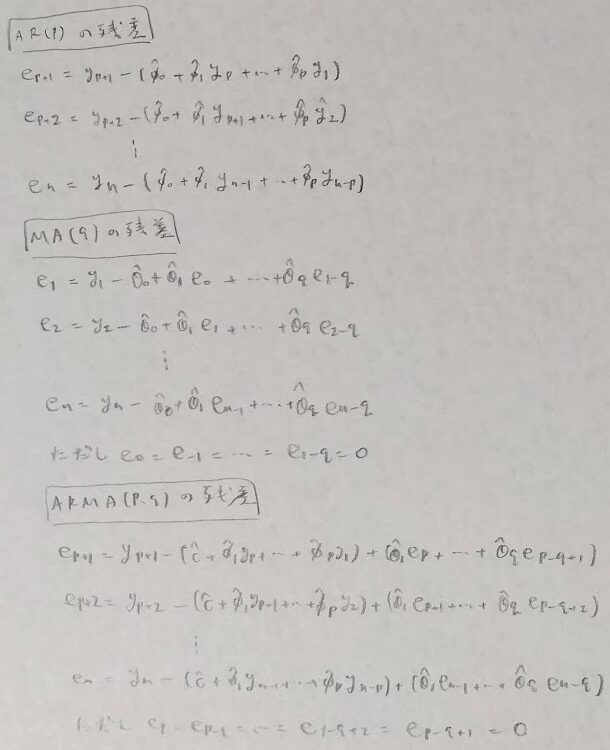
残差系列を用いてモデル診断のための統計量を計算し、その値によってモデルの妥当性を検定することができます。

またはAICによる判断もできます。
予測
予測量が下記の条件付き期待値で表現されることは平均2乗平均を最小にすることで証明ができます。
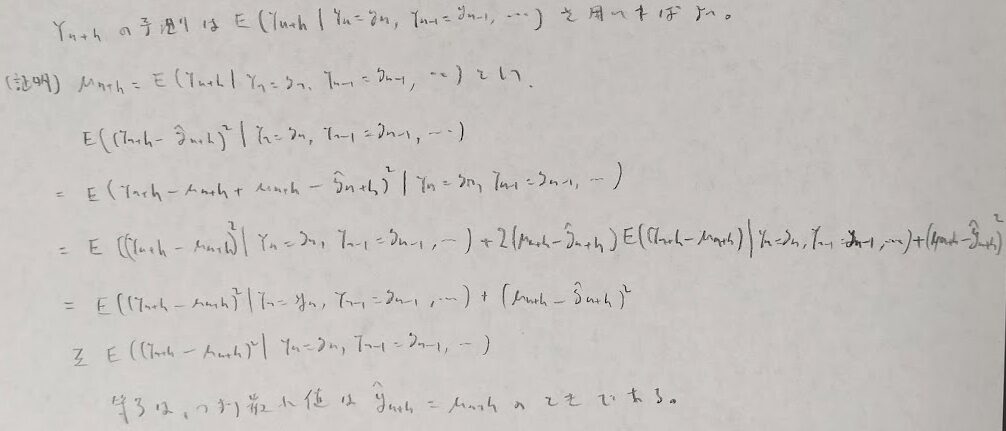
モデル別に見ていきますとAR(p)がやや複雑ですが、MA(q)は単純です。
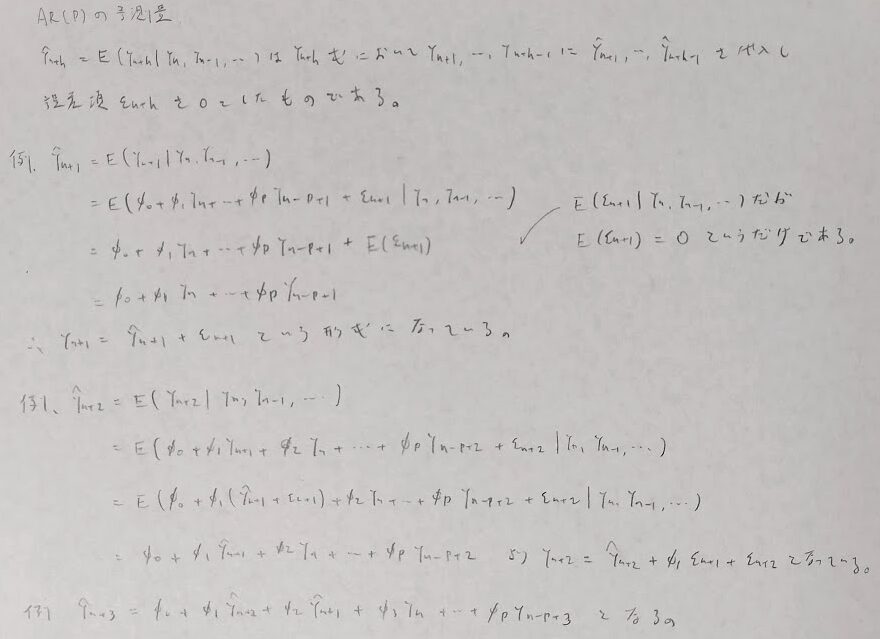

ARMA(p,q)は上の2つのモデルを組み合わせることで予測できます。
これは予想通りの結果ですね。

全体的なおすすめの公式・問題集は『アクチュアリー試験 合格へのストラテジー 数学 第2版』です。お手元に置いて本記事をご覧くだされば学習効率が上がります。



-scaled.jpg)
