確率過程の章ではマルコフ連鎖とブラウン運動(ウィーナー過程)とポアソン過程を扱います。マルコフ過程はマルコフ連鎖が離散的だとすれば、刻一刻と変わる連続量を扱うことになり、アクチュアリー数学ではマルコフ連鎖が出題されます。
この分野は前回の時系列解析よりも公式が少ないです。そのためしっかりと得点したいところです。
この分野は統計検定準1級と内容が被っています。下記と併用の学習をおすすめします。
全体的なおすすめの公式・問題集は『アクチュアリー試験 合格へのストラテジー 数学 第2版』です。お手元に置いて本記事をご覧くだされば学習効率が上がります。
マルコフ連鎖
マルコフ性とは将来のある時点の得点は、現在の得点のみに依存し、過去の得点の推移には依存していないということです。
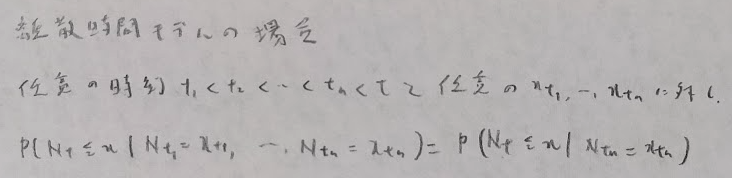
後のブラウン運動やポアソン過程はマルコフ過程です。他には誤差項がホワイトノイズ(期待値0、分散一定、自己相関0)の時のAR(1)モデル、ランダムウォークなどです。後述しますが加法過程もマルコフ過程です。
AR(2)モデルは2重マルコフ過程です。
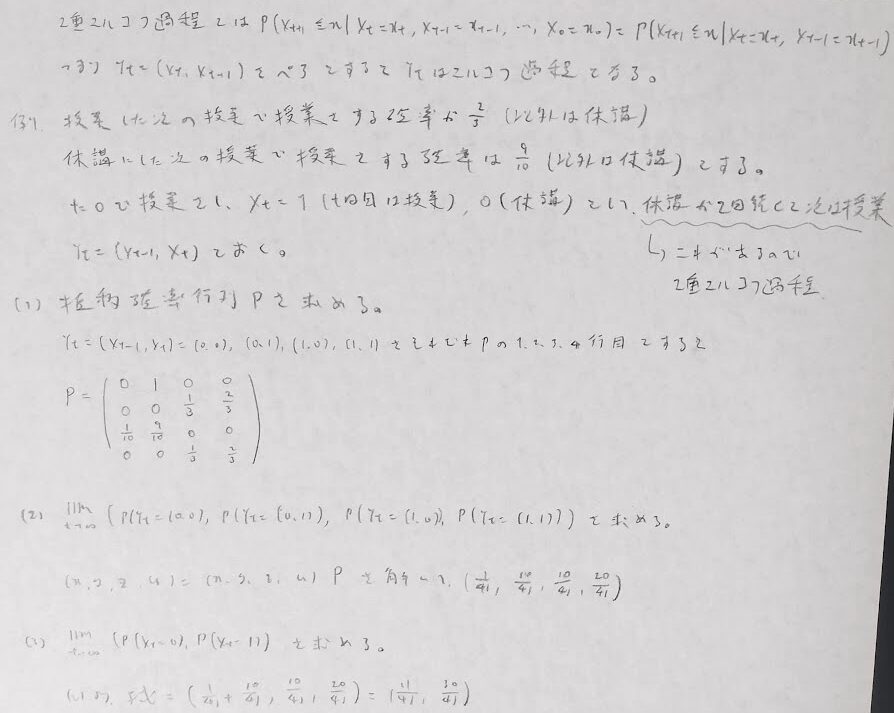
また似た概念にマルチンゲールがあります。これは期待値で定義されます。
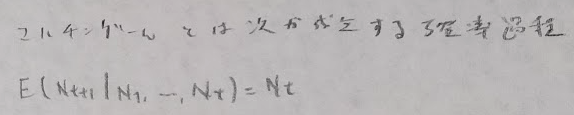
有名な定理を証明しておきます。
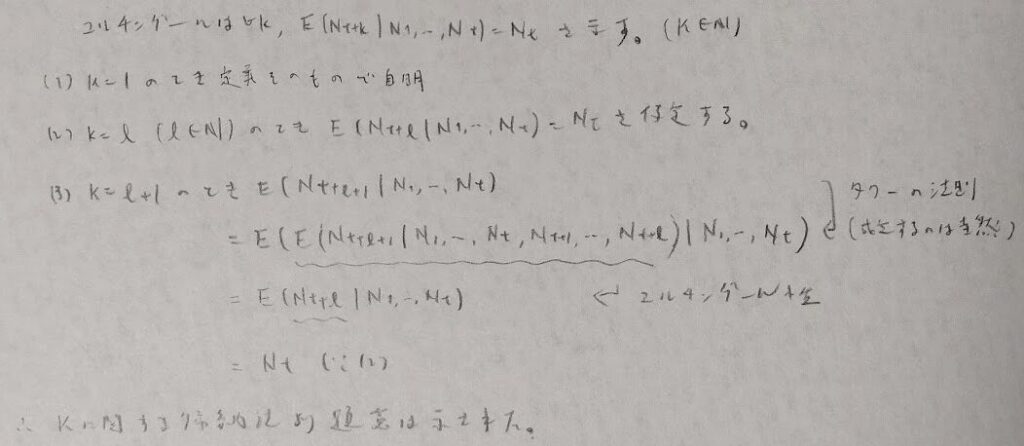
アクチュアリー数学の頻出分野である推移確率行列をここで定義します。
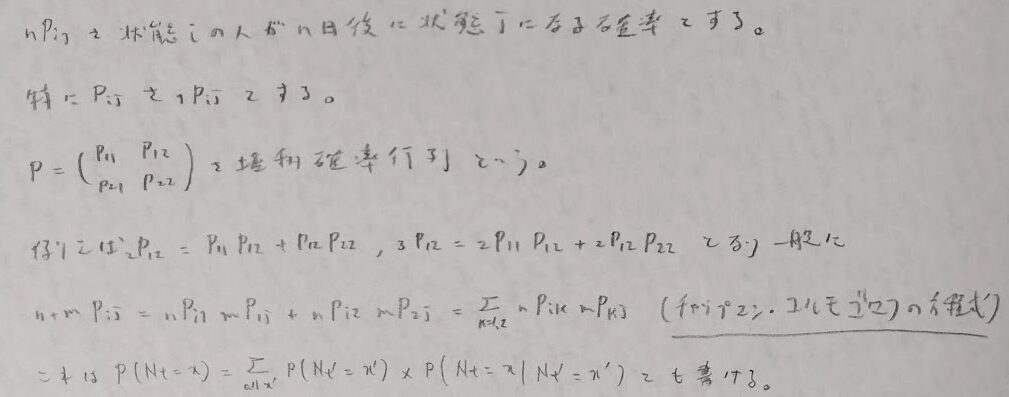
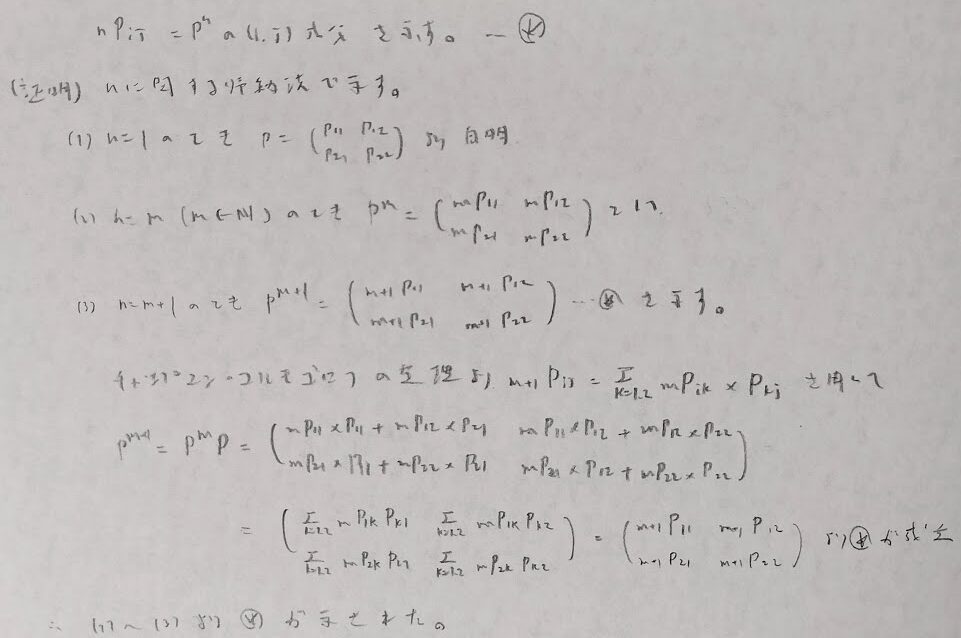
また定常状態を求める問題では構成要素に注目するとスピーディーに出すことができます。
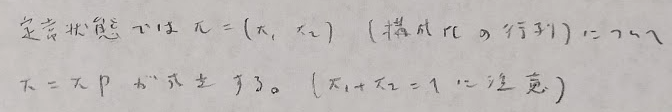
昭和63年度数学Ⅰ問1(5)天候

かなりシンプルな問題です。
平成元年度数学Ⅰ問1(4)推移確率

まずは推移確率を作ってしまいましょう。その上で何を求めれば良いのか?を考えます。
平成11年度数学Ⅰ問1(4)停止パターン

平成17年度問1(7)出勤問題

推移状態の設定が難しい良問です。
平成18年度問1(9)格付け問題

平成19年度問1(11)定常分布

平成21年度問1(11)ブロック行列

平成23年度問1(12)会員問題

面白い設定です。落ち着いて順に計算していきましょう。
平成24年度問1(11)推移行列の見方

平成29年度問1(10)学年推移

かなり複雑な設定です。落ちついて処理しましょう。
2020年度問1(11)四面体

2023年度問3:推移確率


昭和63年度問5のマルコフ連鎖の問題が全くわかりません。アクチュアリー数学で最も難しい問題です。
確率過程の追加問題『弱点克服 大学生の確率・統計』より
『弱点克服 大学生の確率・統計』を用いた演習問題を解いてみましょう。
まずは対称型の簡単な例題です。
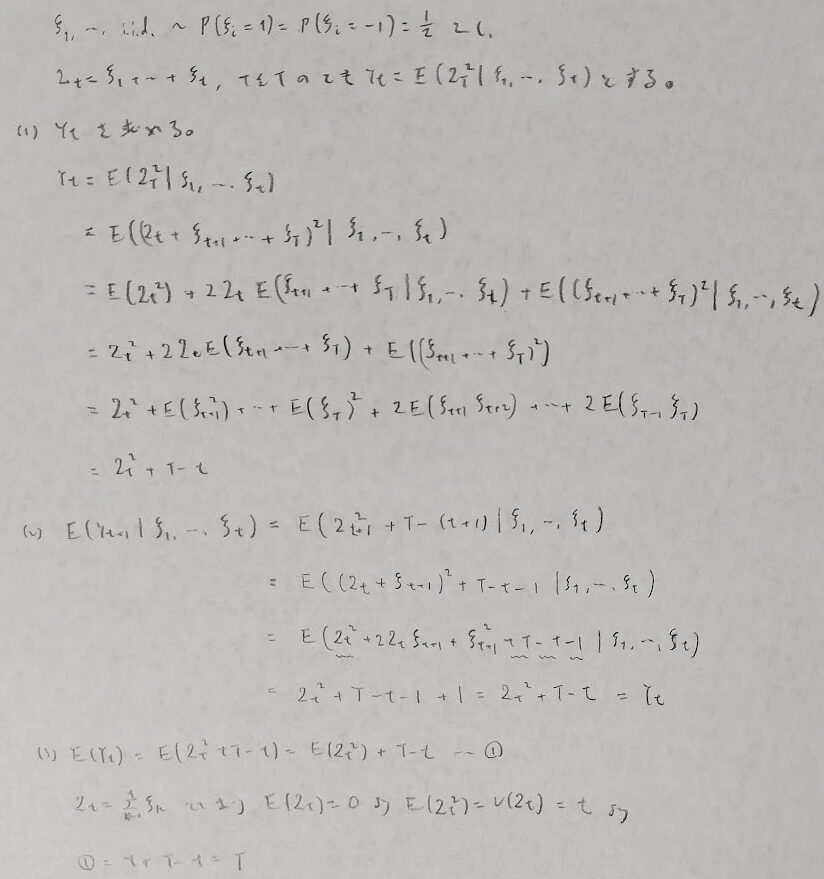
本格的に対称ランダムウォークと非対称ランダムウォークの問題を扱います。前者の期待値は0です。非対称の特別な場合が対称となります。

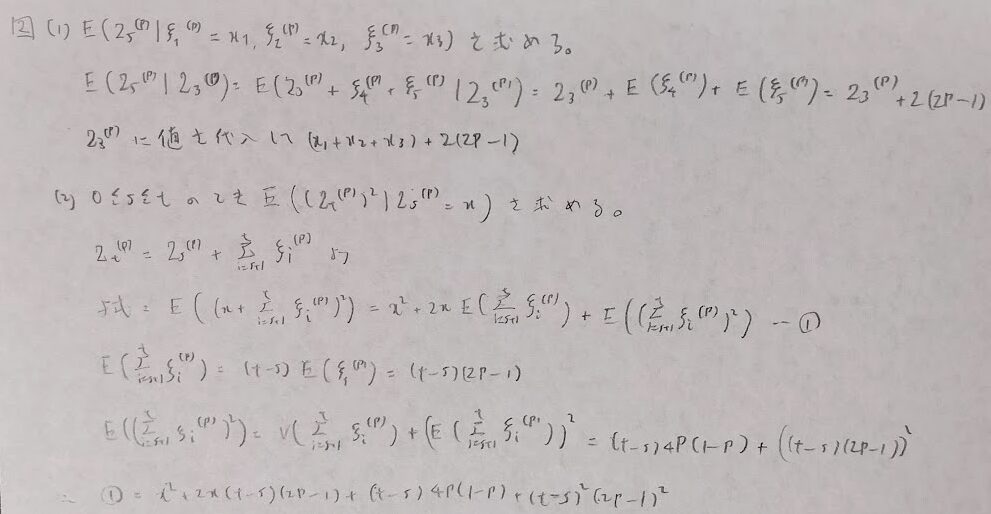
さらに難易度の上がった問題も見ていきましょう。
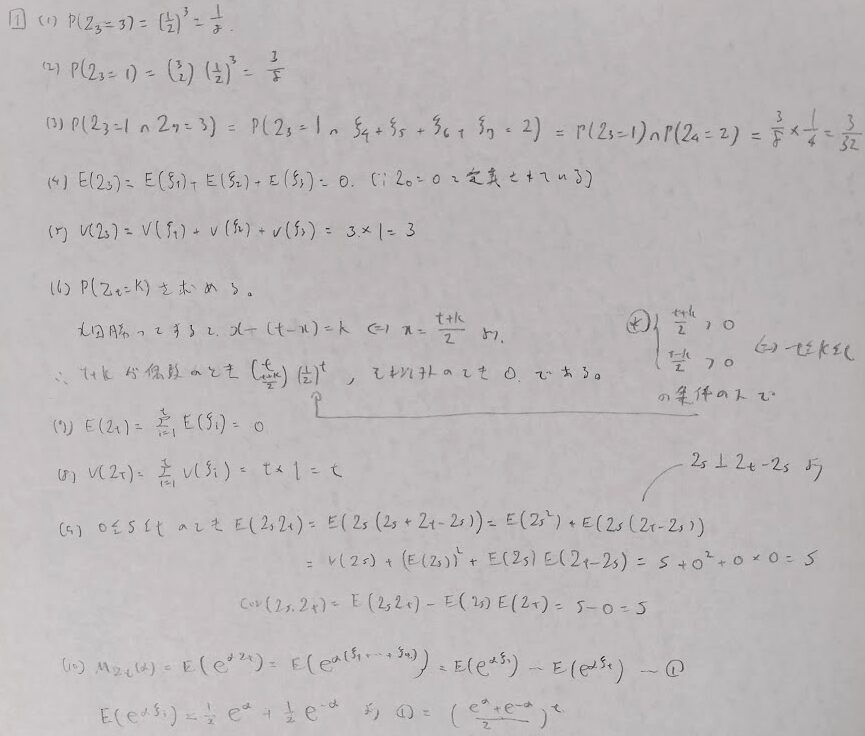
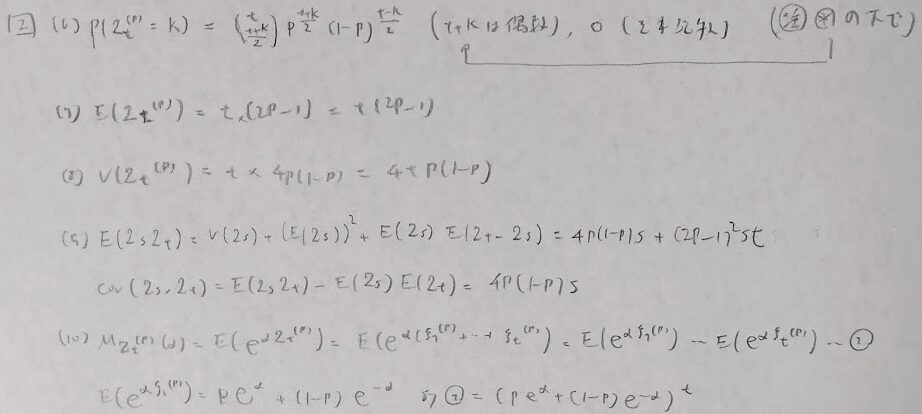
ポアソン過程
確率過程の章では最も頻度が低い分布です。だからこそ狙われる可能性があります。後述するウィーナー過程よりも分散のところがやや複雑になります。まずは計数過程を定義します。

計数過程の特別な場合がポアソン過程です。
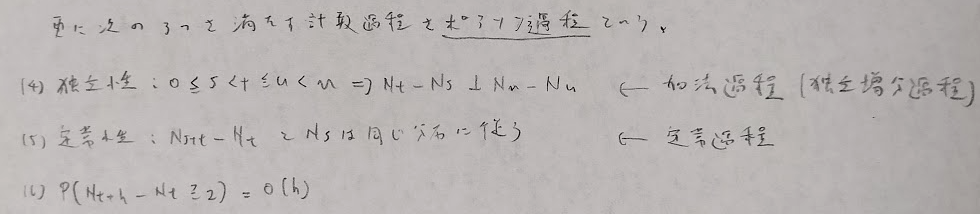
ポアソン過程については次の内容が有名です。
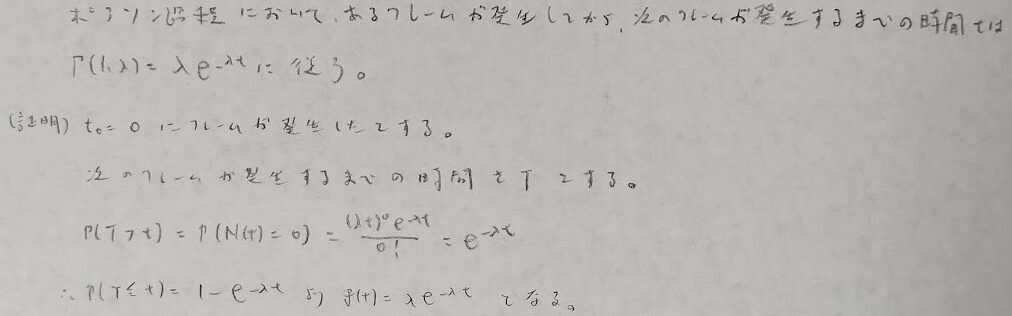
上の証明ではNtが従う分布がポアソン分布であるという事実を用いています。そのためNtが従う分布を求めておきます。すなわち指数分布とポアソン分布で、どちらが既知の場合の証明か?というわけです。
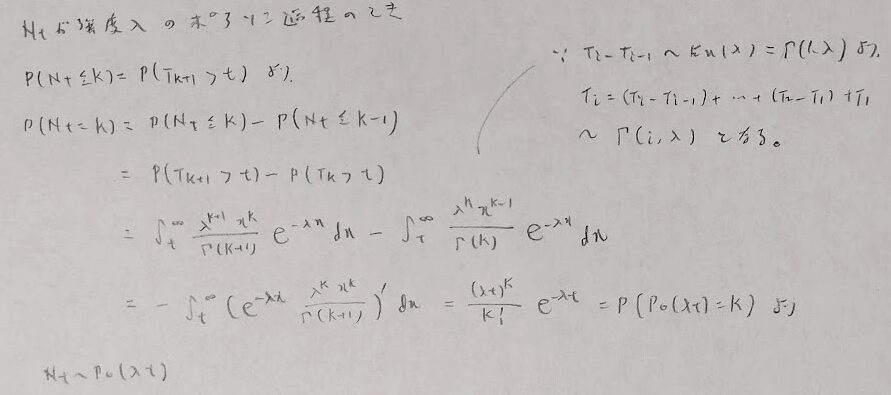
あるクレームが発生してから次のクレームが発生するまでの間の時間が同じ確率分布に従う確率過程を、再生過程といいます。すなわちポアソン過程は再生過程になります。
2019年度問1(11)増分性

この結果は覚えておいても良さそうですね。もちろん余裕があればです。
2022年度問2(6)条件付き期待値

ポアソン過程の最難関問題です。落ち着いて処理したい問題です。
ポアソン過程の追加問題『弱点克服 大学生の確率・統計』より
アクチュアリー数学のポアソン過程の問題量が乏しいため、『弱点克服 大学生の確率・統計』を用いた演習問題を解いてみましょう。

ブラウン運動(ウィーナー過程)
ブラウン運動はマルコフ連鎖から考えることができます。

このマルコフ連鎖nのnを無限にするときブラウン運動という確率過程となります。

ブラウン運動の特別な場合がウィーナー過程です。

ブラウン運動(加法過程の一種)はガウス過程と呼ばれ、標準ブラウン運動はウィーナー過程とも呼ばれます。
ほとんどがウィーナー過程の問題で次の公式を用います。
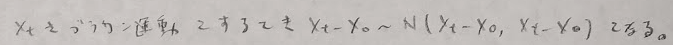
平成17年度問1(11)標準ブラウン運動
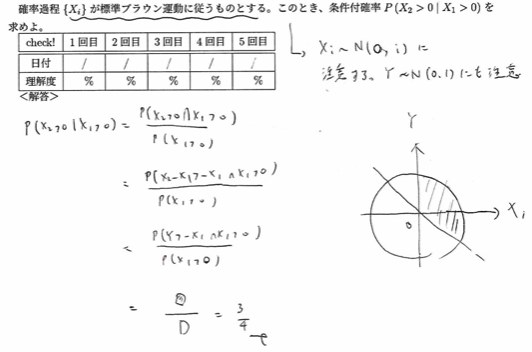
かなりテクニカルな問題です。両座標軸は同じ確率分布に従う(この分布は標準正規分布です)ので面積の考えが使えます。しかしこの解き方では応用問題が解けなくなる可能性が高いです。そのため正攻法でも解いておきます。
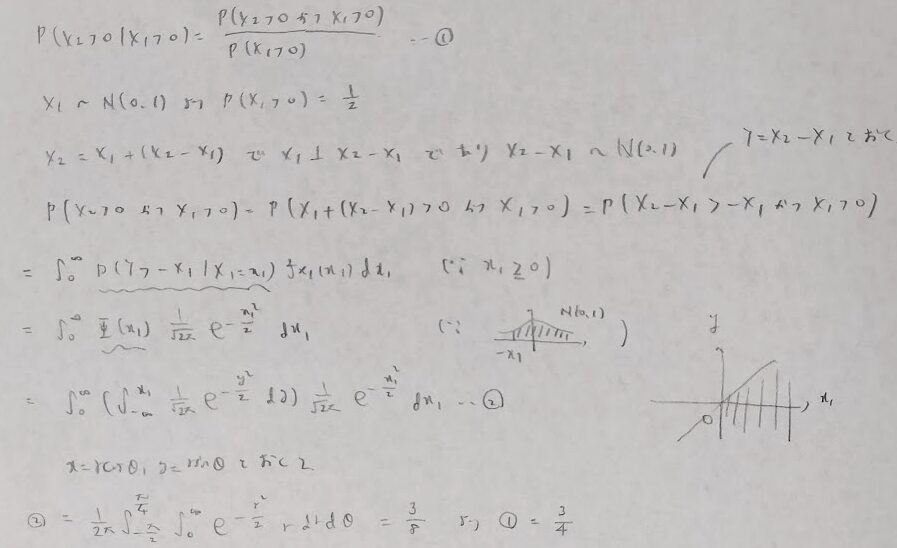
2024年度問3(2)標準ブラウン運動

平成20年度問1(11)増分性

平成22年度問1(11)重積分

平成28年度問1(10)変化球

2018年度問1(10)積率

2021年度問1(11)階段型

ブラウン運動の中で最難関です。困ったら標準正規分布に従う確率変数をつくっていくことを考えましょう。
ブラウン運動の追加問題『弱点克服 大学生の確率・統計』より
アクチュアリー数学のブラウン運動の補強として『弱点克服 大学生の確率・統計』を用いた演習問題を解いてみましょう。

全体的なおすすめの公式・問題集は『アクチュアリー試験 合格へのストラテジー 数学 第2版』です。お手元に置いて本記事をご覧くだされば学習効率が上がります。

-scaled.jpg)


