統計検定1級の対策書として公式本以外で真っ先に買うべき本である『データ解析のための数理統計入門』の第10章の解説と演習問題を自力で解いた学習の軌跡の記事です。本章は統計応用の共通問題に頻出のカイ2乗適合度検定に関する内容となります。特に演習問題は感動する問題が複数あります。
統計検定1級青本の第10章の説明と例題
本記事ではカイ2乗適合度検定の理論を学んだ後に、正規性の検定、指数分布における斉次性の検定、ポアソン分布の過分散検定まで扱います。
カイ2乗適合度検定
適合度検定は必ず片側検定になります。
まずはカイ2乗適合度検定の概要から解説します。多項分布に従って作られる表のデータから統計量を作り近似的にカイ2乗分布に従うことから検定を行います。
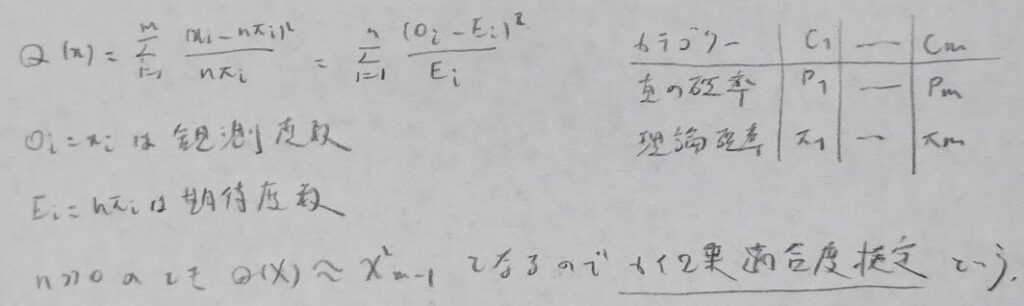
式の覚え方は分母にどっしりしたEがあると覚えます。
具体例としては血液型の調査の問題や著作が同一人物のものか?など幅広い問題を解決できます。


次は独立性に関するカイ2乗適合度検定について学びます。大きくカイ2乗適合度検定の中の1つの例としてとらえて欲しいです。最尤推定値からスタートすることがポイントです。

独立性の検定において、棄却の判定が微妙な場合があります。その際にフィッシャーの正確性検定が用いられます。

フィッシャーの正確性検定では超幾何分布を考えることになります。ここでxの範囲ですが、本書『データ解析のための数理統計入門』含めほとんどの書籍で考え方が端折られていたので、考え方をまとめてみました。
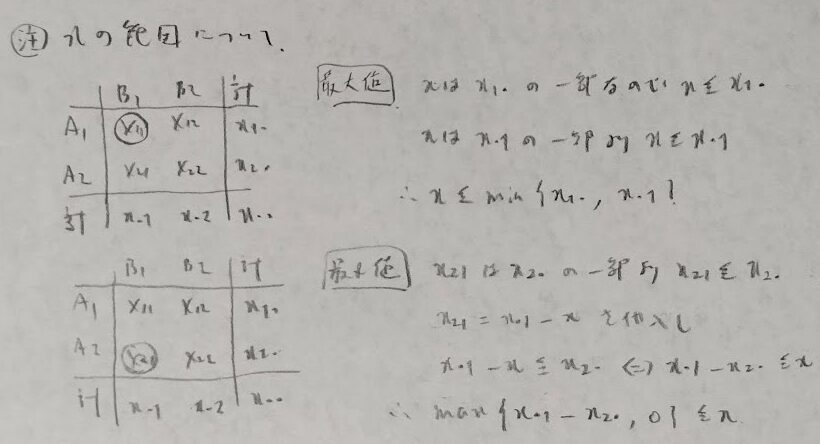
適合度検定とカイ2乗検定との間の関係式を本章では約束事の上で使用してきました。今回はその関係性を導いてみます。
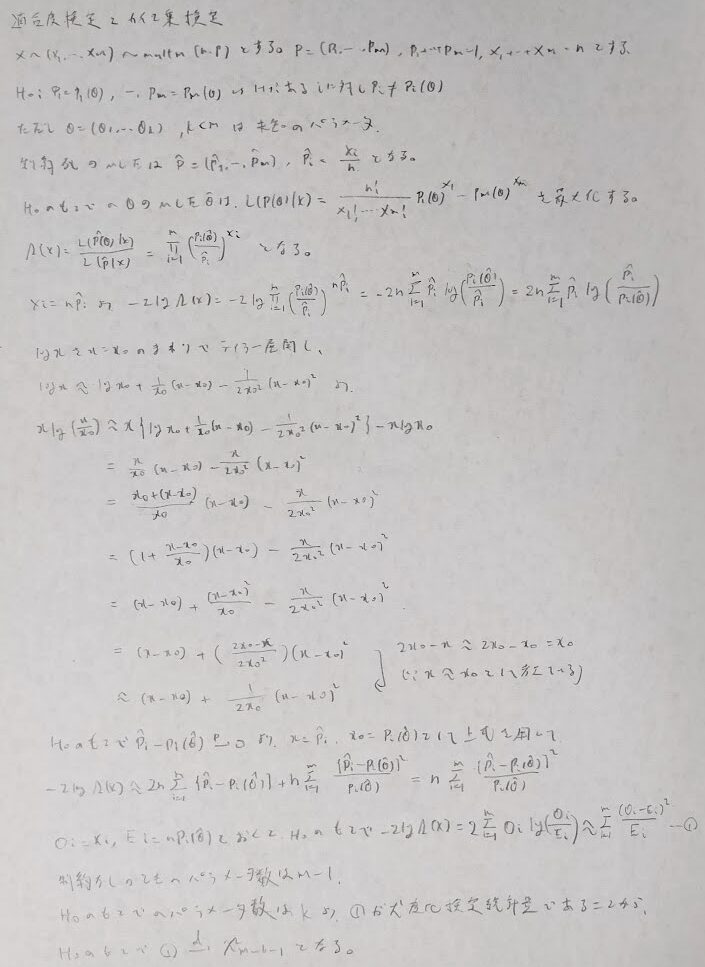
上述の答案で中盤の式変形が『データ解析のための数理統計入門』で端折られていたため、行間を埋めておきました。
分布系の検定
多くの分布に使えるP-PプロットやQ-Qプロットについて考えます。
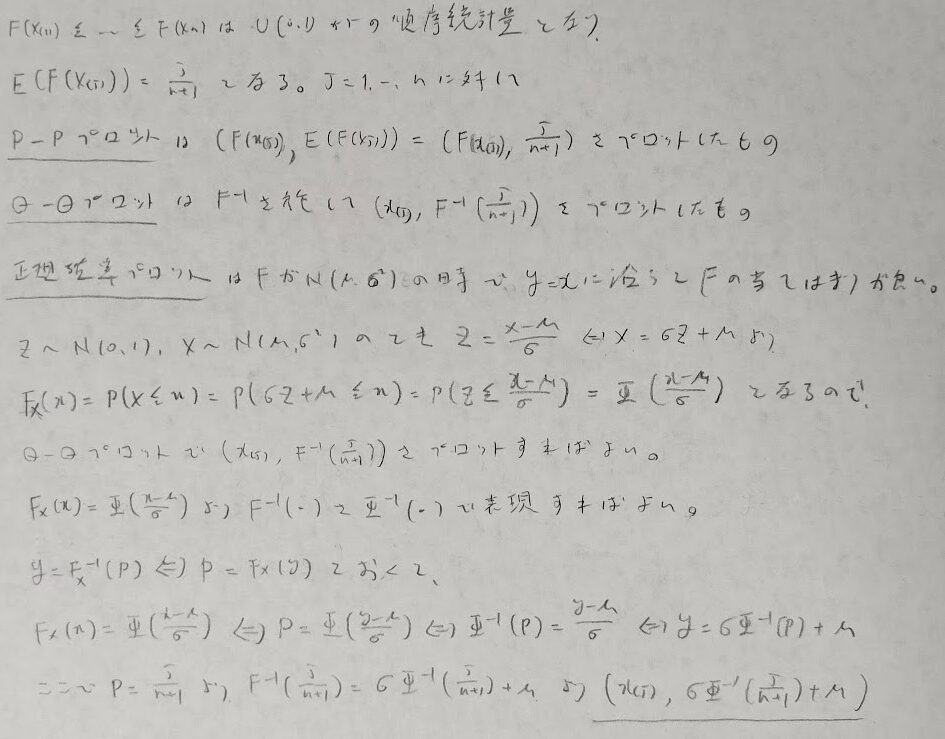
実際に正規性の検定を考えます。こちらもカイ2乗適合度検定を用います。ただしパラメータの自由度に注意です。
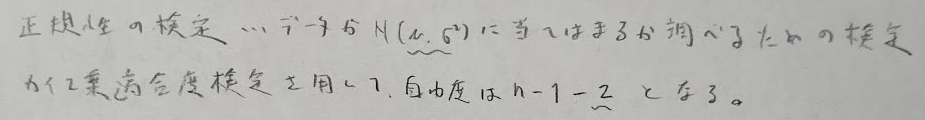
歪度(正だと右に裾の長いグラフ)と尖度も標本歪度と標本尖度があります。こちらはモーメント推定量から考えれば式の結果に納得がいきますね。
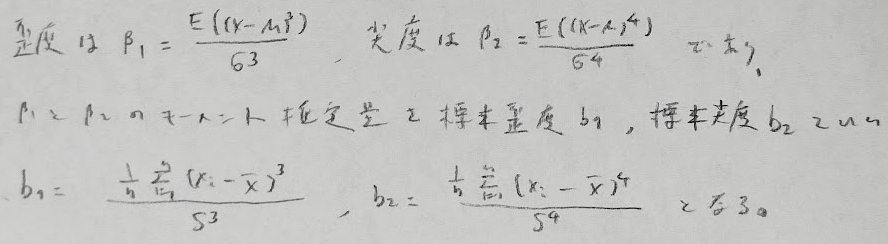
次に指数分布とポアソン分布に関する検定を学習します。ともにn個の確率変数が同一パラメータを持つ指数分布やポアソン分布に従うか?を考える問題です。前者を斉次的か否かの検定、後者を過分散検定などと言います。
指数分布とポアソン分布について未学習の方は下記の記事をお読みください。
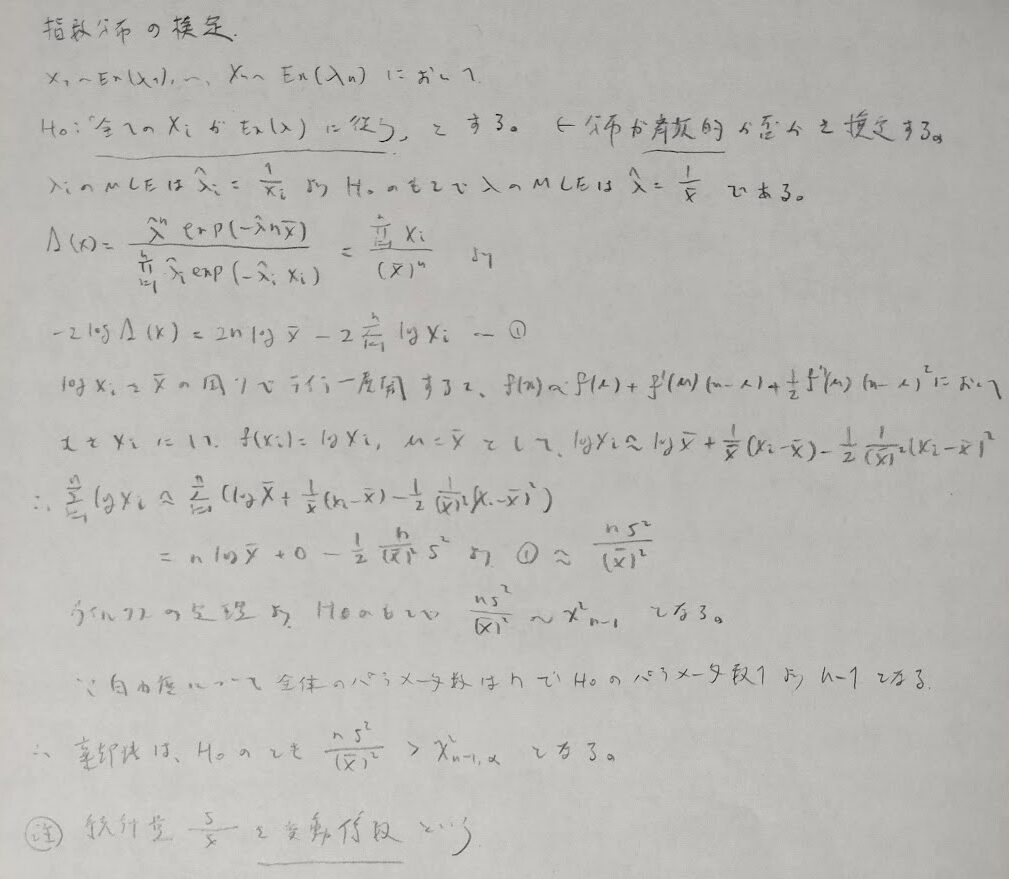
変動係数が出てくるところが感動的です。
次のポアソン分布に関する検定の結果も似たような感じになります。ポアソン分布における過分散とはn個の異なるパラメータを持つポアソン分布からのn個の確率変数において不偏分散の期待値が標本平均の期待値より常に上回ってしまう現象です。そこで過分散を起こす条件を考えていきます。

それではポアソン分布の過分散検定について詳しく追っていきます。
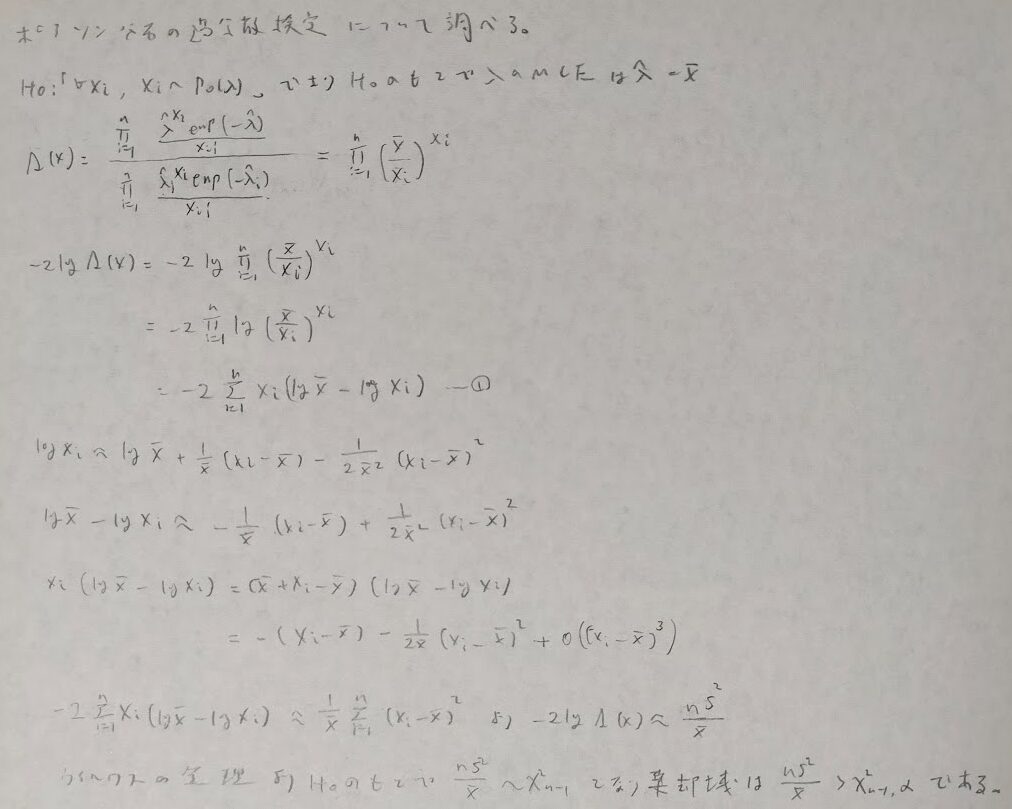
統計検定1級青本の第10章の演習問題
問1:一様乱数の検定
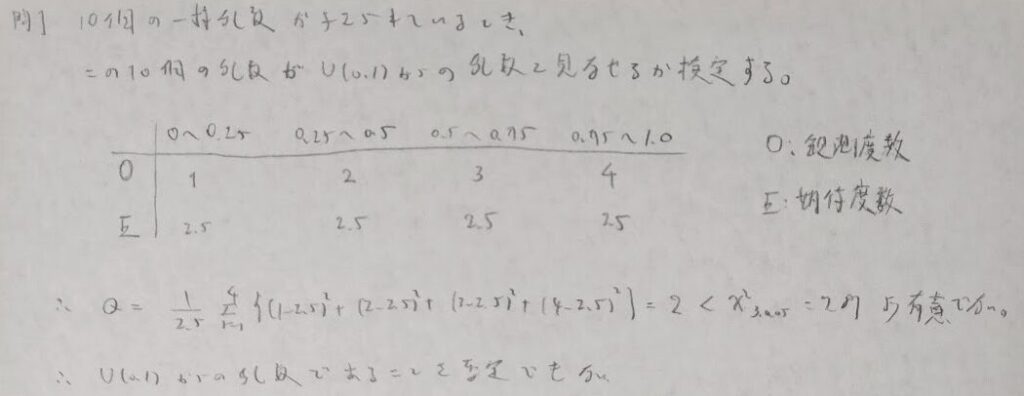
とても面白い問題ですが解き方を知らないテゴリー分けを行うことがポイントです。
今回の問題で0.1刻みなどで考えてしまうと、期待度数の条件(すべての期待度数が1以上、期待度数の80%が5以上)を満たせなくなりますのでNGです。このようにデータ数が少ない場合にはコルモゴロフ-スミノロフ検定(KS検定)が奨励されます。
問2:正規乱数の検定

問1とほぼ同じですが。理論確率を求める際に計算が必要です。
問3:メンデルの法則

P値が1になるとは、偶然に表のようになる可能性がほぼ100%ということは、データが出来過ぎなんじゃないのか?と疑う流れです。
問4:季節性の有無

ある事柄が起きた回数が観測度数と考えています。
問5:ハーディー・ワインベルグ平衡

難しそうな名前ですが、多項分布から出発しパラメータの最尤推定値を求めて、それらを用いて理論確率を出して、カイ2乗適合度検定に帰着させます。