カイ2乗分布を終えたので次はt分布へと進むつもりでしたが、このtweetのように考えてt分布へと進む前にベータ分布を先に学ぶ方が良いと思いました!
確かに!一般的な参考書ではカイ2乗分布の次はt分布へと進みますけど統計検定1級の受験者に1番人気の『現代数理統計学の基礎』などの参考書ではカイ2乗分布はt分布よりずっと前で解説されていますからね。何か意図があるのではないかと思いました。
カイ2乗分布で登場した標本分布の考えは、ベータ分布を1から解説するこの記事でも使用しますので、未読の方はご覧くだされば嬉しいです。
本記事では次のことを一緒に学んでいきます!まずは目次をご覧ください。
多項分布は二項分布の一般形だけでなく順序統計量の理解の基盤です
多項分布の確率関数
多項定理を学ぶ前に、二項定理を復習した方が良いです!
ではこれからベータ分布の本質的な意味である順序統計量を分かりやすく扱うために多項分布を勉強します。
二項分布が二項定理から導かれたように多項分布は多項定理から導かれそうですね!
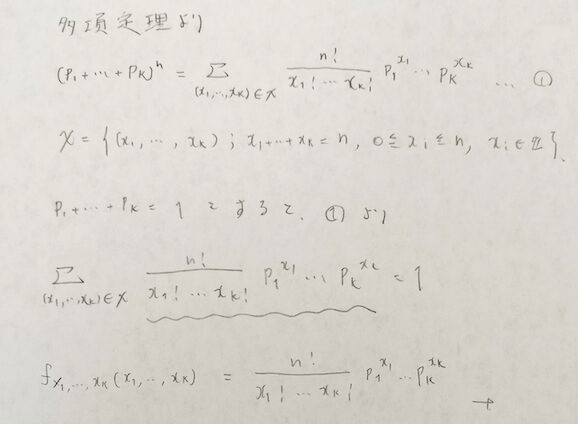
多項分布を二項にすると二項分布になります。多項分布の表記の仕方などをまとめます。
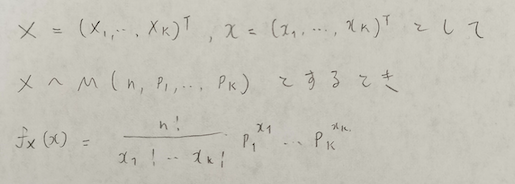
多項分布は多次元確率分布です。そのためベクトル表記を使用します。多次元確率分布は周辺分布を考えることがあります。多項分布は英語名『Multinomial distribution』の頭文字であるMを用いて表現します。
多項分布では順序統計量の簡易的な証明で用います。その際に表を持ち出すと大変便利です。多項定理の確率関数を例に表を紹介します。
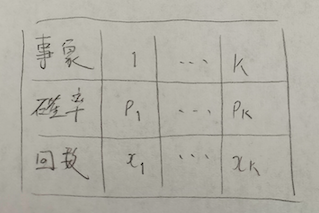
事象の部分は本来は集合表記ですが、今回は理解を大事にしてほしいと思ったのでこのような表記にしました。きちんとした事象の表記は記事の後の方(順序統計量のところ)で登場します。
多項分布の導出のところで全確率1は証明されていますね!
多項分布の積率母関数から期待値と分散を導出し共分散を求める
多項分布は多次元確率分布なので周辺分布の期待値や分散を考えます。そのため積率母関数から順に説明します。ここでも多項分布は二項分布の一般形であるという考えを用います。
まずは多項分布の積率母関数から導いてみましょう。
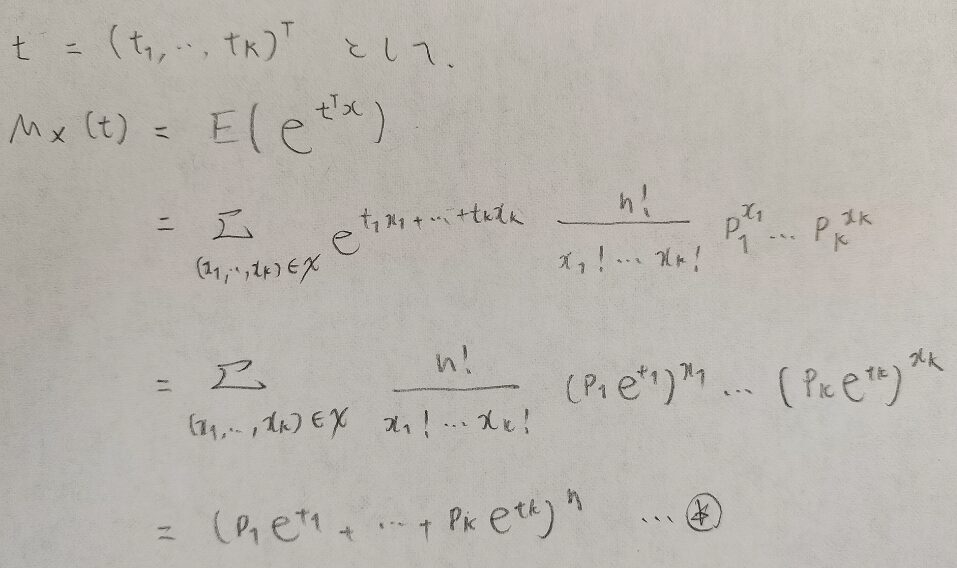
二項分布は多項分布の特殊な場合なので、ベクトルtの第i成分以外をすべて0にすることにより多項分布の周辺分布の期待値を求めることができます。その結果、多項分布の周辺分布が二項分布であることも確認できます。
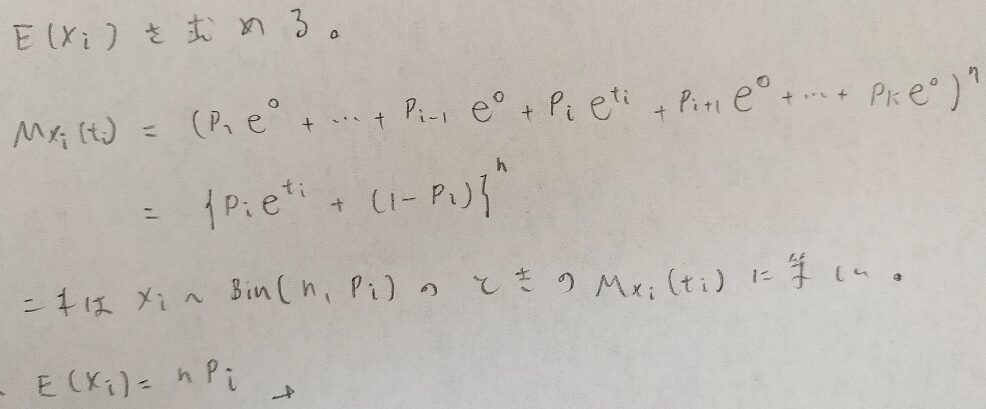
この☆の結果から多項定理の周辺分布を導けるのが面白いです!
分散については二項分布で既に勉強しているので結果はわかりますね。同様に二項分布で学んだ再生性も役に立ちます。
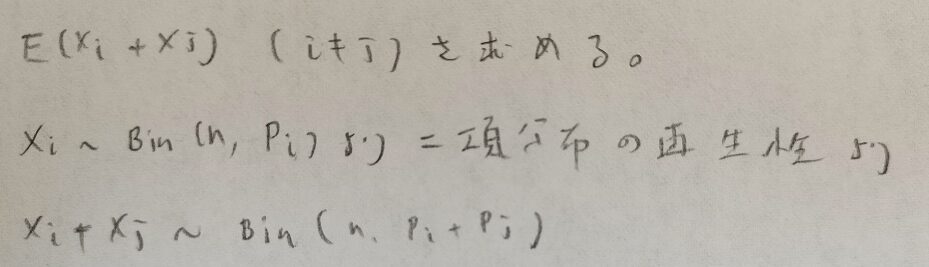
次に多項分布で注目すべき性質である共分散が負という性質を導きます。
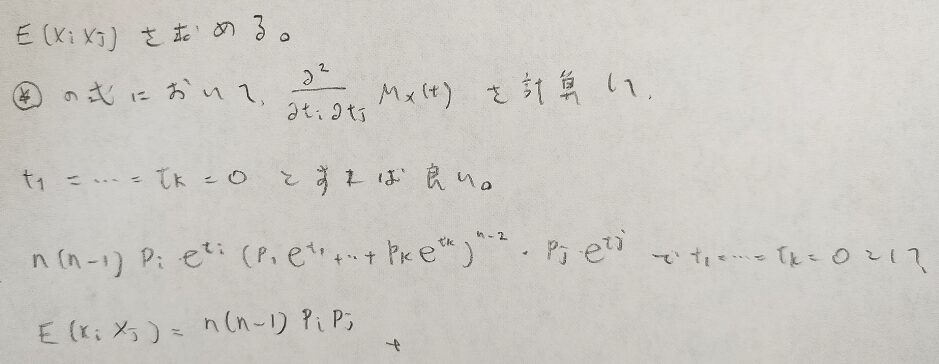
それでは共分散を求めます。
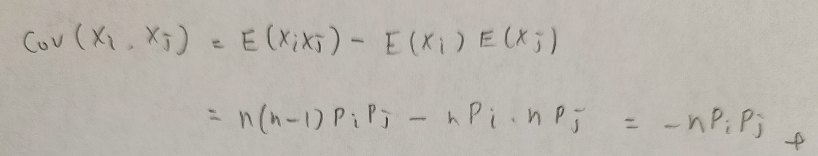
流れは分かりました。でもなぜ積率母関数を2回微分したら周辺分布の積の期待値が得られたのですか?
良い質問ですね。こちらは期待値の中身を微分してみれば理解できます。
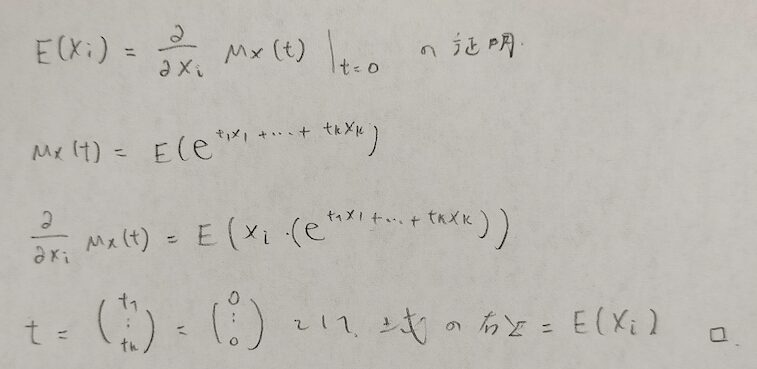
なるほど!もう1度微分すれば確かに周辺分布同士の積が登場しますね!
多項分布の周辺分布の共分散はアクチュアリー数学受験者は覚えておいた方が良いです。統計検定1級では結果だけを書くと減点される可能性が高いのでご注意ください。
ベータ分布の意味は順序統計量のあとで理解できる
ベータ分布の確率密度関数
いよいよ本記事の中核部分のベータ分布に入ります。
ガンマ分布がガンマ関数から作られたので、ベータ分布もベータ関数から作られそうですね!
それではベータ分布の確率密度関数を導きます。B(p,q)はベータ関数を表す記号です。
ベータ関数の記号B(p,q)はベータ分布の記号とは異なるのでご注意ください。
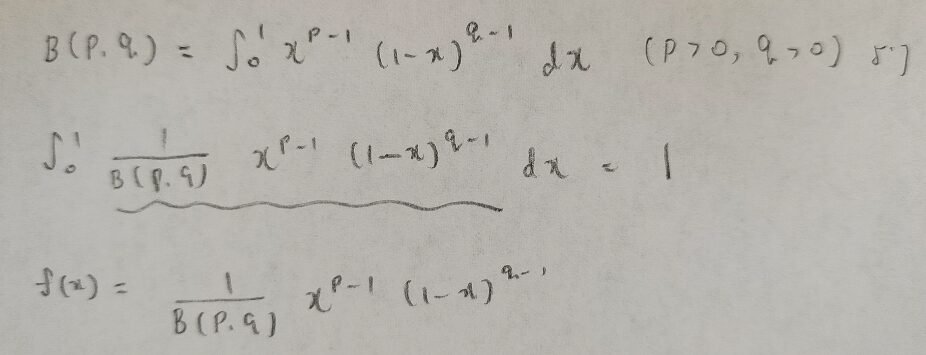
下の図のようにベータ分布は定義されます。ベータ分布はBeta(p,q)という記号で表します。ベータ関数B(p,q)の独立変数xの定義域がそのままベータ分布の実現値xの範囲になります。
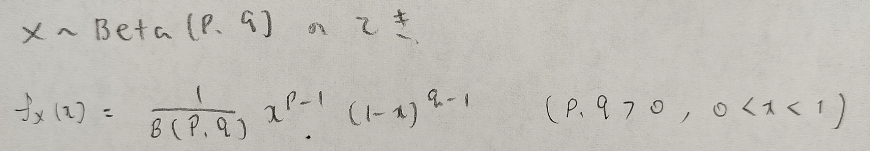
ベータ関数はさまざまな性質があります。それらを駆使してベータ分布のいろいろな性質を導いていきます。
ベータ関数の性質とその証明
ベータ関数の持つ性質を調べていきます。まずはベータ関数単体の内容でガンマ関数との絡み、そして(『弱点克服 大学生の確率・統計』を参考にして)一見気づきにくい性質まで扱います。
ベータ関数のパラメータに関する交換法則
まずは最も簡単な性質から証明します。ベータ関数関連では置換積分が主な計算手法になります。
ベータ関数の性質の証明で用いる置換積分は初見では気づきにくい置き換えが多いです。ペンを片手に一緒に計算してみましょう。
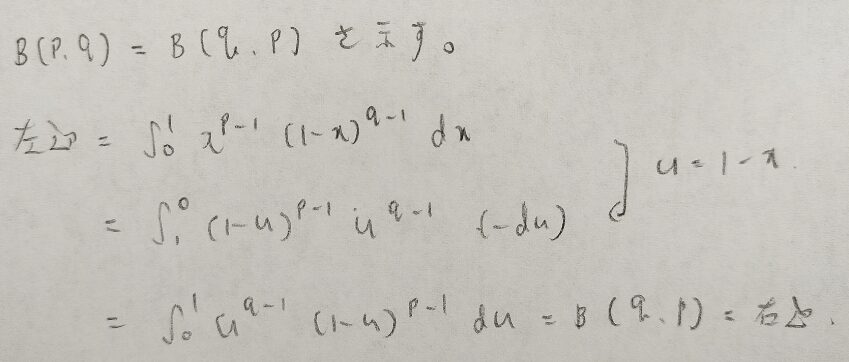
ベータ関数と三角関数(正弦カーブ)との関連
ベータ関数はサインカーブと相性が良いです。受験数学ではウォリスの公式として登場した積分漸化式の一般形となっています。
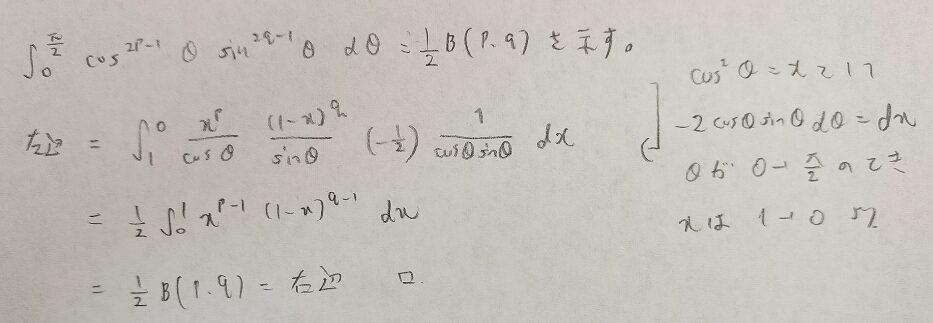
受験数学とつながっているのは感動です!
ベータ関数とガンマ関数との関係
三角関数の積分をベータ関数に置き換えられても、ベータ関数は積分で定義されているから計算が面倒じゃないんですか?
実はガンマ関数とベータ関数には関係性があります。ガンマ関数は階乗計算に帰着できるので、ベータ関数もパラメータが整数の場合は階乗計算に帰着されるのです。いまから紹介する公式はベータ関数の重要公式です。
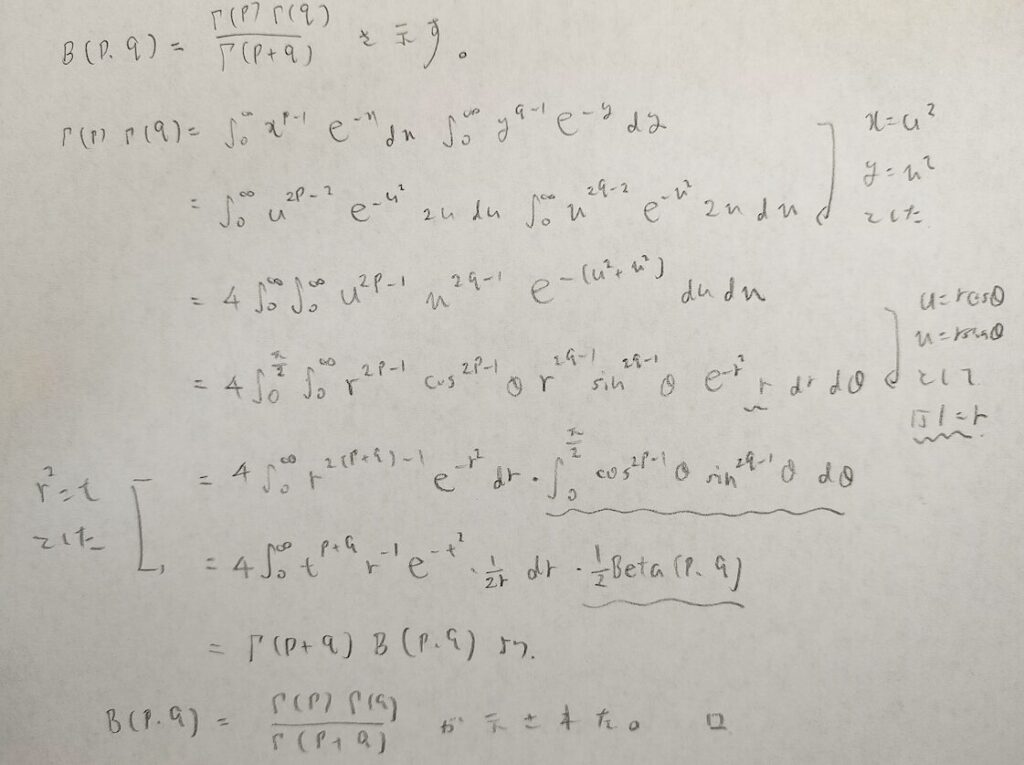
置換積分とてもしていますね。
この性質の証明問題は数学検定1級の2次検定のレベルです。要するに大学数学の内容の中ではかなりの頻出問題です。しっかりと証明できるようにしておきましょう。数学検定1級の参考書は『合格ナビ!数学検定1級1次 解析・確率統計』『合格ナビ!数学検定1級1次 線形代数』が現時点でベストです。
ベータ関数と分数関数との関係(アクチュアリー数学)
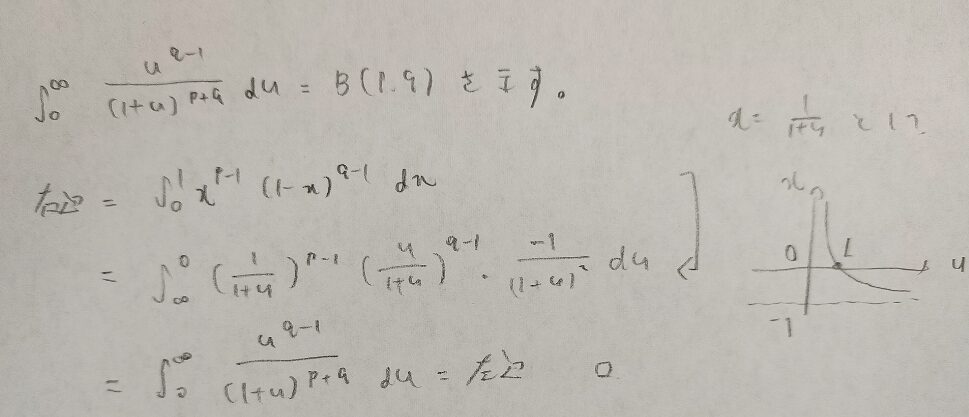
アクチュアリー数学の参考書『アクチュアリー試験 合格へのストラテジー 数学』などで頻繁に登場する公式です。
これを初見で「ベータ関数だ!」と気付けたらかなり凄い人です!
置換の方法は分数関数だから分数関数で置換しようという単純な発想で覚えました。
ベータ関数の性質はここまで学習すれば十分です。いよいよベータ関数の性質を調べていきます。
ベータ分布の期待値と分散と高次モーメント
ベータ分布の期待値を求めましょう。
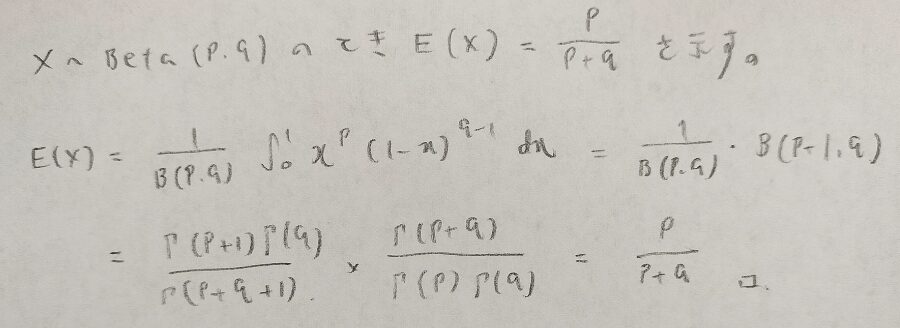
ベータ関数の性質がさっそく使われていますね。ガンマ関数に落とし込むことが計算のコツなのですね!
ベータ分布の分散も計算してみましょう!
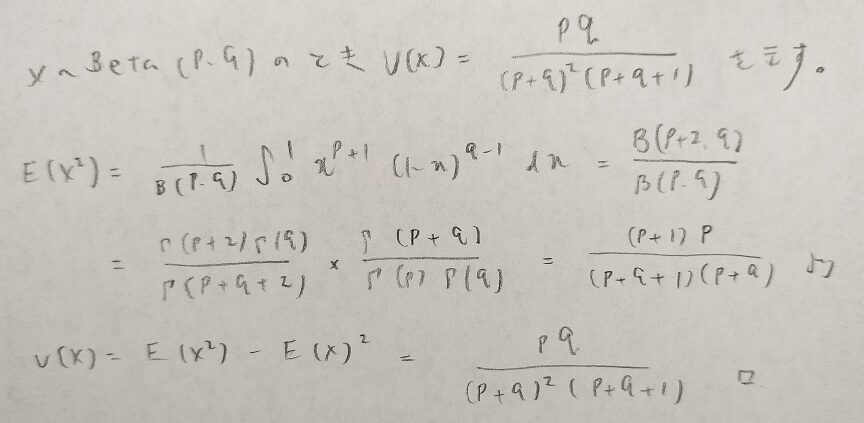
期待値のときとほぼ同じ流れですね。1番気をつけないといけないのは最後の通分の部分かも知れません笑
期待値の2乗もできたので一般化してみましょう。ベータ分布の高次モーメントも算出しておきます。
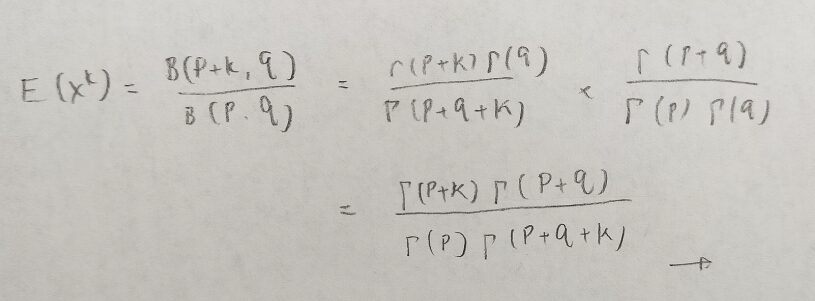
みんな一緒ですね!笑
ベータ分布は計算方法にさえ慣れてしまえば計算自体はこわくないですよ!難しいのはベータ関数の持つ意味の方です。
ベータ分布の持つ意味は順序統計量が絡んでいます。順序統計量はこの章のあとで解説します。
ベータ分布の性質(変数変換の利用)
ベータ関数の性質を終えてベータ分布の期待値と分散などを通してベータ分布にも慣れてきたと思いますので、いよいよベータ分布の持つ性質へと進みます。ここではガンマ分布との関連性を目標に進みます。
ここでは変数変換がかなり登場します。ゆっくりと進めていきましょう。ヤコビアンを用いない1次元以上の変換方法として『リスクを知るための確率・統計入門』を参考にテクニックを紹介しています。
ベータ分布のパラメータの入れ替えに関する確率変数の変換
まずはベータ分布の持つ最も基本的な性質からスタートします。
ベータ関数にパラメータの入れ替え法則があったように、ベータ分布のパラメータを入れ替えるにはどのような変数変換をしたら良いのでしょうか。
X~Beta(p,q)のとき1-XとすればOKです。証明はやってみると(分布関数を避けるならば)簡単です!
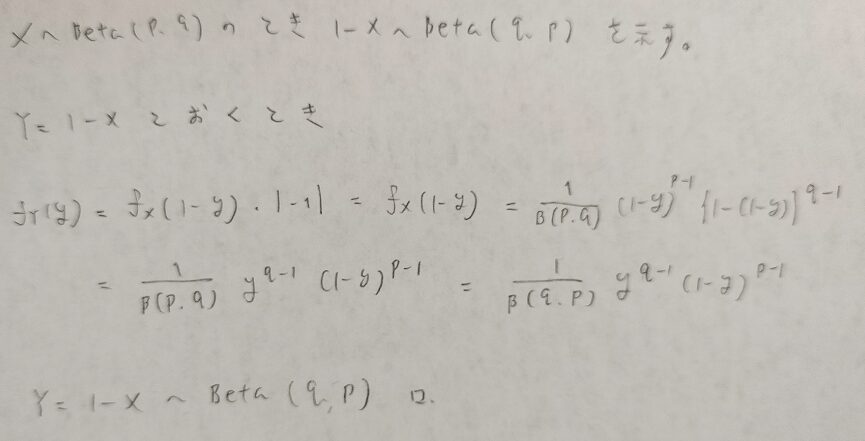
1-Xとするのはベータ関数の積分の形から納得ですね!
ベータ分布とガンマ分布との間の確率変数の変換式
この定理に登場する変数変換をヤコビアンを用いずに解いてみます。ヤコビアンを用いない1次元以上の変換方法として『リスクを知るための確率・統計入門』を参考にテクニックを紹介します。
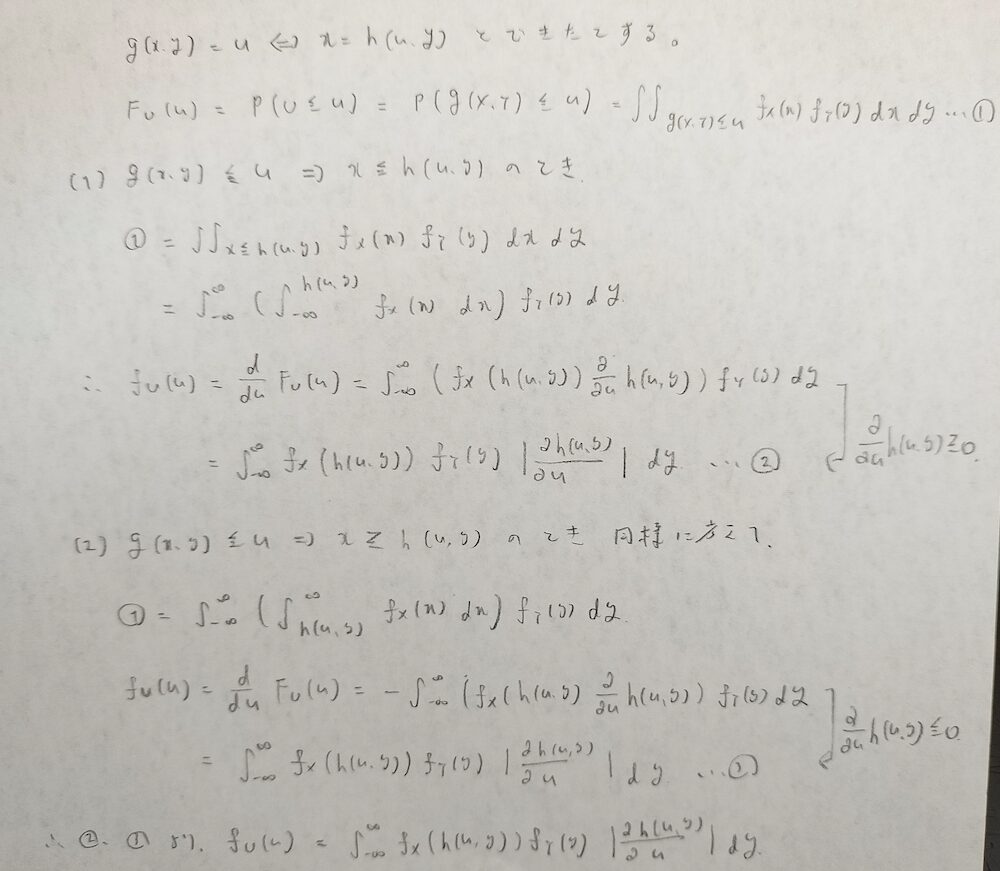
岩沢先生のテクニックを用いて2つの独立なガンマ分布をベータ分布に変換する方法を考えましょう。
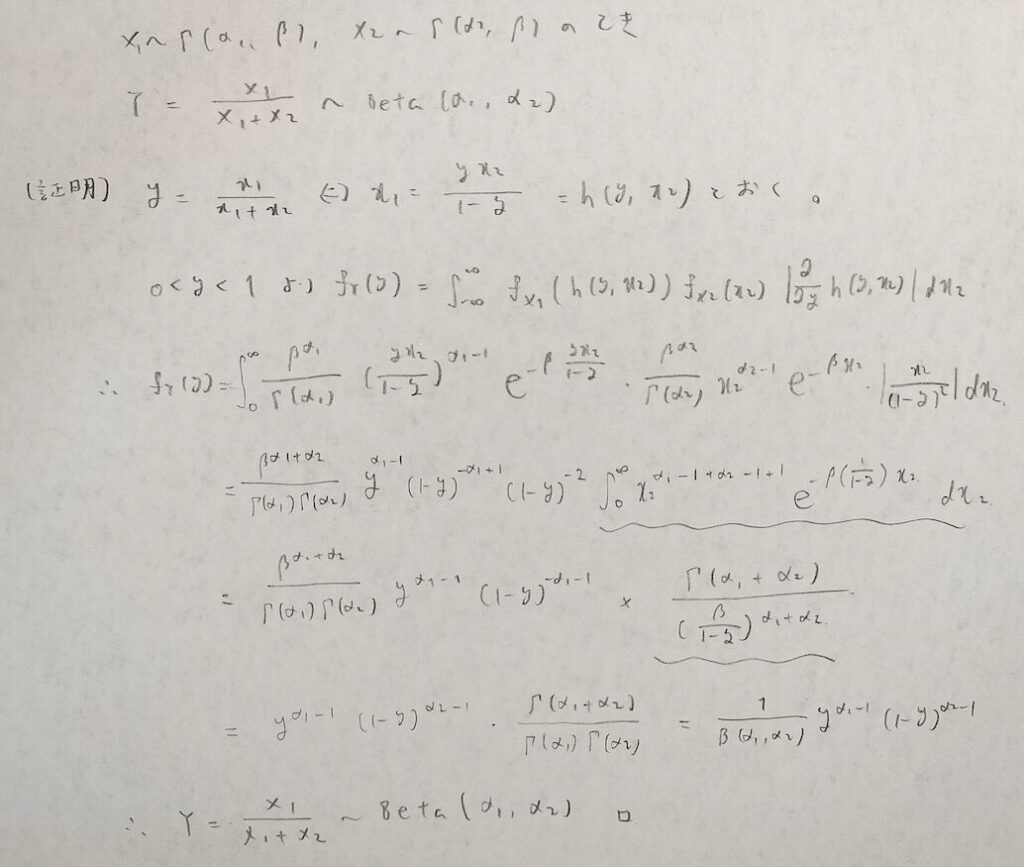
これでベータ分布の計算面は終了です。
残ったのはベータ分布がどのような意味を持つ分布なのか?ですね。
ガンマ分布(アーラン分布)は指数分布(イベント発生間隔が従う分布)の和の分布なので待ち時間に関係する分布でした。ではベータ分布は一体どのような意味を持っているのでしょうか。そのためには順序統計量という概念の理解が必要になります。
順序統計量:分布関数と確率密度関数について
ベータ分布の意味を理解するために順序統計量を定義して性質を調べます。
Pは確率分布で、そこからn個の標本(サンプル)をとります。Pは無限母集団を仮定しているので、n個の標本は独立です。
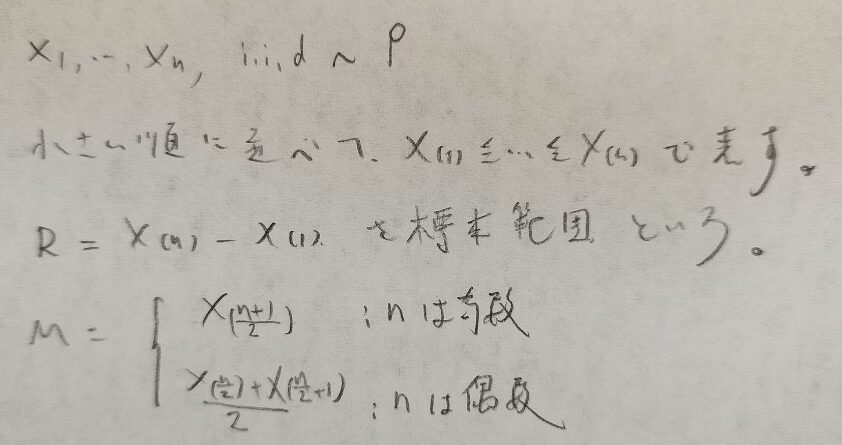
一番小さいものを最小統計量、一番大きなものを最大統計量といいます。(離散確率変数と比べてメインの)連続確率変数を考えるときに、それぞれの分布関数を求めてから確率密度関数を考えましょう。
順序統計量の分布関数と確率密度関数
突然に一般化すると難易度がとても上がり理解が難しいと思われます。そのため最大統計量→最小統計量→一般化と簡単な順に考えていきます。
最大統計量からお願いします!
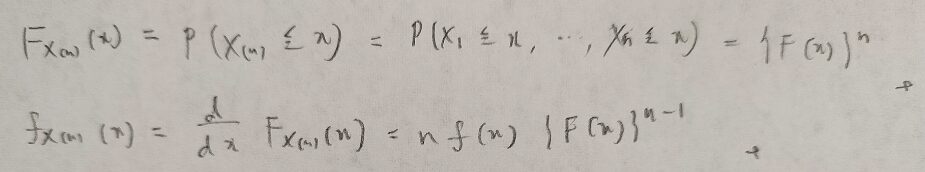
こちらになります。離散型の場合はシグマを用いますが後ほど紹介します。
最小統計量もお願いします!
こちらは生存関数を用いて考えると混乱を防げます。
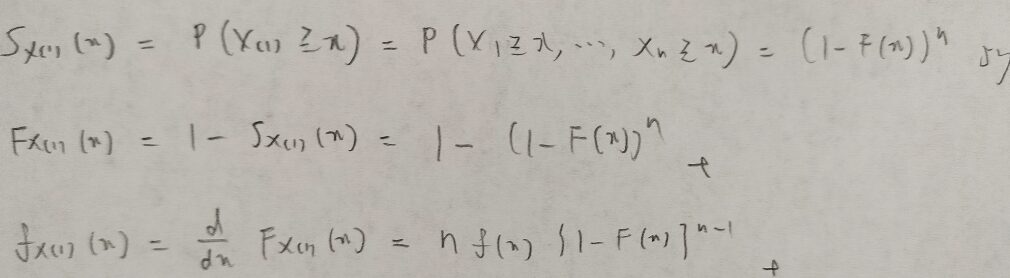
それでは一般化します。一気に難易度が上がりますので落ち着いて落ちついて着いてきて下さい。ポイントは①式の理解です。
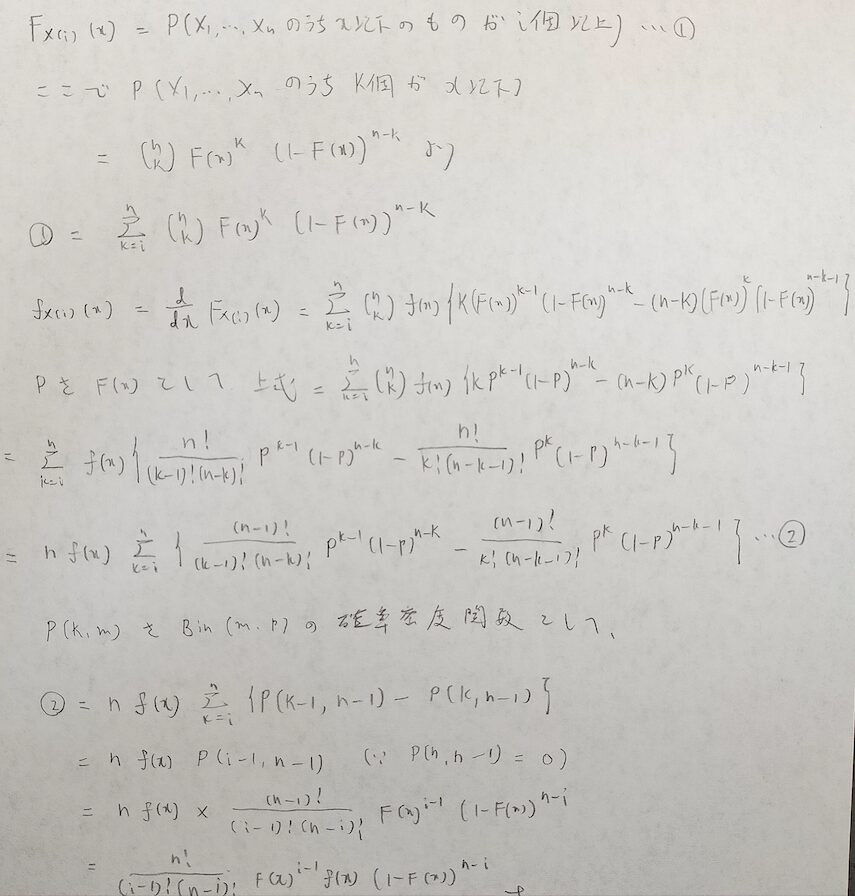
とても難しいです。
二項分布が出てくるところが難易度高いと思いますよね。これは何回か見直さないと頭に入らないと思います。反復が大事です。
ベータ分布を扱うときはベータ分布は連続確率分布なのでこの公式でOKですが、離散分布の場合も分布関数と確率関数を求めておきます。ポイントは受験数学で勉強した玉ねぎ型確率です。(玉ねぎ型確率は『合格! 数学I・A 新課程』に分かりやすく載っています。受験数学では頻出な問題でP(X=k)=P(X≦k)-P(X≦k-1)とするタイプです。)連続確率分布でこの作業に相当する作業が微分になります。
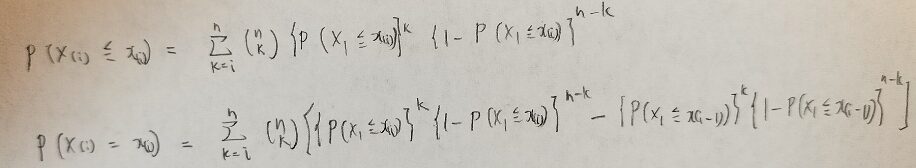
分布関数を出すところは二項分布を使うので連続型のときとほぼ一緒の考え方です。分布関数から確率関数を出すところは玉ねぎ型確率の考えです。
多項分布を用いて順序統計量の確率密度関数を分布関数を経由せずに求める方法
この記事の序盤に出てきた多項分布はいつ役立つのですか?
良いタイミングです。今まさにそのときが来ました!
順序統計量の分布関数の導出に二項分布が出て来ました。しかし(連続型の場合は)分布関数を微分する必要がありました。多項分布を用いる方法では分布関数を経由せずに一気に確率密度関数を求めることができます。
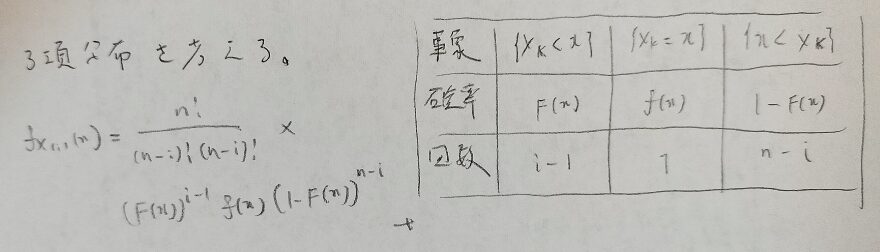
これはエレガントですね!多項分布は表を用いて考えると便利だとよく分かりました!
次に順序統計量の同時分布を求めます。先ほどより難しいですが同じような考え方で綺麗に導くことができます。

この問題の一般化(次の問題)の証明が過去に2回ほどアクチュアリー数学に出題されました。
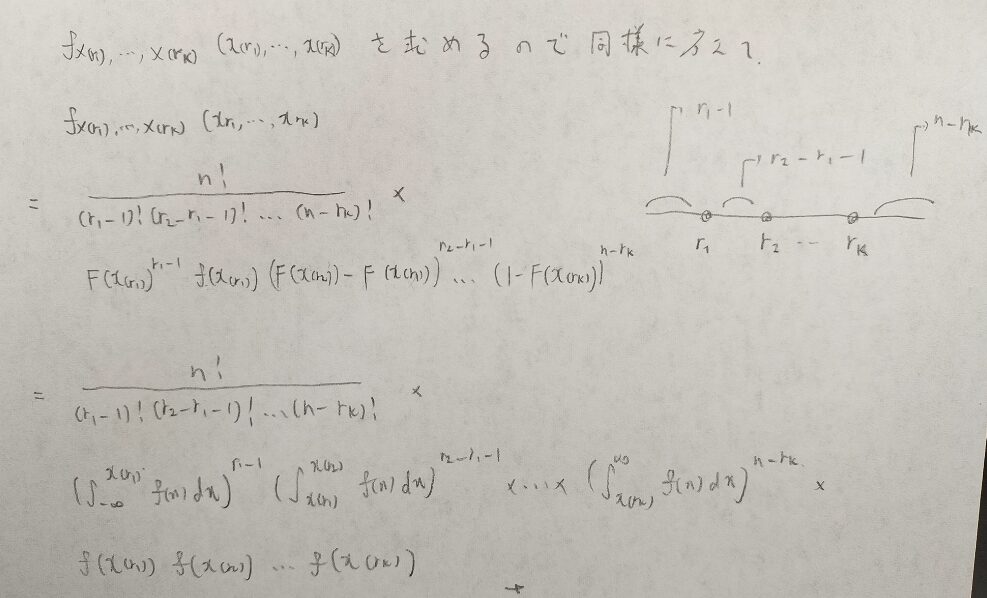
こちらはアクチュアリー数学では頻出なので受験者は覚えておいた方が良いです。
最後はn個すべて用いるタイプの同時分布を考えます。この問題の解き方は『現代数理統計学の基礎』系列の久保川先生の著作にのみ掲載されています。
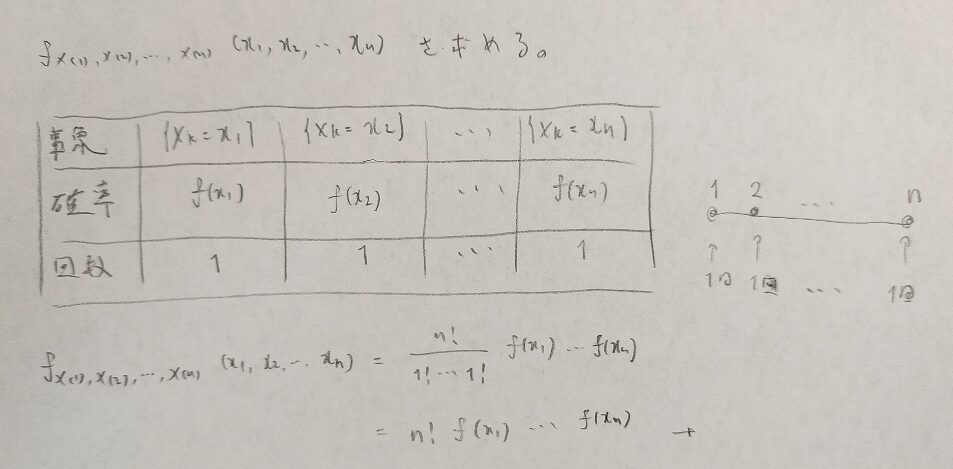
順序統計量の範囲の分布
ベータ分布が順序統計量とどのように関係しているのか?に答えるためには、あともう少しだけ順序統計量を深掘りする必要があります。
頑張りますので、よろしくお願いします。
今回は順序統計量の同時分布の公式は理解した上で、差の分布も同時に考えるので、順序統計量のラスボス的な存在感です。
順序統計量の範囲の分布は難しいので、こちらも具体例→一般化へと進んでいきます。まずはイメージしやすい最大統計量ー最小統計量(標本範囲)が従う分布を求めます。
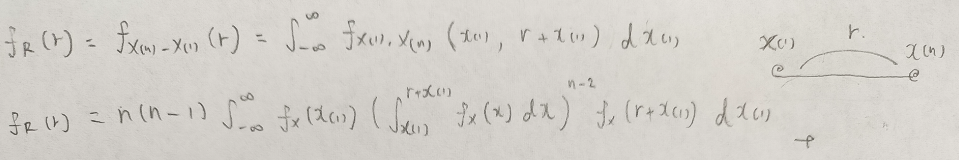
では、一般化します。複雑になりますが、上の問題とほぼ同じように考えればきちんと答えにたどり着けます。
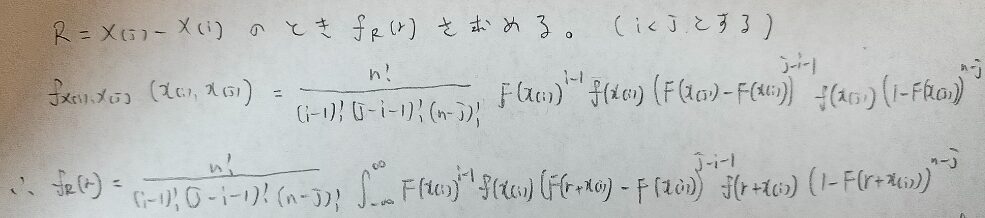
ベータ分布の意味
ベータ分布はXが標準一様分布に従うときに小さい方から数えてp番目で大きい方から数えてq番目のものが従う分布のことです。
なぜ標準一様分布が出てきたのでしょうか?下の解説をご覧ください。
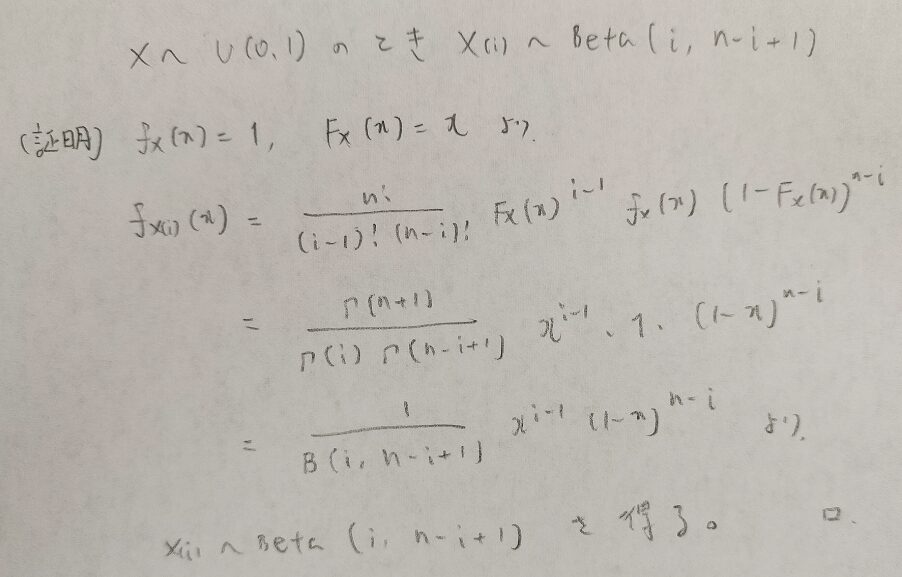
数式で進めると納得できます。一様分布と順序統計量のコラボレーションで生み出された分布がベータ分布だったのですね。どうりで結論までが長かったわけです笑
そして標準一様分布ならではの超有名な公式があります。アクチュアリー数学の受験者は超頻出な公式なので覚えていくださいね!
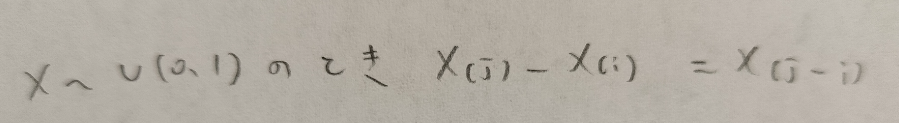
証明は円周の長さが1の円上にPを固定して残りn個の点を打って考えれば、自明な結論となります。
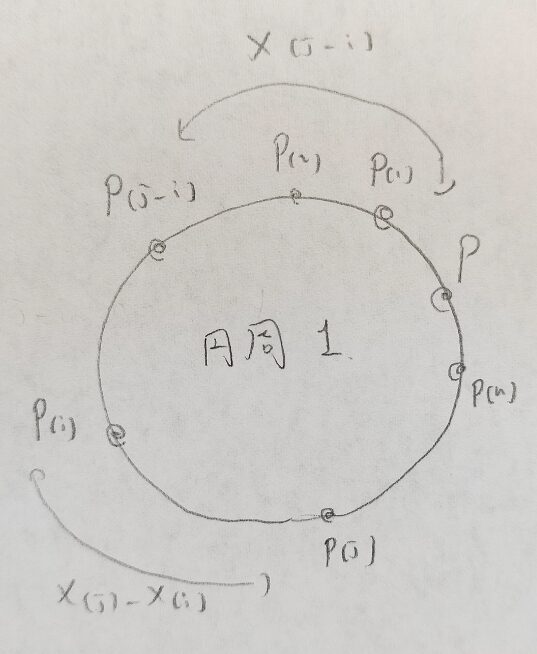
順序統計量とベータ分布と一様分布が合体した例(アクチュアリー数学過去問より)
区間(0,1)の中で、3つの実数を無作為に選ぶ。このとき、最も小さい数の期待値を求めよ。
アクチュアリー数学(H15)
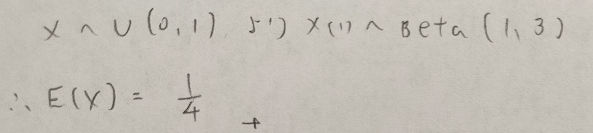
1/3じゃないのが不思議な問題です。
感覚的にはほぼ当たらない名問です。
2つの確率変数が独立にU(0,L)に従うとき、2つの確率変数の差の絶対値のn乗の期待値を求めよ。
アクチュアリー数学(H13)
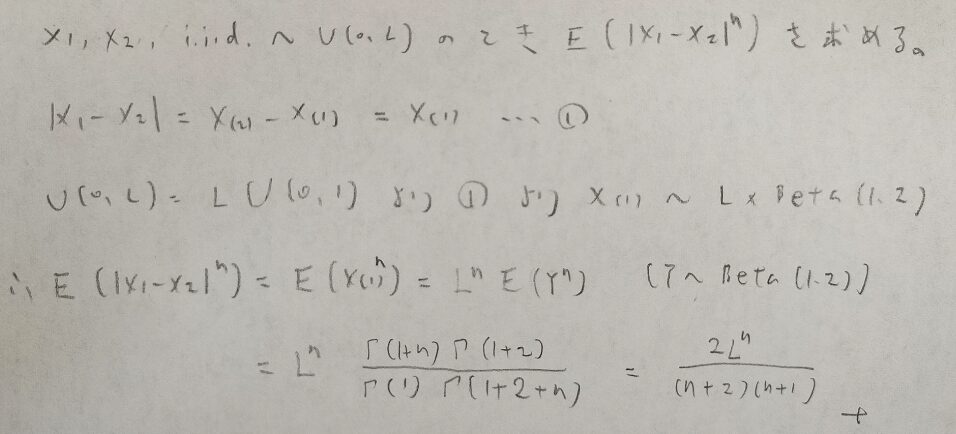
アクチュアリー数学の難しさはこのような問題は1分程度で解かないといけないところです。
ベータ分布の期待値は知っていないとアウトなわけですね。
ようやくベータ分布も終わりに近づきました。ここで二項分布と負の二項分布と標準一様分布とベータ分布の間の関係式をまとめて終わります。
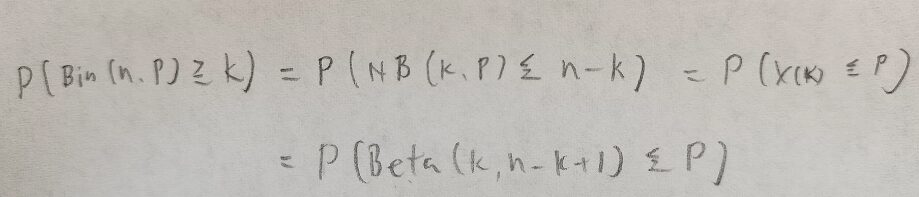
標準一様分布のところのイメージ図はこちらです。
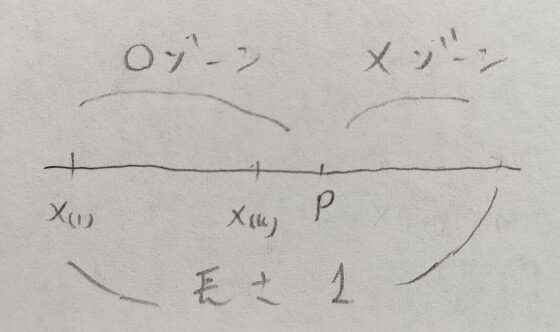
ディリクレ分布は多次元ベータ分布のこと
ベータ分布を多次元にしたものをディリクレ分布といいます。
まだあるのですね笑
ガンマ関数との絡みがより深められる良い機会ですので、最後まで一緒に頑張りましょう!
まずはディリクレ分布の確率密度関数をベータ関数(多次元バージョン)から導いてみます。
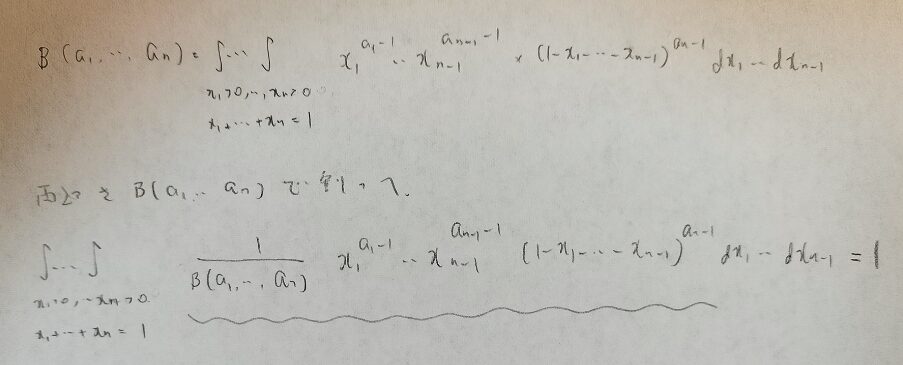
ここの波線部分がディリクレ分布の確率密度関数になるのですね!
ディリクレ分布の全確率1は上の数式から導かれていますね。
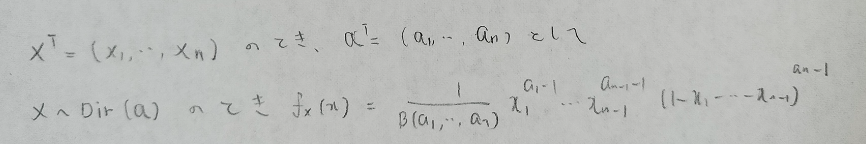
ディリクレ分布の期待値を求めましょう。
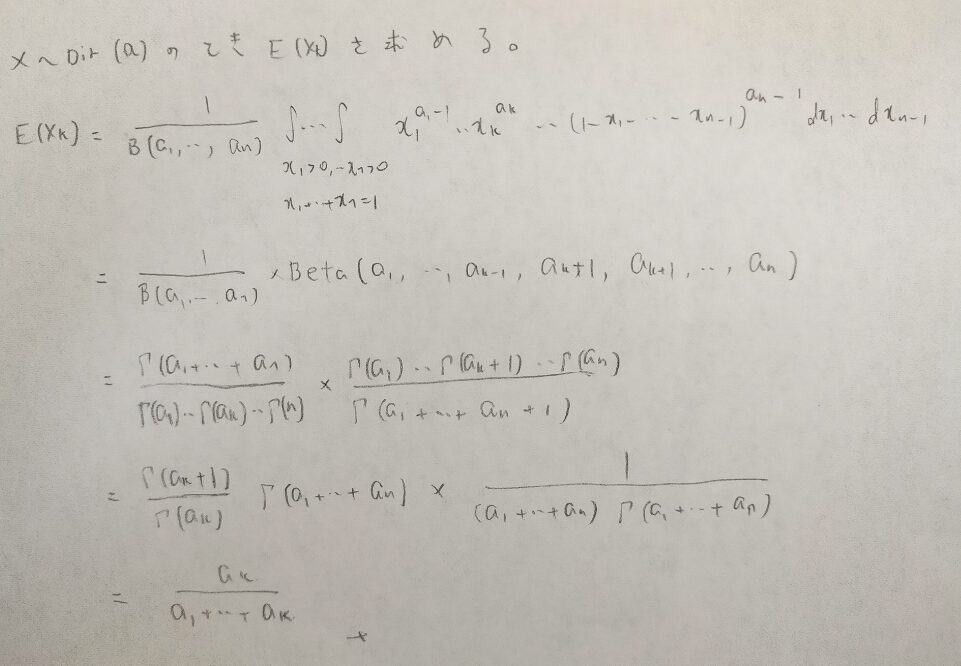
ベータ分布のときと似てますね。期待値の結果を見ても、ディリクレ分布はベータ分布の一般化だとよく分かります。
しかしこの解答はベータ分布とガンマ分布の関係(下から3行目)をしれっと用いているので、本当に多次元でも成立するのか?を証明しておく必要があります。
この問題はディリクレ積分をきちんと証明できればOKです。とても複雑なのでこの記事の最後に証明します。
次にディリクレ分布の分散を求めますので、まずは2次モーメントを求めます。
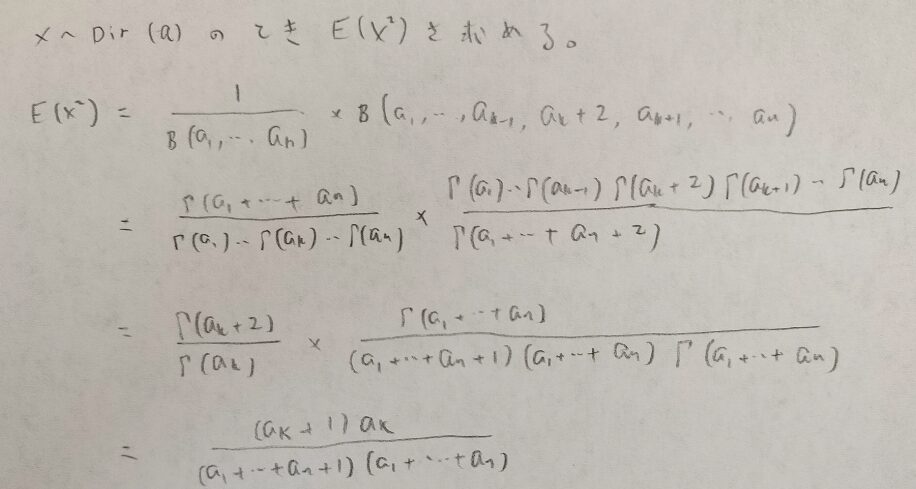
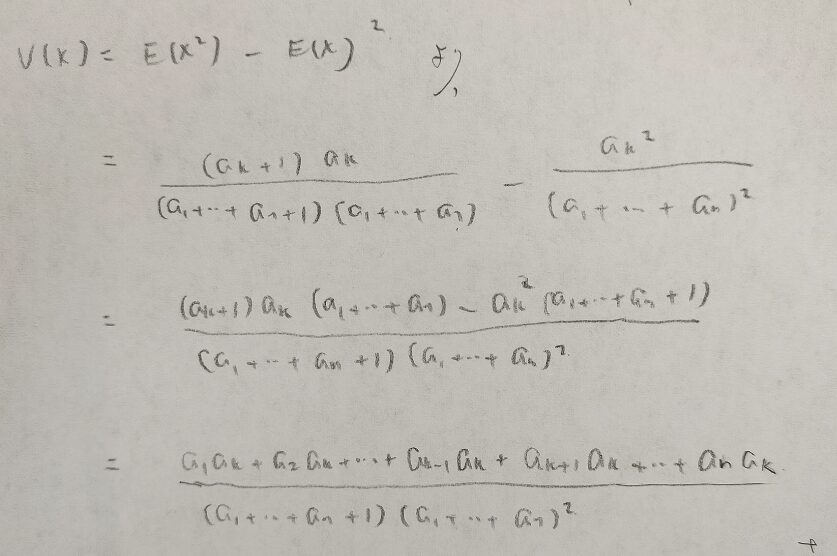
この結果はこれ以上きれいにならないので、これを最終結果とするのが一般的です。
『アクチュアリー試験 合格へのストラテジー 数学』ではディリクレ分布(多次元ベータ分布)の性質が載っていますので掲載しておきます。
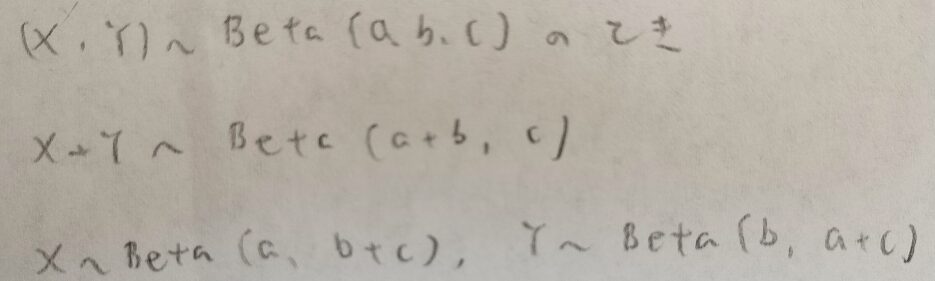
ディリクレ積分
本記事の最後にベータ関数とガンマ関数との間の関係式を多次元に拡張した定理を証明します。
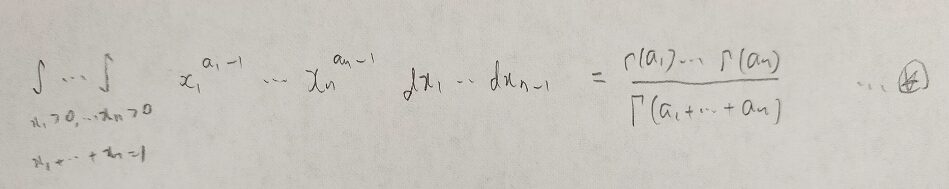
いよいよラストスパートです。一緒に頑張りましょう!
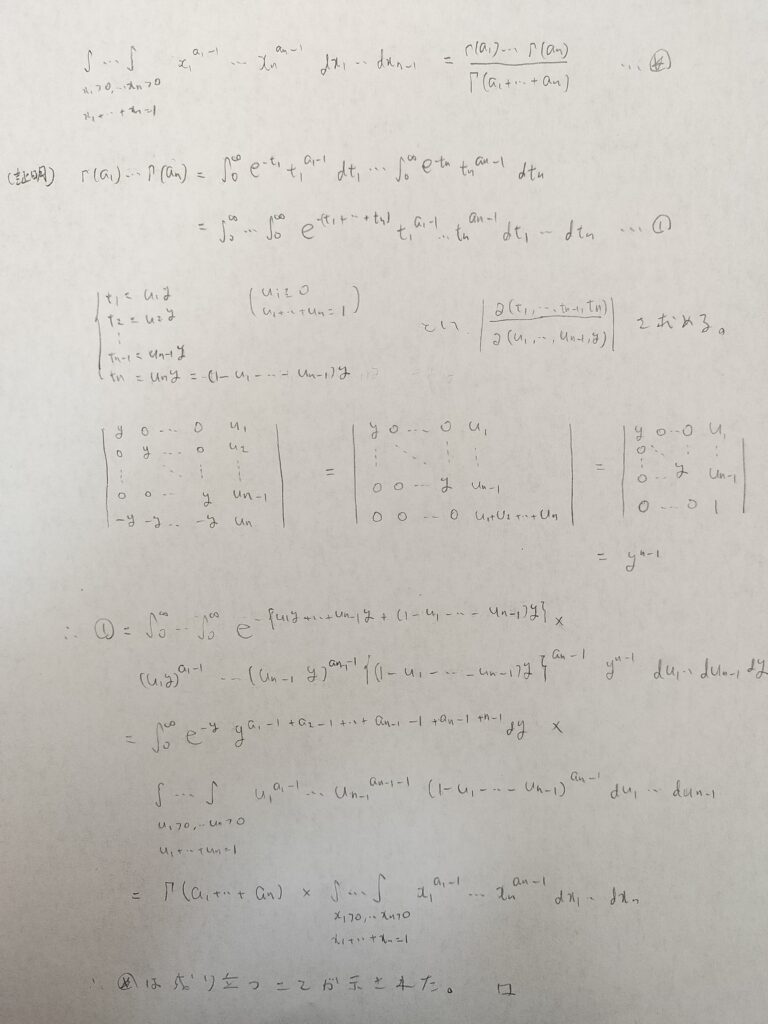
お疲れさまでした。最後に多項分布とベータ分布とディリクレ分布の内容で参考にした書籍を紹介します。
玉ねぎ型確率の紹介で参考にしました。本書は到達点が高いのでおすすめです。問題量は少ないですが、超進学校でもない限り、本書をこなせれば定期テストは100点取れます。到達点は1対1対応の演習の少し下程度です。欠点は問題量が少ない点です。本書は理解度を重視する参考書です。また中学生が高校数学を予習する用途でも良いと思います。
ベータ関数とガンマ関数の絡みに関しての問題が豊富です。弱点克服と書いてありますが、これをこなせればかなりの実力者です。
ベータ分布の意味のところで参考にしました。本記事のテーマとなった部分です。ヤコビアンを用いないで変数変換を行うテクニックが書かれているのは本書だけです。
名著です。本書にしか載っていない定理がありまして、本記事ではその定理を使用しました。統計検定1級対策で最も有名な参考書です。
ディリクレ分布(多次元ベータ分布)の図形問題への活用例が豊富です。
数学検定1級の箇所で紹介しました。解析学と統計学の問題が過去問をベースで掲載されています。現時点の数学検定1級の対策本として最もおすすめできる名著です。
数学検定1級の箇所で紹介しました。線型代数の問題が過去問をベースで掲載されています。現時点の数学検定1級の対策本として最もおすすめできる名著です。到達点は数学検定1級に合格できる程度の線型代数のレベル感です。東大院試などの院試には届かないので、院試を考えている方は院試対策用の線型代数『線形代数学[新装版]』などでしっかりと基礎固めをしましょう!