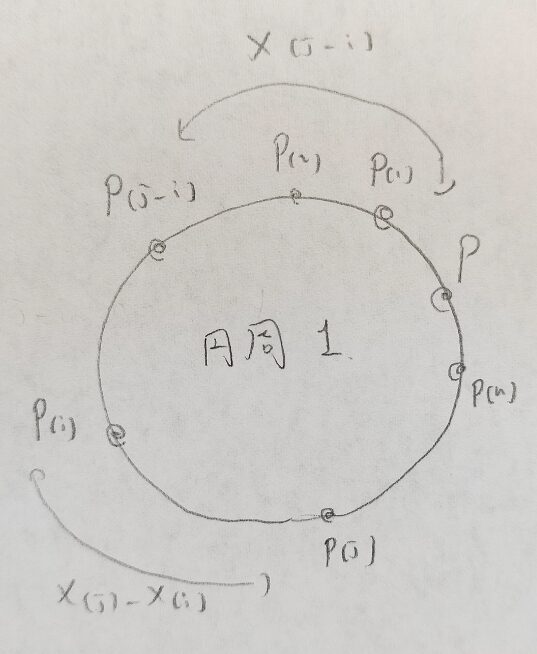
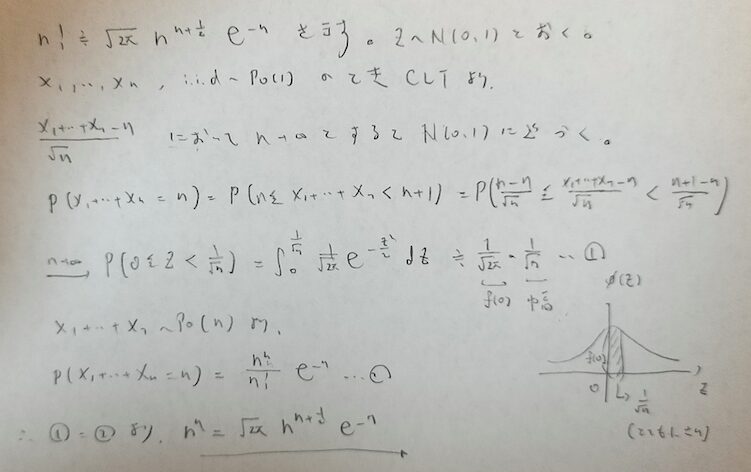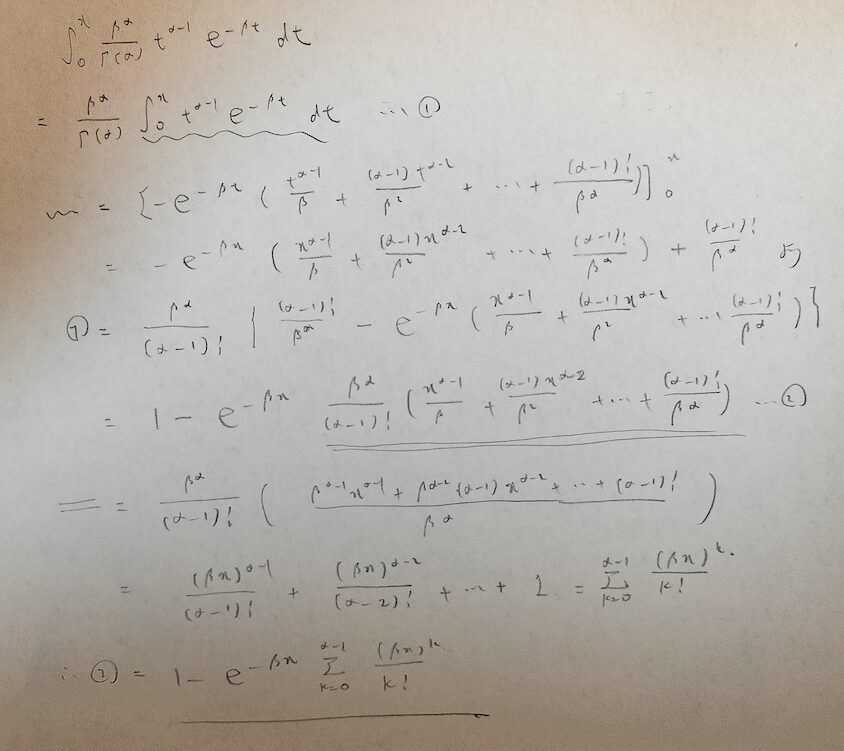正規分布で出てきた中心極限定理(CLT)を覚えていますか?
このようなものでしたよね!
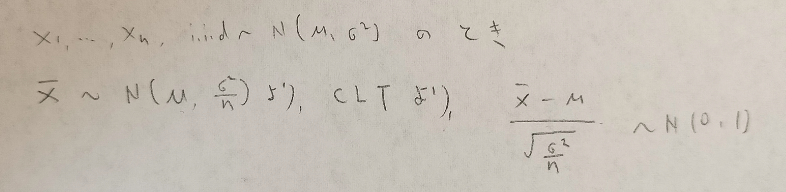
期待値と分散を持つ同一の確率分布からの標本の和は正規分布に近づいていくという内容が中心極限定理でした。
しかしここで分散(標準偏差=σ)がわからない場合は、困ったことになります。n個の標本のみでどうやってN(0,1)などの確率分布を探っていくのでしょうか?☆
ゴセット(Gosset)はこの問いに答えを導き出しました。(『統計学大百科事典 仕事で使う公式・定理・ルール113』より)ゴセットの論文を冠してスチューデントのt分布というものがその確率分布になります。☆のように考えて統計量を作ることをスチューデント化といいます。
中心極限定理から出発して、t分布が登場する流れを理解し、実際にt分布の確率密度関数を求める流れを行うことによって、スチューデント化を一緒に体感していきましょう。
t分布の自由度をわかりやすく説明
t分布が出てくる背景とt分布の定義
まずこの一連の流れをご覧ください。分散を不偏分散(標本分散の定数倍)でスチューデント化する様子です。
要するにσの2乗をUの2乗で置き換えたらどうなるか?という話ですね!
5行目の式で中心極限定理を用いています。ここが式変形で難しいところです。
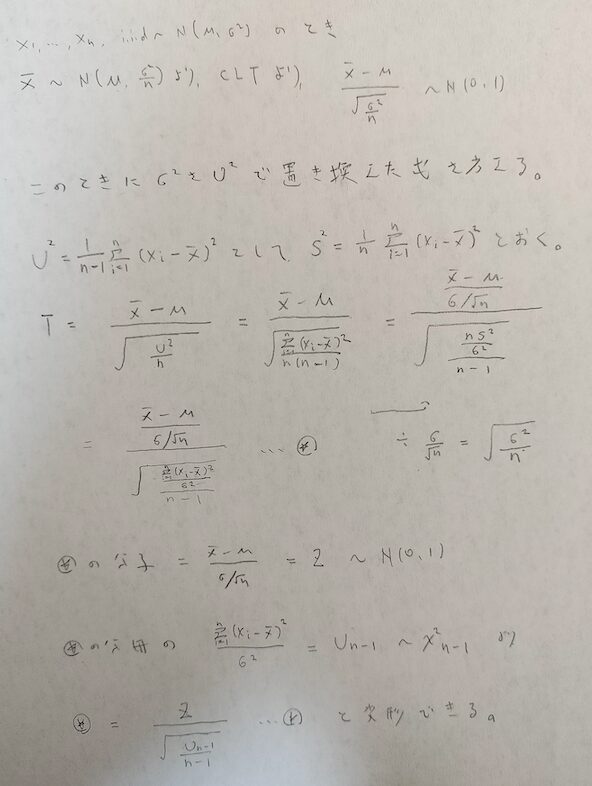
最後の❇︎の式がどのようになるかが分かれば❇︎がどのような確率密度関数になるかがわかりますね!
さっそくt分布について定義しておきましょう!
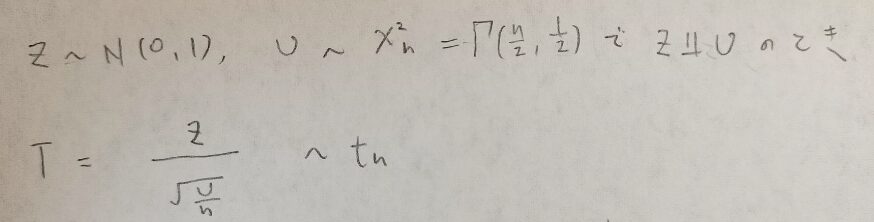
自由度nのt分布は分母に自由度nのカイ2乗分布を用います。単なる2乗和のことではないのでご注意ください(混乱の元になります)
t分布の確率密度関数の導出
自由度nのt分布の確率密度関数を求めていきます。こちらは2変数の確率変数の変換を行なったあとにtの周辺分布を求めていく方法をとります。
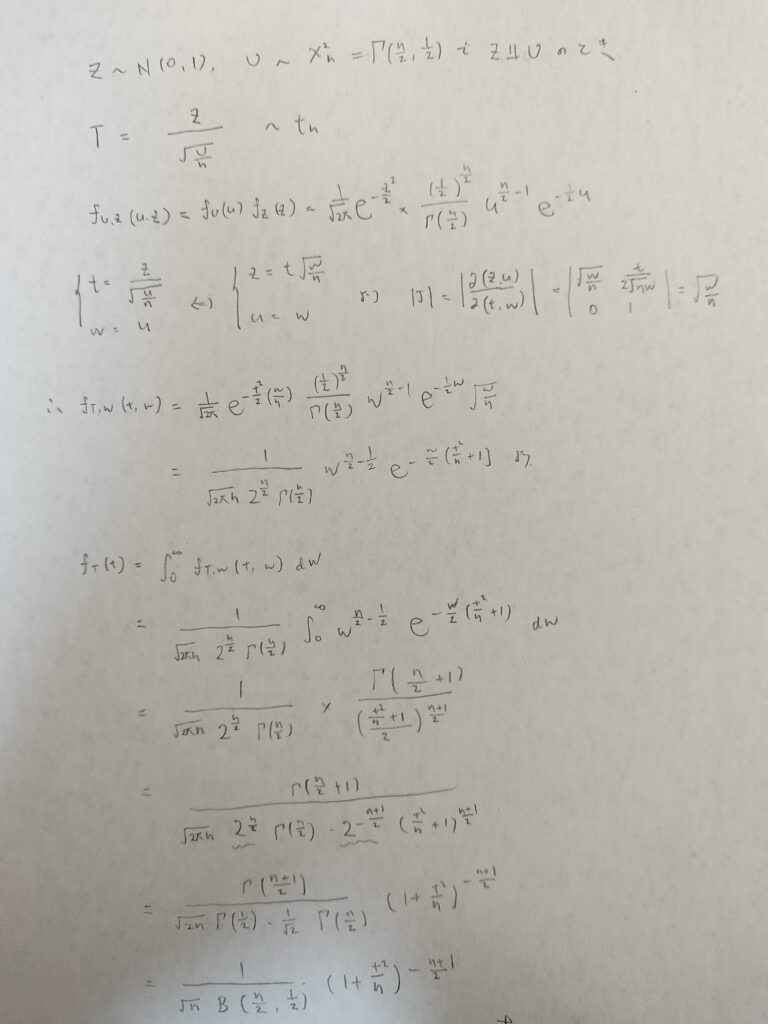
ベータ関数が出てきましたね!前回の記事で勉強しておいて良かったです。こうすれば覚えやすいですね。
アクチュアリー数学では2020年からt分布などの確率密度関数を覚えておかないと時間切れになる傾向があります。ベータ関数の中身は、ガンマ関数のときだと自由度nのカイ2乗分布に等しいので関連性があって、覚えやすい形だと思います。
t分布はとにかく自由度が混乱しやすいです。そのためここでt分布の自由度に関することをまとめておきます。
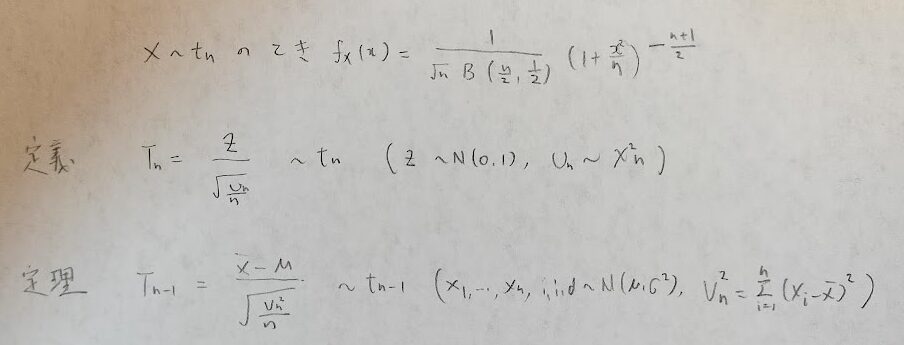
t表で重要なt分布の全確率1の証明
t分布はt表などの理論面でも実践面でもとても大切な分布です。そのため全確率1を証明しておきましょう。
ベータ関数が再び登場しますので、ベータ分布についての記事を未読の方は下のリンクよりご覧ください。
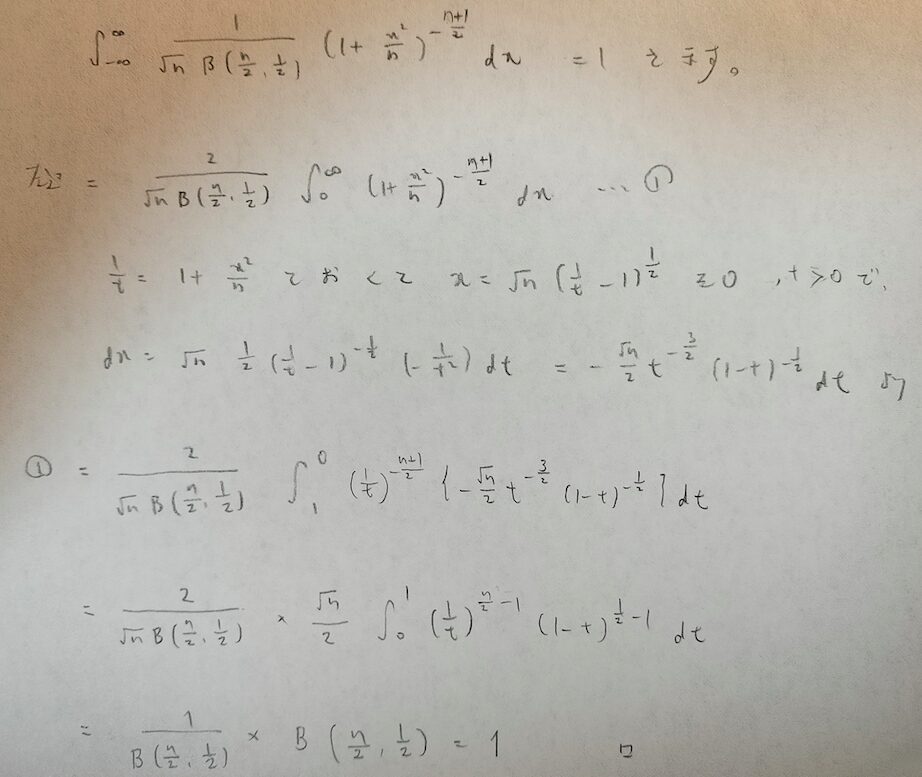
最初の置換積分で1/tとおくのは最後のベータ関数を見据えてですね!
この証明は『明解演習 数理統計』を参考にしました。本書には類書にはない重要な問題が多く掲載されています。
t分布の期待値と分散
t分布の期待値と分散を求めていきます。
ガンマ関数の定義域が正の理由から途中で場合分けが出てきますので、n=1のときはどうなるんだろう?という気持ちで眺めてください。
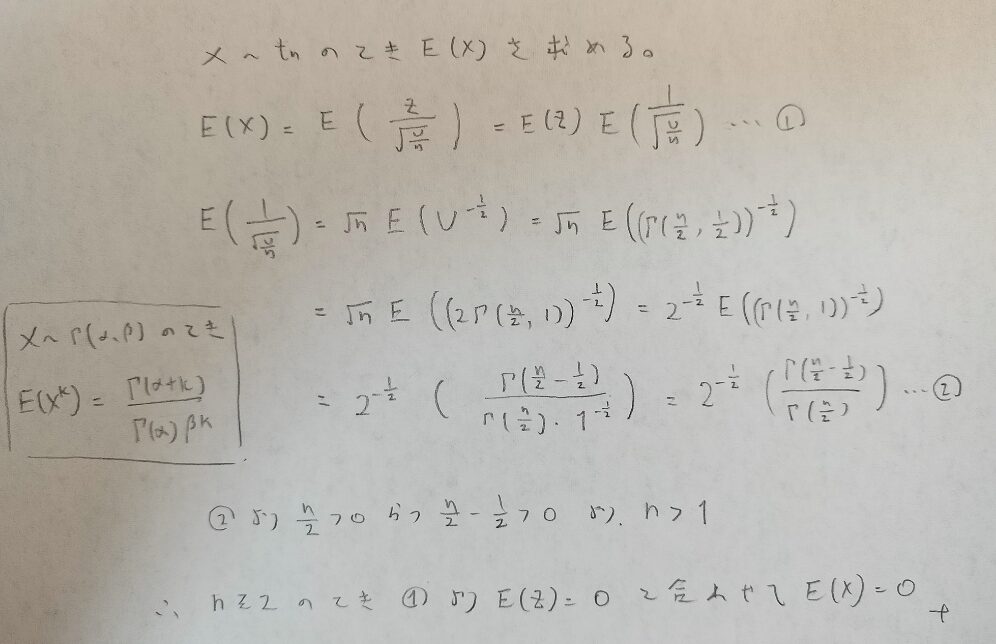
t分布はnが1以外のときは標準正規分布と同じように期待値が0でした。
自由度1のt分布は何か特別感がありますね。
t分布の分散も求めてみます。
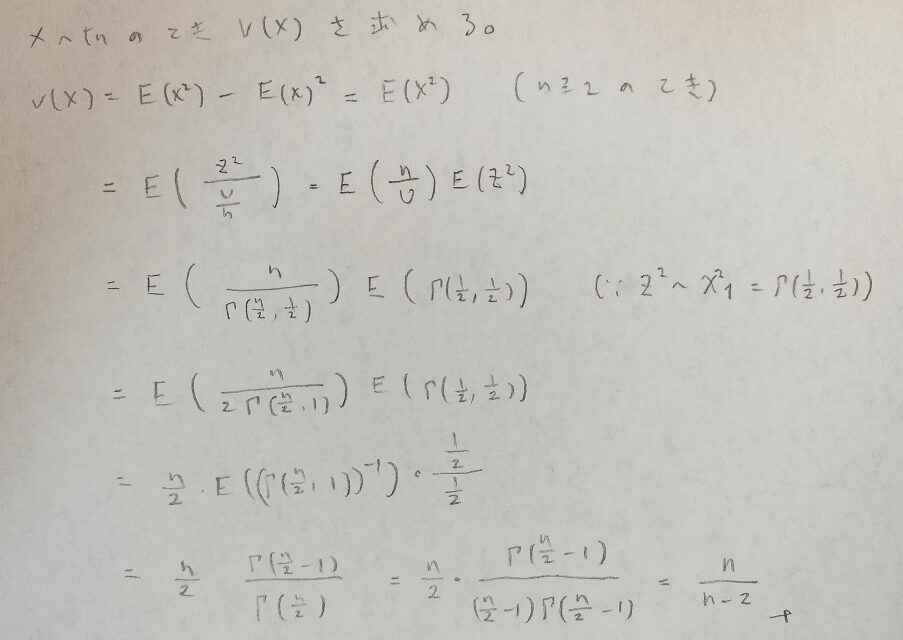
この分散の形は近いうちに「あれ?どっかで見たぞ!」となりますのでお楽しみに!
n=1のときのt分布には期待値が存在しなかったので、当然分散も存在しないのですね。自由度1のt分布だけは特別扱いの分布にしても良さそうです!
標準コーシー分布とコーシー分布には期待値と分散が存在しない
標準コーシー分布
自由度1のt分布の確率密度関数を出してみます!
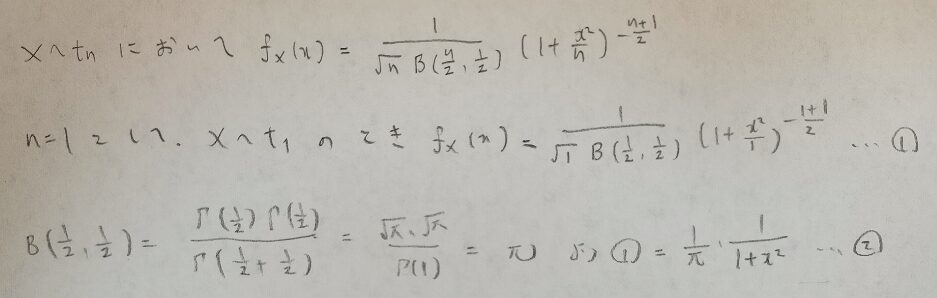
素晴らしい!この②が自由度1のt分布ですね!
πが出てくるのはベータ関数が絡んでいるからで、さらにΓ(1/2)の値の2乗から来ています。そして自由度1のt分布を標準コーシー分布といいC(0,1)という記号で表します。Cは数学者Cauchyの頭文字のCです。Cのパラメータはどのような意味を表すのかは続きをお楽しみください。
自由度1のt分布(つまりC(0,1))に期待値と分散が存在しないことを証明してみます!
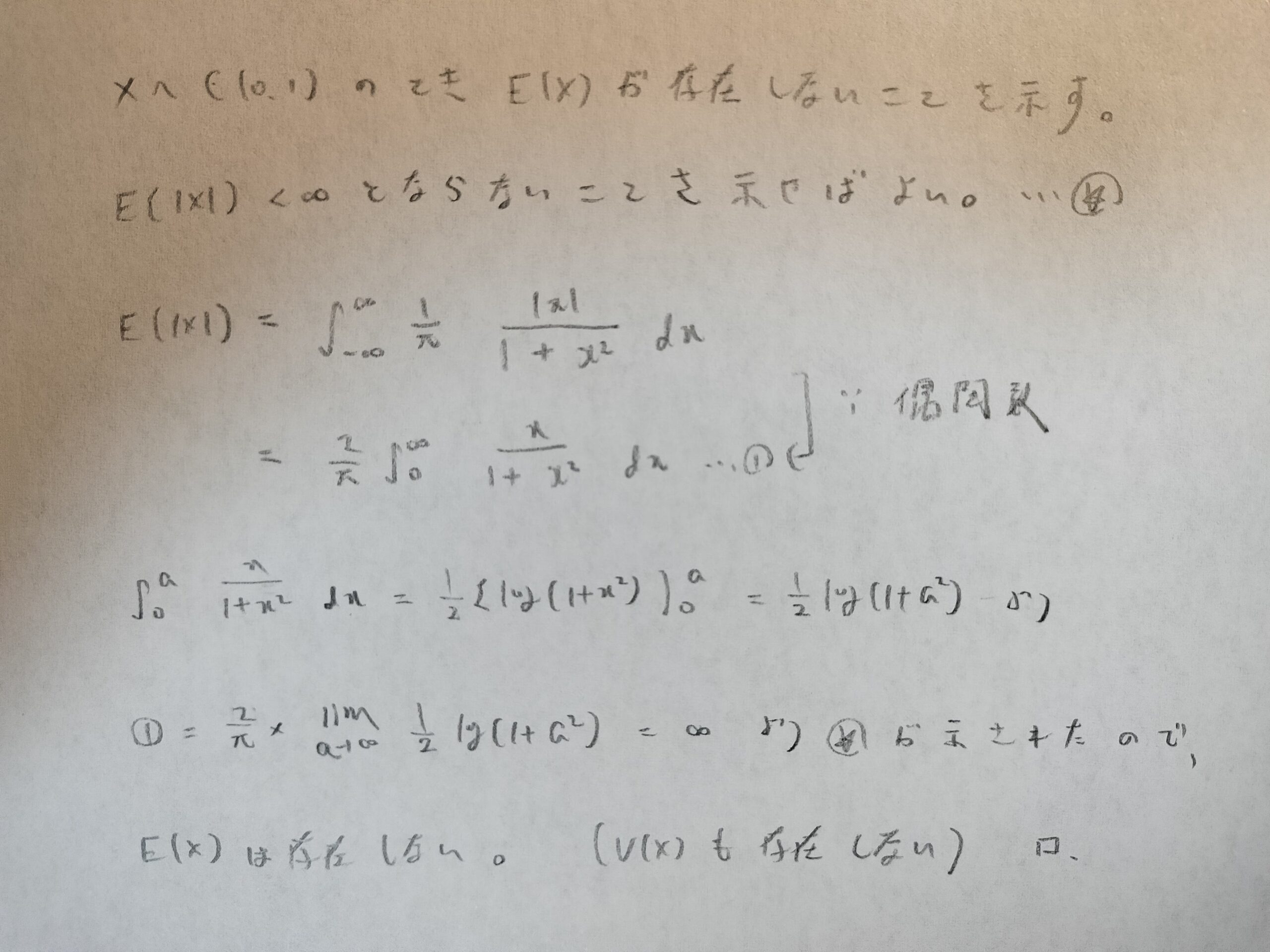
コーシー分布
t分布の自由度を1とした特例が標準コーシー分布でした。今度は標準コーシー分布のパラメータを一般化してみましょう!
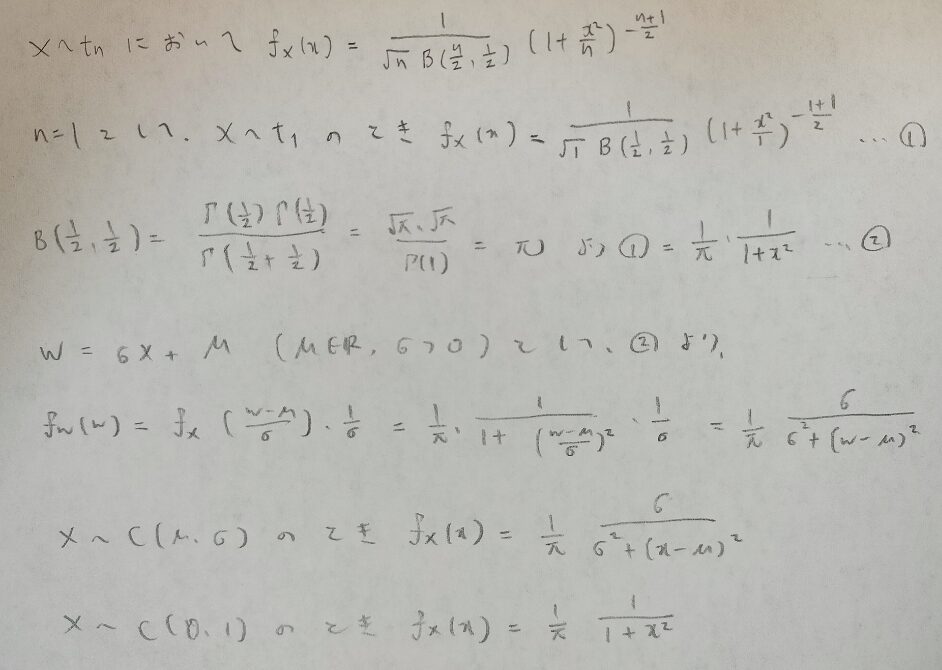
コーシー分布の確率密度関数と標準コーシー分布の確率密度関数をまとめます。
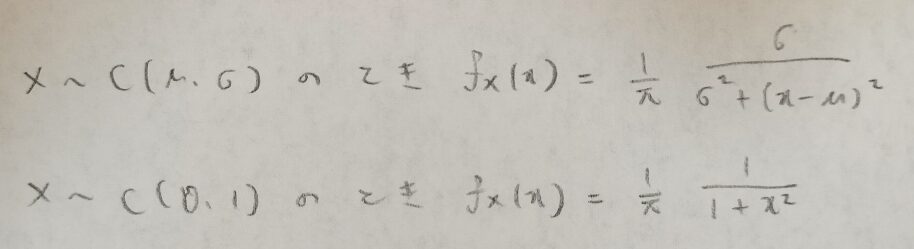
コーシー分布C(μ,σ)のパラメータは期待値と分散を表すわけではありません!
t分布とコーシー分布と正規分布の関係と違い
t分布は正規分布と似ているというか関係してそうだなと思いました。
t分布は正規分布と比べると裾の厚い分布です。特に自由度1のt分布は裾が厚いので期待値がないわけです。『確率統計キャンパス・ゼミ』にはt分布の自由度を大きくしていくと裾が薄くなる過程がわかりやすく示されています。
この記事の最後に正規分布との関係を2つ紹介します。
標準正規分布と標準コーシー分布の関係を計算
標準正規分布の商は標準コーシー分布になります。
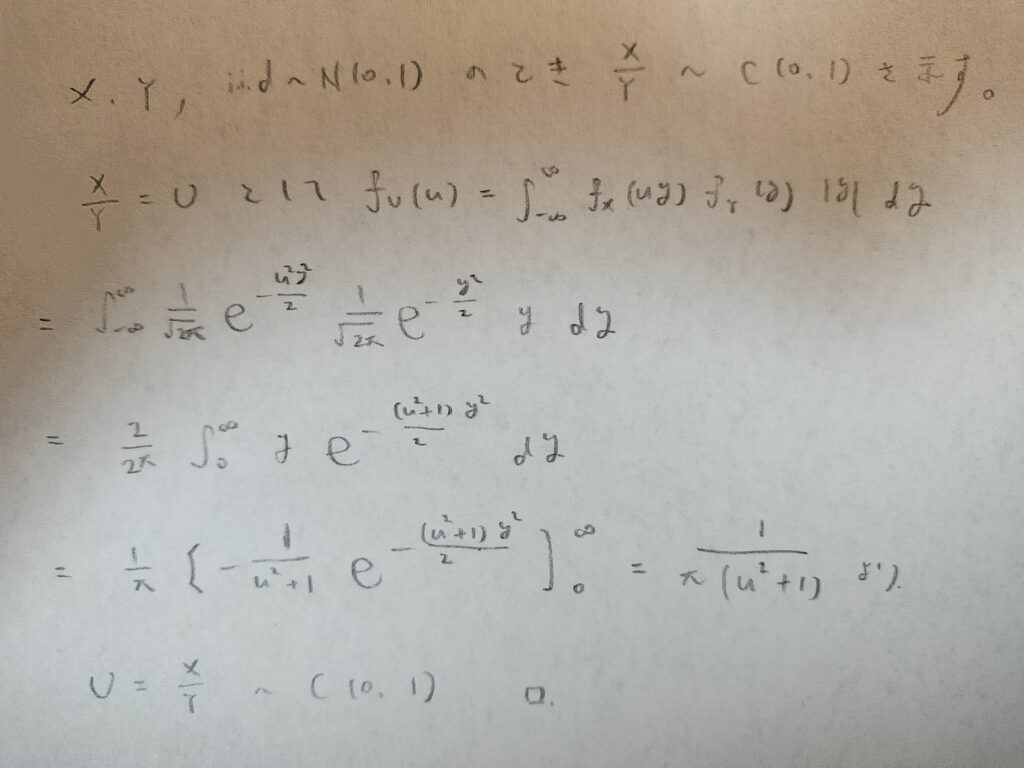
自由度無限のt分布が標準正規分布
t分布の自由度を無限にしたものが標準正規分布になります。
この証明にはスターリングの公式を用います!スターリングの公式に注目をして証明をご覧ください!
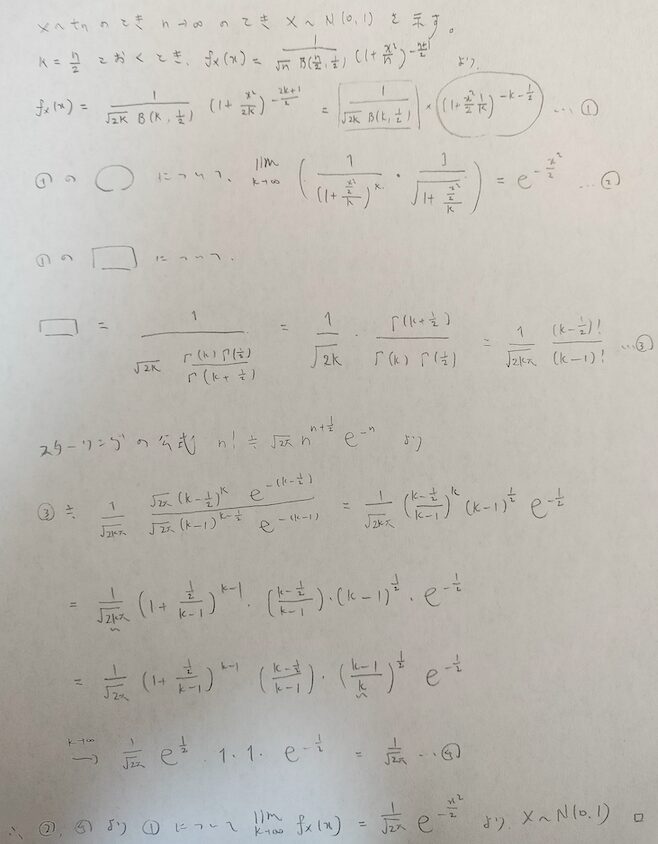
t分布と正規分布の関係性を知って感動しました!
やはり標準正規分布とt分布は似ていました。ゴセットはそのことに気づいて、スチューデント化という概念が考え出されたわけです。(『統計学大百科事典 仕事で使う公式・定理・ルール113』を参考)ゴセットは推定において、母集団の分散が既知の場合は標準正規分布を用いて、分散が未知の場合は標本分散(不偏分散の定数倍)を持ち出せることを示してくれた偉大な方です。