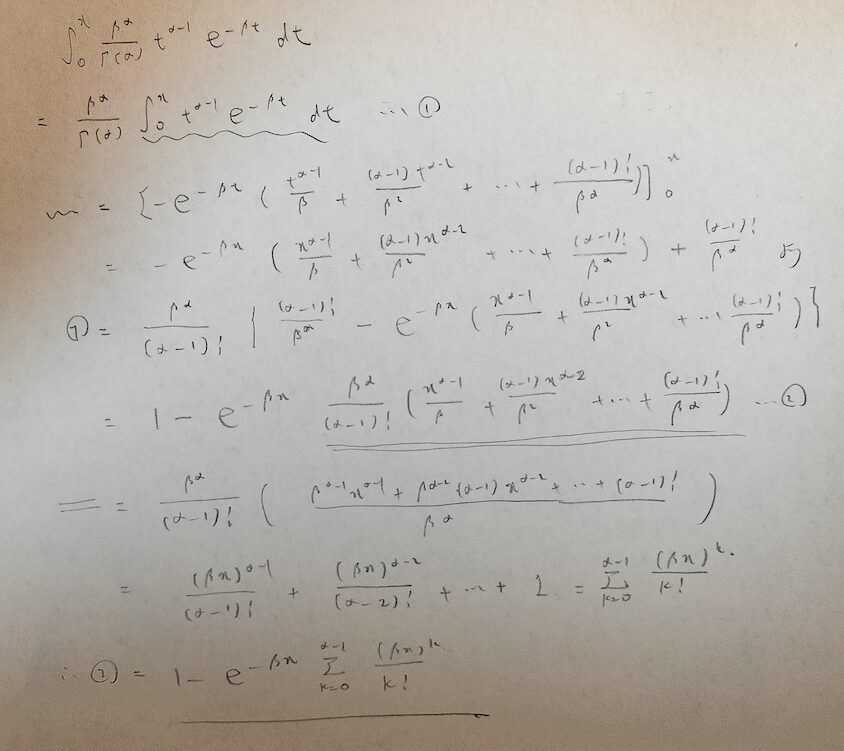いよいよ正規分布を解説します。正規分布は中心極限定理のため確率分布の王だと思っています。
統計学に馴染みがない方でもグラフの形自体はどこかで目にしたことがある有名な分布ですね。
正規分布が絡む計算はガンマ分布の記事で紹介したNO1公式を用いる機会が多いです。ガンマ分布の記事を未読の方はそちらのチェックからおすすめします。
エクセルでも用いられる正規分布は二項分布から導出される
正規分布はパチンコをやる方はゴルトン・ボードという知識(『統計学大百科事典 仕事で使う公式・定理・ルール113』を参照)をご存知かも知れません。このように正規分布は日常にまぎれこんでいます。
これは正規分布が成功か失敗かという原始的な考えから作られる二項分布からの派生系であることが理由です。
正規分布は二項分布においてp(成功確率)を一定としたときにnを無限大にしたときの極限分布として導出されます。正規分布は数学者ガウスの名前にちなんでガウス分布と呼ばれることもあります。
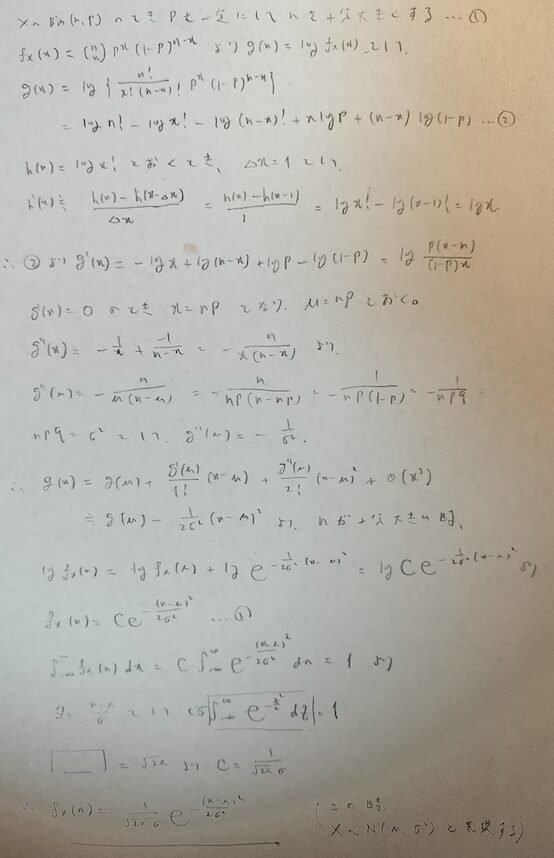
この導出は『確率統計キャンパス・ゼミ』を参考にしました。
この導出ではいくつかの注目する重要なポイントがあります。
①階乗が出てくること→記事後半でスターリングの公式を証明します。
②μとσの2乗の記号が出てくること→どのような意味を持っているのか。
③□で囲った積分計算はどう計算するのか?→ガウス積分をします。
④xをzで置き換えるところは確率変数の標準化を行なっています。
⑤テイラー展開が導出の要として出てくる→中心極限定理の証明でも登場します。
ガウス積分について教えてください。
一般の形で紹介します。
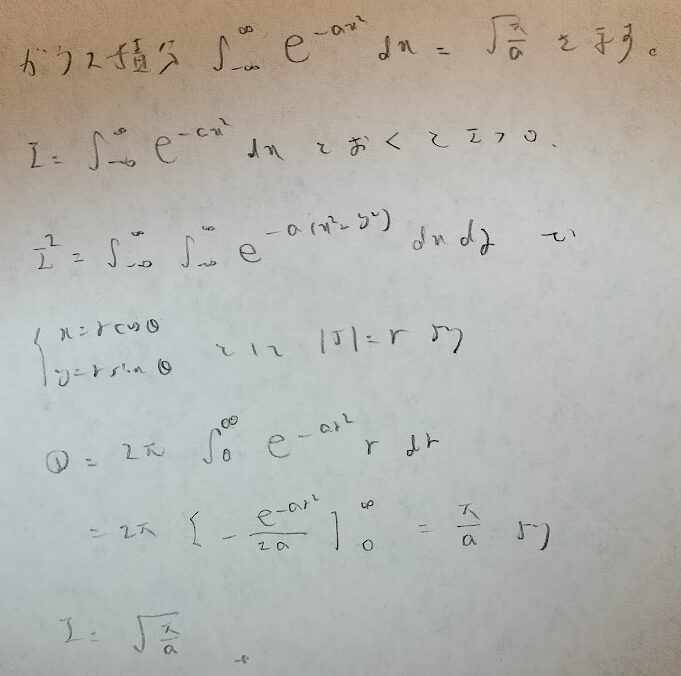
この一般の形は『明解演習 数理統計』を参考にしました。
第1パラメータと第2パラメータを下図のようにしたN(0,1)を標準正規分布といいます。
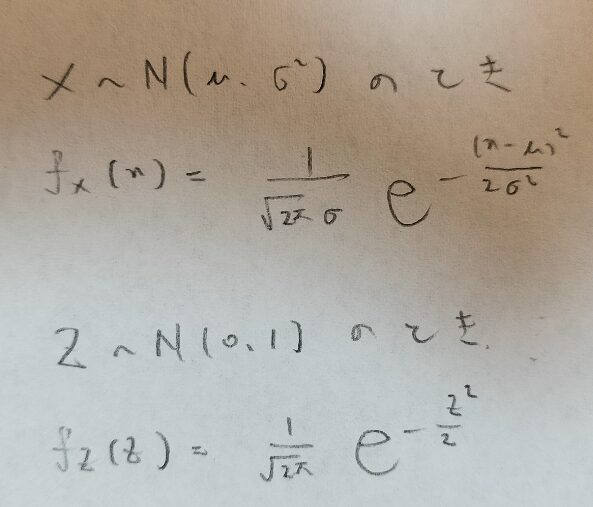
標準正規分布の分布関数は複雑な形ですが利用頻度が多いため、Φ(x)という記号で表します。正規分布の確率密度関数は、φ(x)という記号で表します。これらはギリシャ文字のファイの大文字と小文字です。
正規分布の期待値と分散と標準偏差の導出と積率母関数の計算
X~N(μ,σの2乗)のときのμやσはどのような意味を持っているのですか?
正規分布の期待値と分散を求めていくことで疑問は解決します。
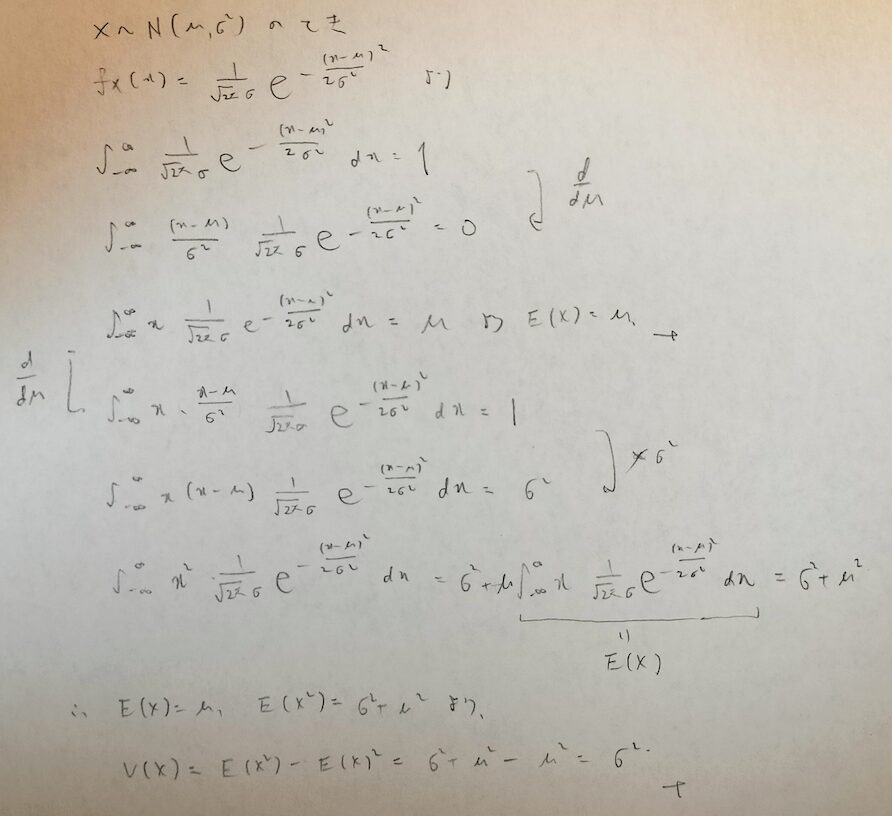
正規分布の全確率1から期待値と分散を導く方法は『データ解析のための数理統計入門』を参考にしました。
正規分布の第1パラメータと第2パラメータはそれぞれ期待値と分散を表しています。つまり標準偏差はσです。
正規分布の積率母関数を求めておきます。
標準正規分布の積率母関数を求めてから変数変換X=σZ+μを用いてXの従う積率母関数を求めます。『リスクを知るための確率・統計入門』を参考にしました。
まずは標準正規分布の積率母関数を求めます。
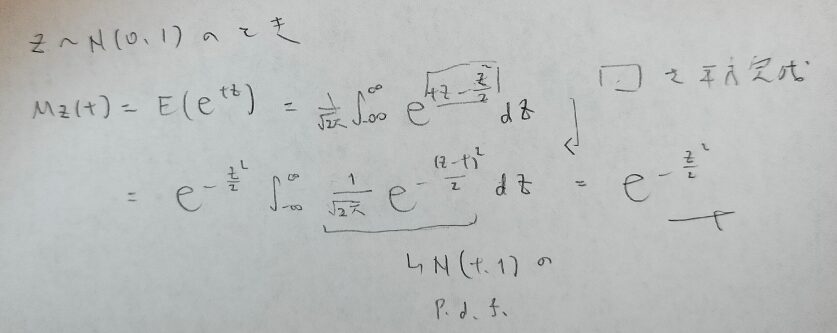
次に変数変換を行い正規分布の積率母関数を求めます。
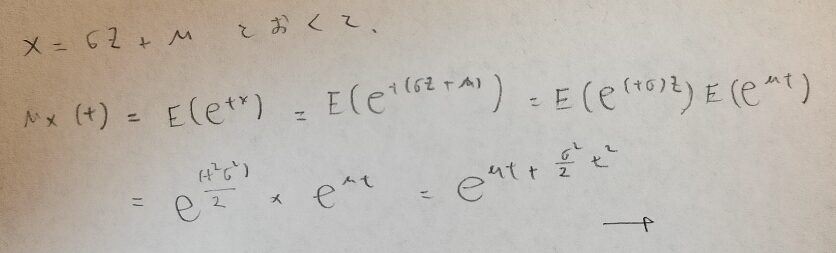
正規分布は再生性がありますか?そしてそれはどちらのパラメータに関しての再生性ですか?
正規分布はどちらのパラメータに関しても再生性を持ちます。ガンマ分布は第1パラメータαについてでしたので、混乱しないように気をつけましょう。
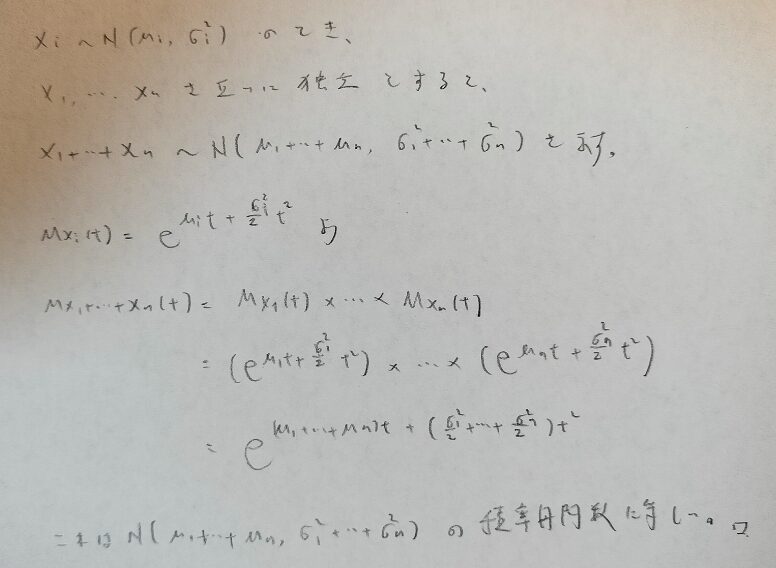
中心極限定理を例題を取り入れてわかりやすく証明します
中心極限定理(central limit theoremを略してCLT)とは下図のようにすれば覚えやすいです。n個の分布は正規分布に従わなくてもOKです。期待値と分散が定まっているという条件があればOKです。『現代数理統計学の基礎』を参考にしました。
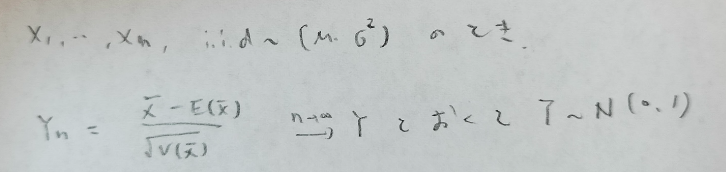
それでは証明します。積率母関数を用いて証明します。ポイントは期待値まわりでのテイラー展開を行うことです。
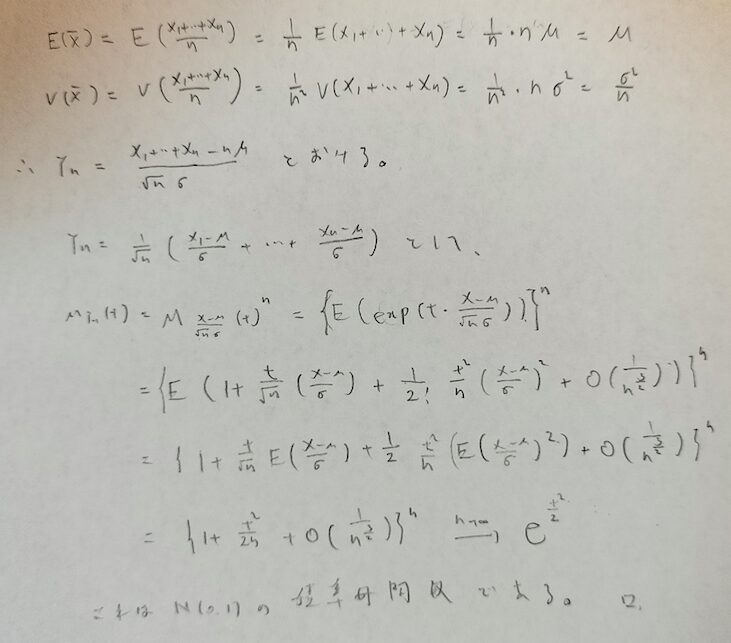
参考書によっては数ページ書いている本もありますよね。それに比べればシンプルな証明で再現しやすいですね。
スターリングの公式を中心極限定理から証明します
nの階乗の近似式であるスターリングの公式を中心極限定理を用いてエレガントに証明します。中心極限定理の例題としてポアソン分布を持ち出しています。
このエレガントな証明は『基本確率 (経済の情報と数理)』を参考にしました。
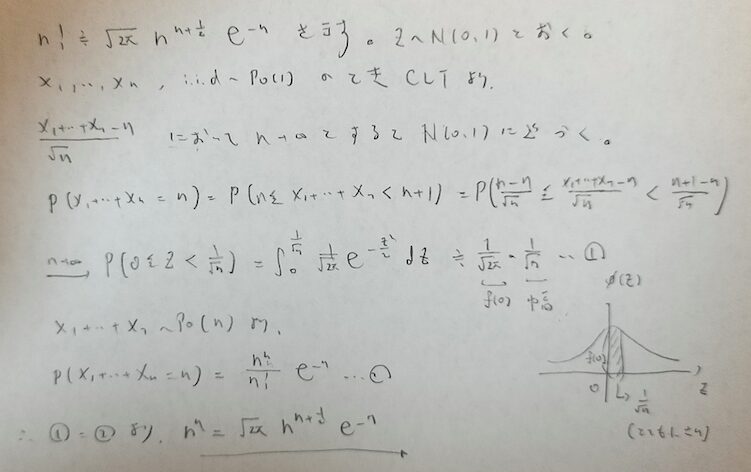
ポアソン分布を持ち出した理由は、期待値と分散が同一なので、うまくnが作れるからなのですね。本当に美しい証明ですね!
標準正規分布の高次モーメントの公式の導出
アクチュアリー数学では標準正規分布の高次モーメントの公式を暗記していないと時間切れになる問題が出題されます。本記事では最後にこれらの公式を導出します。
ガンマ分布の知識が不十分だと計算で時短ができませんのでご注意ください。
まずは絶対値の公式からです。
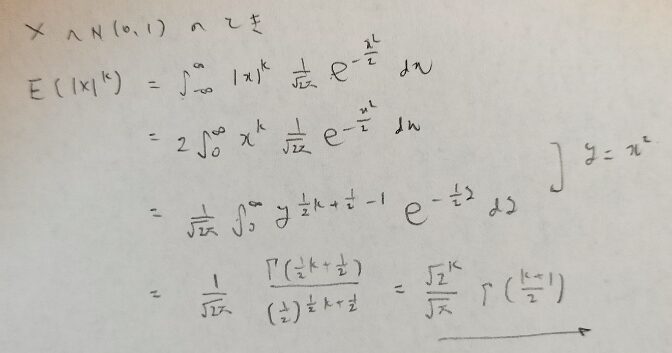
次に有名な公式の証明に行きますが、その前にΓ(1/2)の値が必要になるので計算しておきます。
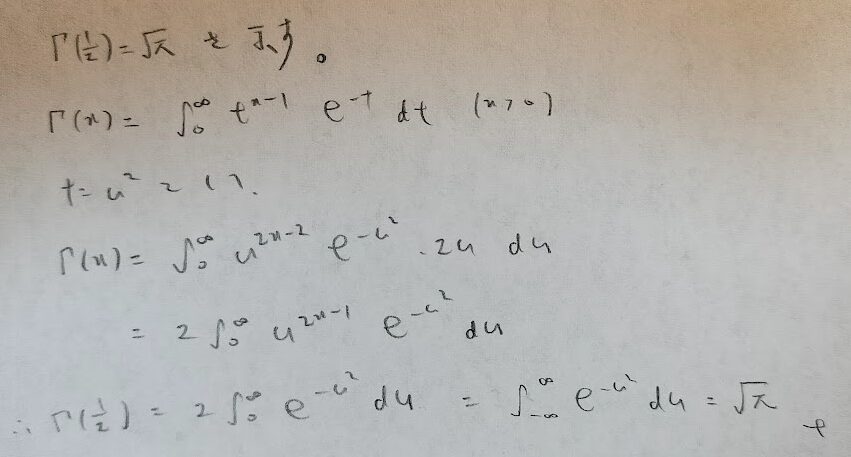
それではいよいよ有名公式の証明にいきます。
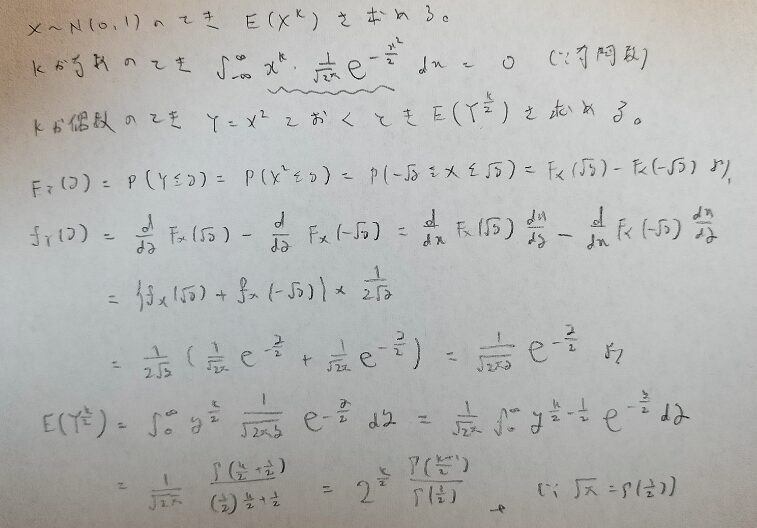
kが偶数の時の公式のメリットが分かりません。
最終結果の式に例えばk=8としてみてください。するとXの8乗の期待値は7・5・3・1と綺麗な結果が得られます。これは7!!とも書けますね。
正規分布には階乗が見え隠れしていたのですね!面白かったです。
最後に標準正規分布と正規分布の記事で参考にした本を紹介します。
正規分布が使われている意外な場面について参考にしました。
二項分布から正規分布を導くところで参考にしました。この導出が載っているのは本書のみです。
アクチュアリー数学でおすすめの教材として紹介される本です。理論と計算テクニックのバランスが素晴らしいです。モデリングは未掲載です。
統計検定1級対策の重要本です。序盤の確率分布の章はエレガントな証明が多めです。
正規分布の積率母関数のところで参考にしました。確率母関数と積率母関数とキュムラントと特性関数の利用場面について詳しい説明があり、かなり重宝しています。
統計検定1級のバイブルです。本書の練習問題のみを周回して統計検定1級に合格された方がいらっしゃるようです。
2023年のアクチュアリーのポーカー問題の大問は本書からのテーマだったと思われます。過去にも同じ問題が出題されたりと知る人ぞ知る、アクチュアリー数学の確率対策の名著です。