統計検定1級の対策書として公式本以外で真っ先に買うべき本である『データ解析のための数理統計入門』の第11章の解説と演習問題を自力で解いた学習の軌跡の記事です。本章は単回帰分析に関する理論の展開となります。ただし最後のクックの距離については難易度が非常に高いため要注意です。演習問題については最後の数問がとても難易度が高いです。
本章では独立性に注意した学習をおすすめします。例えば独立性が保障されない場合に共分散の使用を見流す場合などがありからです。また偏差平方和などの記号は教材や試験問題により異なる場合があります。問題文の通りの記号の使い方を踏襲することをお奨めします。
統計検定1級青本の第11章の説明と例題
本記事では単回帰モデル→推定量の従う分布→正規性の仮定から得られる因果の検定→決定係数→残差分析と誤差項の仮定の確認と改善→個々のデータの影響力の測定の順で論理を展開します。本章も論理性が高いです。
回帰直線を求めて式変形を行います。その際に生じた標本相関係数について深めます。特にデータを標準化した後で求めた回帰係数は元の変数の相関係数と一致します。

次に単回帰モデルを考えます。モデルという言葉が入るので誤差に確率変数を導入します。誤差項における仮定の導入に注意しましょう。ここでは残差についての重要な2つの定理を導きます。それは残差の和が0となること、そして残差とデータとの標本共分散も0となることです。
偏微分を行った式が非常に大事で残差の性質の根本的な箇所に繋がっています。
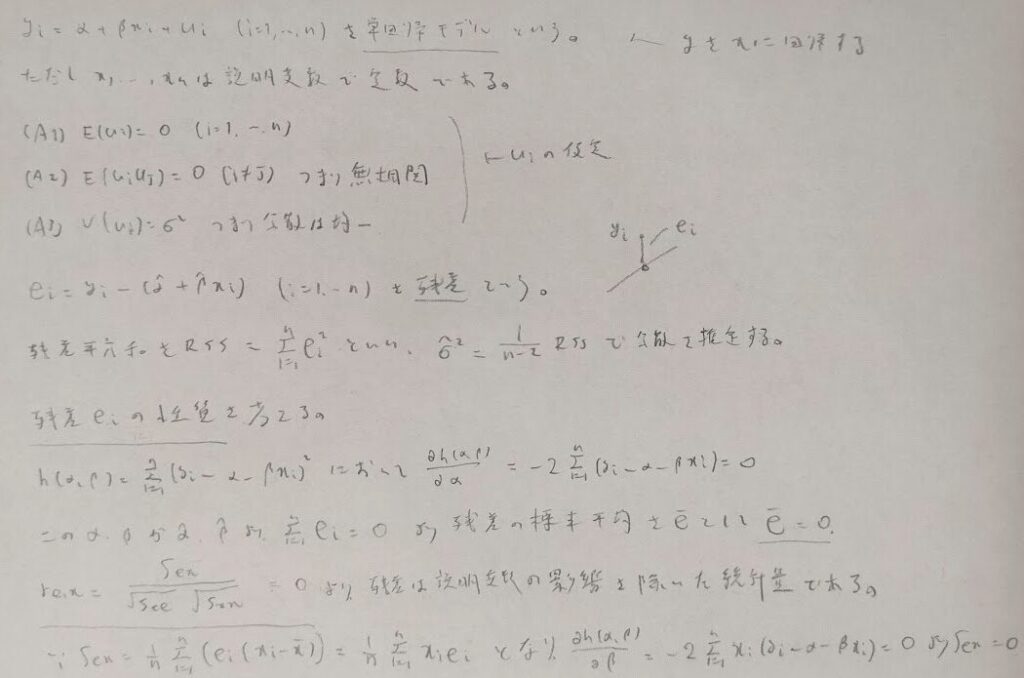
切片の推定値、回帰係数の推定値が従う分布について考察し、誤差の推定にRSS(残差平方和)が出てくる箇所にも言及します。ポイントはこの段階では正規性の仮定がないことです。すなわち一般的な話になります。
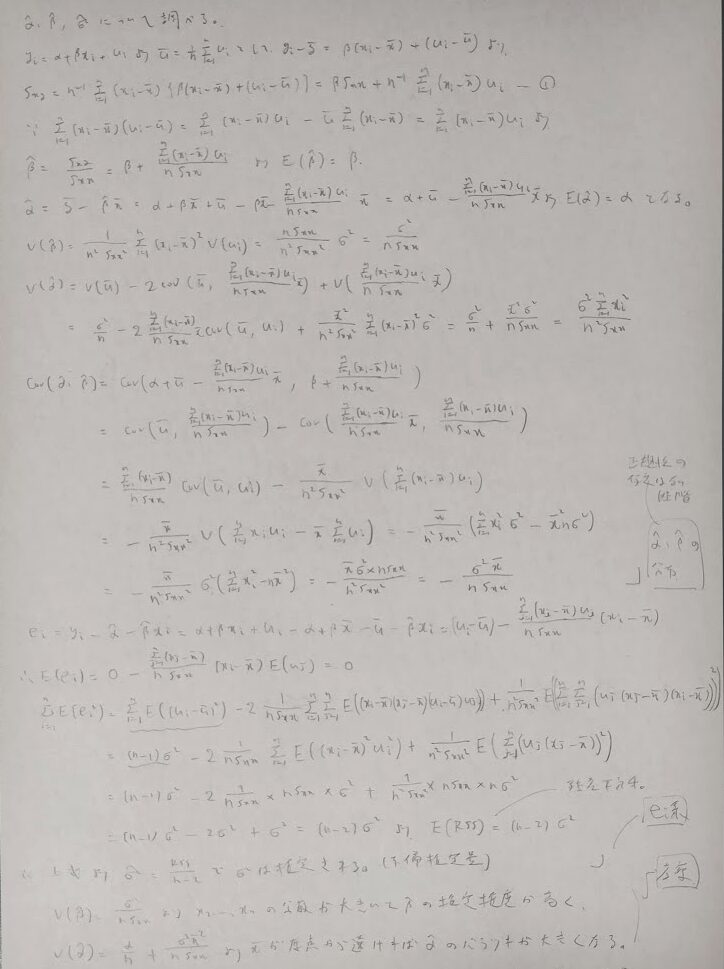
ここまでは誤差項が無相関という性質のみを用いました。ここで無相関と独立が同値になる正規分布の性質を加えます。すなわち正規性の仮定を導入した場合について先ほどの議論の続きを考えます。
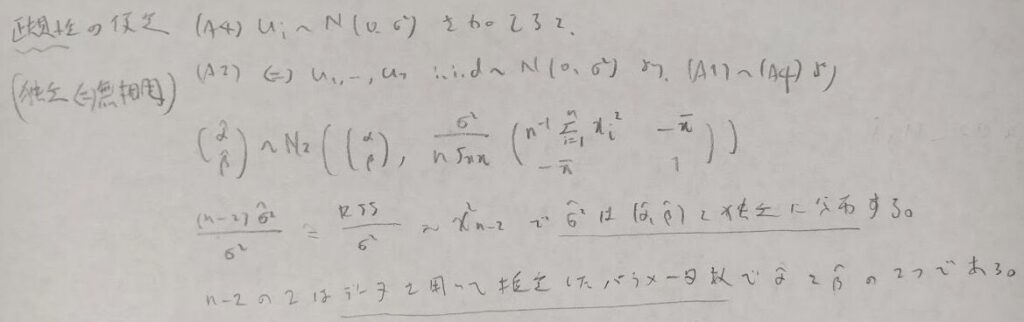
推定量の従う分布が判明したので、仮説検定や信頼区間の議論が可能となります。ここでは変数間に因果があるか?という観点での仮説検定を導入します。信頼区間の話題では、予測誤差に関しても議論が展開できます。
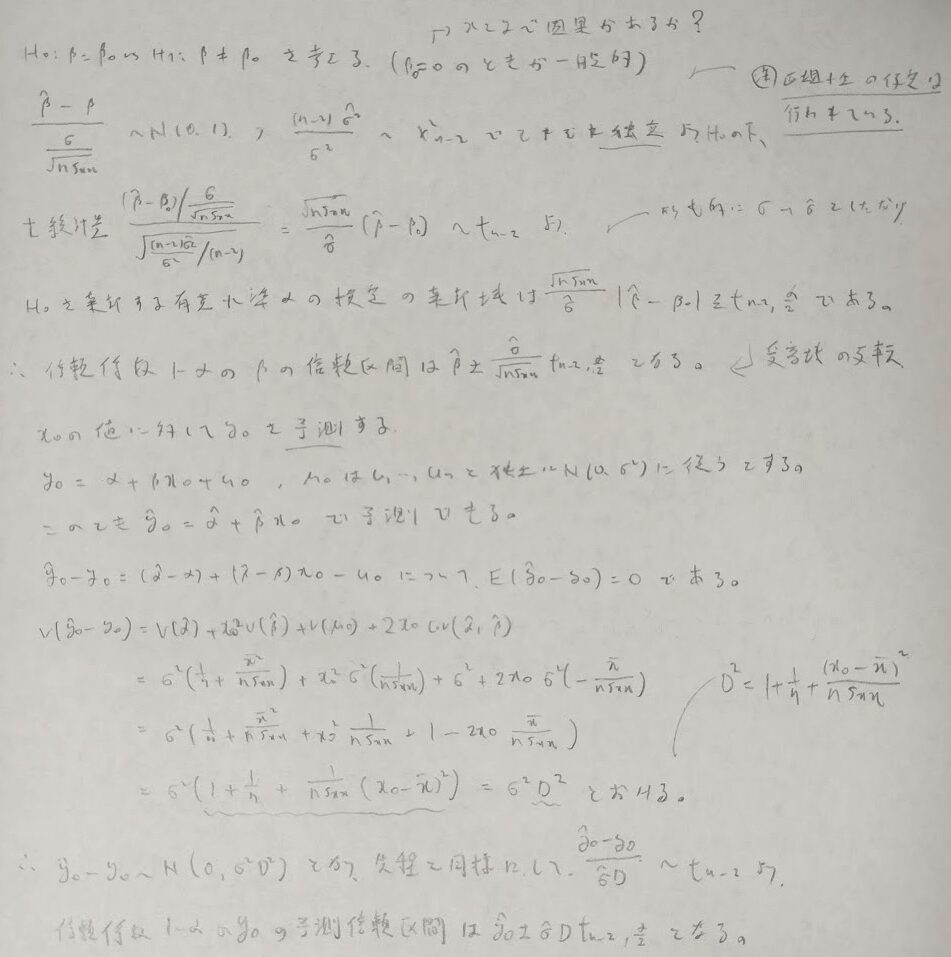
データの予測について外挿は危険です。
データが回帰モデルにどの程度当てはまっているか?を表す決定係数関連の話題に移ります。ヘドニック法とは商品などの価格を説明できる回帰式を求める方法です。決定係数が高いからといってモデルの当て嵌まりが良いと断言することは危険です。判例はアンスコムの例です。
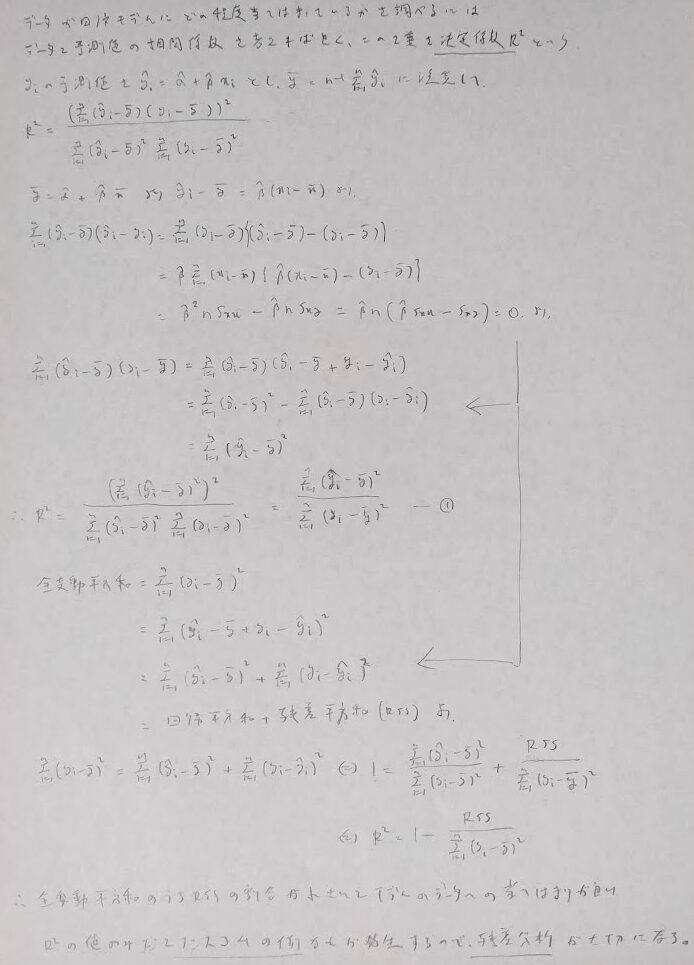
残差分析の方法について学びます。残差プロットに規則性や傾向性がないことが望ましいです。この残差分析では誤差全体の期待値が0になっているはずです。これは(A1)誤差項の期待値が0であることに相当します。

残差プロットで他にわかることはありますか?
誤差項について(A4)正規性の仮定、(A3)分散の均一性、(A2)誤差の無相関性の検討ができます。この順に考察していきます。
分布の正規性について疑わしいことが次の条件から解ります。
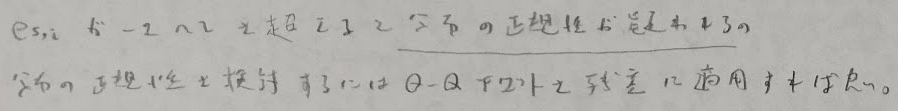
また分布の不均一性についても考えることができます。

系列相関を調べることにより誤差項の無相関性について検討することができます。

最後に個々のデータの影響力について、てこ比とクックの距離を扱います。クックの距離について難易度は単回帰分析においてラスボス的です。
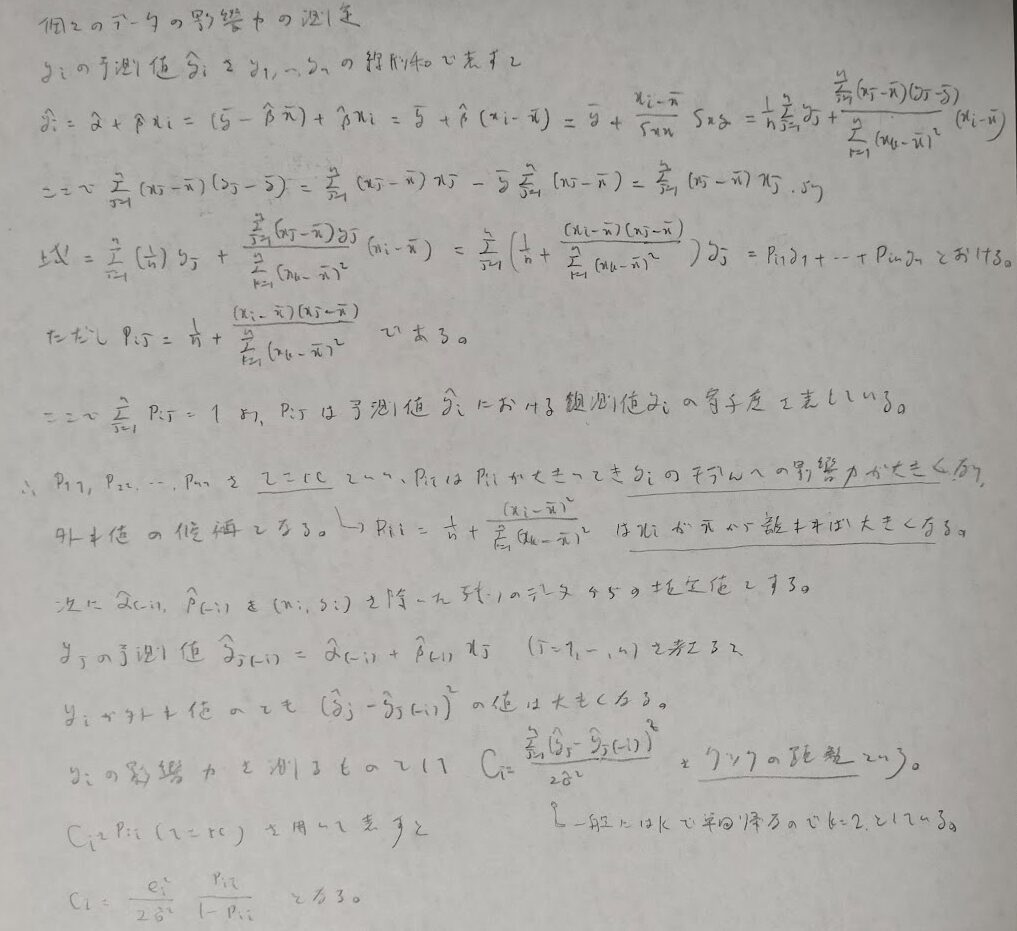
最後の式の分母に2乗を書き忘れました。2乗が正しいです。
統計検定1級青本の第11章の演習問題
中盤から単回帰モデルへの言い換えができるようになるとスムーズに問題が解けるようになります。最後の数問の難易度は非常に難易度が高いです。
問1:Rの分析結果
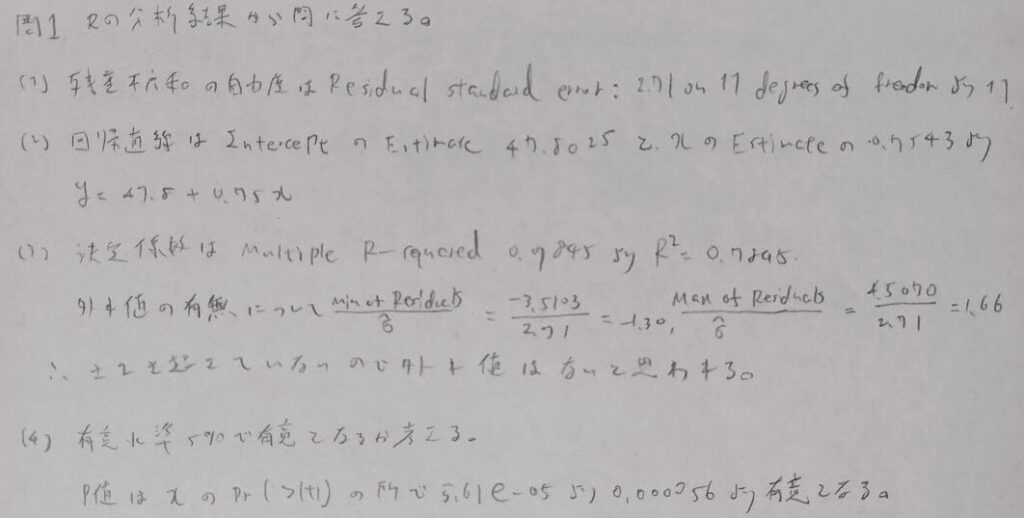
問2:実データ解析
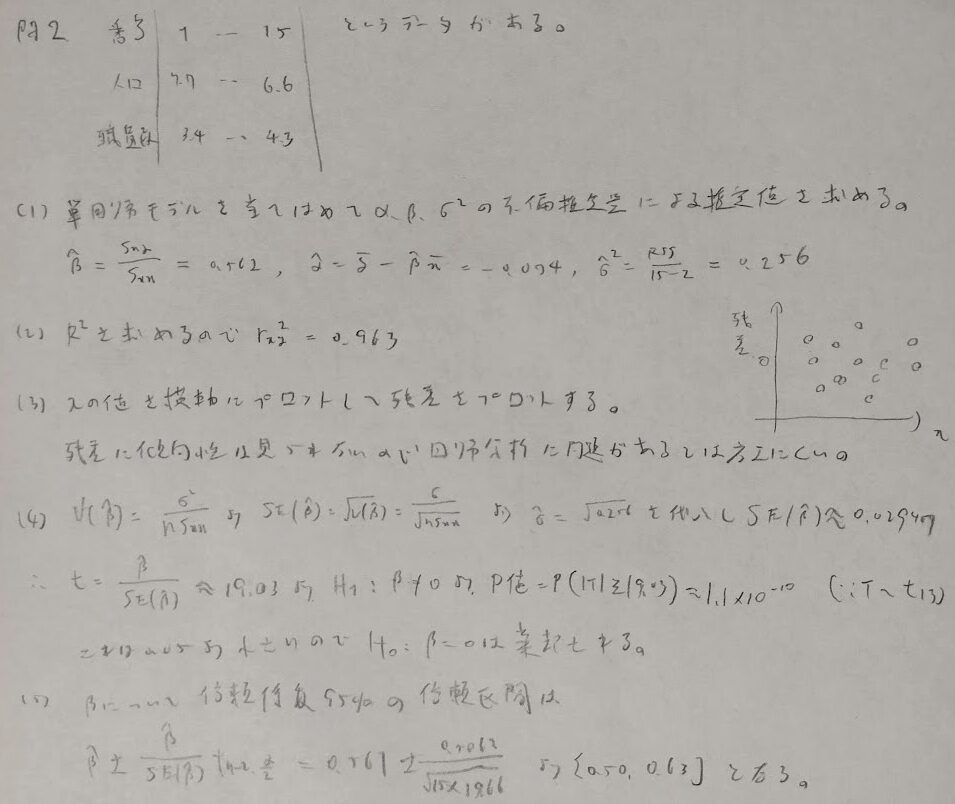
問3:誤差項の仮定の確認と改善

問4は本文のDに関する内容で既に記述済み。
問5:単回帰モデルの式に直さないで回答
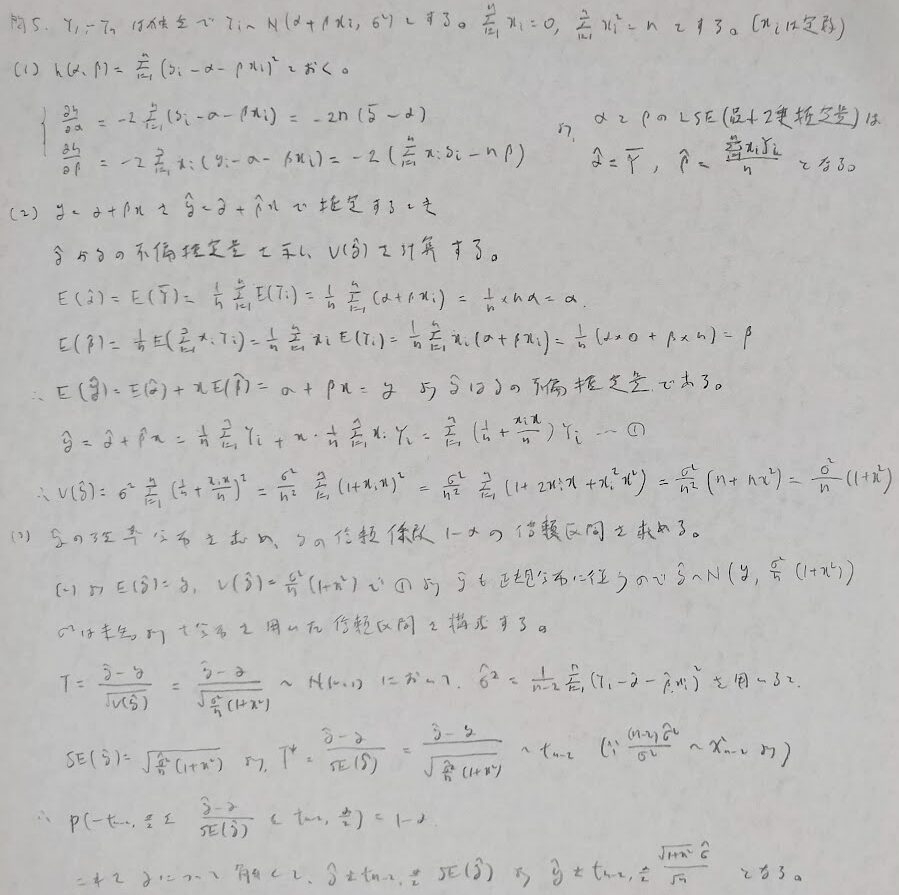
単回帰モデルに直した答案も可能です。問6以降はその方針で考えます。
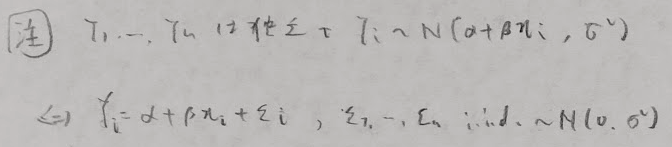
問6:単回帰モデルを用いた答案
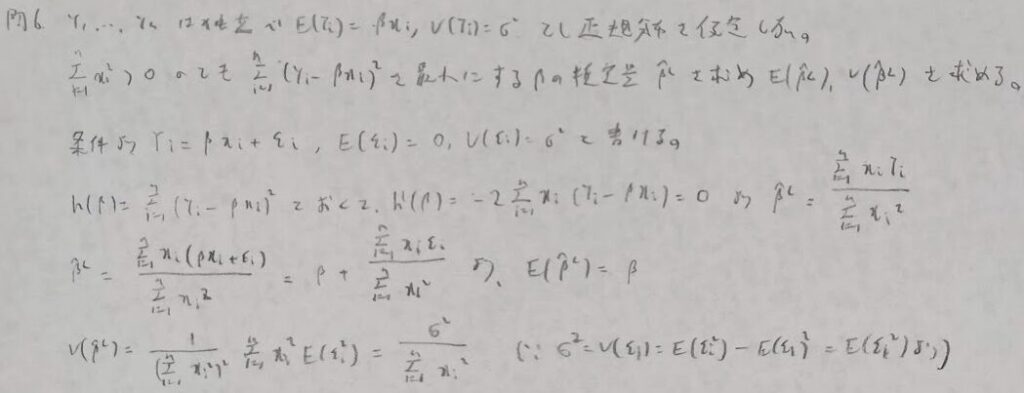
問7:コーシー・シュワルツの不等式との融合

問8:残差平方和の従う分布

問9:本章最難関
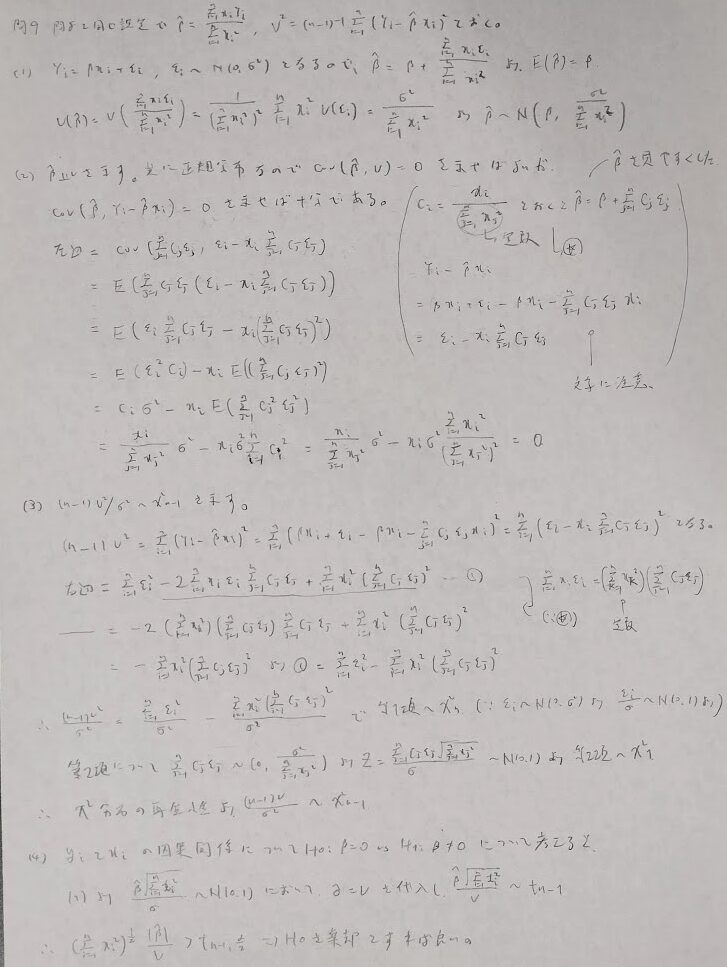
ポイントは(2)で置き換えること、そして(3)でカイ2乗分布の再生性を使おうとする意欲です。非常に難易度が高い問題ですが、とても良い問題だと思います。僕はこの1問を解くだけで2時間使いました。
問10:尤度は大文字を原則使う

問11:母相関係数の検定

単回帰モデルに置き換えることにより導出ができます。アクチュアリー数学2024にも誘導付きで出題された内容です。次は重回帰モデルになります。残差平方和関連の厳密な証明が与えられることになります。