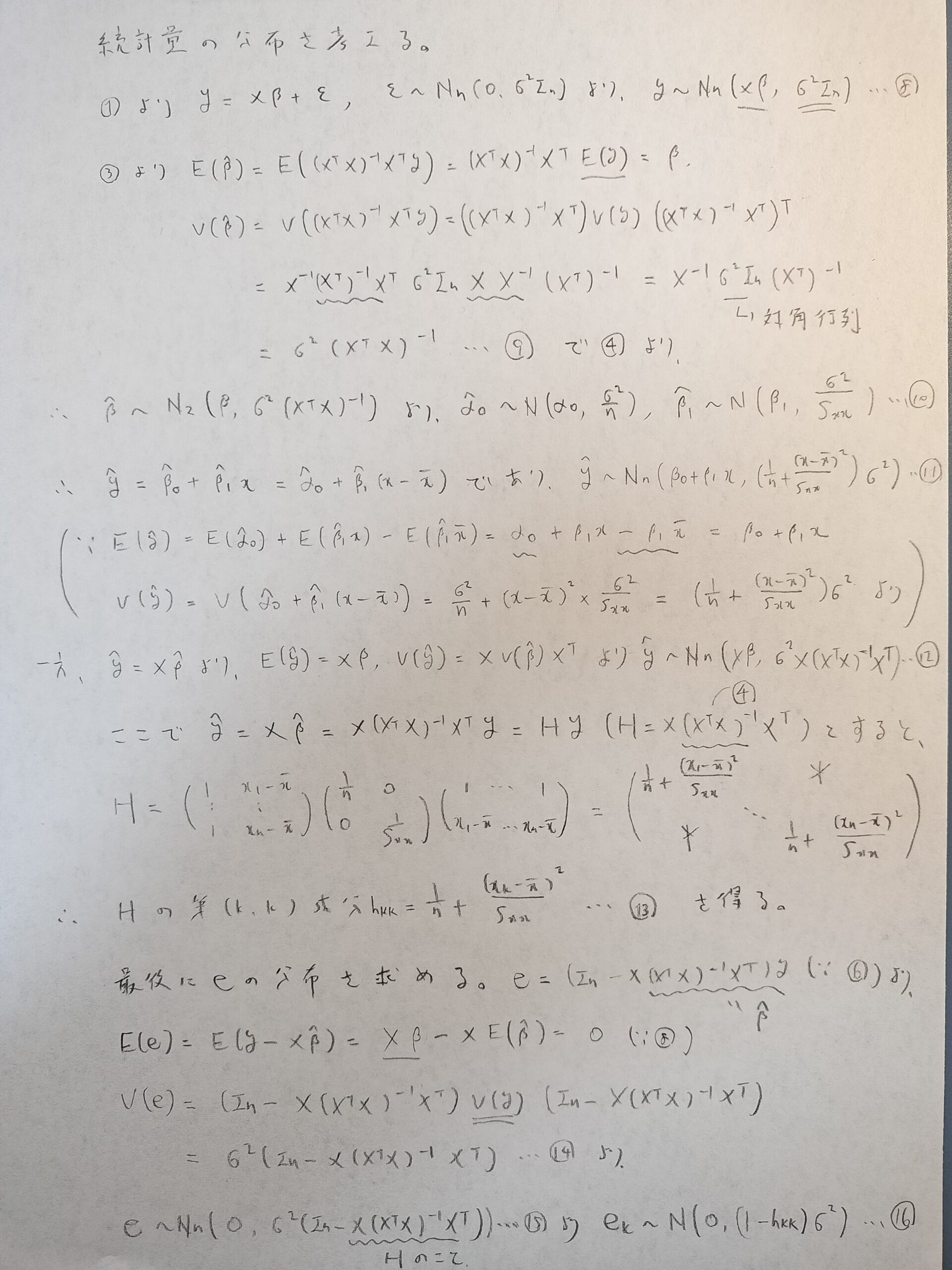多変量解析の話題の第一弾として、単回帰分析を学びます。回帰分析は多変量解析の書籍の始めに登場するものです。多変量解析は色々な種類があり、これらを使いこなせる方は分析が上手い方という認識です。
僕が最初に単回帰分析を知ったのは数学検定1級を受けるために『確率統計キャンパス・ゼミ』で統計を勉強していたときでした。数学検定1級の1次検定でも「回帰直線を求めよ」という問題が出るためです。
単回帰分析はどのような分析手法なのですか?
説明変数xを用いて目的変数yを予測するためのものです。単回帰分析では回帰直線というものを求めて、回帰直線をもとに任意に与えたxに対してyを予測するための手法です。
数学検定1級では基本的に回帰直線を求められれば大丈夫なことが多いですが、統計検定1級やアクチュアリー数学では、さらに深い理解が問われます。この記事では単回帰分析に登場する全ての公式を網羅するためのものです。
単回帰分析そのものが初見の方は『確率統計キャンパス・ゼミ』をご一読なさることをおすすめします。本書は僕が中学3年生の頃に新宿の紀伊國屋で購入しましたが、その年齢でもわかりやすく書かれていたため、内容(回帰直線を出すまで)を理解することができました。入門としておすすめしておきます!
単回帰分析を行列表示するとエクセルでも行える点推定の準備ができる
これから単回帰分析の内容に入っていきますが、前提知識として多変量正規分布の内容を扱います。未習の方はこちらの記事から学習されることをおすすめします。
まずは大まかなストーリーをお話しします。この章での最終目標は残差平方和の最小値を行列表示を用いて求めることです。また、登場する文字が確率変数か否かを意識するようにしてください。
誤差項ε(擾乱項とも言われます)を多変量正規分布に従うようにすることを意識しつつ、行列y、X、β、εを設定します。V(y)とは分散共分散行列のことで、各εは互いに独立なので、分散共分散行列は対角行列になります。
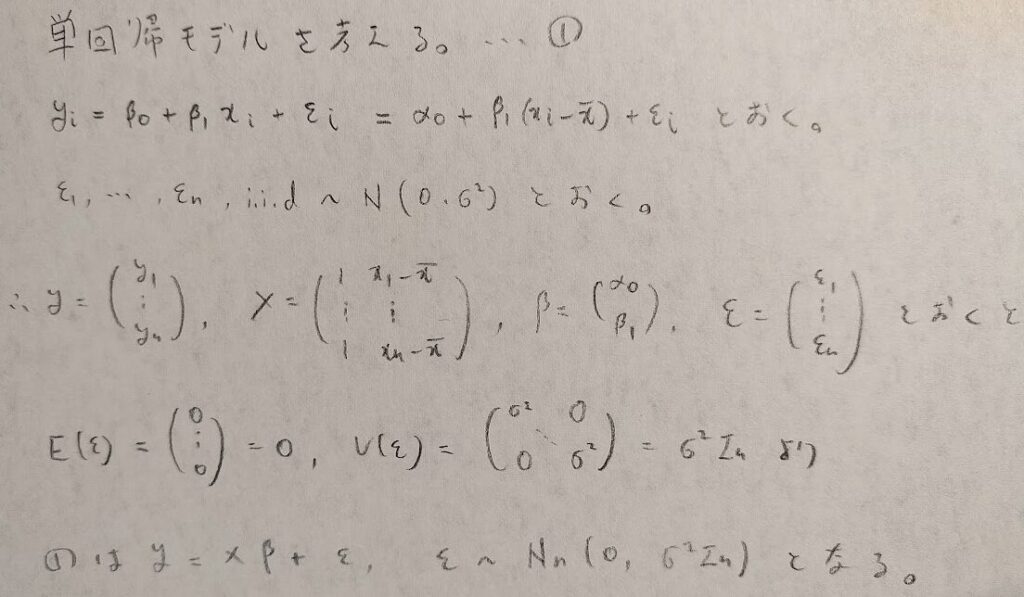
①の下の式の中辺と右辺はそれぞれ役割があります。そこに注意して式変形を追ってください!
次は残差ベクトルeを設定していきます。y ^(←yハットと呼びます)は予測値ベクトルです。残差とは実際の値のyから予測値y ^の差を表します。そして残差平方和は残差の2乗和で定義されます。
SeやSxxなど、二乗和関連がSを用いて表現されます。標本分散などで同じ記号を用いると紛らわしいことから、難しい統計学を意識している書籍では、標本分散をVxなどのVという記号を用いて表します。
行っている計算はシンプルです。残差平方和を求めて、それを変数であるβ^で偏微分しているだけです。ただし行列の微分方法には注意です。
数学検定1級の線形代数で勉強した二次形式のお話で1変数の2乗を転値行列を用いた行列表現でできることを学びました。図02を見てもパッとしない方はを『線形代数キャンパス・ゼミ』ご覧ください。最短コースで理解できます。
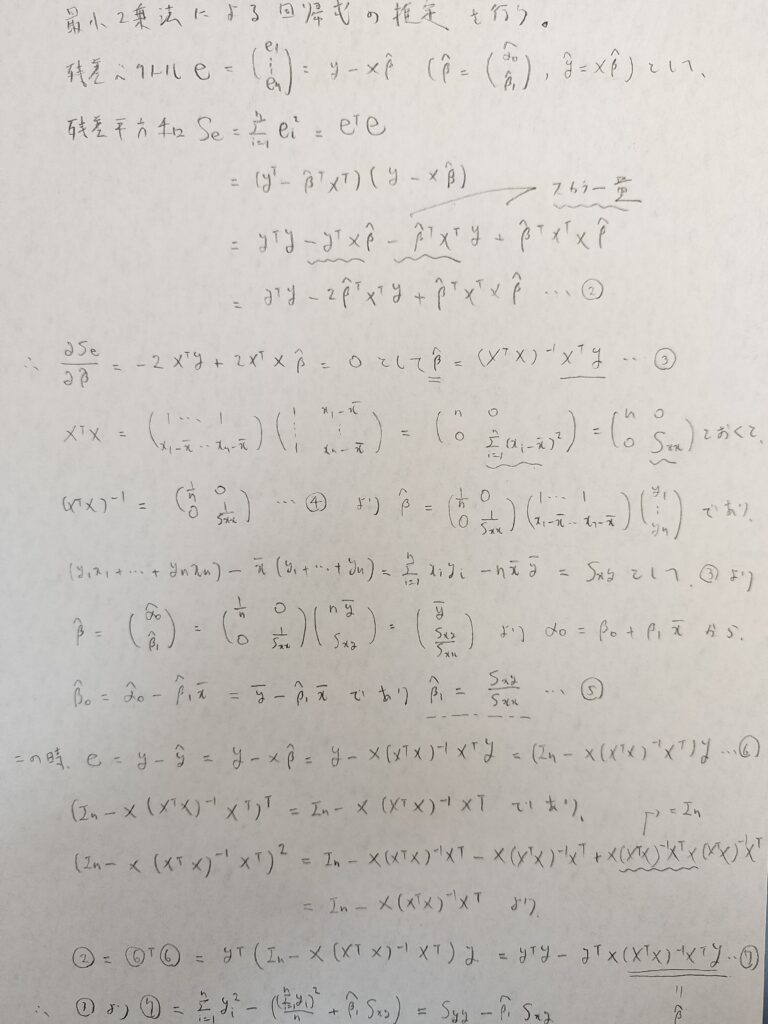
⑥式のyの係数の行列はよく出てくる行列です。この行列は転置をしても変わらず、2乗をしても変わらない行列です。図02の終盤ではこのことを証明しています。この内容を知っていればもっと簡潔に結論まで辿り着けます。
⑤でβの推定量を求めており、⑦で残差平方和の最小値を求めたことになります。
しかしこれだけでは、これらの値の点推定しかできないため、区間推定や検定を行えるようにするために、統計量が従う分布を求めていく必要性が出てきます。
単回帰分析の統計量の分布を求めてp値を出せるようにする
ここでの目標はyやβ^やy ^や残差eの従う分布を求めていくことです。
予測値ベクトルy ^は前章での注意でもありました通り、2通りの求め方からなる結果(量的には同じですが、表現方法が異なります)を導きます。これらの結果は記事の後半にて必要になります。
多変量正規分布か正規分布か、どちらに従うのかは行列の成分の数に注目すればわかります。例えば成分の数が25ならば5変量正規分布に従うことになります。
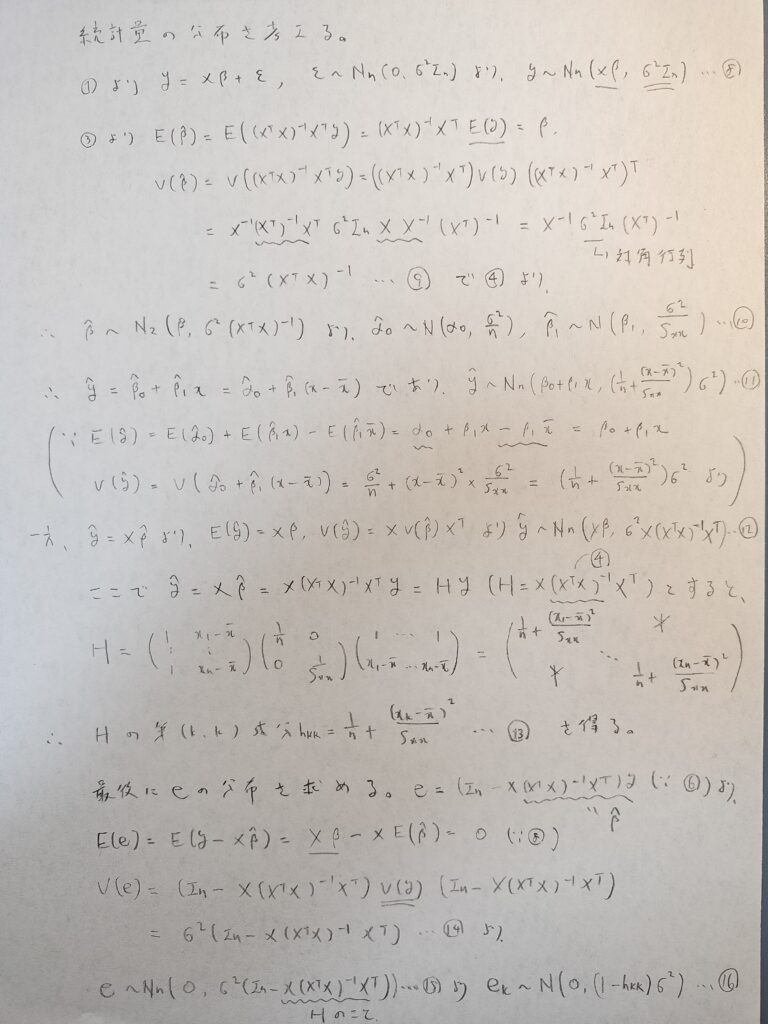
④の式で定義されるHをハット行列といい、予測値ベクトルと目的変数とを結びつける大事な行列です。単回帰分析の深いところでは、図03の13番の式や最終行の16番の式のように、Hの対角成分が重要な役割を担います。
これで行列表示になる単回帰分析の説明はすべて終了です。お疲れ様でした!
次は、行列表示を行なって得られた他の式の結果から、単回帰分析の重要な性質を追っていきましょう!
単回帰分析の自由度を考えて決定係数の正体である寄与率を調べる
アクチュアリー数学や統計検定1級で頻出の決定係数について、その意味を調べていきます。そのためには自由度という概念が必要になりますので、自由度について解説します。この内容は分散分析の入り口に触れる内容になります。自由度をφという記号で表していきます。
全変動の平方和の分解
図04の1業目の式を全変動といいます。まずはこの式の平方和を分解します。この考えは統計学全般にわたって大事な考えです。
イメージ的には三平方の定理に近いです。
図04の下から2行目の式は全変動=回帰変動+残差変動(残差平方和のことです)に分けられると言っています。回帰変動のことを回帰による平方和ということもあります。
回帰変動ってどういう意味ですか?
データの変動(全変動)のうちで回帰直線によって説明できる部分のことです。実際に回帰変動はyの予測値ベクトルからyの平均値を引いたものです。yの平均値は回帰直線上にありますから、回帰変動は回帰直線によって説明できる部分を意味しています。
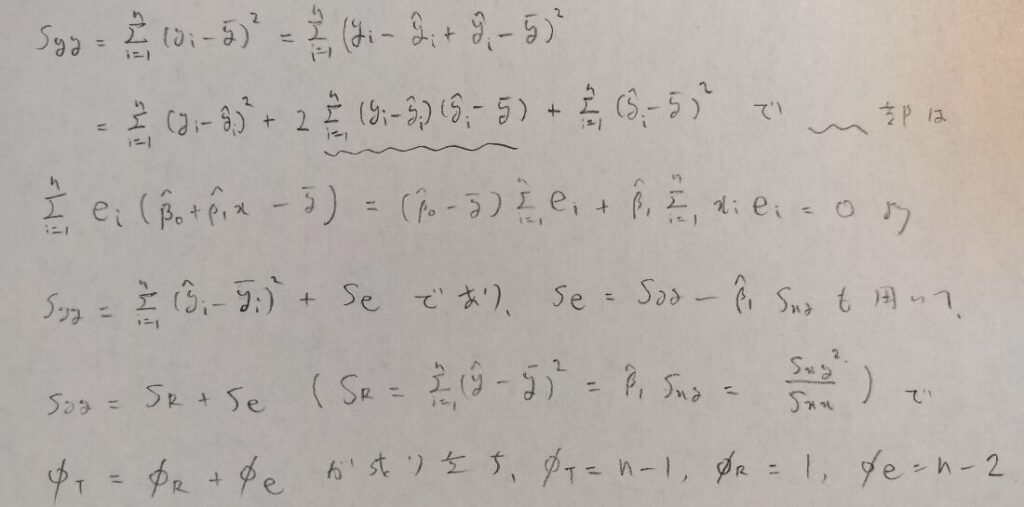
平方和の分解を行うと、自由度に関する等式を得ることができます。この場合は残差変動の自由度がn-2となることに注意しましょう。
各自由度がなかなか覚えられません。コツを教えてください。
まずは全平方和の自由度は、yの平均値を決めていることからn-1になります。残差変動は、次の図05の2つの式の制約があるためn-2となります。最後の回帰変動の自由度は、平方和の分解の結果から、ただちに1と求まります。
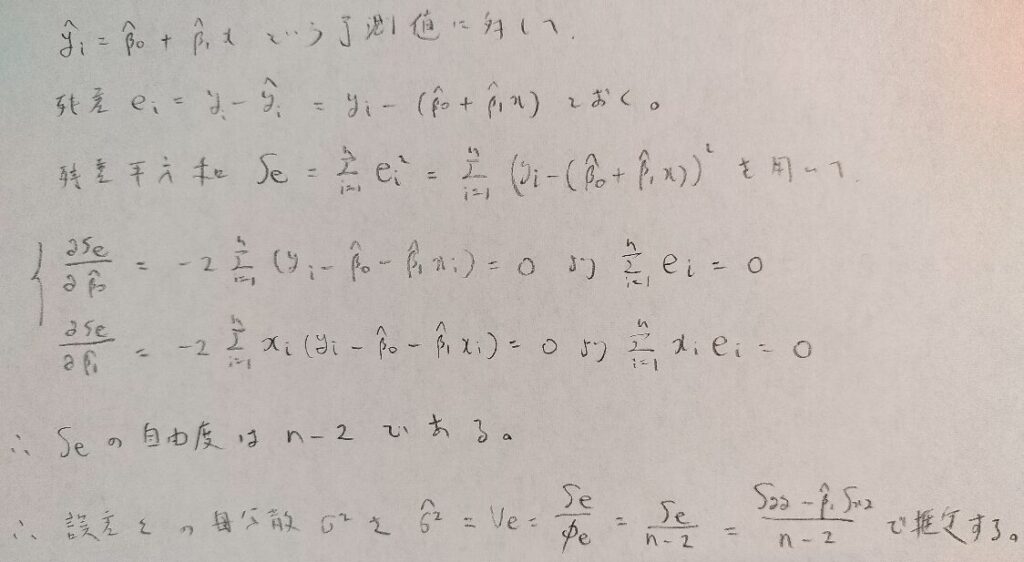
図05は初歩の時に学習した方法でしたね。この中に残差変動の自由度の鍵が隠されていたのですね。驚きです!
推定値の平方根を、推定値の標準誤差と呼びます。標準誤差が小さいほど、回帰式がよく適合していると判断できます。
決定係数の正体
いよいよ決定係数に入ります。
決定係数とは全変動のうち回帰によって説明できる変動の割合として定義されます。
この定義を数式化すると自然と決定係数(他の多変量解析との整合性も考えると寄与率ということがあります)が導かれます。
決定係数が大きいほど、「回帰式がデータによく当てはまっている」と言えるのですね!面白い。
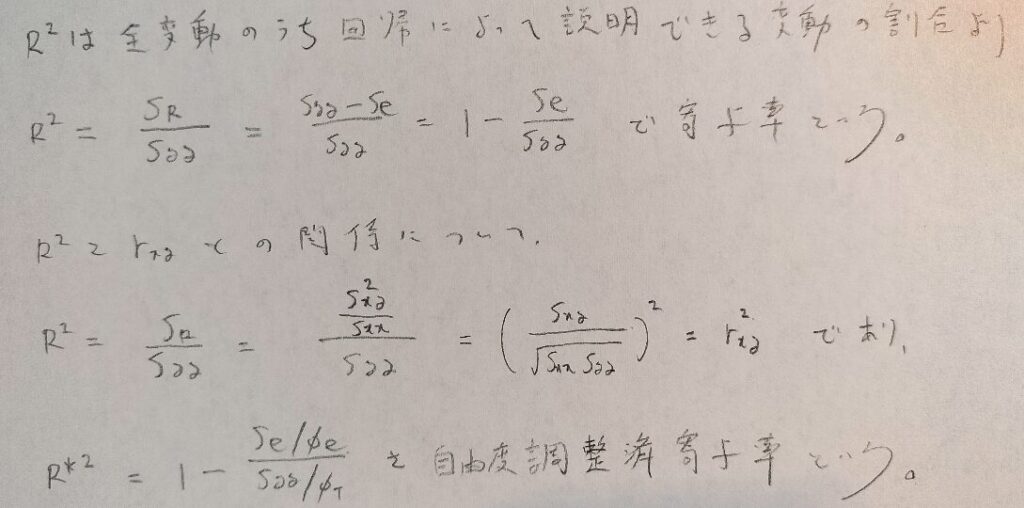
決定係数は相関係数の2乗という綺麗な結果が得られたので、万能感があるかも知れません。しかし欠点もあります。
重回帰分析になって説明変数が増加すると、必ず決定係数が増加してしまいます。そのことを考慮した決定係数を、自由度調整済決定係数(自由度調整済寄与率)といいます。
テコ比の意味
行列を用いた説明で登場したハット行列Hの対角成分の意味が、ここでやっとわかります。図07の1行目のテコ比について、これはxの平均からのk番目のxの離れ具合を表す式です。つまりテコ比が大きいほど、n個のy予測値のうちのk番目が、k番目の実測値であるyの変動を大きく受けることになり、好ましくはありません。
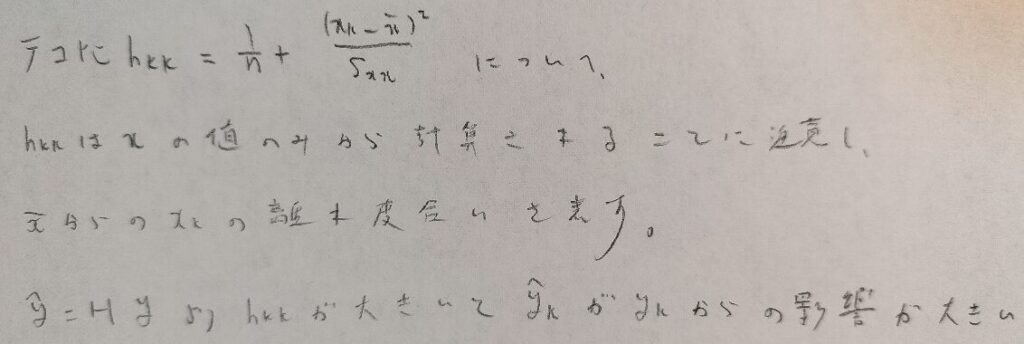
単回帰分析では、回帰直線を書き込めば様子がわかることに対し、重回帰分析ではそうはいきません。このような時にでも使える理論としてテコ比を導入しておくのです。
テコ比を用いた解析法は他にはありますか?
あります。そのためにはテコ比の取りうる範囲を出しておく必要があります。
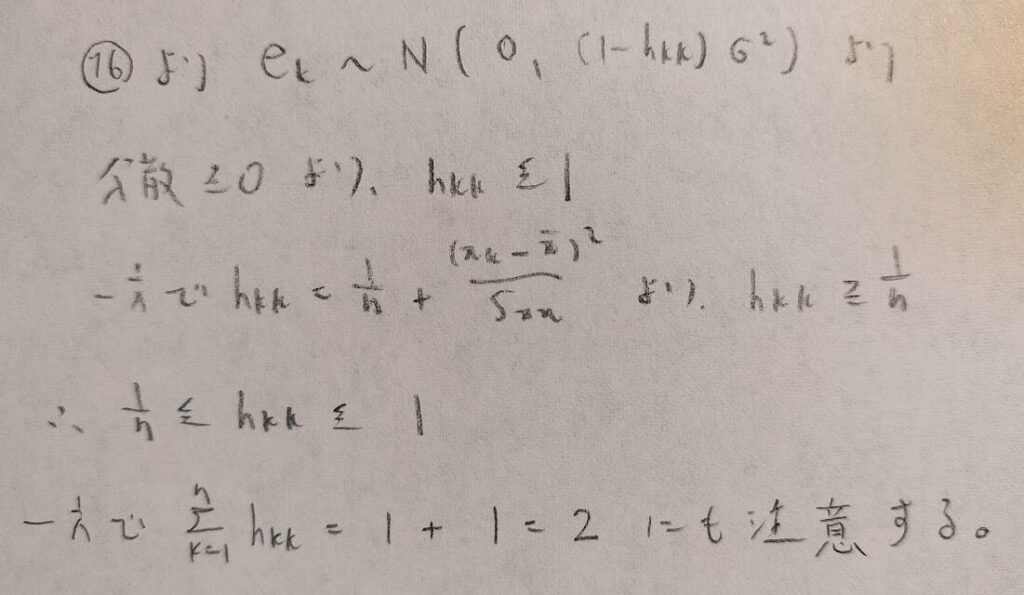
テコ比を検討するものとして、2.5に(テコ比の平均である)2/nをかけた値が目安として使われます。
なるほど!テコ比はxの値にのみ依存するので、データを取るときに可能ならば、テコ比が大きくならないようなデータを選んでおくということですね。
単回帰分析での残差分析の方法(t値登場)
これまでは回帰変動についての内容でしたが、残差変動についても、しっかりとした解析手法があります。
重回帰分析になると残差を1つ1つ調べるのは大変なので、残差を標準化して考える方法を学ぶ必要があります。
記事前半に登場した行列での計算における最後の式16をご覧ください。残差が従う正規分布を標準化したいのですが、母分散は未知ですので、推定値を用いるため、スチューデント化した量を残差のt値といいます。
対してもっと簡易的に、誤差項に注目した状態で、そのまま推定値を代入したものを、標準化残差といい、これらを用いて残差分析を行います。
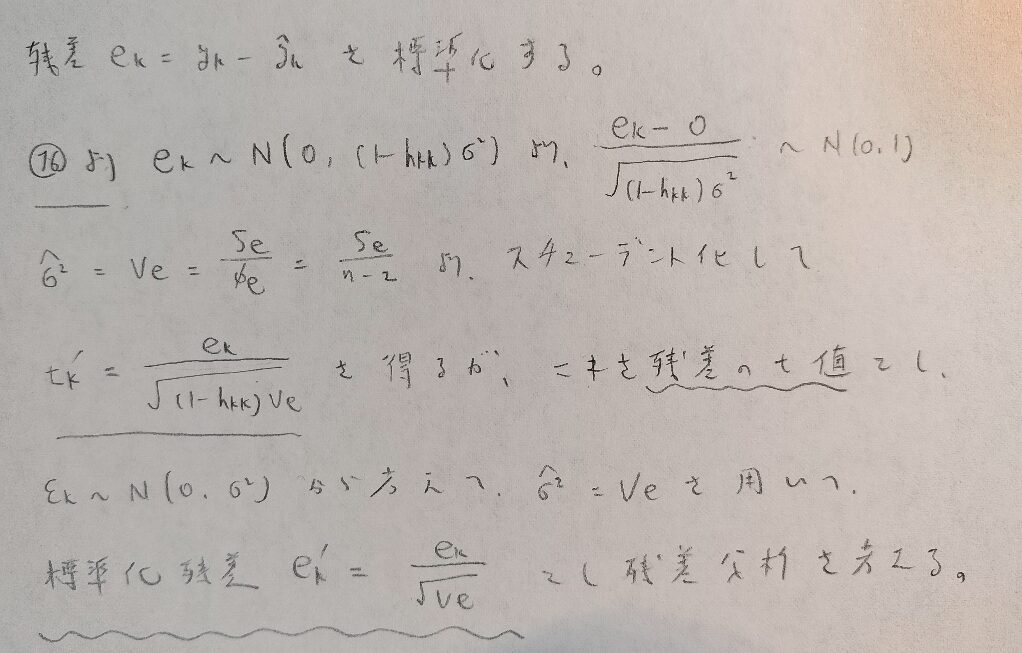
残差分析とはどのように行うのですか?
標準化残差ベクトルのノルムが3.0以上なら注意。2.5以上なら留意とします。また、xを横軸にとって、xに対応する残差(1変数)を縦軸にプロットしていきます。この残差プロットが原点を中心にランダムに分布していれば回帰分析は妥当と判断します。
単回帰分析に意味があるかの検定(t値とp値に注意)
以下では、有意水準εとして推定や検定を考えます。
そもそも回帰分析を行う意味があるのか?を調べるためには、今まで学んできた内容で理屈を構築することが可能です。
ここでも記事前半の行列計算で学んだ式10をご覧ください。その結果と、誤差項の母分散の推定値を用いることでt分布を導くことができます。そして自動的に誤差分散の推定量に自由度をかけたものを、母分散で割った量(つまり残差平方和を母分散で割った量)が自由度n-2のカイ2乗分布に従うことが導かれます。これは図11にて説明します。
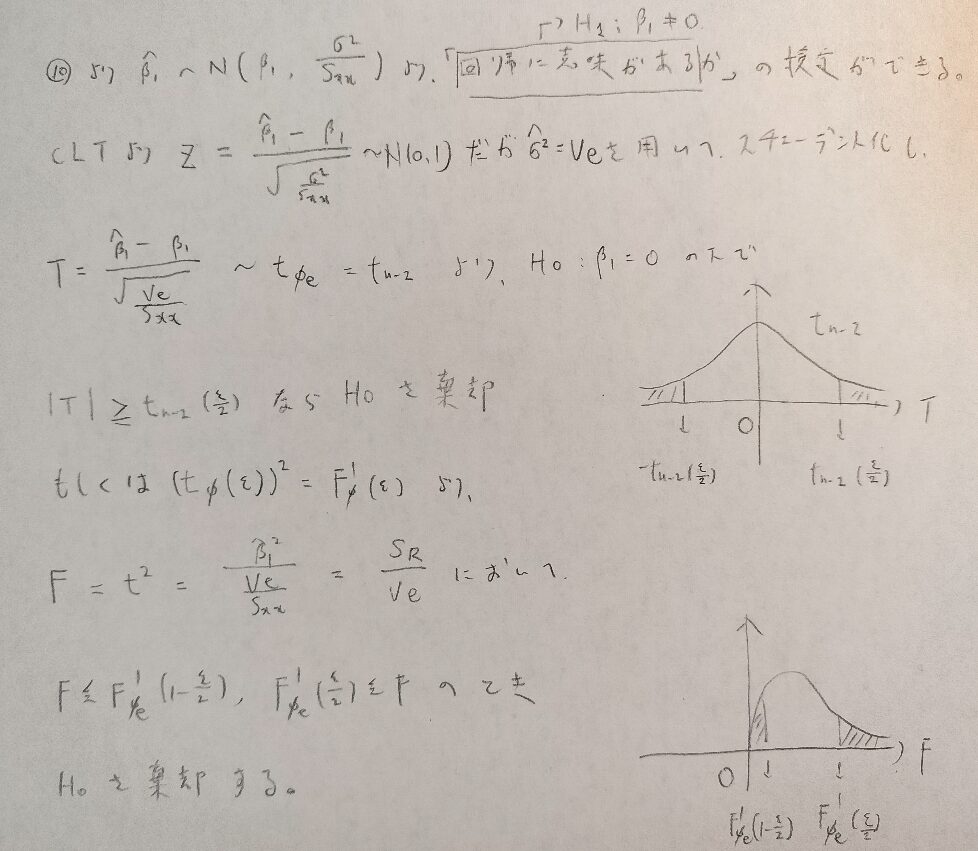
t値とは図10の斜線の位置のことで、p値とは実際に求めた確率を意味します。今回はp値が有意水準ε以下ならば帰無仮説を棄却します。
図09の最後の式では、残差変動が自由度n-2であることは暗に用いています。
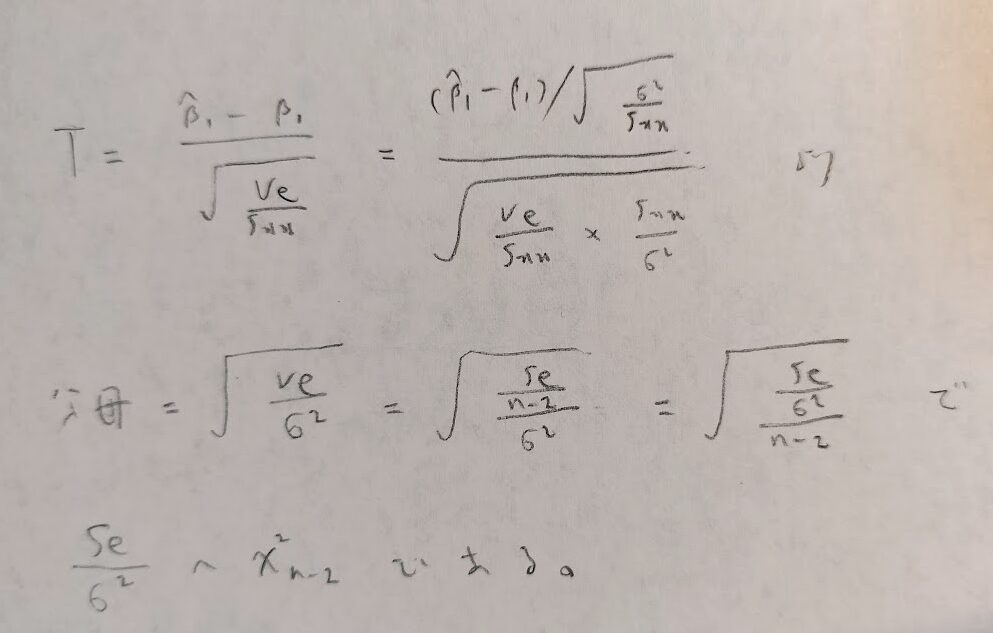
単回帰分析の予測区間の出し方を未来を例にしてわかりやすく説明
単回帰分析を用いて未来を予想したいのですが、どういった手順で予測区間を推定できますか?
ここまでで準備は整っていますので、1から順に説明していきましょう。最後ですので、一緒に頑張りましょう!
区間予測と区間推定は違います。まずは母回帰の区間推定を行います。次に予測区間を出します。予測区間はyの予測区間のため、誤差項εも含まれているため、分散が大きくなります。
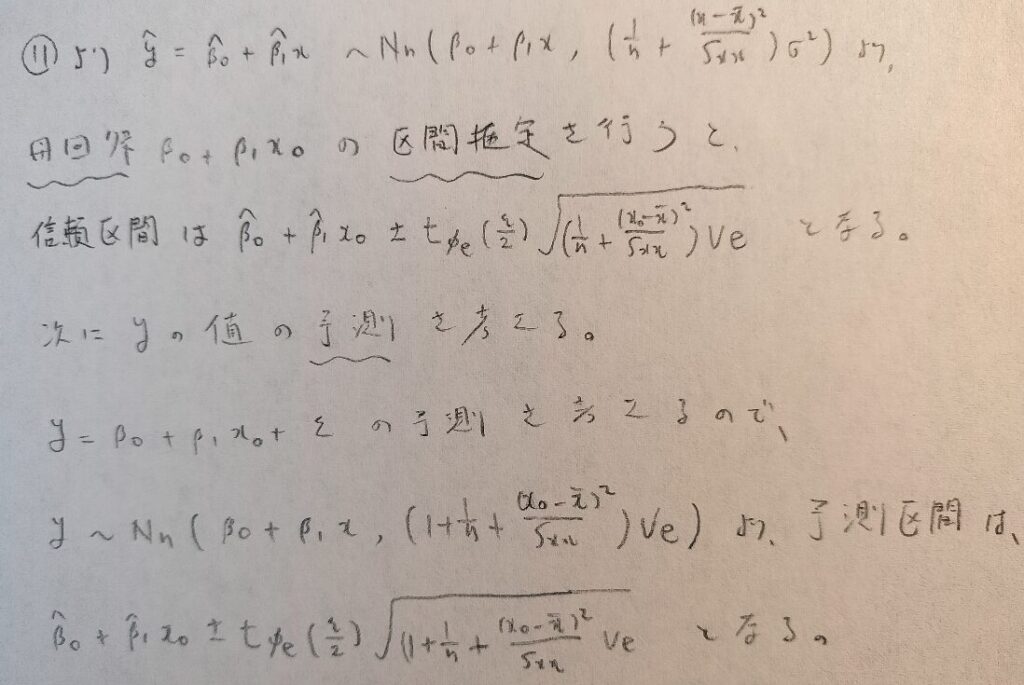
長かったです。でも私もこれで未来を予測する術を身につけることができました。
未来は直線的な関係だけでは表せないとは思いますが、少し先の未来ならば可能かも知れませんね。