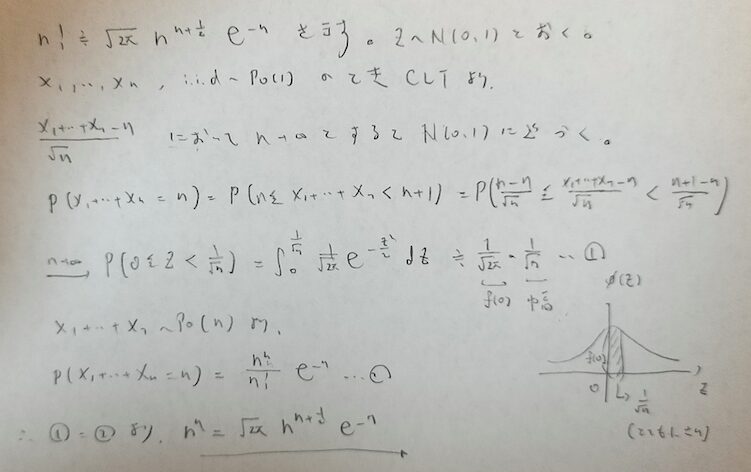統計検定1級で登場する頻出度が高くて最も難しい分布は多変量正規分布です。
多変量正規分布は主成分分析などの多変量解析にもつながる重要な分布ですが、とても難しくて挫折してしまいました。どのような順で勉強しなおしたら良いか教えてください。
多変量正規分布はアクチュアリー数学でも統計検定1級では頻出です。しかし参考書によって扱われている範囲が異なり、勉強していなかった部分が出てしまったとなりかねない分布です。
この記事は『増訂版 日本統計学会公式認定 統計検定1級対応 統計学』をベースに『現代数理統計学の基礎 』などに掲載されている定理などを体系立ててまとめ直したものです。あくまでも一般のn変量の理解を優先し、その具体化として2変量や3変量を扱っていきたいと思います。
多変量正規分布関連では統計検定1級の参考書が最も深い部分まで扱っていますので、こちらをメインに掘り下げていきます。
多変量正規分布の確率密度関数
まずは多変量正規分布の確率密度関数を紹介します。μやΣの正体は次の章で判明します。まずは形式的に置いておきます。
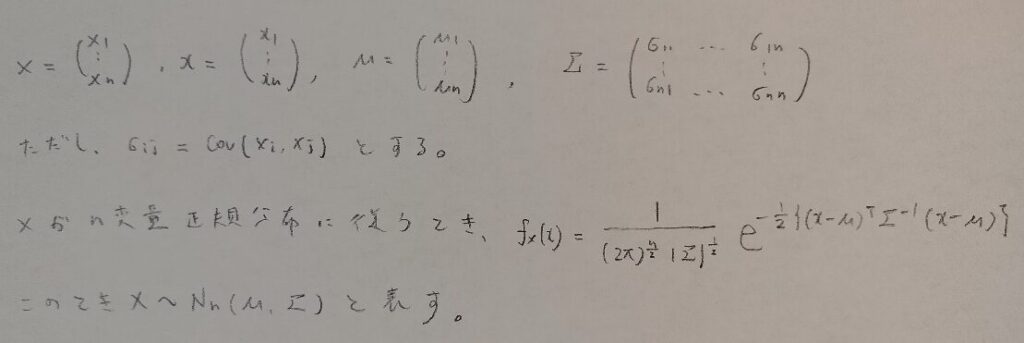
これをまず覚えられないのですが、どのような仕組みでこの確率密度関数が成り立っているのですか?
まずは自然対数eよりも左の正規化定数の部分を考えます。正規分布につく√2πがn個かけられていて指数部分がn/2になります。
なるほど。次のΣは一体なんですか?
このΣは分散の一般化で、分散共分散行列といいます。対角成分の第(i,i)成分はXiの分散を表しています。分散の記号と異なりますが、Σの形の覚えやすさを優先して行列表記に統一しています。非対角成分の第(i,j)成分はXiとXjとの共分散を表します。Σはその作られ方から対称行列です。
Σの逆行列を考えるので、厳密にはΣにはとある条件が課せられます。その条件は記事の後半で触れます。
なんとなく対応関係がわかってきました。Σの逆行列になっているのは、正規分布の確率密度関数の分散が分母にきているからですね。そして2乗に相当する部分が行列では転置で表現されているのも、いま納得しました。
多変量正規分布の積率母関数
図01において、期待値や分散は一体どこを見れば良いのか?と疑問に思いませんか?
多変量正規分布の確率密度関数の作られ方はわかりました。確かにそこから期待値や分散を求めるには、どこを見れば良いのか謎ですね。
それでは正規分布のときのように、積率母関数を計算して出してみましょう。積率母関数を出せればそこから期待値や分散が求まるからです。
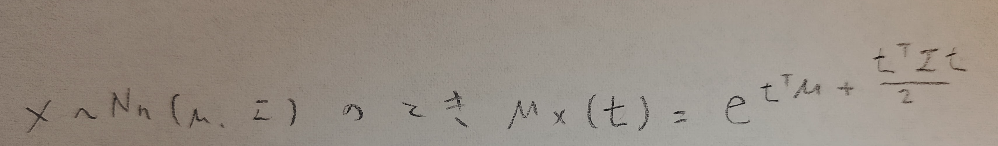
この結果も正規分布の積率母関数を一般化した表記になっているので、予想できたかと思います。その結果を証明してみましょう。
積率母関数の計算を積でどんどん繋げていきたいので、互いに独立な標準正規分布を設定する必要があります。確率変数Zに注目してください。
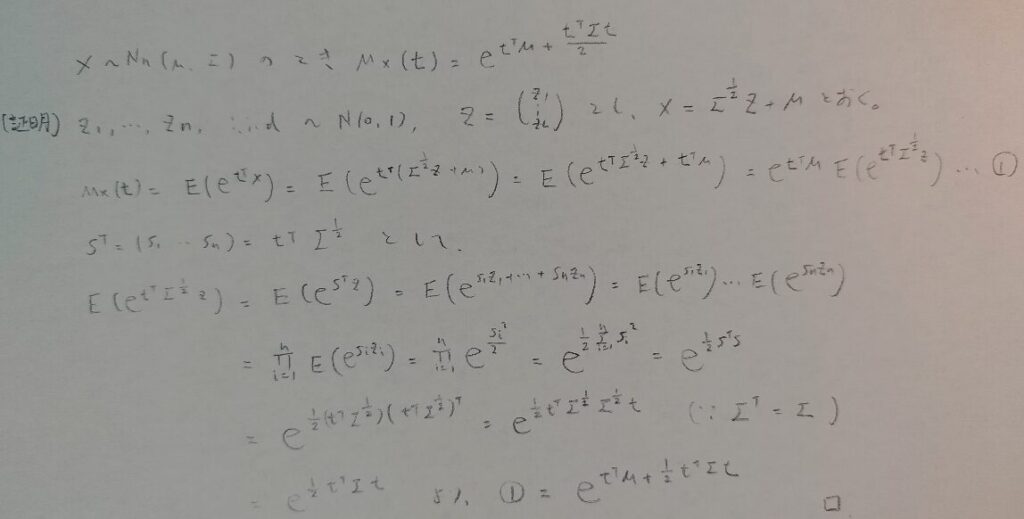
ではこの結果をテイラー展開して、多変量正規分布の期待値と分散に相当する量を確認しましょう。多変量正規分布の期待値に相当する量は期待値ベクトルμ、分散に相当する量は分散共分散行列Σで与えられることが確認できます。
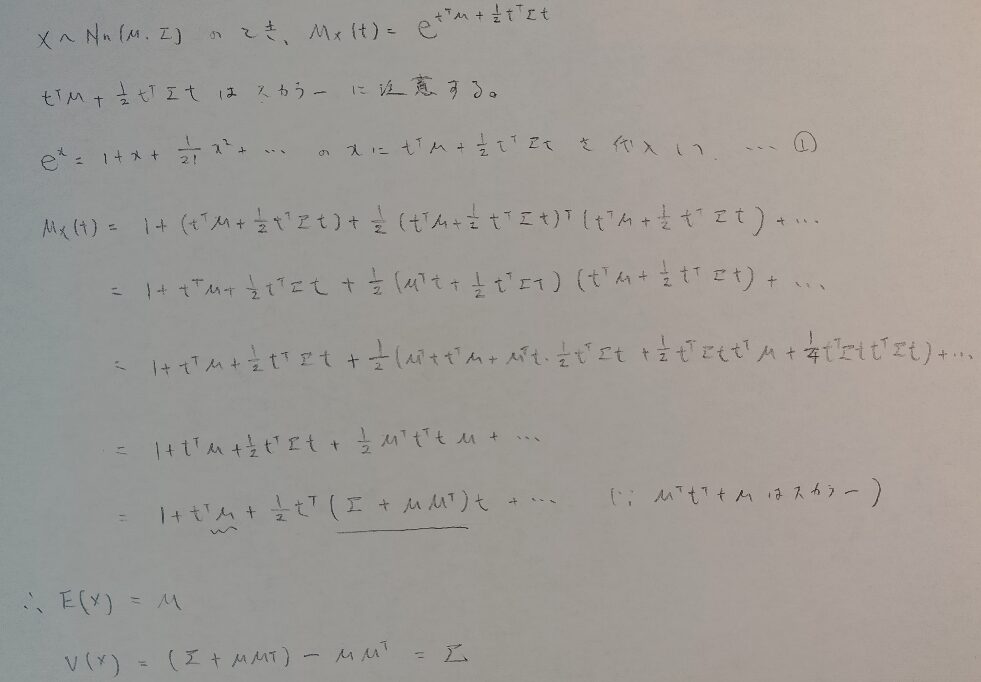
それでは、記事の後半で必要になる変数変換についても調べておきましょう。
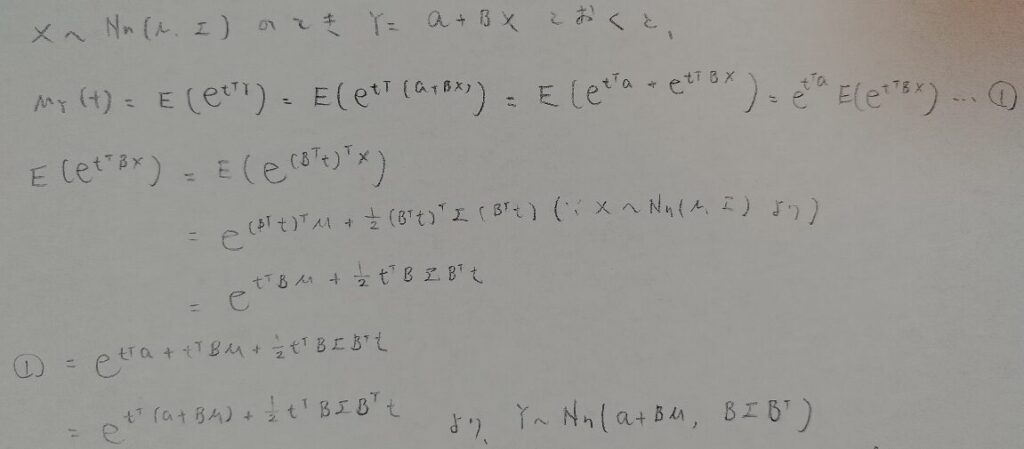
この結果も正規分布のときとまったく同じですね。表現が行列表示になっただけですね!
正規分布のときと同様に、多変量正規分布でも期待値ベクトルを0とし、分散共分散行列Σを単位ベクトルとすると、多変量標準正規分布ができます。

多変量正規分布のブロック表示
この記事のメインの部分です。『増訂版 日本統計学会公式認定 統計検定1級対応 統計学』にのみ掲載されている内容を、噛み砕いて説明します。本書の説明は行間が少ないので、この記事にて内容消化ができれば嬉しい限りです。
多くの参考書では、この次の話題で2変量正規分布に限定した議論になりますが、この記事ではn変量を貫きます。なぜなら統計検定1級や準1級では3変量まで出題されており、ゴリ押し計算では時間内に終わらないような計算量になるからです。そのため一般化した内容を消化することが大事だと判断しました。
多変量正規分布の各要素をブロック化します。その目的は条件つき確率分布をダイレクトに考えることができるからです。
まずは多変量正規分布の周辺分布も次元が下がった多変量正規分布となることを証明します。
まずはブロック化の様子をご覧ください。証明は図05を各ブロックに用いるだけという感覚的な理解で済みます。これがブロック化の強みです。
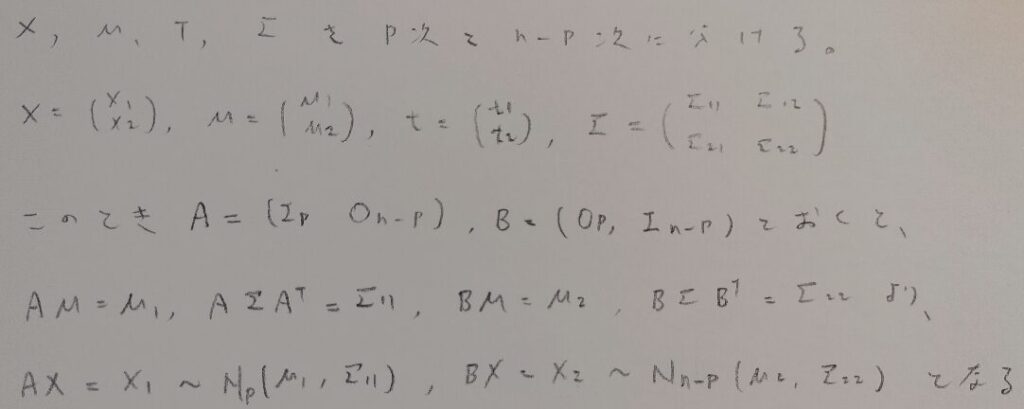
多変量正規分布の条件付き確率分布
本記事で最も難易度が高い部分です。この最終結果がとても大切なので覚えてしまいましょう。証明はとてもテクニカルです。
片方がわかれば、もう片方は対称性より自動的に分布の形が判明します。まずは片方の部分だけ求めてみましょう。
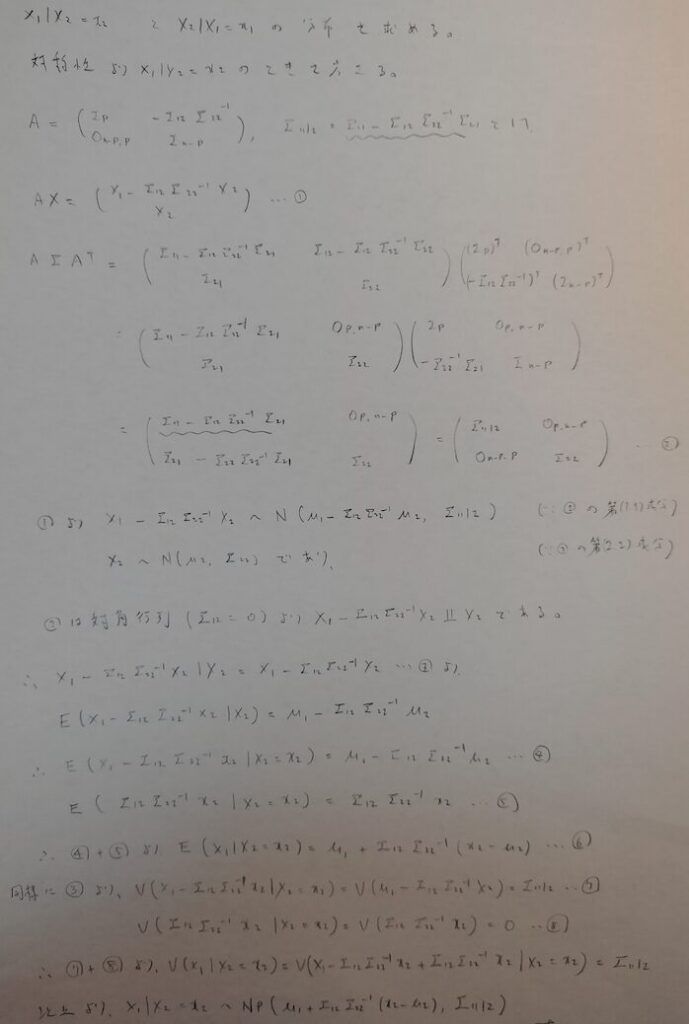
もう片方の方もお願いします!
図08の流れを汲むと、次のような結論になる予想を立てるのは難しくないと思います。
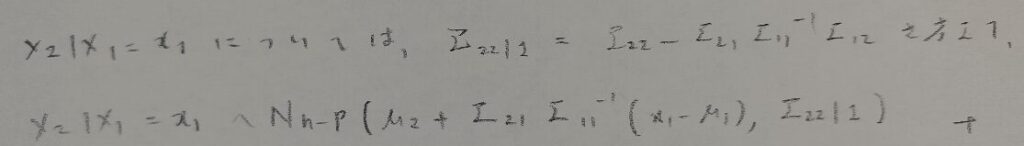
正規分布における独立性と無相関の同値性
一般に独立ならば無相関は成立します。しかしその逆は成り立ちません。しかし正規分布を考えると、独立性と無相関は同値関係になります。
この証明は有名ですので、一緒に考えていきましょう。すなわち無相関ならば独立を証明します。無相関とは共分散が全て0ということです。
証明の流れは積率母関数の関係性に帰着させる方針で行います。
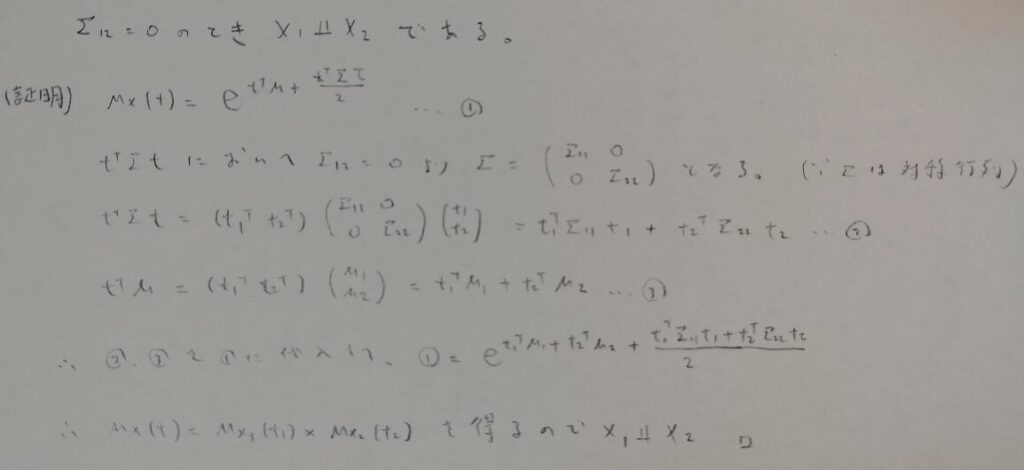
この証明はとても鮮やかです!分散共分散行列の非対角成分が0だということを仮定に用いているのですね。しかもΣは対称行列だから、仮定するのは非対角成分の半分の部分でOKなんですね!
2変量正規分布の頻出問題
統計検定1級やアクチュアリー数学で頻出なのが2変量の正規分布です。どのような聞かれ方をしても対処できるように、よくあるパターンを体系立ててまとめておきます。
まずは最もよく目にする2変量正規分布の確率密度関数を導いておきます。n変量の公式を具体化して計算していくだけですが、計算量が多いです。
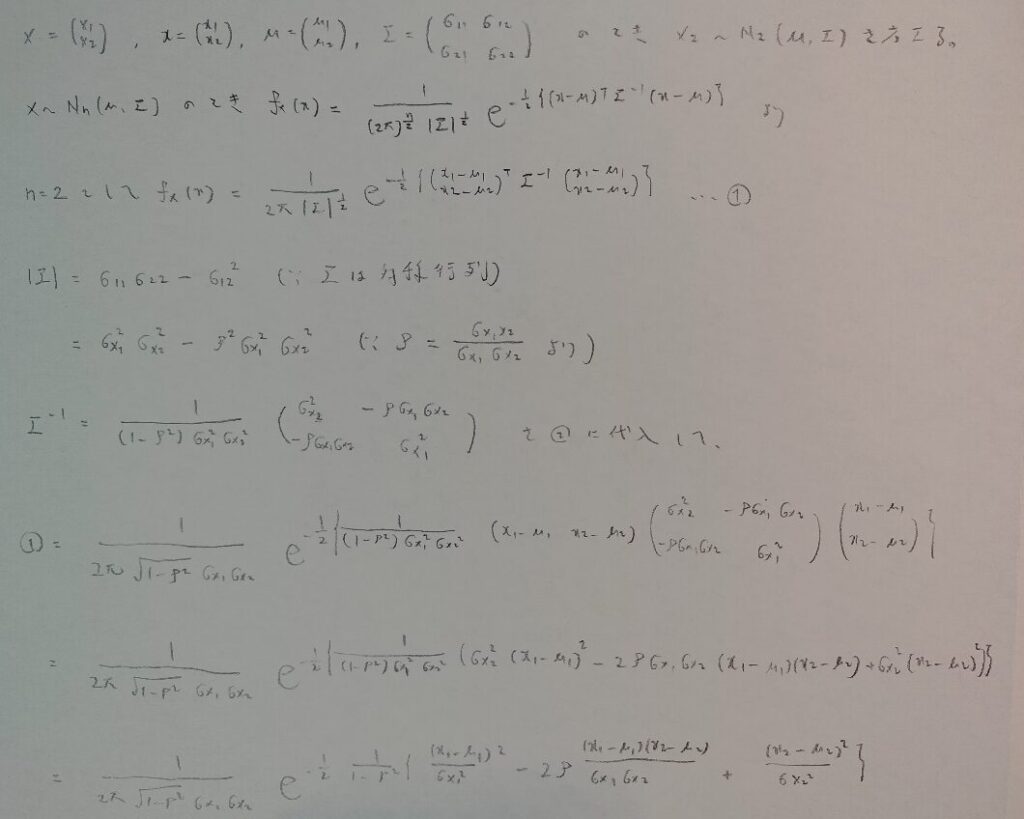
アクチュアリーでほぼ公式として出てくる2変量正規分布の条件付き分布関連もお願いします!
『アクチュアリー試験 合格へのストラテジー 数学』に公式として載っているものの証明を行います。この本は圧倒的な公式が載っており、アクチュアリー数学の受験をしない方でも、有名な確率分布やモデリングなどの知識を体系立てて得られる名著です。
平方完成がとてつもないくらいの難しさです。これを試験会場で行うのは不可能に近いです。公式を覚えてしまいましょう。のちに記事にする回帰直線の話題につながります。

高校1年生で勉強した平方完成が本気を出したらこんな問題になってしまうのですね。
最後は2変量正規分布と独立性と無相関の同値についての証明です。図12からの流れで証明できるのが、とても美しいと思いませんか?
証明は☆の式だけを用います。図13の証明のような確率密度関数の変化に注目してください。
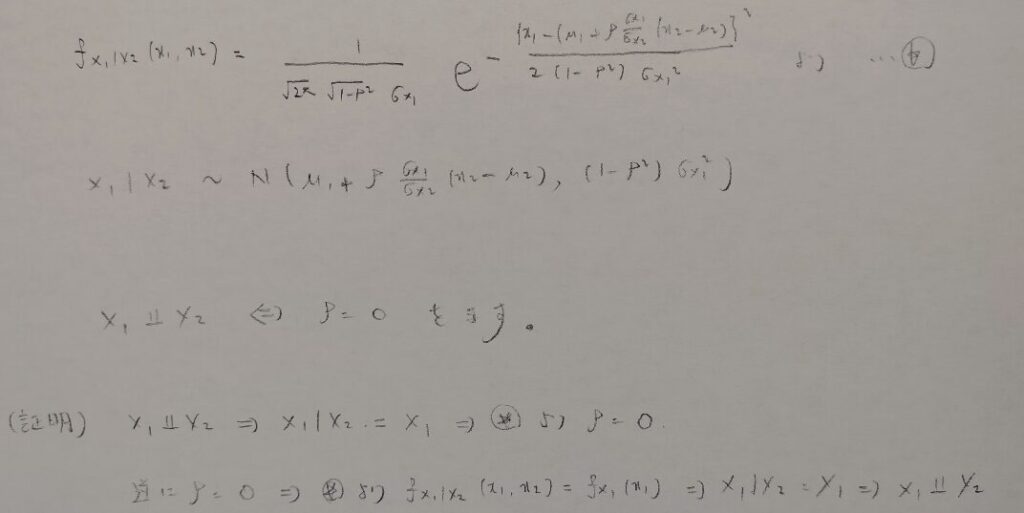
3変量正規分布の頻出問題(統計検定準1級の過去問)
2変量でも計算地獄なのに、3変量だと半日かかってもおかしくない計算量になりません?笑
冗談ではなく、本当にそれくらいかかる計算になりそうな問題を紹介します。統計検定準1級の過去問から表現を変えて出題します。
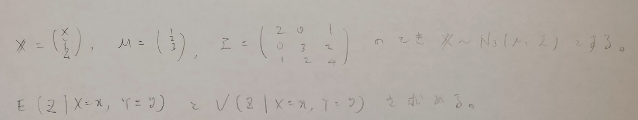
3変量以上になると手計算は非現実的です。そのためn変量のときに勉強した公式(図08)を用いましょう!
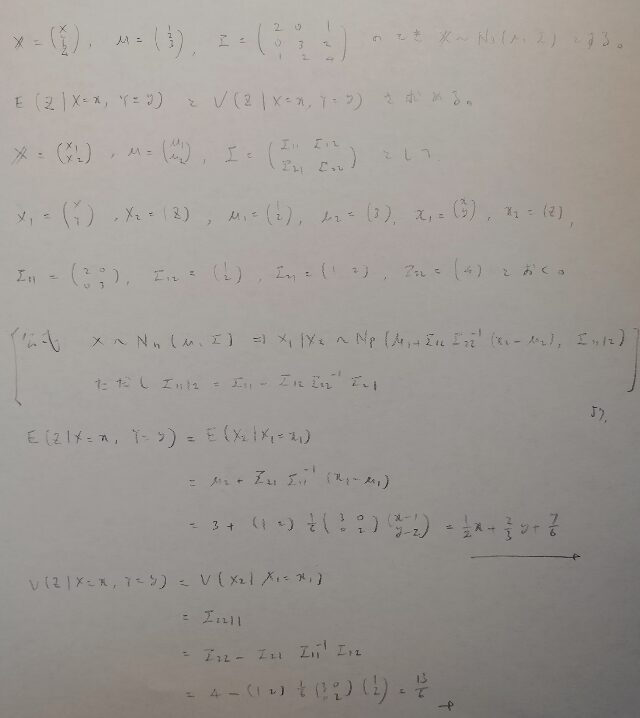
分散共分散行列は半正定値
多変量正規分布に限らず、分散共分散行列は重回帰分析や分散分析、そして主成分分析などでとても大事な役割を演じます。その分散共分散行列Σの大事な定理を紹介します。
分散共分散行列は半正定値です。
なるほど。分散共分散行列の一般としての性質を紹介したくて、最後に持ってきたのですね笑
半正定値は2次形式の値が0以上になることをいいます。ただし定義域(下の証明ではベクトルyのこと)は0ではないとします。そして半正定値とはΣのすべての固有値が0以上と同値です。
それではΣが半正定値であることを証明します。
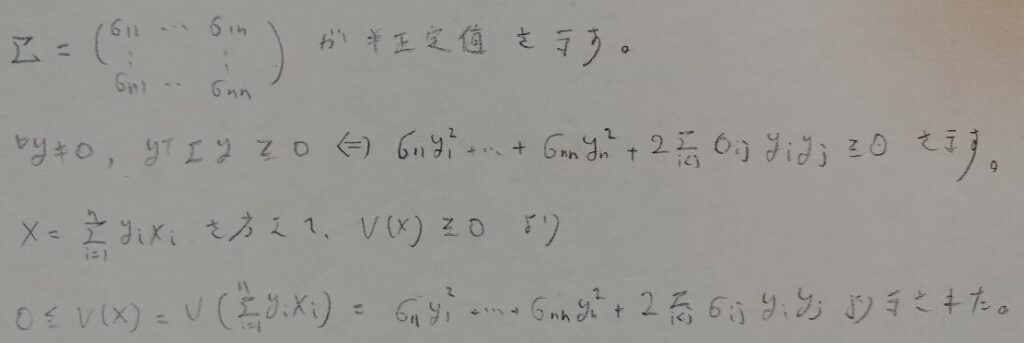
多変量正規分布の確率密度関数の式を思い出してください。特に記事冒頭の図01をご覧ください。ここにはΣの逆行列がありますよね。もしもΣが半正定値だと固有値が0になるものがないとは言い切れないので、逆行列が0になる可能性が出てきます。このことはΣに逆行列が存在しないことを意味します。そのため多変量正規分布ではΣは正定値という仮定が前提として必要になります。
多変量正規分布においてΣは正定値とする。この仮定をもとに、もう一度この記事を読み返してみてください。きっと理解が深まります。
今回はブロック化がとても便利だと気付かされました。ありがとうございました!