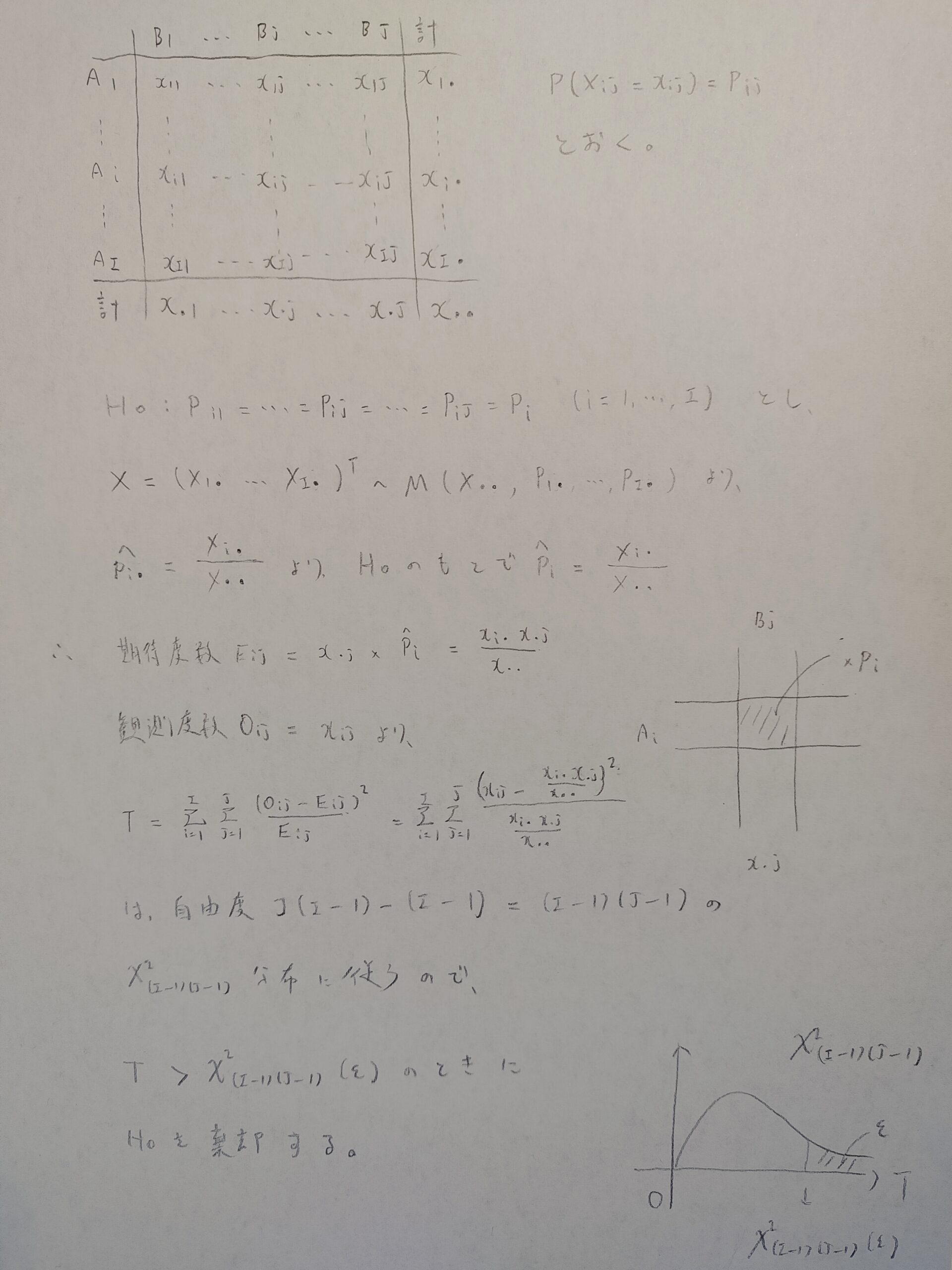前回で勉強したカイ2乗検定(適合度の検定)を基本として、クロス表(分割表)を利用するさまざまなカイ2乗検定を紹介します。理解としてつながる順番(同等性検定・独立性の検定・正確性の検定・マクネマー検定)で解説していきます。
適合度の検定で、学んだピアソンのカイ2乗検定統計量がカイ2乗分布に従うことを次の記事でご確認ください。
今回勉強する、同等性検定・独立性の検定・正確性の検定・マクネマー検定などではカイ2乗分布の自由度に関する考察が大事になります。その都度、自由度はいくつになるのか?を一緒に考えていきましょう。
その他にも意識する点を3つに集約しました。ご確認ください。
カイ2乗検定の考え方として、次の3つを意識してください。
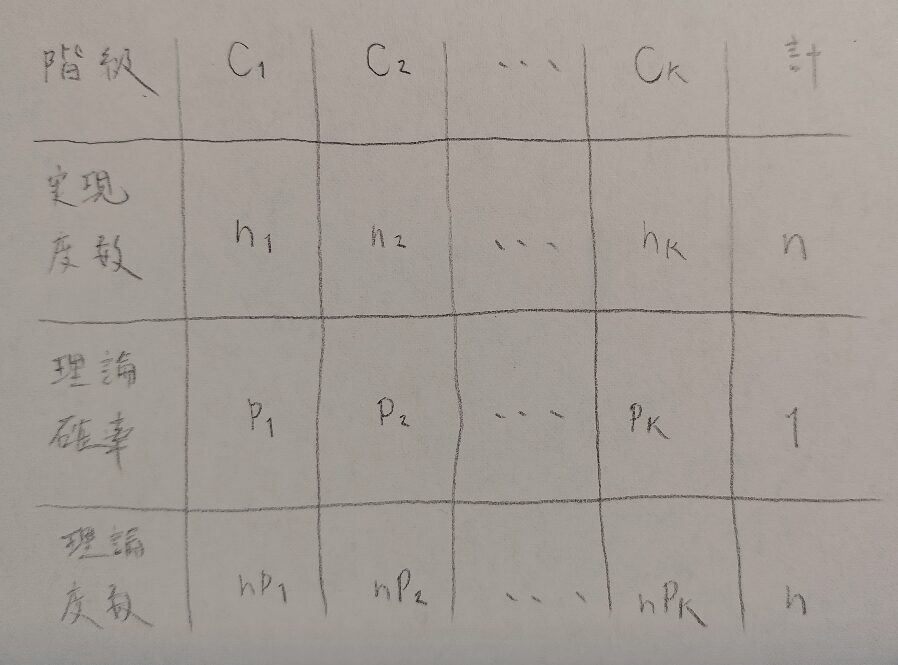
1.多項分布から開始し、確率の推定量を求めてから期待度数を考える。
2.帰無仮説はどのように設定されているか?を理解する。
3.カイ2乗分布の自由度を出す際の根拠を意識する。
この記事では有意水準をすべてεに統一します。
同等性検定
適合度の検定からすぐにできる応用として、同等性検定を学びます。
『データ解析のための数理統計入門』では同等性検定の例として小説家の例があげられています。
たとえば同じ人物がいくつかの小説(下記の図01の表のBの要素)を書いて、その中に登場するいくつかの単語の数を調べたデータがあるとします。そのデータを調べて(同等性の検定)、単語数(下記の図01の表のAの要素)の偏りの多さ、少なさから、その小説が同一人物による創作なのかを考えるときに用いることができます。
同等性検定は、いろいろな場面で活躍してくれそうな検定ですね!
それでは同等性検定の流れを説明します。帰無仮説と、多項分布の利用に注目してください。多項分布は期待度数(理論度数)を計算する際の確率を求めるときに用います。カイ2乗検定が絡む場面の序盤では多項分布を考えていくことが多いです。
対立仮説は「J冊の小説に登場するi番目の単語が登場する確率が全て等しくはならないような単語が少なくとも1つ存在する」つまり同一著者とは言えない、という意味です。
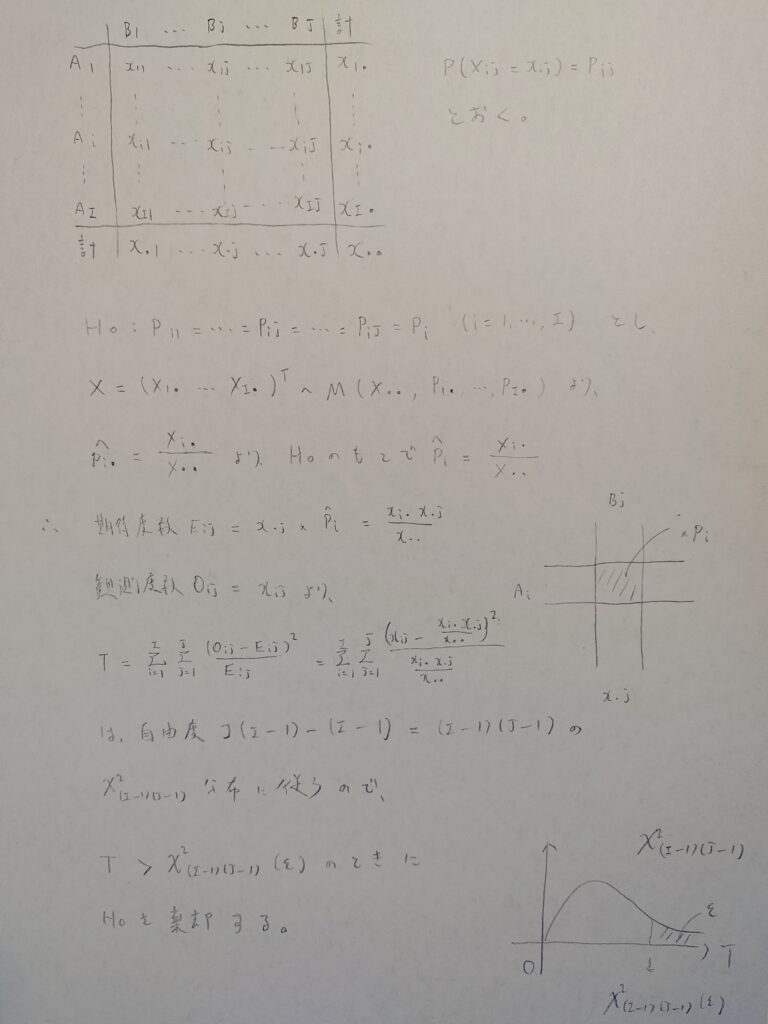
自由度について、なぜこの結果になるのかが分からないので教えてください。
まずは自由度は確率から考えていけば分かりやすいです。確率和が1であることに注意してください。帰無仮説が与えられたときの自由度はいくつになりますか?
さきほどの例では小説の数をJ冊で単語の種類をI種類と考えてみます。帰無仮説では、どの小説に登場する単語が出てくる確率も等しいとしているので、小説の種類は関係ないですよね。そして全確率が1なので、自由度はI-1になります。
その通りです!全体の自由度では、帰無仮説を与えたときの自由度I-1に、小説の冊数Jを掛けたものになります。
なるほど!だからカイ2乗分布の自由度はそれらの差で求まるということですね。
独立性の検定
I ×J表
次に、帰無仮説を少し変えたバージョンである独立性の検定を学びます。こちらはアクチュアリー数学で頻出のカイ2乗検定となります。
独立性の検定を行う流れを紹介します。
対立仮説は「AとBは独立とは言えない」です。

帰無仮説の数式について解説をお願いします。
これは高校数学で学ぶ考えと基本的には同じです。
例えば2つの確率変数XとYが独立のとき、「Xがxという実現値をとり、かつYがyという実現値をとる確率」は「Xがxという実現値をとる確率(Xの周辺分布を考えている)」と「Yがyという実現値をとる確率(Yの周辺分布を考えている)」の積に等しくなります。この周辺分布を考えたときの数式が帰無仮説の数式を意味しています。
自由度については、全体の自由度は表の中のセルの数であるIJ個の確率を全て足したら1なので、自由度はIJ-1ですね。
帰無仮説を与えたときの自由度は、周辺分布の全体の数であるI+Jを考えます。しかし各周辺分布の確率和は1なので、自由度としては(I-1)と(J-1)の和になります。それらの結果からカイ2乗分布の自由度が得られます。
2×2表
アクチュアリー数学の独立性の検定では2×2表に限定したものが頻出です。
2×2表の場合の独立性の検定では時短可能な計算公式があります。試験ではこれを用いて解くことになります。
では、2×2表の公式を導出してみましょう。計算量が尋常になく多いだけで、やっていることは複雑ではありません。
この式の導出は有名参考書にはないので、しっかりと学習したいですね!

この公式は実は使用に制限があります。イメージ的にはnが小さいと使用できないということです。詳しくは次のイェーツの補正の章をご参照ください。
要するにnが大きくないと正確性の部分で良くないということですね。数式での説明をお願いします。
まず前提として、nが小さいとTの値が大きく出過ぎてしまうので、なんとかしてTの値を小さくするための工夫が必要になります。具体的にはイェーツの補正で解説します。
イェーツの補正
nが小さいときは次のイェーツの補正を行います。具体的には4つのセル(a,b,c,d)に対応する期待度数のうち少なくとも1つが5以下のときにイェーツの補正を検討します。
合計値を一定にしたまま、Tの値を小さくする工夫を考えることになります。
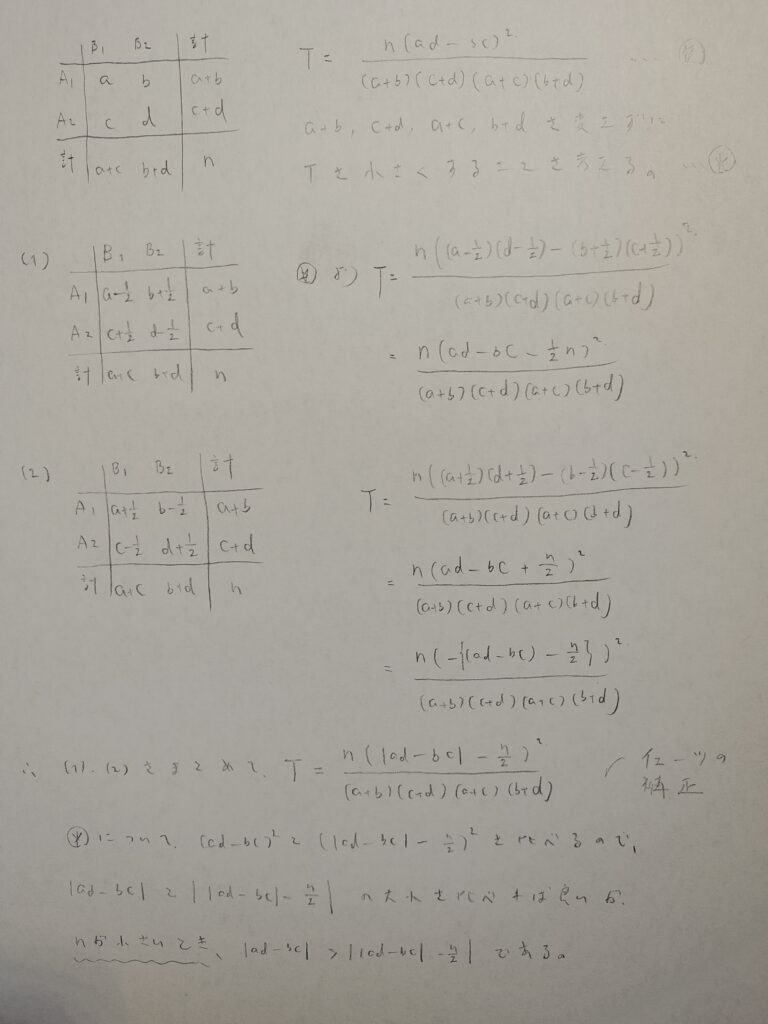
先ほどの質問の考察を※に書きました。つまりnがある程度小さいときはイェーツの補正が有効ということです。
しかし、イェーツの補正を行う前に、より正確な検定が可能なフィッシャーの正確性検定を検討した方が良いとされています。
フィッシャーの正確性検定
フィッシャーの正確性検定でも、イェーツの補正の考えと同じように、周辺部分を固定して考えます。
フィッシャーの正確性検定では、4マスの値(この2×2表では4変数の同時分布)を実現する確率を直截出していくことになります。
図05では2×2表のよくあるパターンを解説し、最後にI×J表の場合に一般化します。フィッシャーの正確性検定は、nが小さいときだけではなく大きい場合でも使用できるからです。
この確率の出し方は2通りあります。1つは図05のような思いつきやすい方法です。もう1つは後述する超幾何分布を利用する方法です。

超幾何分布を用いた出し方を教えてください!
了解です。まずは超幾何分布について復習します。
N個の中に当たりがM個あります。そこからn個を取り出します。n個の中にはX個の当たりがあります。Xを確率変数とするときに、Xは超幾何分布に従います。このことをX~H(N,M,n)と表現します。(H記号は例えば『リスクを知るための確率・統計入門』で使われています。)
https://www.muscle-castle.com/hypergeometric-distribution-expected-value-variance/
まずは超幾何分布を用いた計算式は次のようになります。
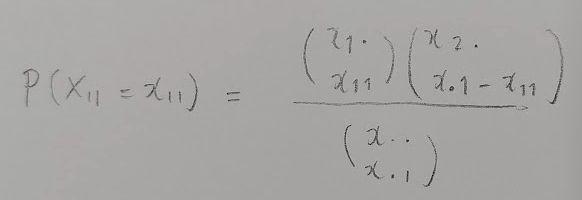
ただし超幾何分布は次のように設定しています。

図06の式が作れる意味を解説してください!

フィッシャーの正確性検定は、複数の2×2表を用いて得られた確率を足したものをP値とし、P値の値と自由度1のカイ2乗分布の上側ε点との比較を行うことにより、帰無仮説を棄却するかを判定する検定なのですね。
カイ2乗検定のうち、もう1つ面白い検定がありますので、最後にマクネマー検定を紹介します。
マクネマー検定
最後にマクネマー検定を解説します。マクネマー検定では表の中の設定が少し特殊ですので、まずはこちらを解説します。
まずは図09をご覧ください
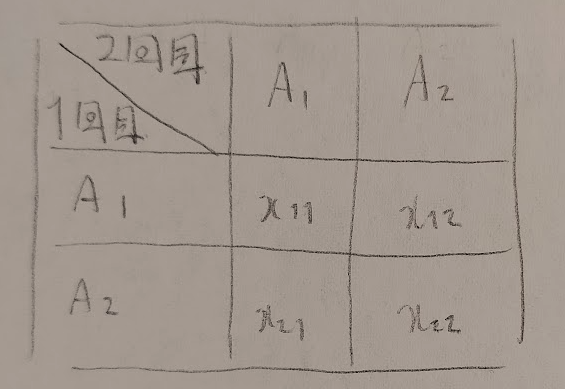
あれ?表頭(縦)も表側(横)も同じAで考えていますね。違うのは1回目と2回目。これは一体どのような検定なのでしょうか。
マクネマー検定は同じ試行(結果は2通り)を2回繰り返したときに、1回目と2回目で結果に差異があるか?を調べるための検定です。
マクネマー検定も2×2の独立性の検定のときと同じくイェーツの補正があります。使用条件は記事の最後に紹介します。
なるほど。納得しました。
では実際にマクネマー検定の流れを導いてみます。図09と合わせてご覧ください。
ポイントは帰無仮説により、「何を無視してよいか」と「事象が2通りあるので、二項分布を用いる流れ」に気づくかどうかです。また、帰無仮説を仮定しているので振り分けられる確率は1/2とすることも大事です。
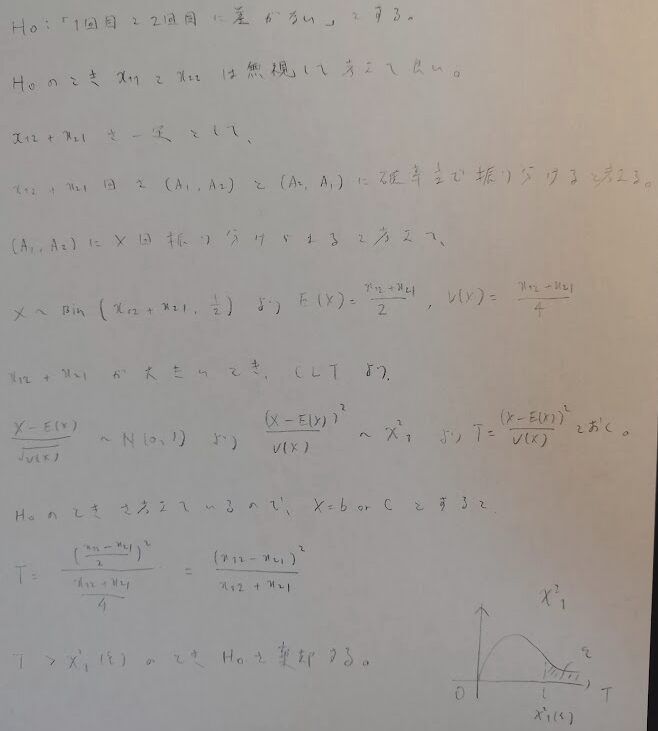
マクネマー検定は、二項分布→正規分布→カイ2乗分布の流れになっていて綺麗ですね。
その通りです。確率分布間の性質を知ることで、新たな検定が導かれたのは美しい流れですね。
マクネマー検定におけるイェーツの補正の使用条件は次の通りです。
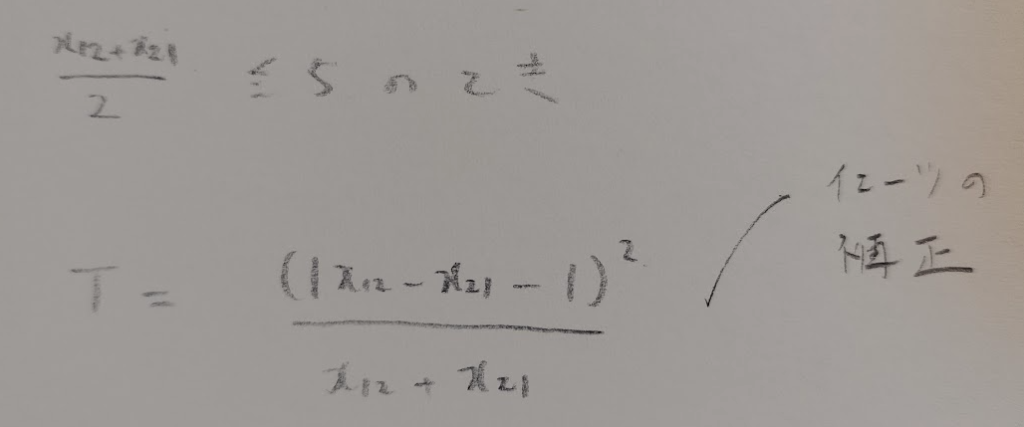
2×2の独立性の検定のときのイェーツの補正の式と似ているので覚えやすいですね!