統計検定1級の対策書として公式本以外で真っ先に買うべき本である『データ解析のための数理統計入門』の第13章の解説と演習問題を自力で解いた学習の軌跡の記事です。本章は回帰分析の応用になります。アクチュアリー数学では超頻出ですが、統計検定1級ではあまり出にくいようです。しかし共通問題で出てきそうな予感がします。出てくれた場合は確実に誘導に従って完答したい分野です。
ロジスティック回帰→プロビットモデル→ポアソン回帰の順で学習します。主にロジスティック回帰の内容に重きを置いています。
本記事のみでは物足りない場合、対数線形モデルへの応用などの別記事も紹介しています。併せてご覧ください。
統計検定1級青本の第13章の説明と例題
本記事はガウス・マルコフの定理より先の内容が難易度が高くなっています。ガウス・マルコフの箇所を前半としたのはアクチュアリー数学での重回帰分析の区切りの部分であるためです。要するに後半は統計検定1級に相

ロジスティック回帰モデルは、単回帰の出力がロジット変換後の値となっているということです。つまり線形回帰の出力が直接確率を表すわけでなく、事象が起きるオッズの対数を予測しているというわけです。
ロジスティック関数周辺の話題はAI関連の内容でも重要です。以前僕が受験して合格したG検定でも関連話題が出ています。またロジット変換の逆関数がシグモイド関数とも言います。ちなみに本書ではロジスティック関数と呼んでいます。
ロジスティックモデルの作られ方を分布関数の観点から考察します。これによりプロビットモデルも定義されます。

ロジスティック回帰において尤度でベルヌーイ分布を用いた箇所を二項分布にすることにより2値ロジスティック回帰も定義されます。これは回数nも問題文で与えられているときに用いられます。
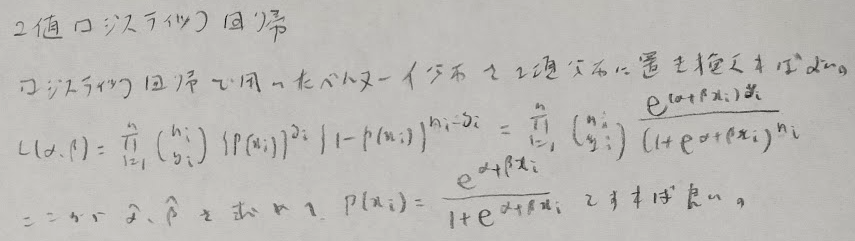
今度は複数の共変量(yを説明するxの成分が複数あるということ)を持つロジスティック回帰を考えます。これは通常のベルヌーイ分布を用いたモデルを行列表現に拡張したものです。
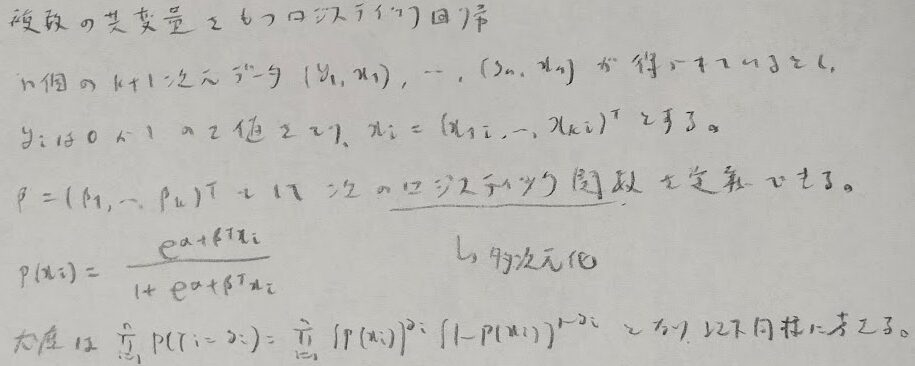
最後にポアソン回帰を扱います。これは稀にしか起こらない事象のデータがnという階層(例えばnは年齢の階級に相当する場合など)と共に用いられるモデルです。リンク関数がロジスティック回帰の場合と異なることに注意しましょう。
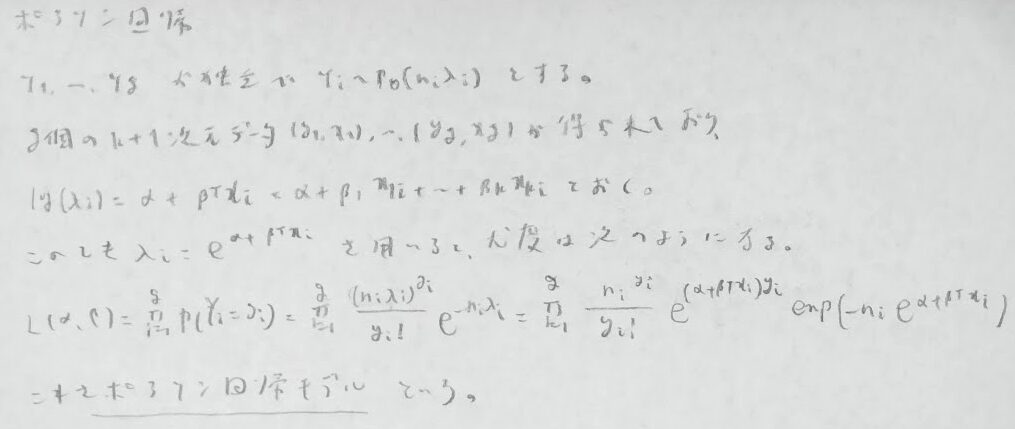
統計検定1級青本の第13章の演習問題
問1:シグモイド関数関連
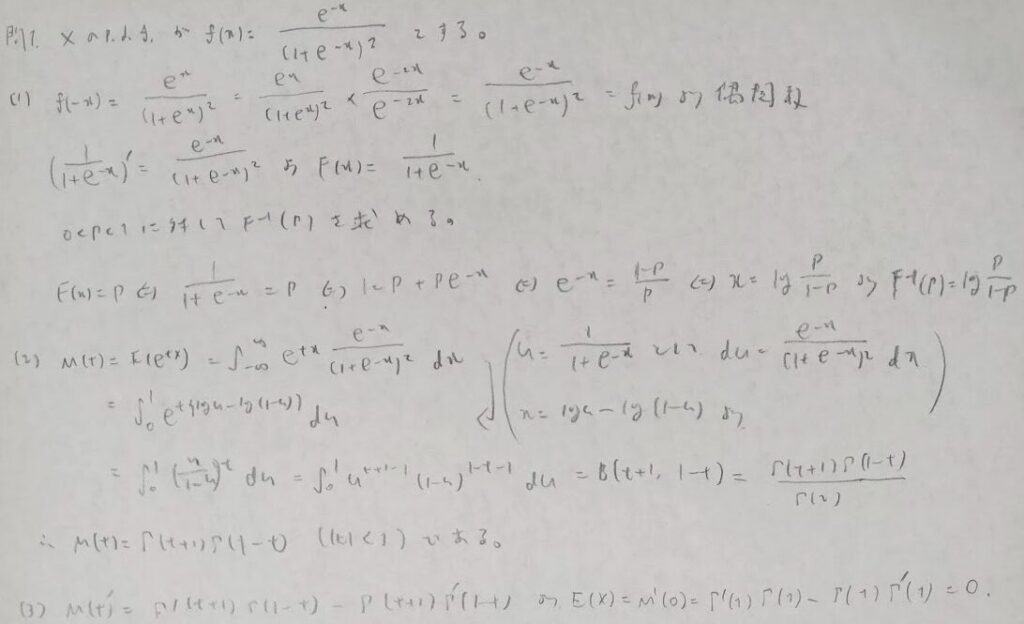
問2:プロビットモデル
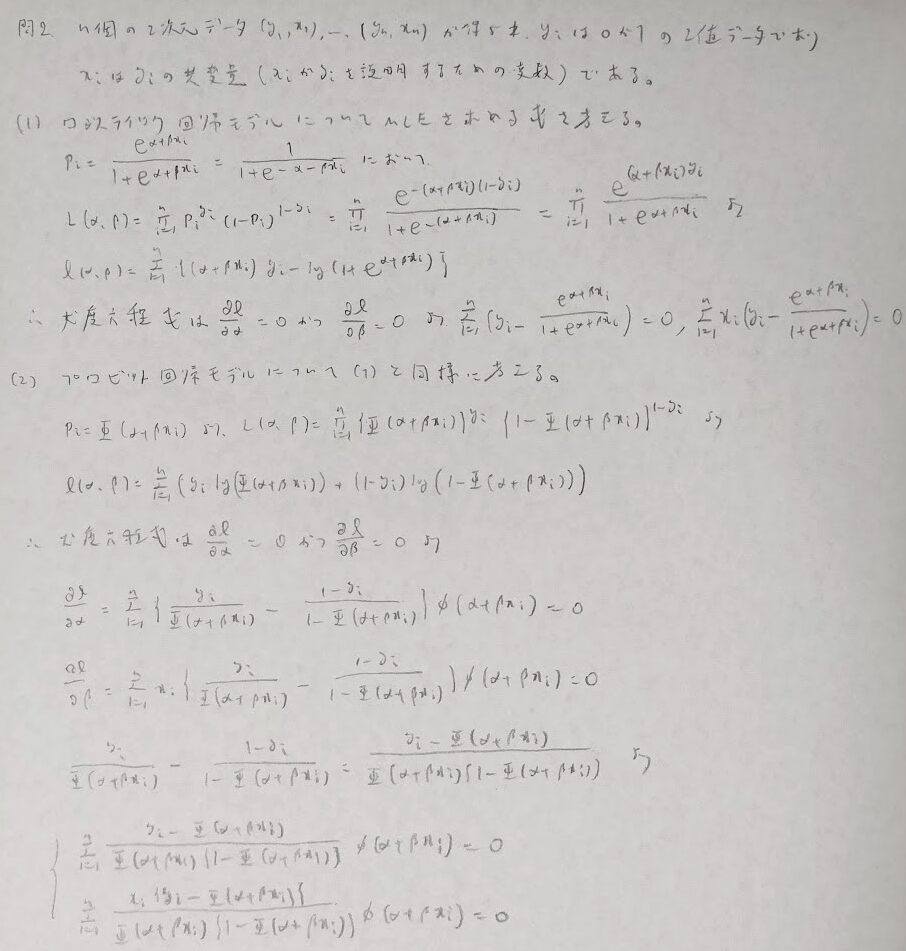
問3:ポアソン回帰

以上で回帰分析の応用は終了です。統計検定1級で出題されることは少な目ですが、もし出た場合は高得点が狙える分野ですのでお互い頑張りましょう!
異なる角度からこの分野を記述した記事が下記になります!よろしければ併せてご覧くださいね!