実験計画法について『データ解析のための数理統計入門』の内容を学習していきます。本書の方向性としてはQC検定2級で出題される1元配置と2元配置の分散分析表を作成する過程までの数理的側面に言及をしています。統計検定準1級以上やQC検定1級に出題されるハイレベルな実験計画法まではカバーしておりません。ただし1元配置モデルにおける多重比較の問題についてしっかりと触れており、類書にはない演習問題に触れることができます。
本記事では1元配置モデル→多重比較検定→2元配置モデルというシンプルな構成になります。ただし多くの学習者が避けがちな平方和の期待値など数学的に込み入った内容についてこちらで途中式などを詳しく解説しております。
データ解析のための数理統計入門の第15章『分散分析と多重比較』の例題と解説
フィッシャーの3原則は反復、無作為化、局所管理です。反復は推定誤差を小さくするために行います。無作為化は誤差は偶然誤差と系統誤差の2種類があり、系統誤差の緩和に貢献します。局所管理は均一条件下での実験が目的です。
実験において処置群と対照群があります。処置群は実際に処置を受ける側です。対照群は処置群と比較するために設定される基準となるグループです。
1元配置分散分析
各αを(主)効果といい、実験で取り上げた因子の各水準の効果を表します。μは一般平均と言われます。主効果を測定するためにある水準の状態での実験を複数回繰り返します。このときの(標本)誤差もモデルに設定します。この標本誤差は互いに独立で正規性を仮定します。
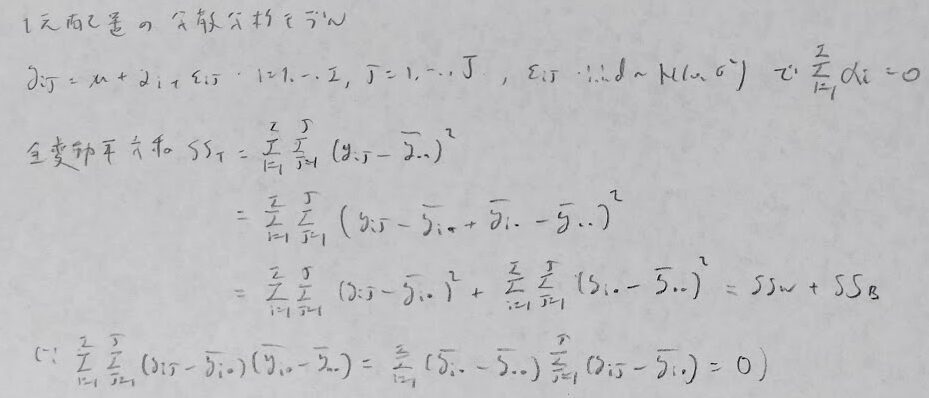
仮設検定について議論をするために必要な性質を順に導きます。ここの箇所は他書ではあまり触れられていませんが、『データ解析のための数理統計入門』ではここの理論的な部分がしっかり記述されているので理論的な背景の理解が助かりますよ。
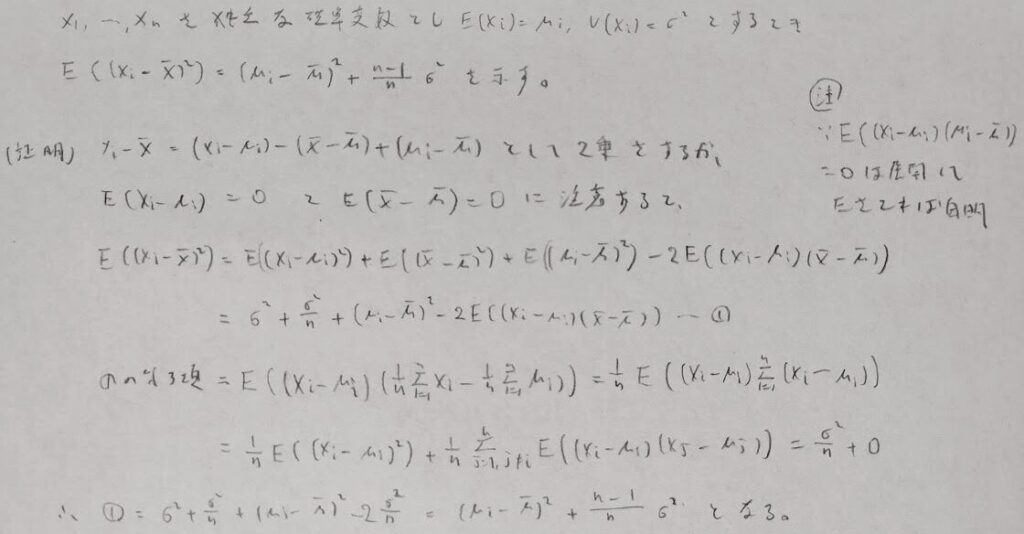
上の内容は実験計画法に関係なく成り立つ成立する内容です。この関係式を本章の内容に適用させたものが次になります。つまり群内平方和と群間平方和の期待値を導出します。
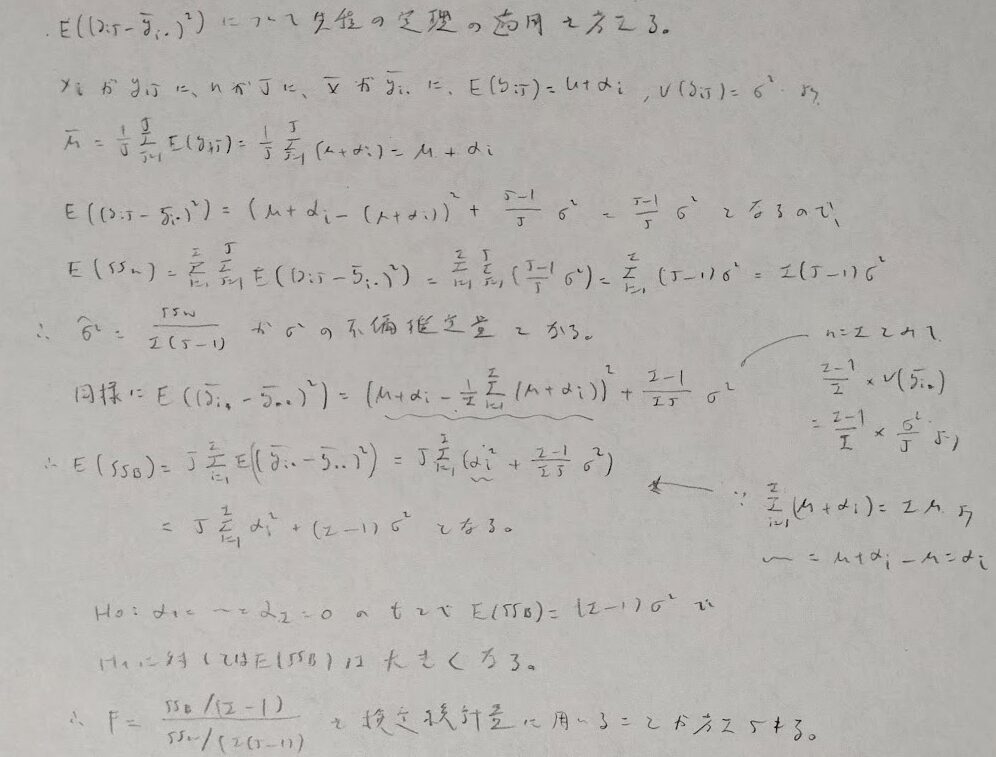
それではこのFという統計量が予想通りのF分布に従う統計量であることを示します。
正規性の仮定のもとで成り立つことに要注意です。
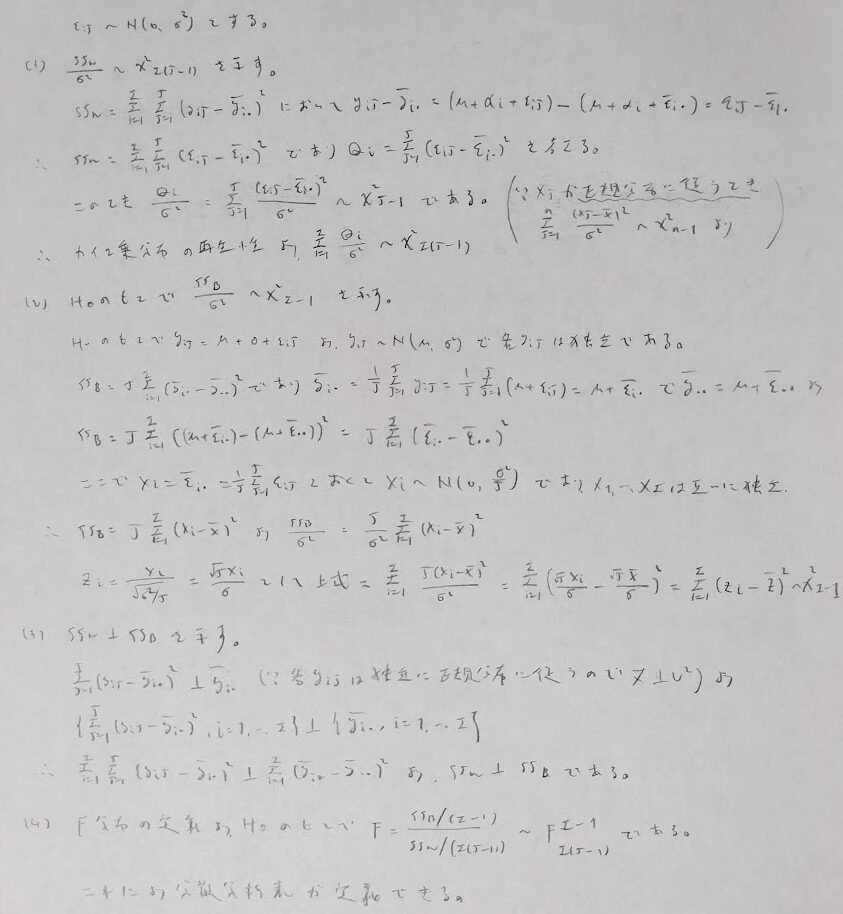
ここで上の内容を一般化させた事柄を考えます。帰無仮説について下記で言及しています。

帰無仮説が棄却された際に、どの組の平均の要因効果が異なったのかを判断したいときの対処法と問題点を考えます。
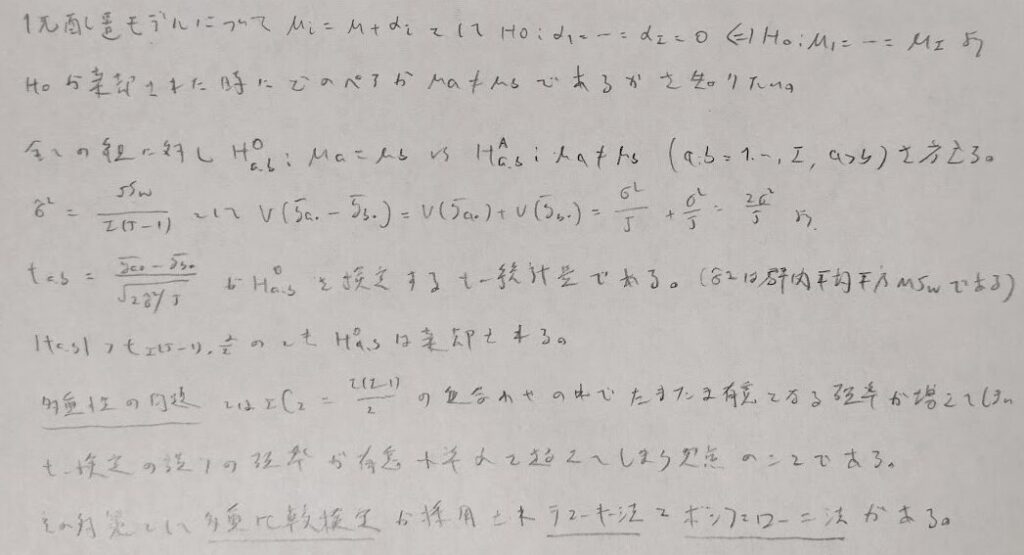
まずはテューキー法を考えます。通常のt検定と比べて棄却されにくいです。
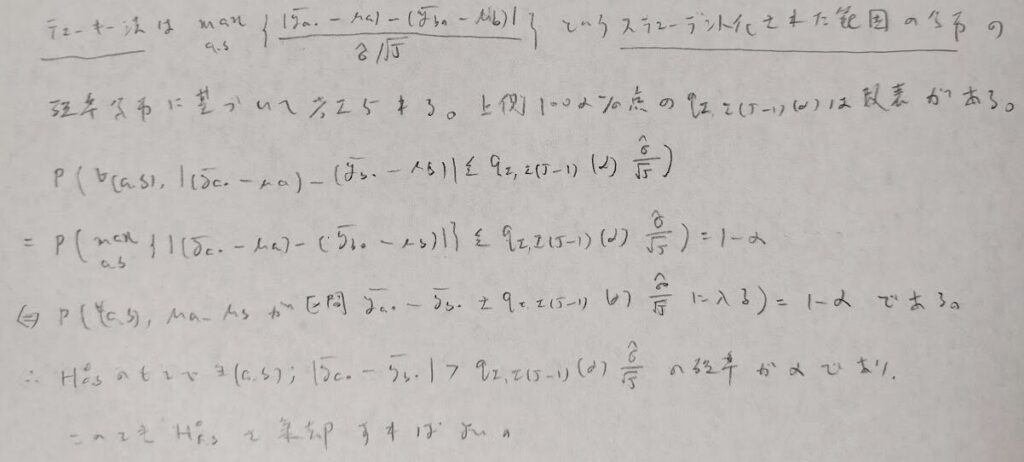
次にボンフェローニ法を考えます。これはボンフェローニの不等式から導き出される方法です。
この不等式が緩いので、通常のt検定の方法より保守的な検定になります。

最後の式でルートの中に2がついているのは、SE(2つの標本平均の差)を考えているためです。
2元配置分散分析
1元配置分散分析の次は交互作用も含めた2元配置分散分析モデルを考えます。ここでも構造式から始まり平方和の分解、そして平方和の期待値を定めて分散分析表を作る意義、そしてF検定に向けた体系立てた内容を追っていきます。
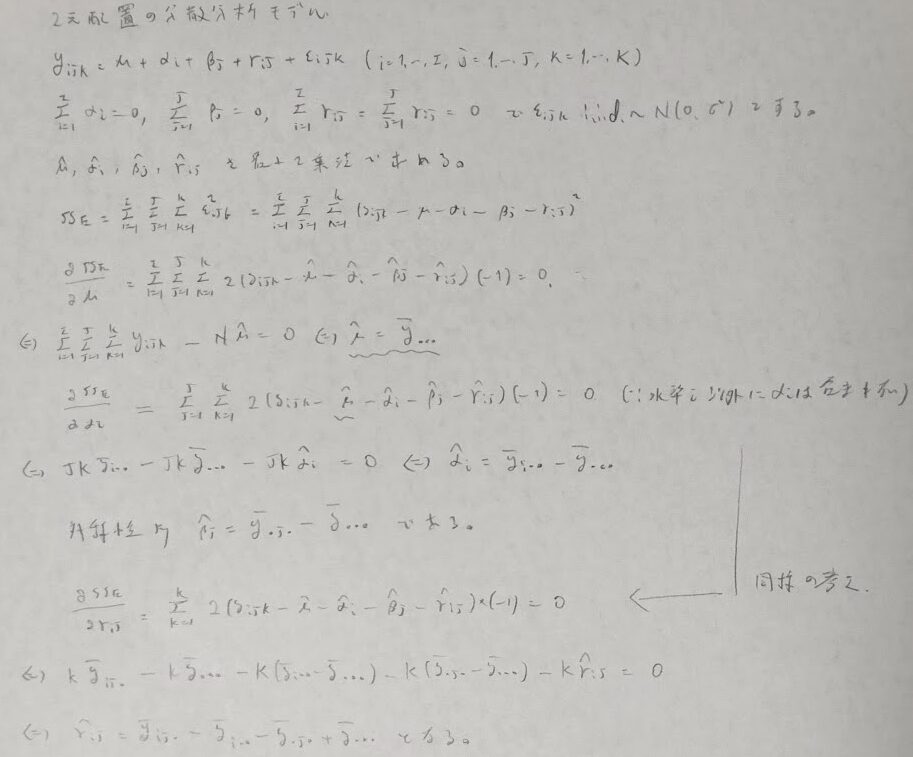
次に平方和の分解を行います。一般平均や主効果や交互作用効果には観測値から得られる推定値を導入して考えます。交差項が0となることがポイントになります。
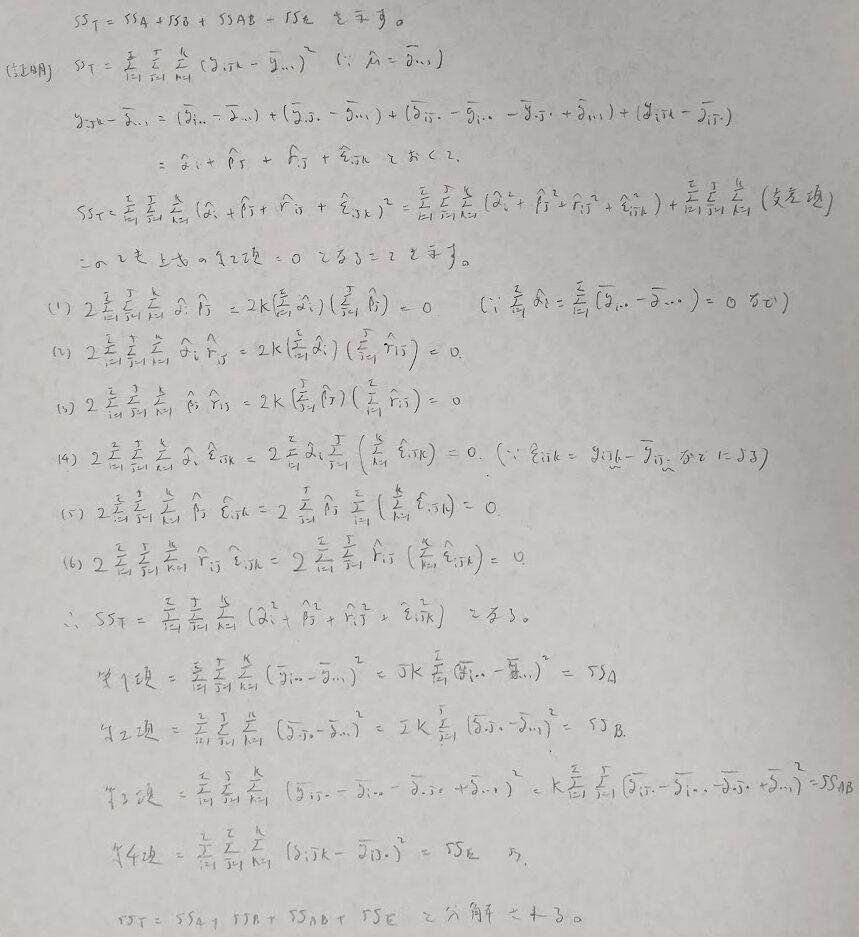
平方和の分解を行ったあとに各平方和の期待値を計算します。その結果、分散分析表に記入すべき事柄が少しずつ見えてきます。

僕はSS_ABの期待値計算でかなり回り道をしていると思い、Xで別証があると思い有識者の方々へ問いかけをおこなっています。この記事をお読み方もエレガントな解法をご存知でいたらご教授くだされば幸いです。
先ほどの証明でとある補題を用いました。その補題を下記に掲載します。
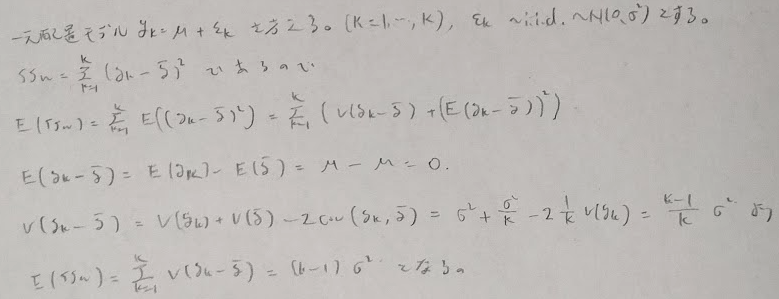
とても細かいことだと思いますが、上の図では僕は1元配置モデルの一種としましたが、主効果が1つもないモデルなので0元配置モデルと考えた方が良い気がします。しかし0元配置モデルという用語は一般的ではないため、1元配置モデルの特別な場合とみなしました。水準が1つのためα_1=0(通常の制約条件で合計値が0の意味)となり、確かに1元配置モデルの一種とみなせるからです。
平方和の期待値の結果を元に、帰無仮説のもとでの平均平方、そして統計量Fを考えることができます。
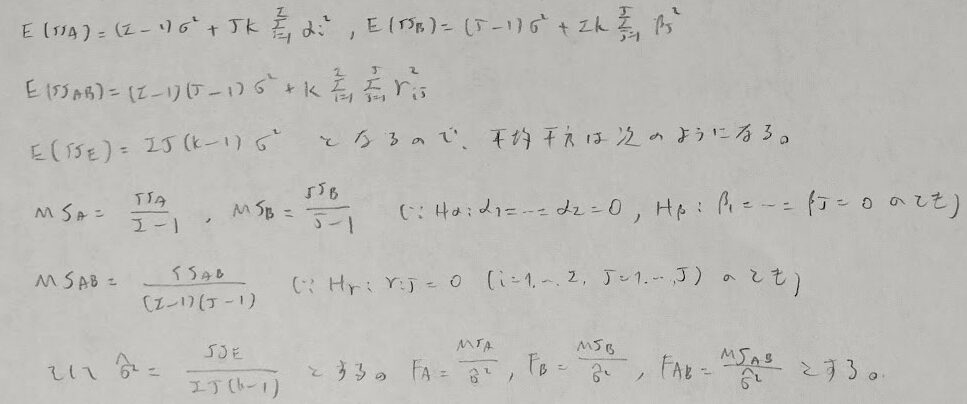
最後に上で定めた統計量Fは予測通りF分布に従います。
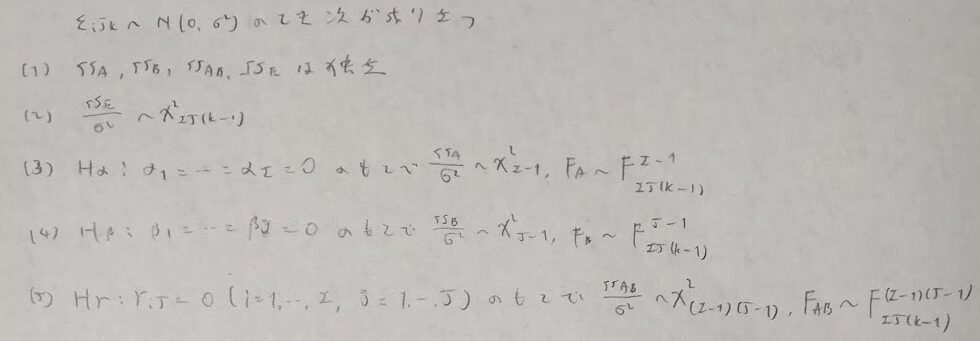
それでは上の命題を証明します。とても量が多くなるので5つに区切って証明します。
(1)はとても難しいので(1)が成立することを前提として残りの証明を行います。
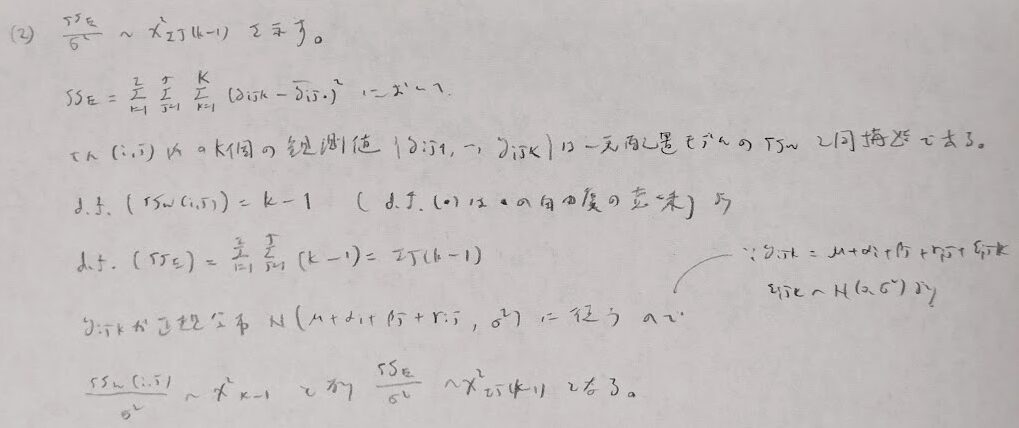
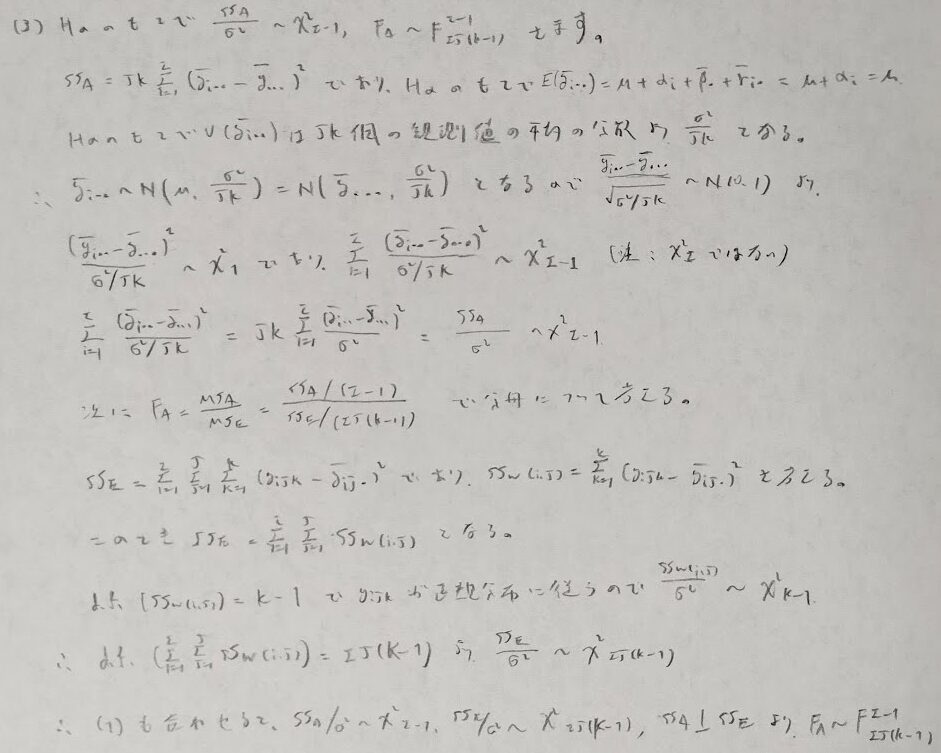

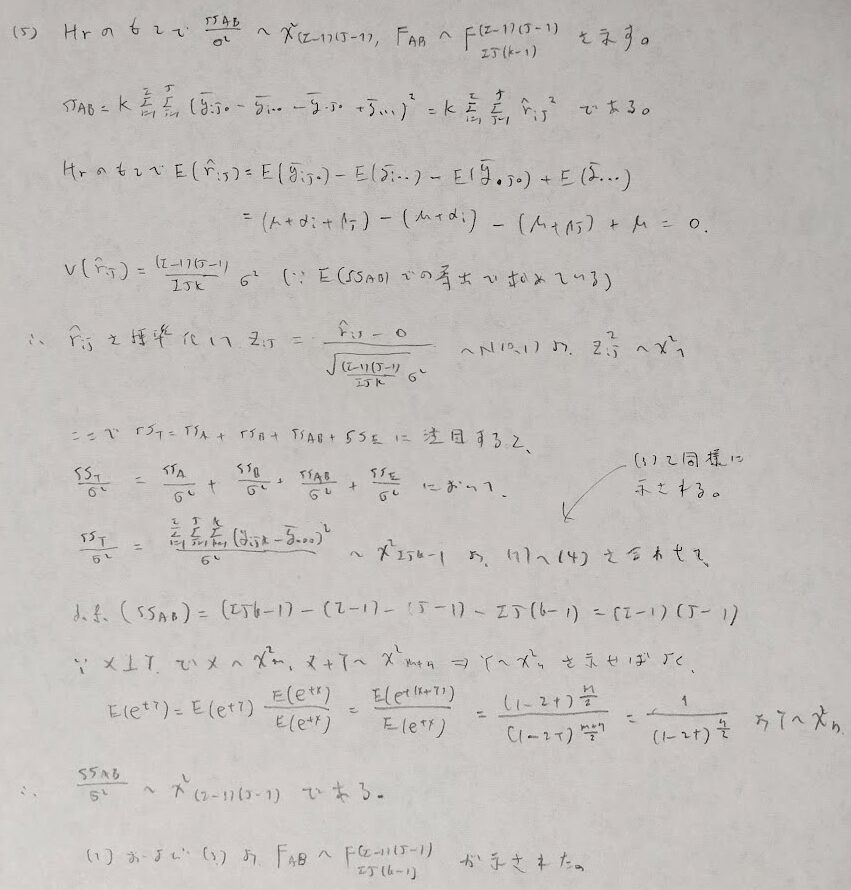
以上で1元と2元配置の分散分析表を用いて解析できる土台が整いました。実際に演習問題で確認していきましょう!
データ解析のための数理統計入門の第15章『分散分析と多重比較』の演習問題
問1:フィッシャーの3原則
フィッシャーの3原則についてAとBの2種類の肥料の効果について3つの実験を行うときに問題点を指摘します。
(1)「農地を2つに分けてどちらかをランダムに選びAを与え、残りにBを与える」この方式は1つしかデータをとっておらず反復の原則に反します。
(2)「実験農地を東側から等間隔に10区画に分けて最初の5区画にAを与えて残りの5区画にBを与える」この方式はAとBの割り付けに系統誤差が生じる可能性があり、無作為化の原則に反します。
(3)「区画内では地力が均質になるように区画を10個選び、その中からランダムに5区画選びAを与えて残りの5区画にBを与える場合」この方式は均質な区画の中にランダムにAとBを割り振ることができていないため、局所管理の原則に反します。
問2:1元配置分散分析モデル

1元配置では群内平方和が残差平方和に相当します。
問3:多重比較の問題
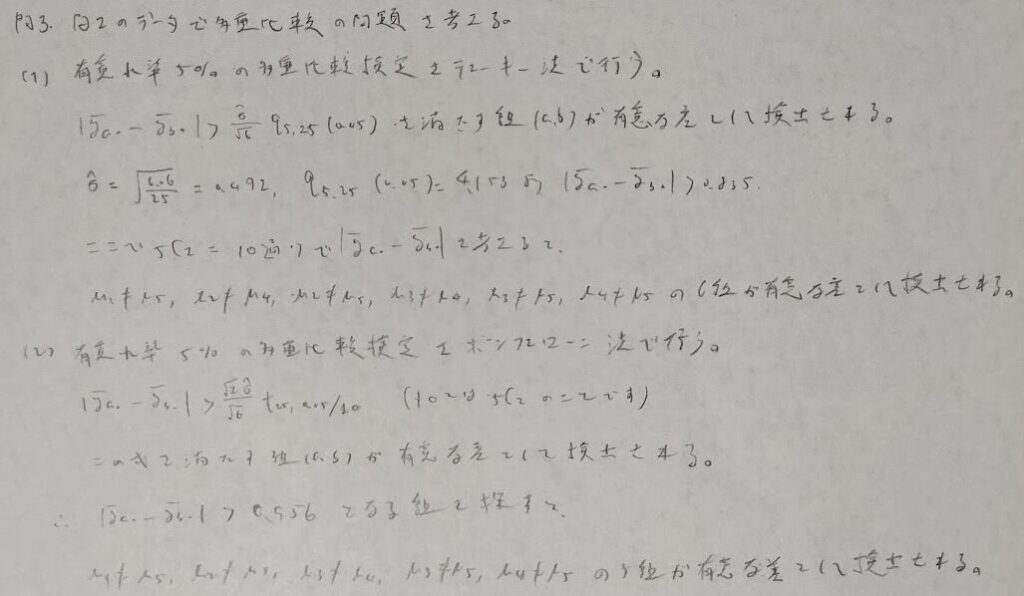
テューキー法とボンフェローニ法での有意差を決める不等式の形は覚えておかないと解けません。なぜこうなるのかは記事の前半の参照をお願いします。
問4:2元配置分散分析モデル

この問題など分散分析表を作れば芋づる式に問題が解けるようになっています。
統計検定1級でもこのような素直な問題が出てほしいところですね笑
本記事では触れていませんが実際の分散分析表を用いた解析では修正項のCTを用いた計算が多用されます。統計検定では計算スタイルとしては見かけないもののQC検定ではなんと2級から計算範囲となっています。僕は2025年9月の第40回のQC検定2級に合格できたため対策として書いた記事内にCT計算を詳しく解説した内容も入っております。よろしければ併せてご覧くださいね!




