離散型確率分布界隈で最後まで生き残っいた四天王がいました。
4つも確率分布がタイトルにありますが一体なにごとですか?!
統計検定1級で出題される離散型確率分布は超幾何分布までで出尽くしました。しかしアクチュアリー数学ではそれに関連する離散型確率分布も出題されます。ただし対数級数分布は除きます。今回の参考資料は『アクチュアリー試験 合格へのストラテジー 数学 第2版』をベースに記事を構築しています。
超幾何分布までが実質的な離散型確率分布の内容ですが、関連する内容も勉強しておくことにより、理解が深まるものです。難易度が低い順に解説していきますが、説明の流れ上、単位分布とデルタ分布は登場の順番を逆にしています。
ベルヌーイ分布よりも単純なデルタ関数由来のデルタ分布と単位分布の期待値と分散を計算します
デルタ関数というものを知っていますか?
確か1点しか取らない特殊な関数でしたね。
線型代数ではディラックのデルタ
フーリエ解析ではデルタ関数というものが大事な役割を演じます。
デルタ関数については『フーリエ解析キャンパス・ゼミ』に分かりやすく書かれています。
フーリエ解析が数理統計学と関係しているのですか!
数理統計学で出てくる特性関数というものが、フーリエ解析学におけるフーリエ変換に対応する概念です。特性関数については論理色が強いため後日紹介します。
デルタ関数を元に考えられる分布をデルタ分布といいます。
Xが平均αのデルタ分布に従うとき、Xはx=αでのみ1という値を取る確率分布を持ちます。このことをX~δ(α)とします。
またα=0のときのデルタ分布を単位分布と呼びます。『リスクを知るための確率・統計入門』の説明を参考にしました。
ベルヌーイ分布ではxが0か1の2点のみを取る感じだったのに、デルタ分布は1点しか取らないんですね笑
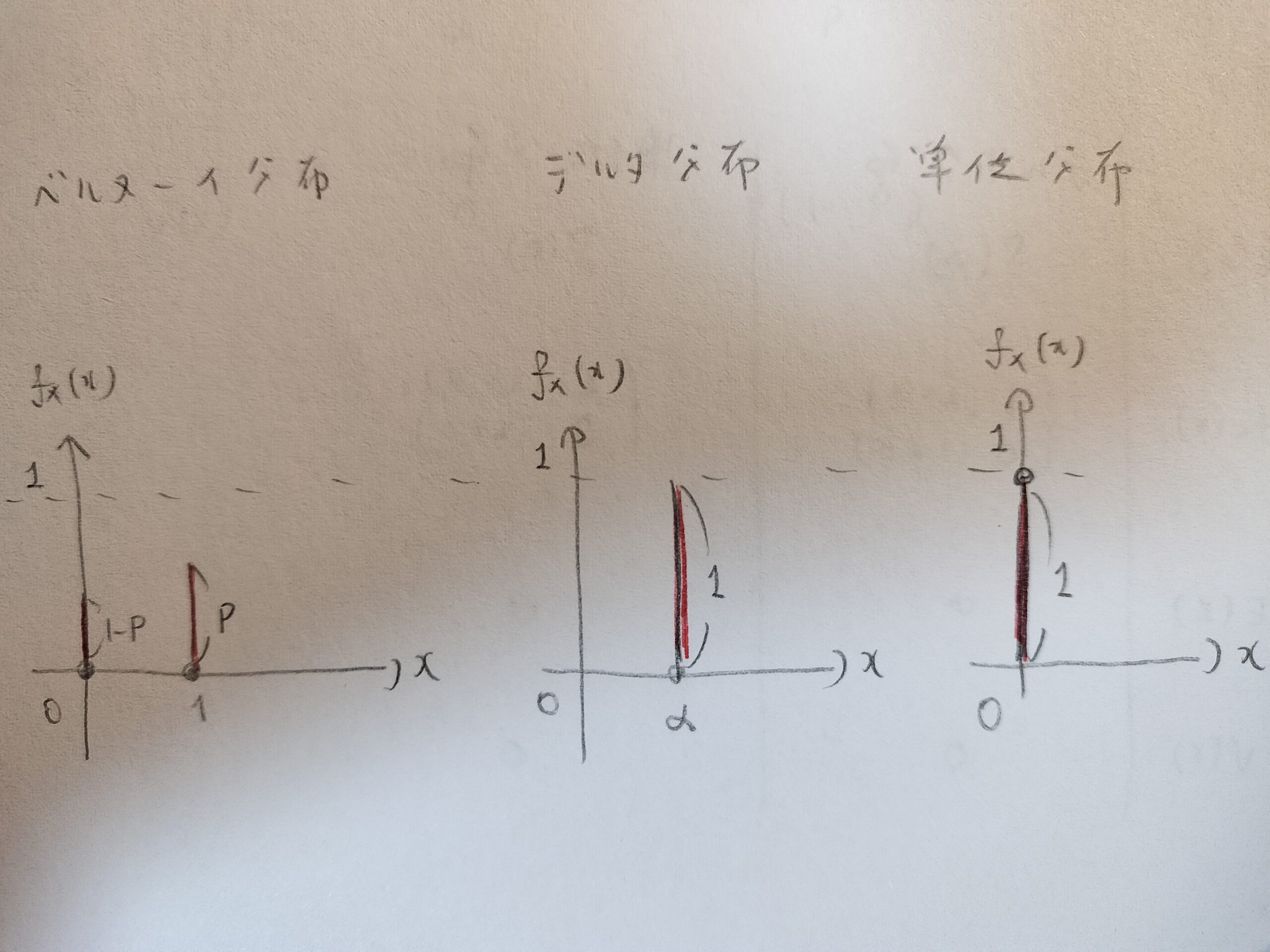
ベルヌーイ分布→デルタ分布→単位分布の確率分布の様子を図示してみました。右に行くほどシンプルな図になっていくことがお分かりだと思います。
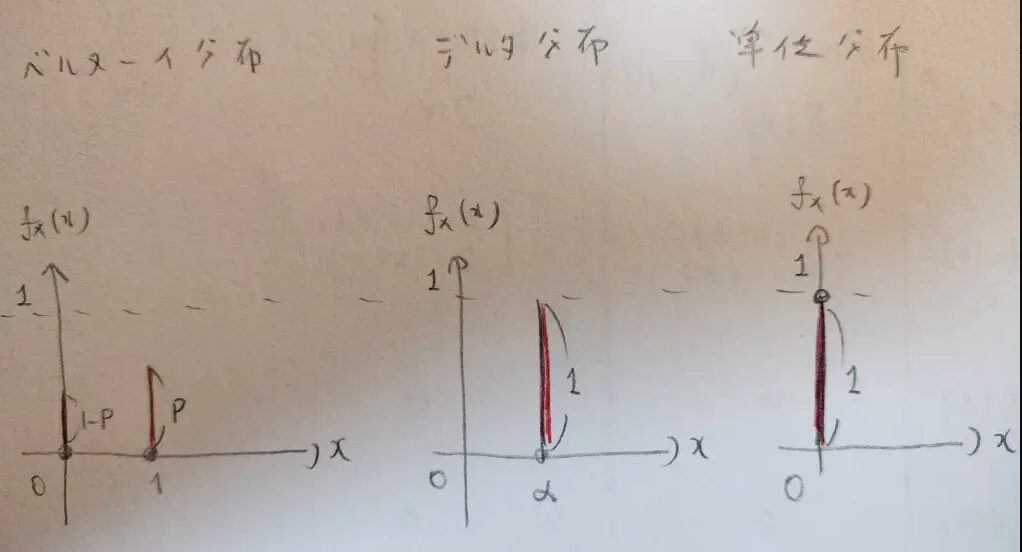
デルタ分布は1点しか取らないので、そこの場所が期待値そのもののはずです。
そして分布のバラツキを表す分散ですが、もはや1点しか取らないので分散は0のはずです。
ここまでの内容を表にまとめてみました。
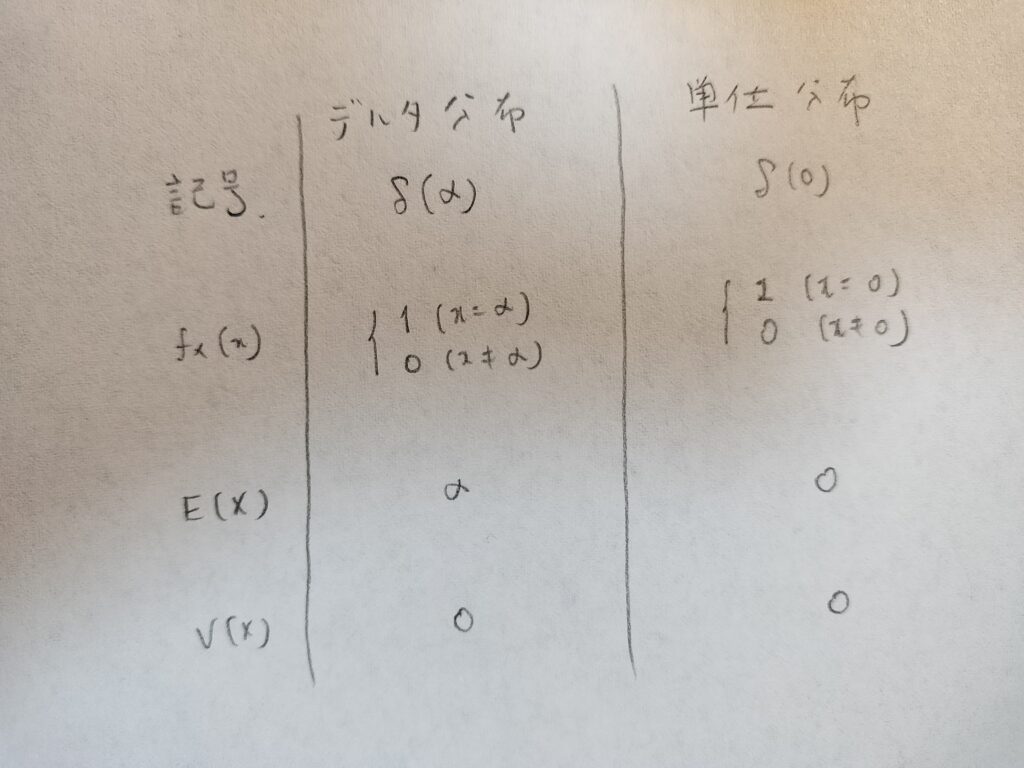
では実際に計算をしてデルタ分布の期待値と分散を確かめてみましょう。
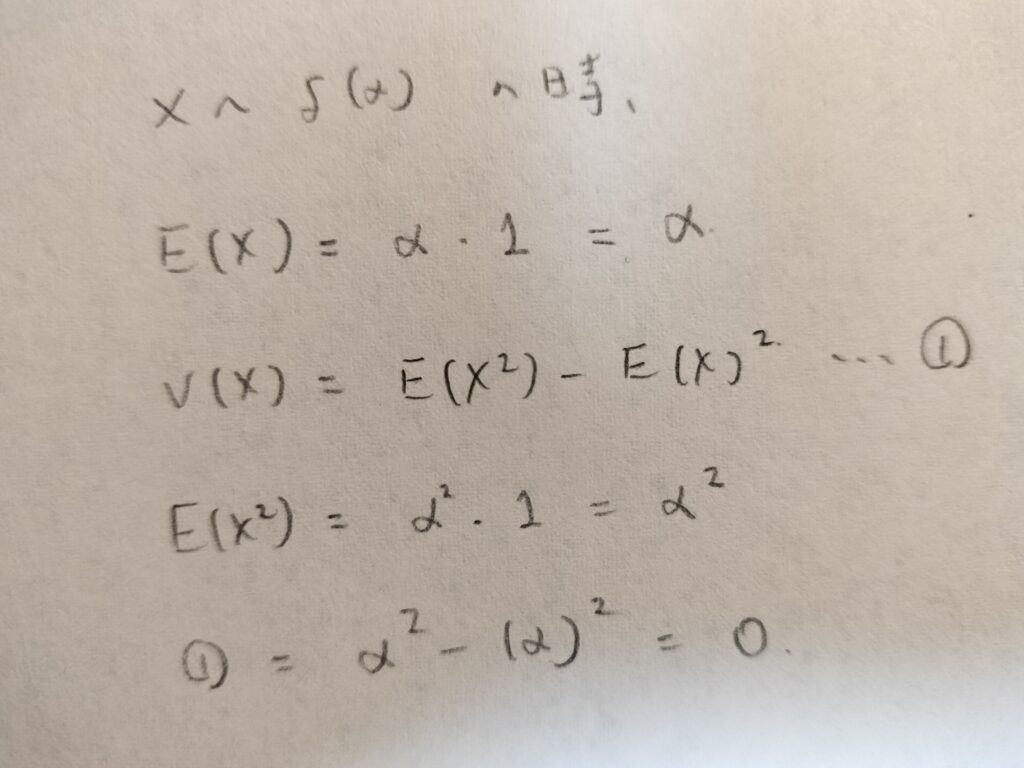
期待値の定義に従って計算する良い例題だと思います。明らかに確率和は1ですね。
単位分布はαを0にすればOKですね!期待値も分散も0なんてシンプル過ぎた結末ですね。
最後にベルヌーイ分布とデルタ分布の期待値と分散をまとめておきます。
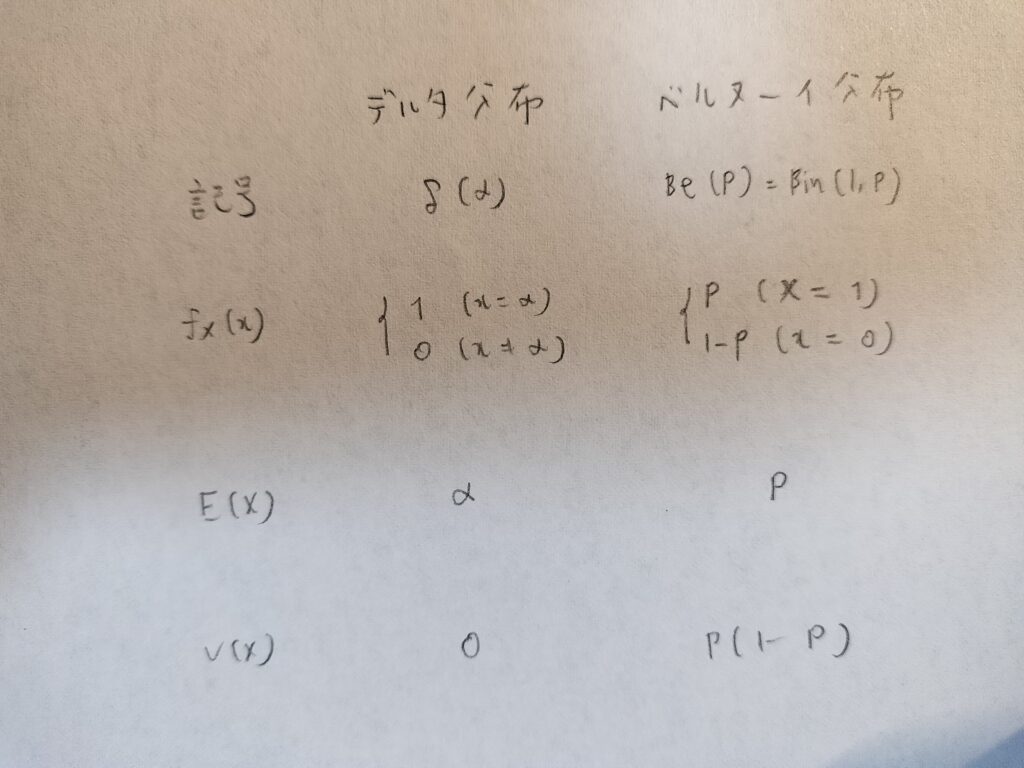
幾何分布を違う角度からみた分布のファーストサクセス分布の期待値と分散を計算します
幾何分布はどういった分布かは覚えていますか?
Xがパラメータpの幾何分布Ge(p)に従うとき、Xが初めて成功するまでに失敗した回数を表す確率変数でした。
これを図で考えたらこのようになります。
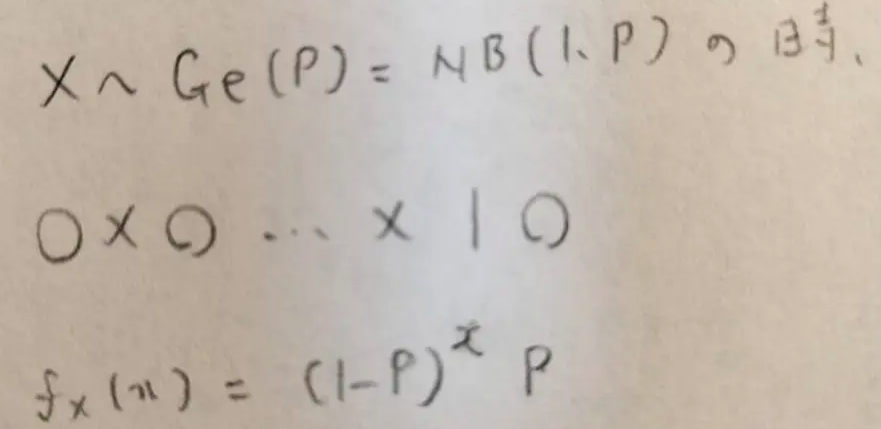
ではこれと同じ状況で、別の見方をしてみます。確率変数Xを初めて成功するまでに要した回数と定義するとき、Xの従う確率関数を考えてみます。
このお話は統計検定1級では見かけることはほぼなく、アクチュアリー数学で多く出題されている分布です。
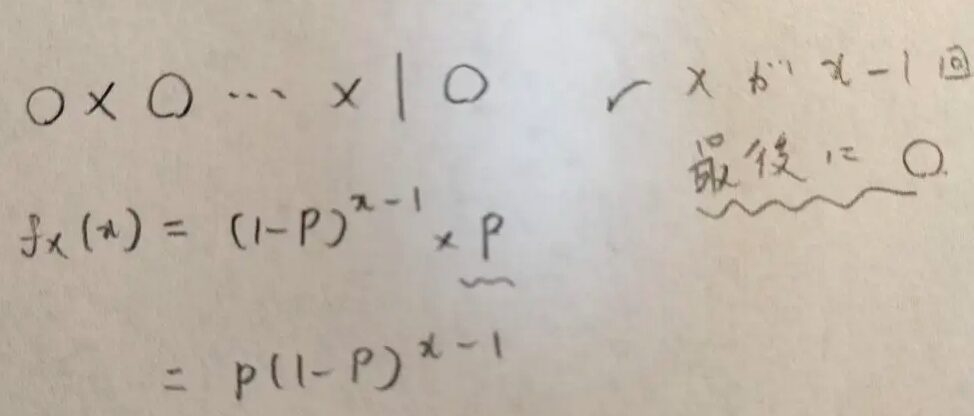
この最後の結果の式にて指数がx-1となっているため、x=1,2,3,…となることに注意してください。
後で出てくる対数級数分布もxは1スタートです。
x回目に初成功したということは、x-1回失敗した直後での成功したということです。受験数学で勉強した反復思考の確率で順番が決まっているタイプの問題ですね。
ではファーストサクセス分布を定義します。先ほどの幾何分布と混同しないため、いったん確率変数をYと置きます。
確率変数Yを初めて成功するまでに要した回数と定義するとき、Yはパラメータpを持つファーストサクセス分布に従うといいます。このときY~Fs(p)と書きます。
ファーストサクセス分布の確率和1を証明しておきましょう。
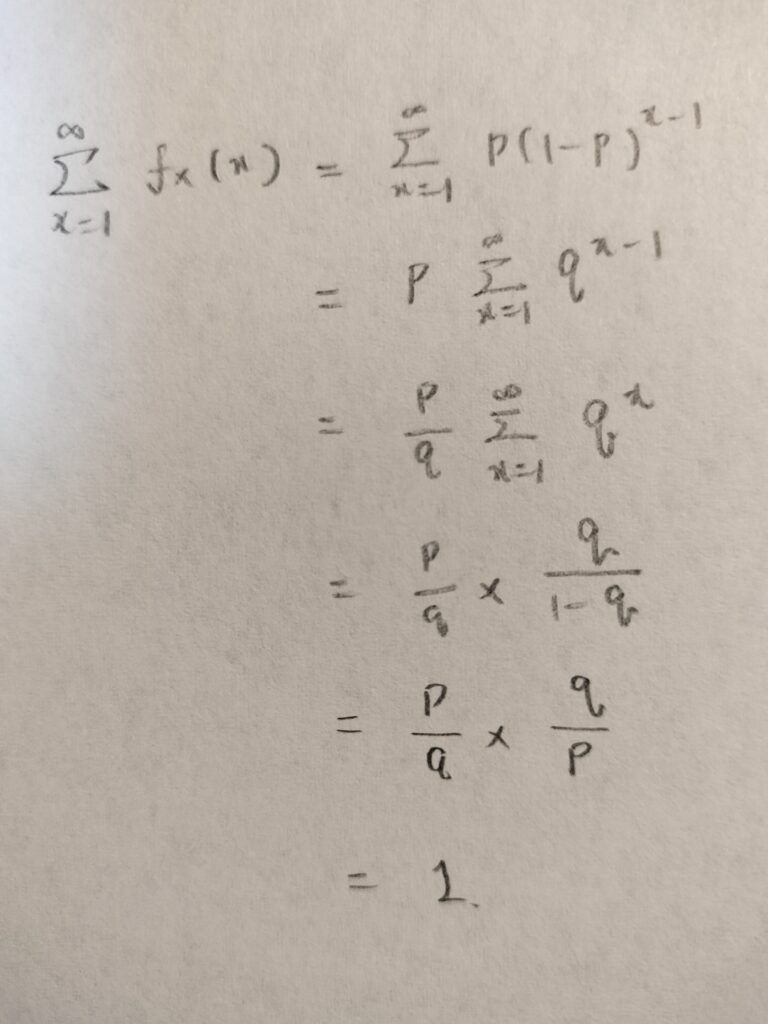
ファーストサクセス分布の期待値を計算する前に、結果を予想してみましょう。
どうやってですか?
こういった時は簡単な具体例で考えると良いです。正確に作られた6面のサイコロを投げる試行を行います。各試行は独立とします。このとき1の目が出るまでの平均回数はいくらでしょうか?
6回の感じがします。
では計算してみましょう。シグマ計算の部分は受験数学で勉強した内容を使います。高校数学Bの等比数列と等差数列の積の和のお話です。
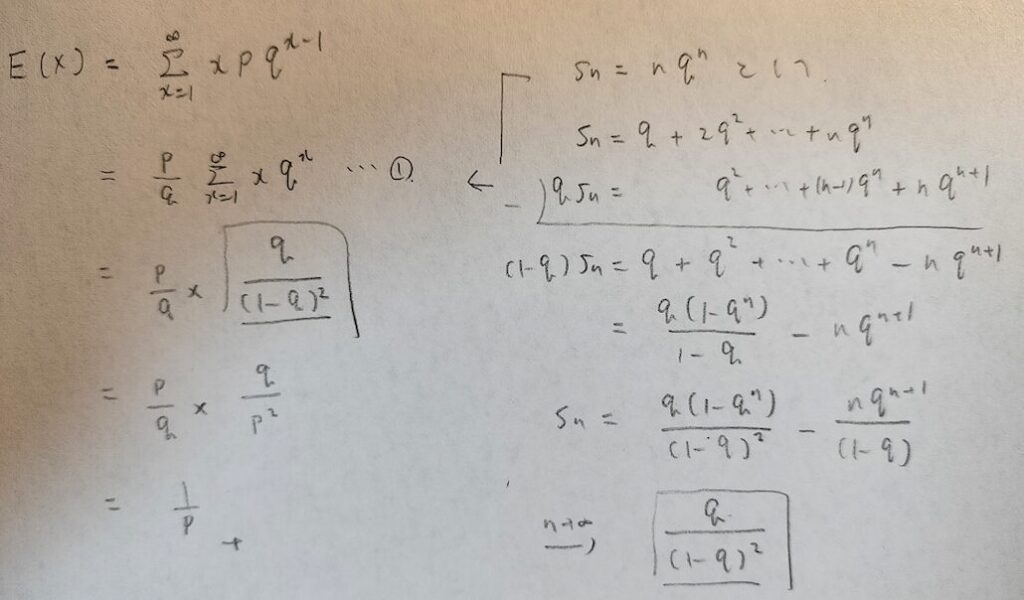
なるほど。さっきの例題ではp=1/6だったので辻褄は合ってますね。
このシグマ計算は正攻法ですが、分散などを求める際は計算量が膨れ上がります。それを防ぐための計算テクニックを紹介します。
では次にファーストサクセス分布の分散を求めましょう。今回も離散型確率分布の特徴である、まずはX(X-1)の期待値を出してみる作戦でいきましょう。微分法を用いて計算量を大幅に省く裏技を紹介します。数学検定1級でよく使われる級数解法の1つです。
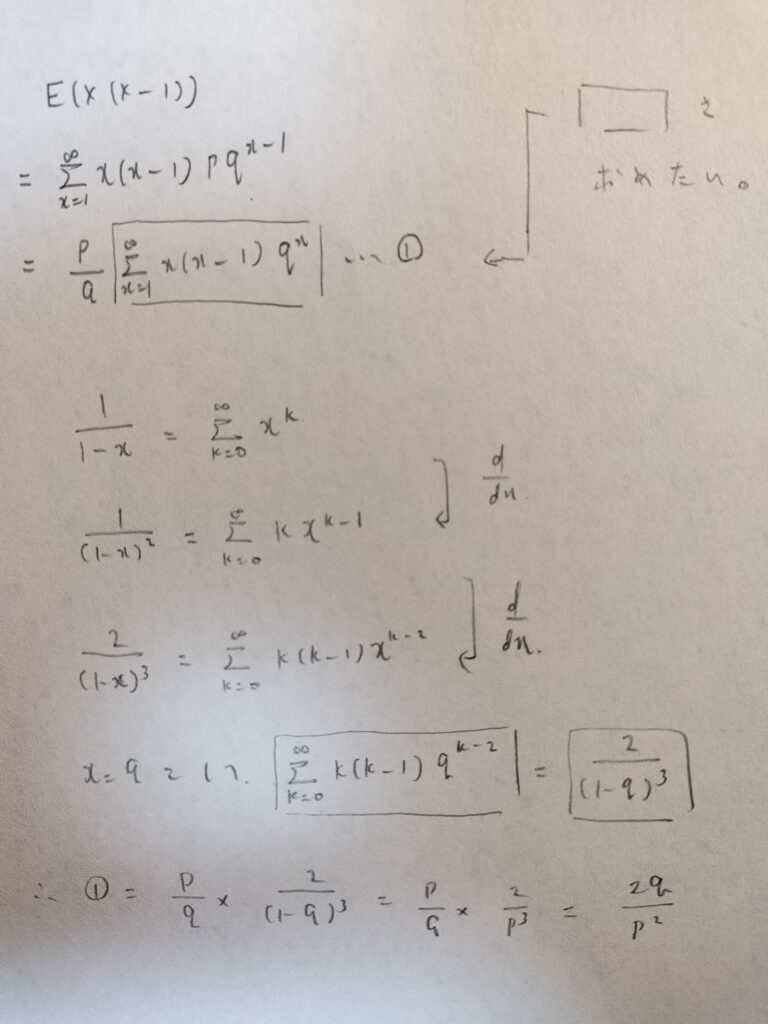
これはすごいです。さっきの期待値の問題も1回微分すれば実質解決しちゃうのですね!
では、最後に分散の計算を仕上げます。
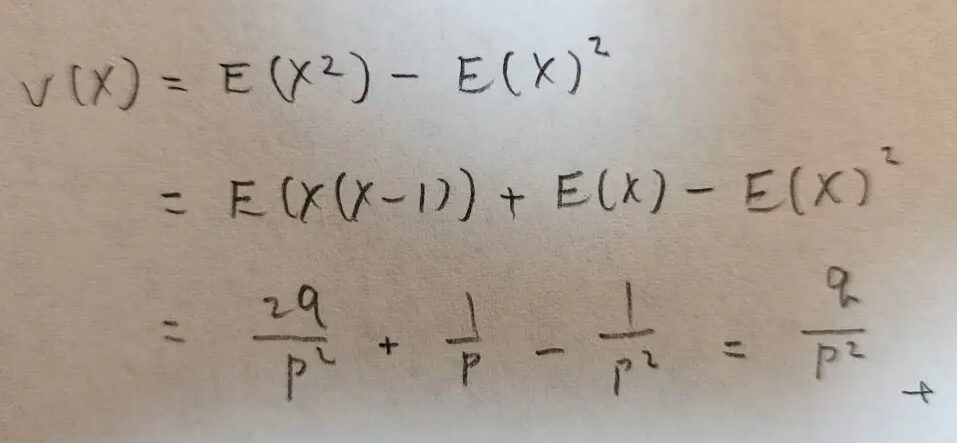
あれ?この結果、どっかで見た覚えがあります。
素晴らしい!実はこの結果は幾何分布の分散と同じ結果なのです。どうしてこのようになるのかを説明します。
ファーストサクセス分布で要する回数Yは幾何分布で要する回数Xよりも1多い状況である事実を考えます。
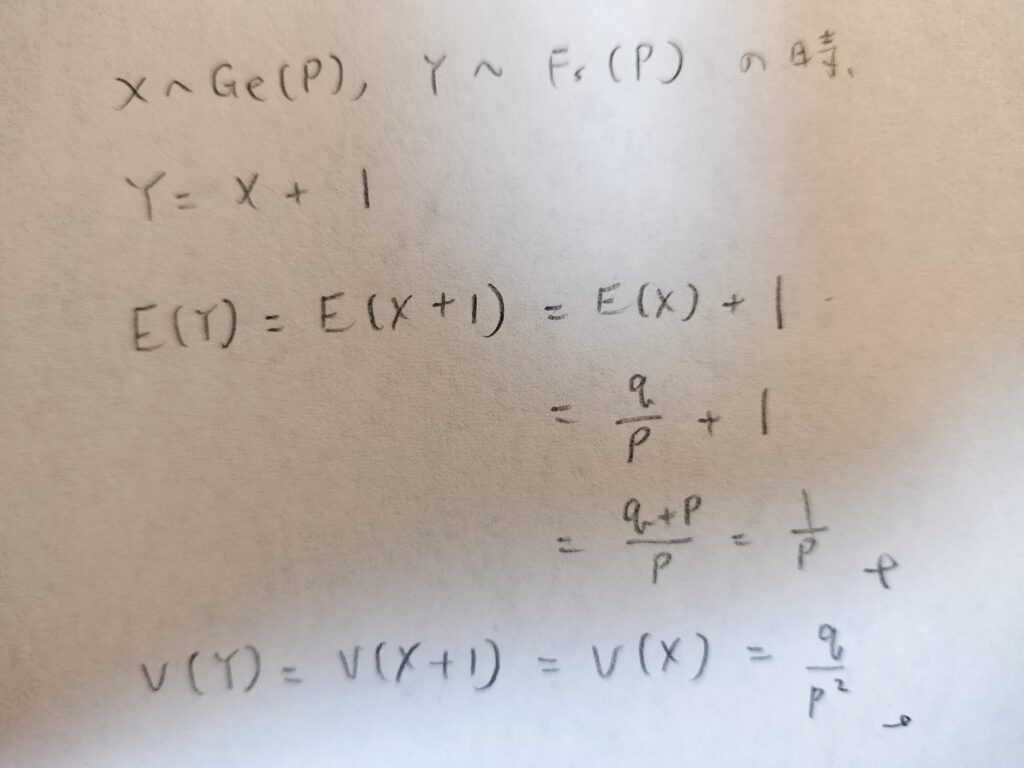
期待値の線形性を用いました。分散では定数の分散は0を用いました。
定数の分散は0は、デルタ分布の内容で勉強したのでOKです。
最後に幾何分布とファーストサクセス分布の期待値や分散関連の性質を比較しておきます。
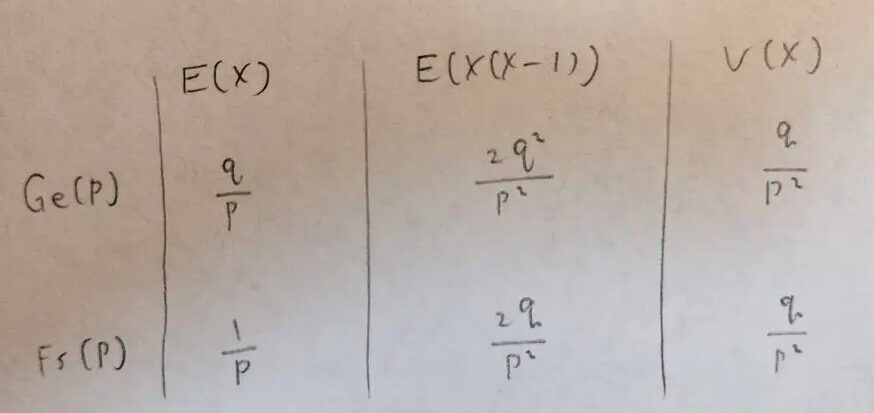
あれだけ式変形をしても、分散がピタリと一致するのは芸術性を感じますね。
対数級数分布(対数分布)の期待値と分散を計算します
幾何分布が離散型確率分布のラスボスなら、対数級数分布が裏ボスに相当します。
そんなに難しいのですか?
統計検定1級の参考書に載っておらず、アクチュアリー数学の参考書『アクチュアリー試験 合格へのストラテジー 数学 第2版』には掲載されているものの、過去問では一度も出ていないという幻の分布だからです。また期待値と分散などが覚えにくい所が裏ボス感を感じます笑
アクチュアリーの損保数理の方で出ているようです。
とても難しい分布なので、ストーリーの流れを大事にしながら順に説明します。
まずは確率関数がどこから出てくるのかを説明します。まずは対数関数のマクローリン展開で有名な公式から始めましょう。これは数学検定1級で良く出てくる有名タイプです。
マクローリン展開については『微分積分キャンパス・ゼミ』が最も分かりやすい説明だと感じました。
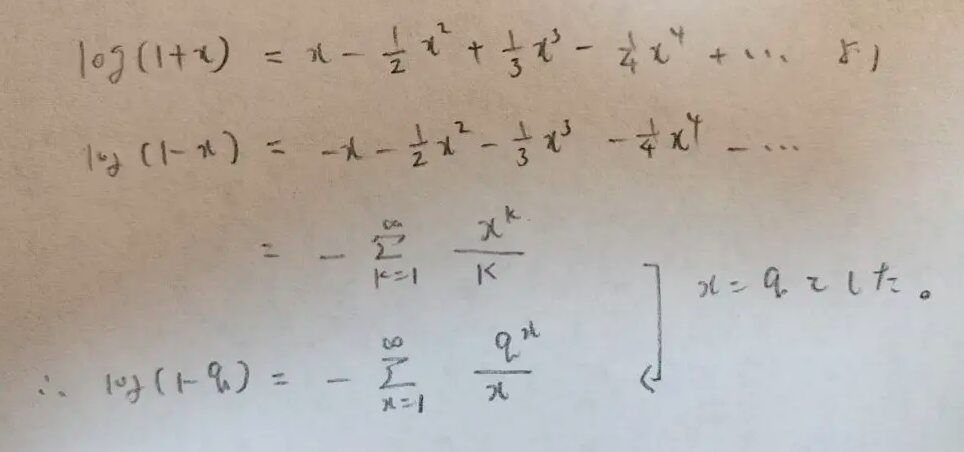
最終的にqという文字を用いています。なぜなら1-qという結果になるので1-q=pと置き換えられるからです。また、最後の式の右辺の形からxは1スタートであることに注意してください。
最後の式の右辺を見てください。これはある確率関数の確率和1に繋げられそうな式をしています。後に登場する不偏推定量を出すときの感覚と似ていますね。そこから確率関数を発見してみます。ここで定数cを設定して以下のように式変形して様子を探ります。
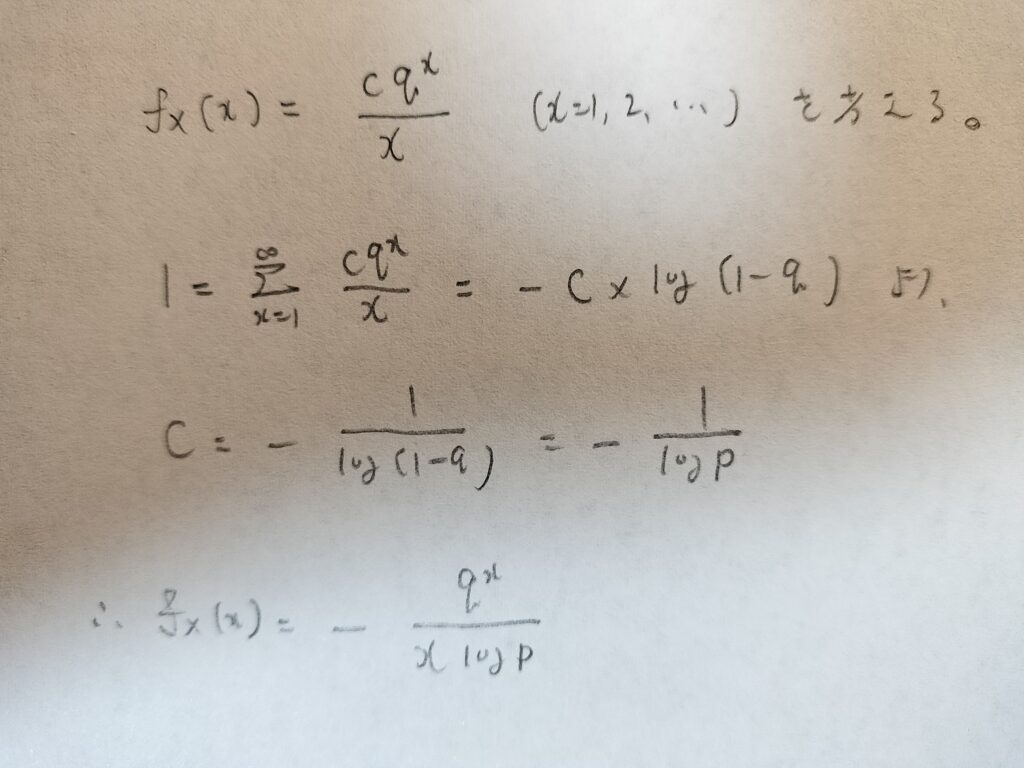
ひょっとして最後の結果が確率関数ですか?
そうです!logがあるので対数分布と呼ばれます。また元々はマクローリン展開(つまり級数が出てきた)ことに注目もしてください。『アクチュアリー試験 合格へのストラテジー 数学 第2版』ではこの確率関数を持つ確率分布を対数級数分布と呼んでいます。
対数級数分布は、Logarithmic series distributionと呼ばれます。パラメータpに従う対数級数分布のことを、英語名の頭文字を持って、X~Ls(p)と書きます。
では対数級数分布の期待値を求めてみましょう。
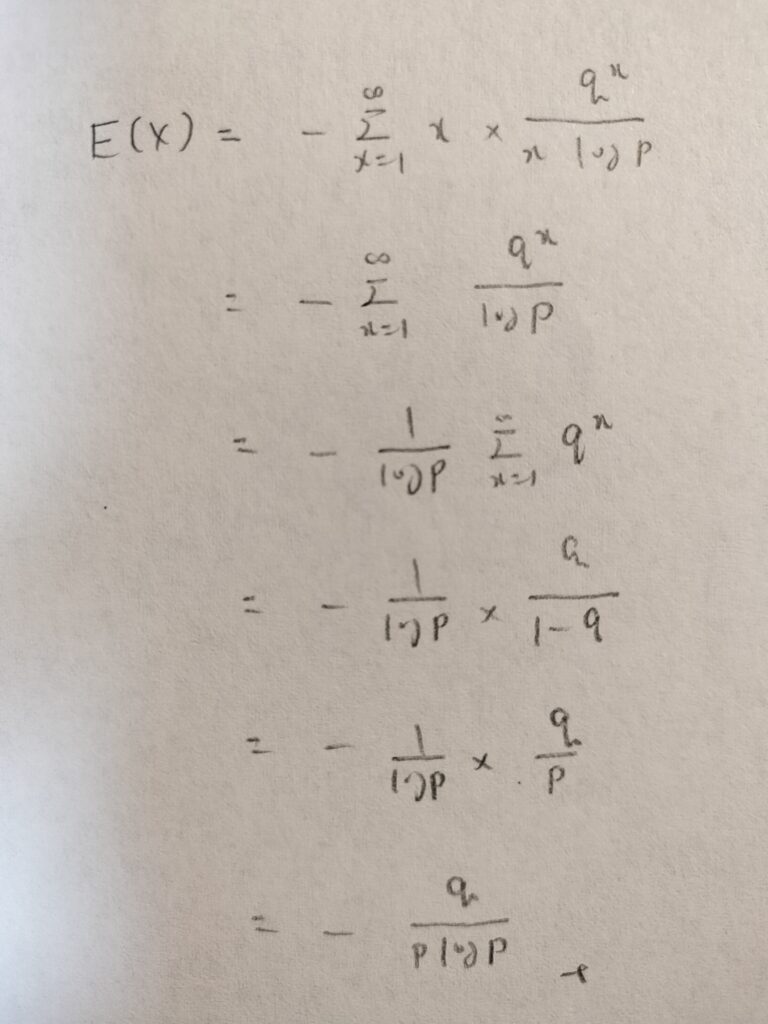
あれだけ難しいと言っていたので身構えましたが、呆気なく終わりましたね笑
そうですね笑。次は分散ですが、これは難しいです。
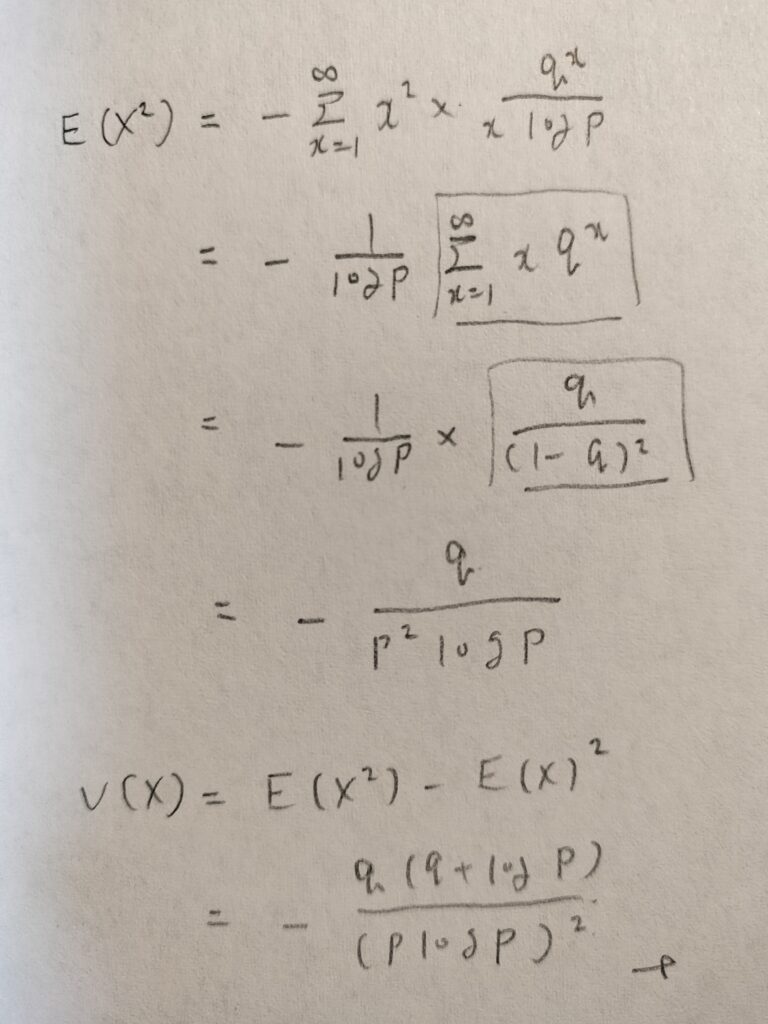
対数級数分布の分散を計算するのが難しい理由は2つありますが、以下を意識すれば乗り切れます。
①対数級数分布は離散型確率変数なのに、X(X-1)の期待値を経由せずにxの2乗の期待値を求めるという連続型確率変数と似たタイプの処理になる。
②上の図で四角で囲った部分でやや複雑な数式処理を行うが、ファーストサクセス分布で紹介した微分を使う裏技をすれば時短になる。
確か「アクチュアリー数学を受験した感覚としては、この分布の分散がどうしても覚えられなくてですね笑」とか言ってましたよね?笑
確かにこのようなことも対数級数分布が難しい1つの理由になっていると私も思います。
実はその欠点を解消する方法があります。
後ほど記事にする積率母関数という手法を用いれば分散の結果それ自体は割とすぐに得られます。
この内容は結果のみ『アクチュアリー試験 合格へのストラテジー 数学 第2版』に載っていました。初見では難しいとは思いますが、離散型確率分布のラストステージとして挑んでみてください。対数級数分布の確率関数の形に習熟できますし、何よりも積率母関数の結果が個人的には覚えやすいと思うからです。
波線部を作れるか?が本質部分です。

積率母関数の結果を覚えていれば期待値や分散の値までは割とすぐに辿り着けます。
E(X)は積率母関数をtで微分した式に0を入れれば求まります。
V(X)は「積率母関数をtで2回微分した式に0を入れた値」からE(X)を2乗した値を引けば求まります。
なぜそうなるのか知りたいです!とても便利そうなので。
積率母関数などの母関数関連はまた後日テーマにします。お楽しみに待っていてください!
最後に単位分布、デルタ分布、ファーストサクセス分布、対数級数分布(対数分布)の内容で参考にした本を紹介します。
対数級数分布の確率分布が登場する根拠の部分である対数関数のマクローリン展開のところで紹介しました。本書は数学検定1級を受験するために僕が初めて購入した大学数学の本でした。当時は中3でしたが、内容が丁寧に書かれていたため、大筋は理解できました。イプシロンデルタから重積分まで載っています。
デルタ関数の説明のところで使用しました。マセマシリーズは本当におすすめです。2023年12月時点での最新刊は『集合論キャンパス・ゼミ』です。
巻末に主要な離散型確率分布と連続型確率分布の期待値や分散などの特性値やコメントが載っています。記事を書く際にも重宝しています。本書はアクチュアリー数学に特化した本です。統計検定1級を目指している方には簡単に感じると思いますので注意が必要です。今回は単位分布とデルタ分布の部分で参考にしました。僕の知る限りだと、単位分布とデルタ分布が詳しく掲載されているのは本書だけです。
ファーストサクセス分布、対数級数分布の全編を通して参考にしました。前半部分は公式が羅列されている印象ですが、ほとんど覚えきれないと問題量の多さに対して時間制限が3時間と短いアクチュアリー数学には合格できません。受験者にはマストの教材です。