統計検定1級の対策書として公式本以外で真っ先に買うべき本である『データ解析のための数理統計入門』の第9章の解説と演習問題を自力で解いた学習の軌跡の記事です。本章は統計検定1級の統計数理に該当する最後の章になります。今までの内容の総まとめ的な内容となっております。
一般的な検定の構成方法(尤度比検定→ワルド検定)→区間推定(ワルド型)→母相関係数の検定と区間推定の順で解説します。前提知識として第8章をお読みになってからの方が理解が深まります。
統計検定1級青本の第9章の説明と例題
P値
まずは検定統計量を定義します。これに基づいて棄却域などを設定します。

また有意水準関連の話題も整理します。特に検定関数は類書にはないですが、これを使うとネイマン・ピアソンの定理の証明がわかりやすくなります。
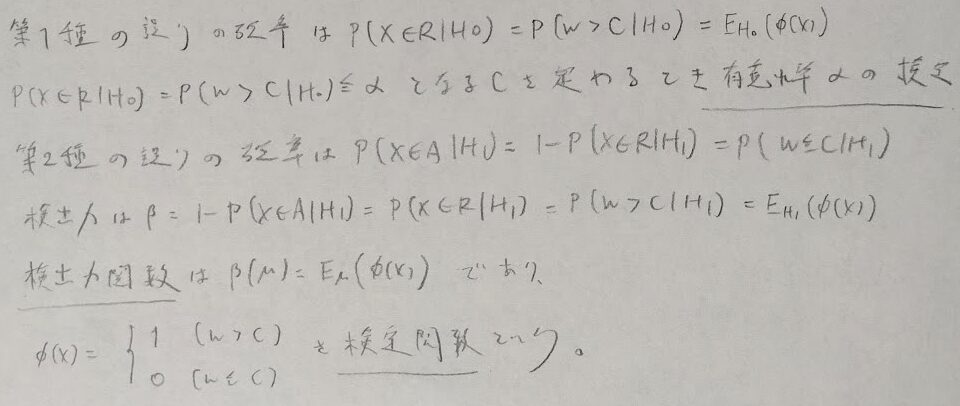
P値に関する定理を紹介します。複雑ですので丁寧に解説しました。P値と有意水準の間の関係式になります。この式からαが求まると思いますが、有意水準は検定開始前に設定しておくので注意しましょう。
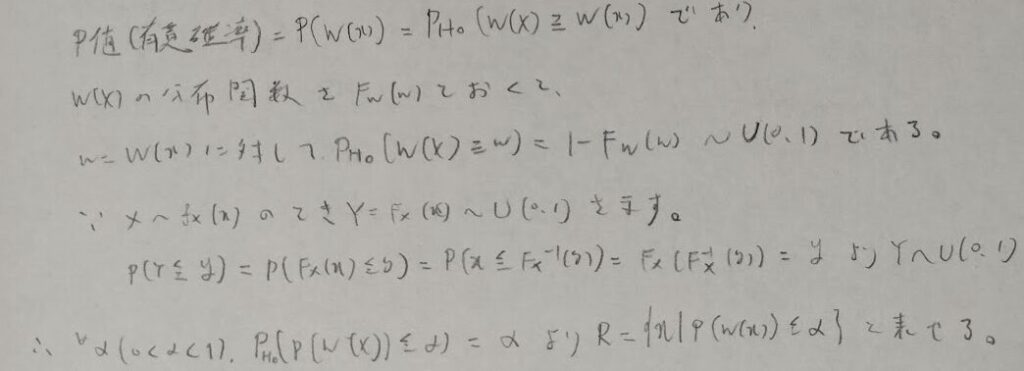
尤度比検定
質の良い検定とは検出力が高くなる検定です。こういった最強力の検定を作るにはどうすれば良いか?を説明したのがネイマン・ピアソンの補題です。1次元のパラメータについての話になります。つまり尤度比検定は最強力検定になります。

尤度比検定が一様最強力検定になるための条件について考えます。ポイントは対立仮説の点が検定に依存するか?というところです。
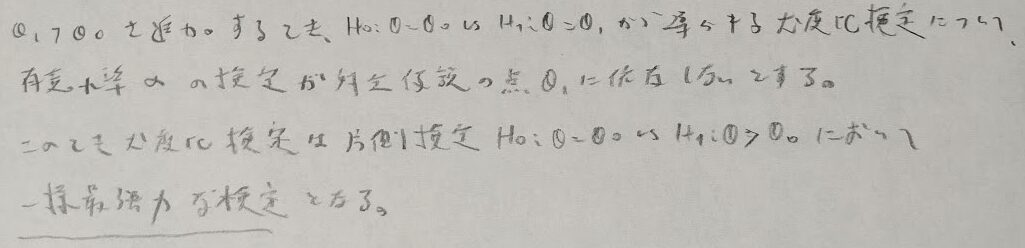
尤度比検定を一般化します。

尤度比検定は何がそんなに嬉しいのか?というと漸近分布がカイ2乗分布に従うことです。
以下の定理をウィルクスの定理というようです。
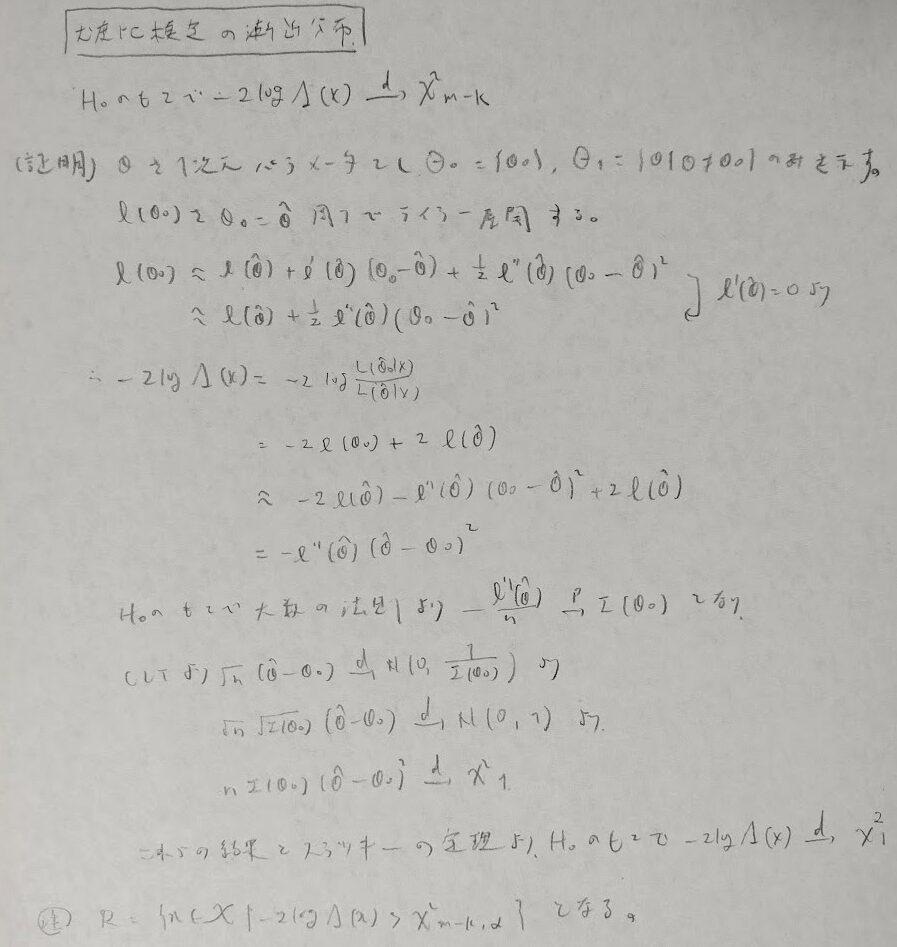
それでは例題を見ていきます。正規分布の場合について例を取り上げます。
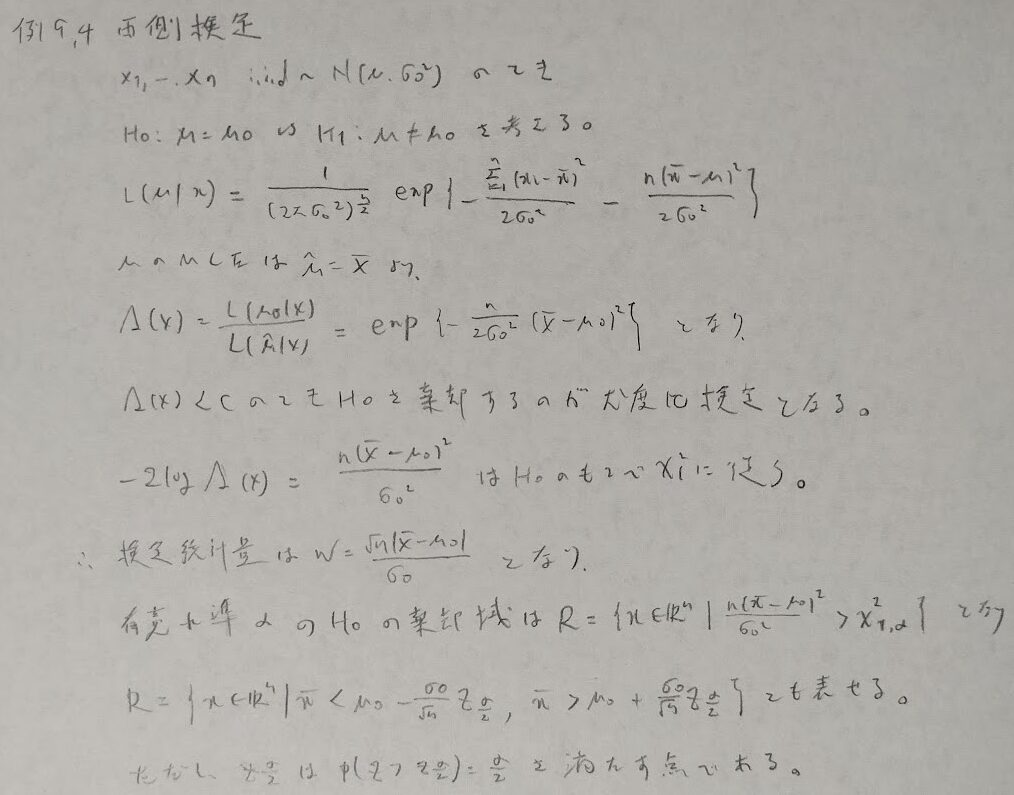
次はt検定に帰着するパターンです。『データ解析のための数理統計入門』には省略されていたところを補いました。
ウィルクスの定理は近似的な棄却域を与えるものです。つまり尤度比検定統計量から直に不等式を作って得られる棄却域は正確なものですが、対数をとってカイ2乗分布に帰着させるパターンでの棄却域は近似的とみなされます。
ここでは正確な棄却域はt統計量が関係していることを前面に押し出して解説しています。

t統計量に関する部分をさらに詳しく解説します。
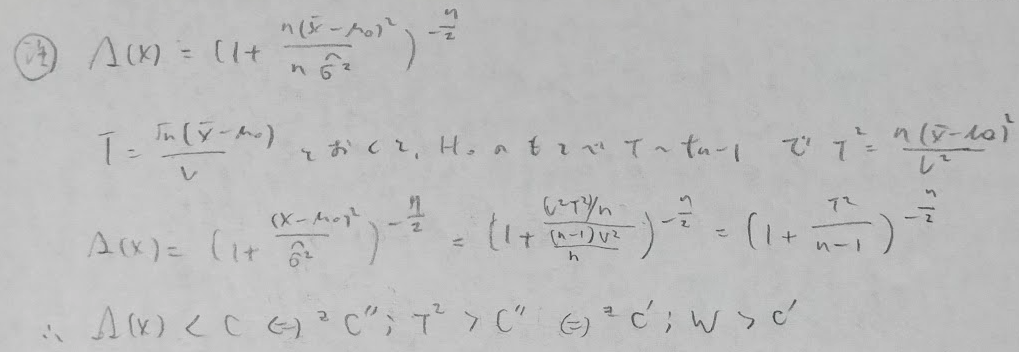
次は平均の同等性検定について触れます。こちらも正確な棄却域の導出にはt統計量の考察が必要です。
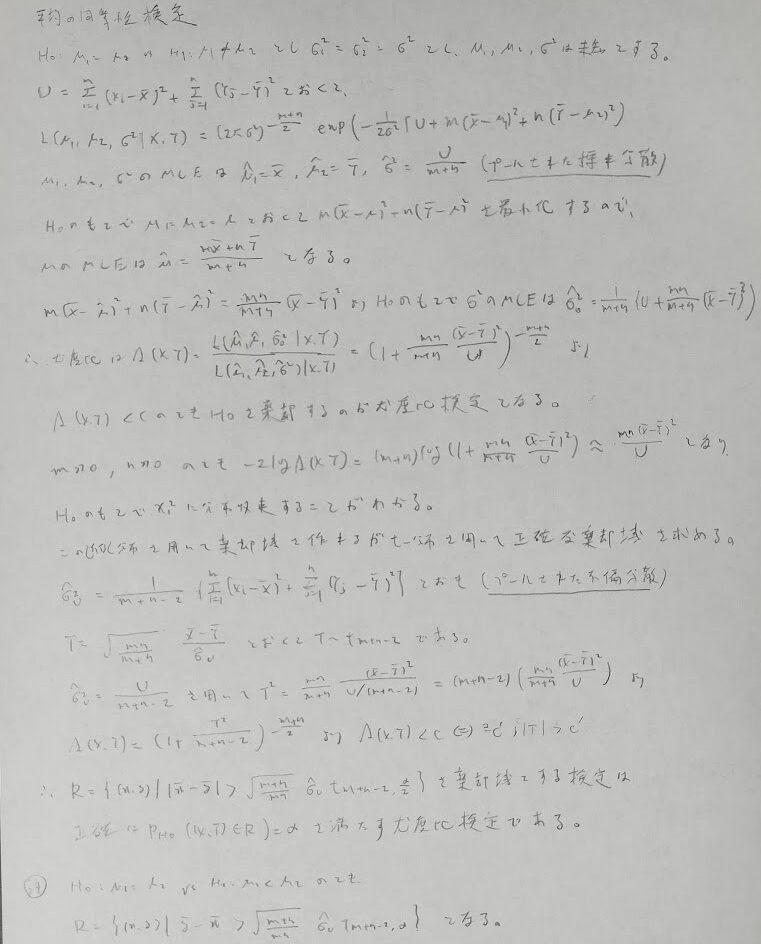
次は分散の同等性検定を考えます。こちらは母分散が同じか異なるか?で難易度が異なります。

次に母分散が同じという条件を撤廃した場合を考えます。これをベーレンス・フィッシャー問題といい、ウェルチの検定を用います。
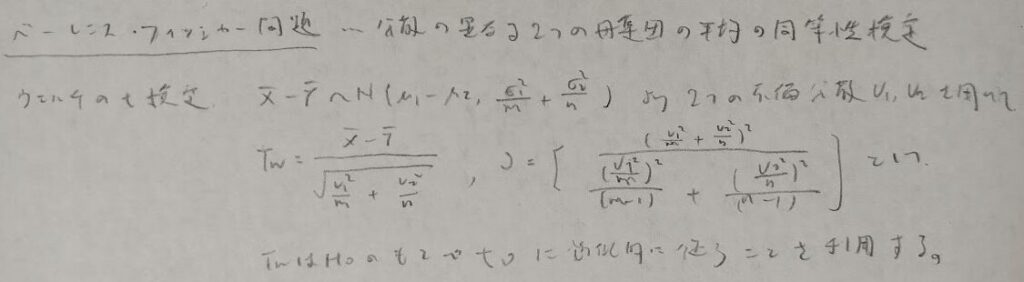
ウェルチの検定はサタースウェイトの方法で求めています。ここまでの深い掘り下げはQC検定1級の範囲になります。
対のあるデータの同等性検定を考えます。こちらは1変数に帰着させることがポイントです。
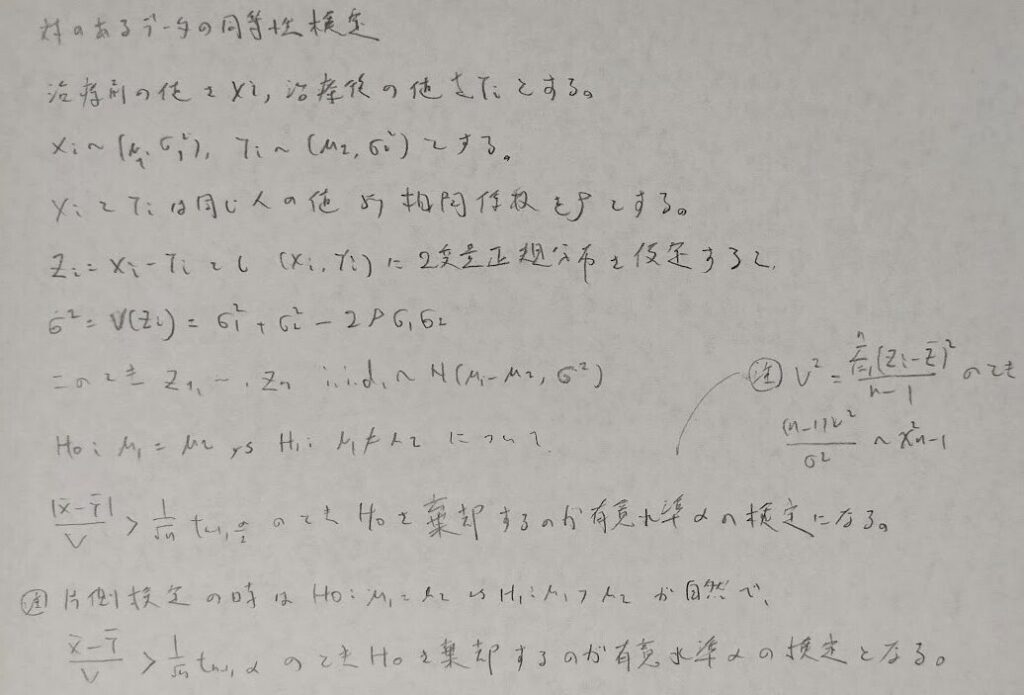
ワルド検定
いよいよ統計検定1級でよく問われるワルド検定について解説します。ワルド検定の構築には2種類あります。確率(密度)関数が与えられている場合は最尤推定量の漸近正規性から考えます。確率(密度)関数が与えらえれていないときは、平均と分散の情報から中心極限定理を用いて考えます。ワルド検定の方法は信頼区間の話題へとつながるので大変重要です。

ベルヌーイ分布を用いた具体例です。
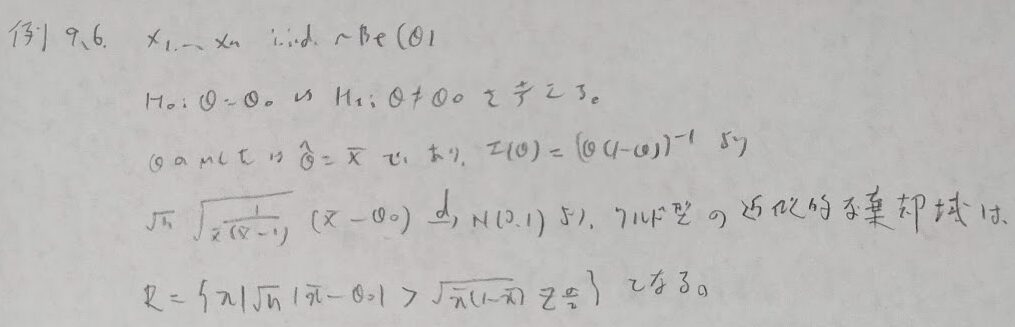
次に確率(密度)関数が不明な場合のワルド検定の構成法について解説します。
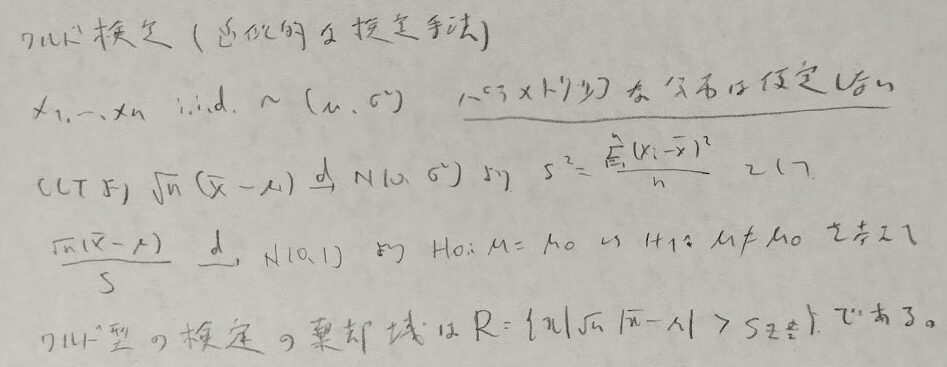
対のあるデータの同等性検定の例で解説します。実際に確率(密度)関数が不明であることに注目してください。

いよいよ終盤です。信頼区間について学びます。ここでは今までのような実現値ではなく、確率変数で表現されることに注意してください。信頼区間は確率変数で考えるためです。信頼係数90%とは、100回検定を行ったときに信頼区間に母数が入っている回数が90回ということです。
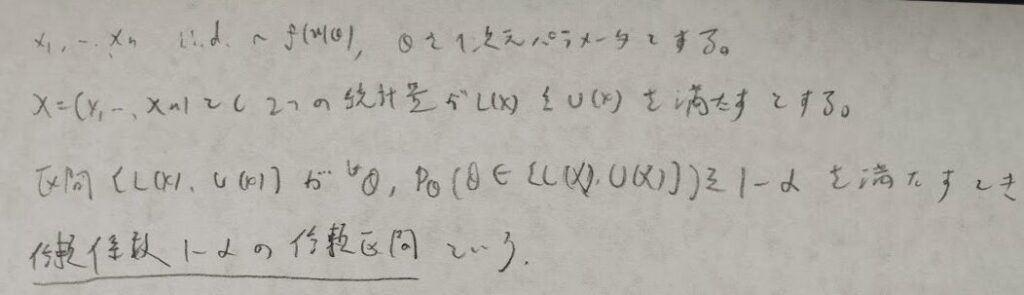
信頼区間の求め方について解説します。棄却域の反対である受容域を求めます。そして受容域の実現値の記号を確率変数に戻して、母数に関する不等式を解くことにより求めることができます。
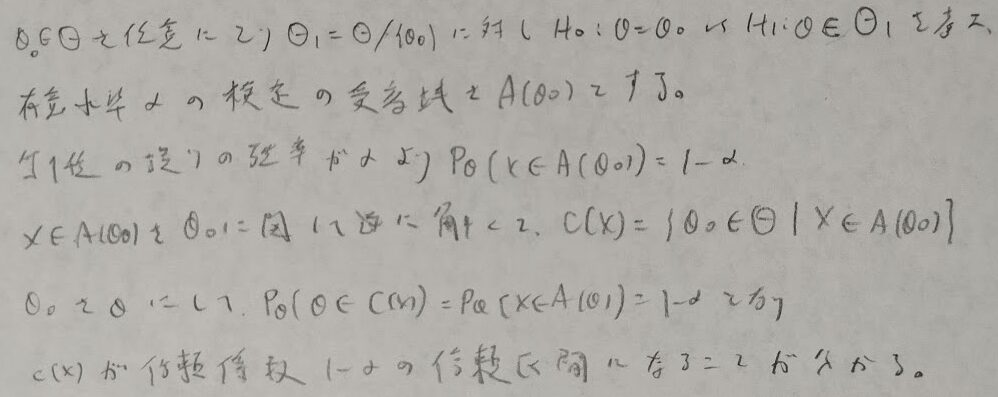
それでは信頼区間に関する例を紹介します。
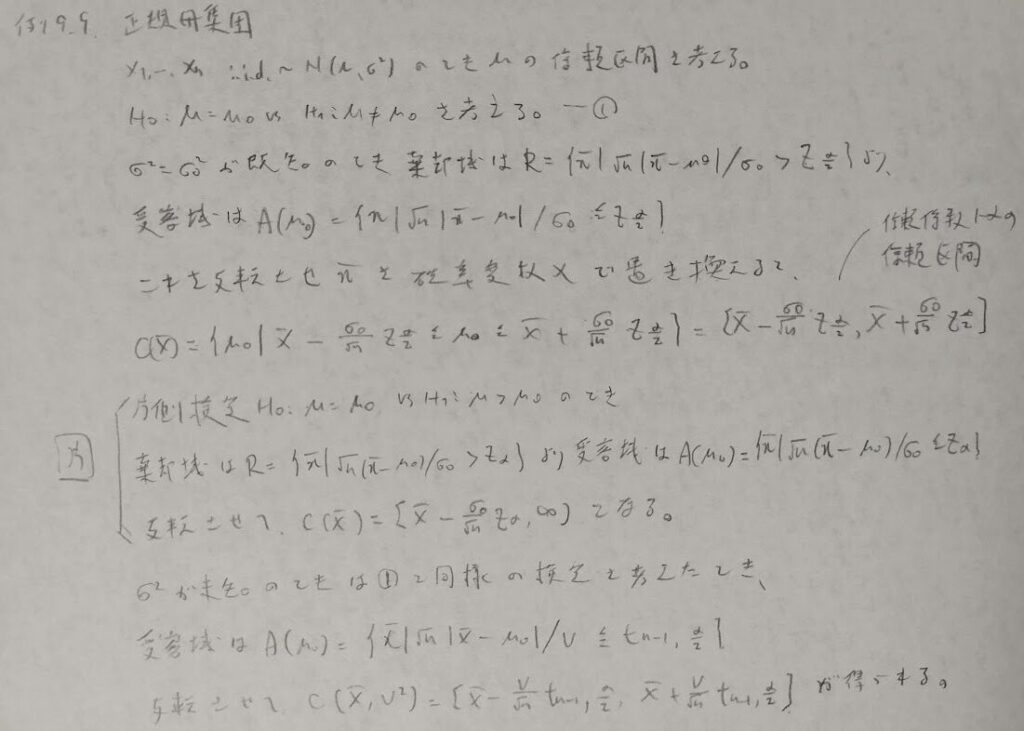
それでは一般の確率(密度)関数が与えられた場合の信頼区間の構築方法について考えます。ワルド検定の方法からスタートします。
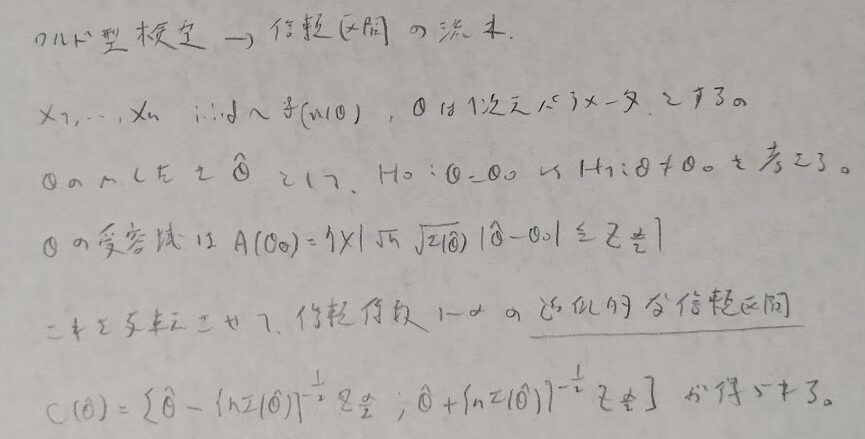
ベルヌーイ分布を用いた例を考えます。
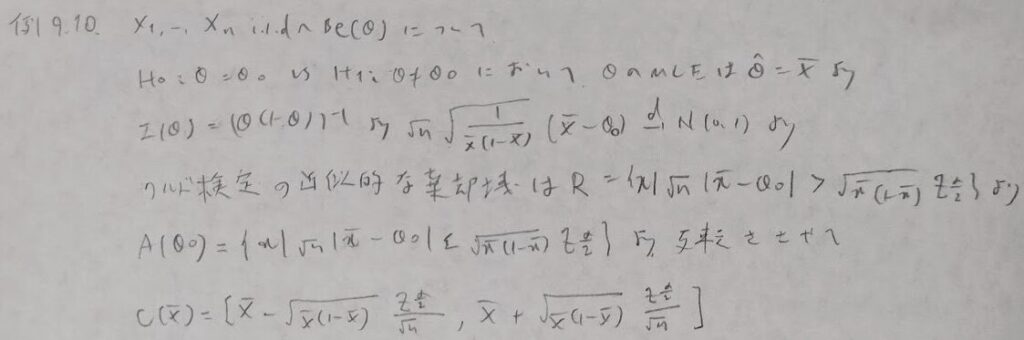
最後に確率(密度)関数を仮定しない場合の信頼区間の構成法を考えます。

対のあるデータの例で解説します。
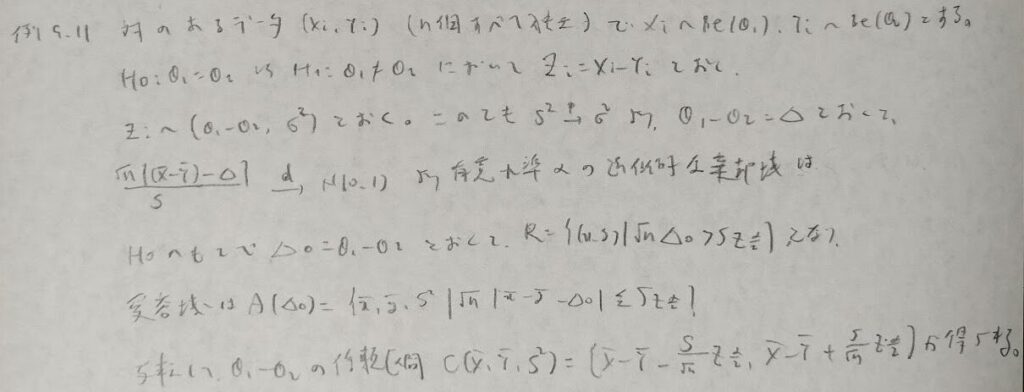
アクチュアリー数学で頻出のサンプルサイズに関する内容にまで言及していきます。一般に標本サイズは標本を取る前に決めるので標本平均の値は未知であることに注意してください。

母相関係数の検定
最後に母相関係数の検定について扱います。ここではサンプル数nが小さい場合のt統計量→nが大きい場合のフィッシャーのz変換の順で学びます。
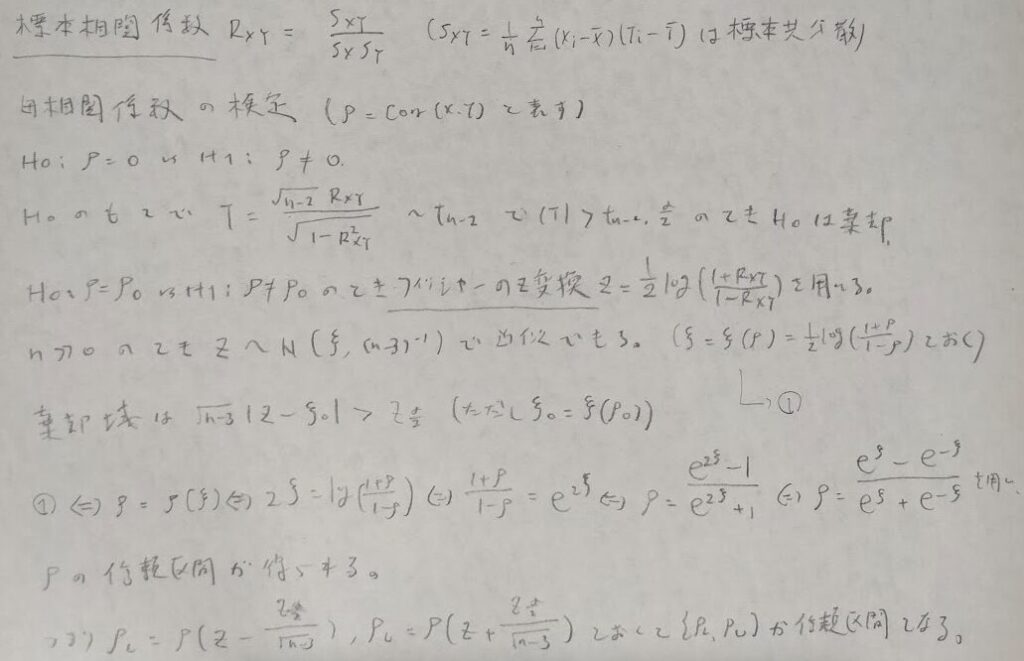
統計検定1級青本の第9章の演習問題
問1:母平均の検定(母分散既知)

問2:指数母集団における母平均の検定
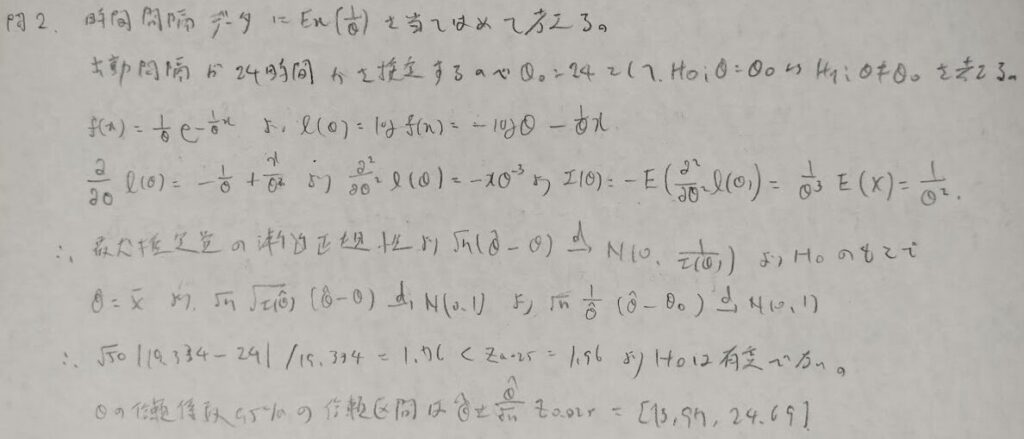
問3:ポアソン母集団のパラメータの検定
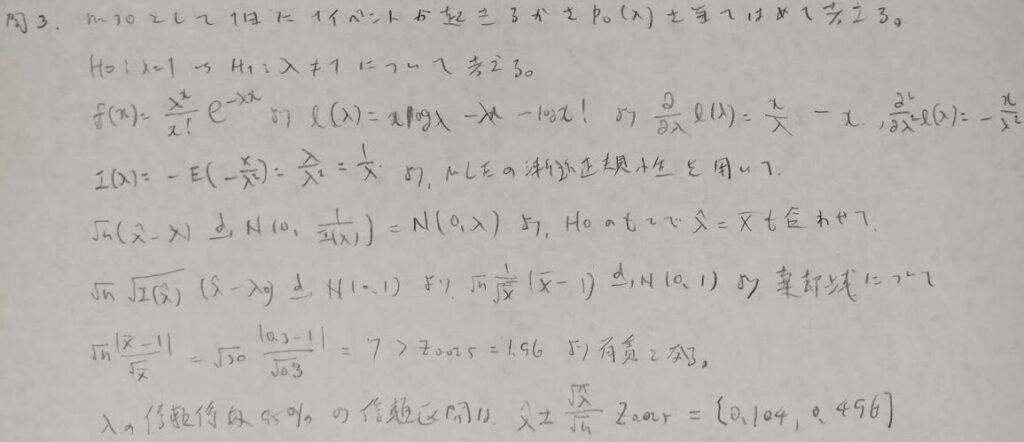
問4:2集団の母平均の検定
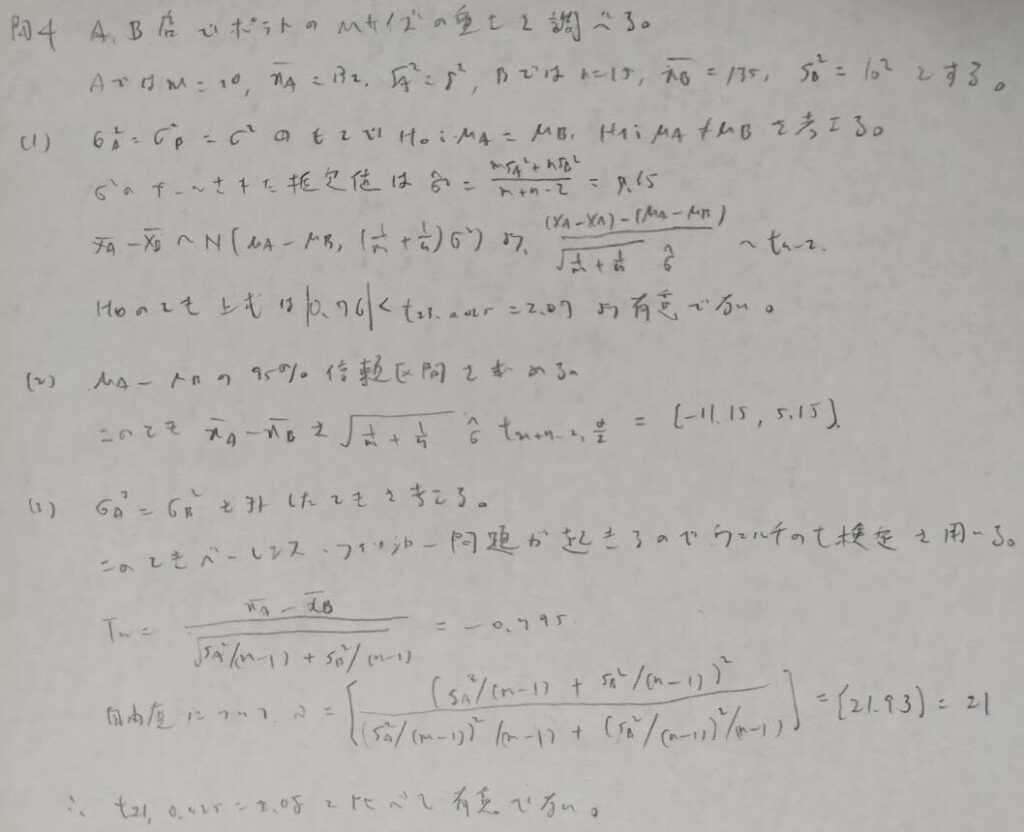
問5:ベルヌーイ母集団のサンプルサイズ
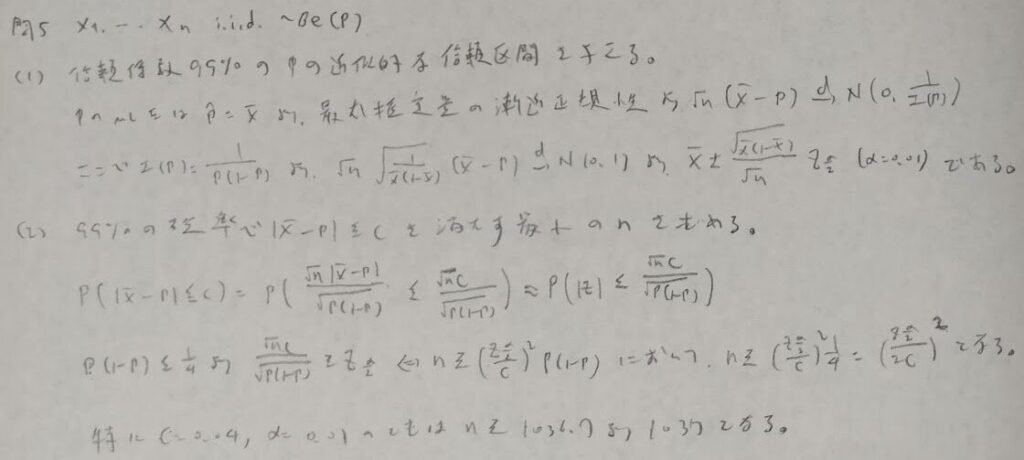
問6:多項分布の総合問題

問7:ポアソン母集団の総合問題

問8:2変数正規分布の1変数化

問9:P値
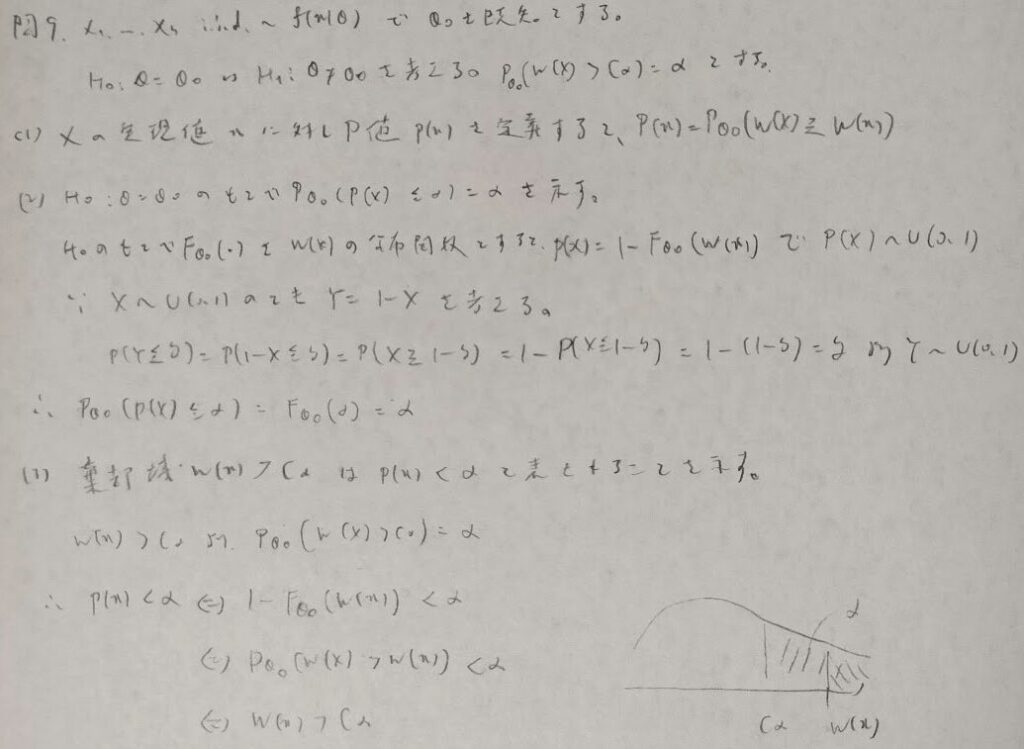
P値の問題は分布関数で考えると考えやすいです!
問10:正確な棄却域
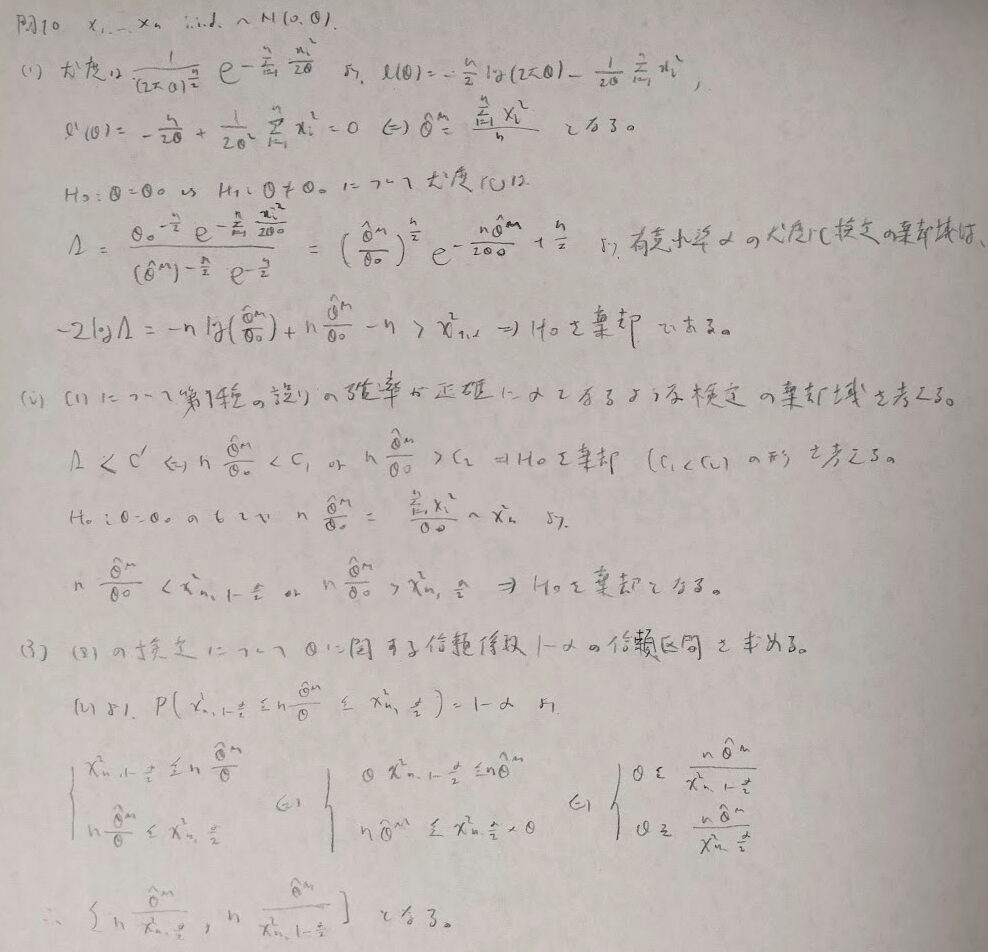
以上で青本『データ解析のための数理統計入門』の統計検定1級の統計数理に該当する章の解説が終了しました。次章からは統計応用の内容となります。







