アクチュアリー数学で必要な公式を過去問をベースに総整理しました。なお公式は『アクチュアリー試験 合格へのストラテジー 数学 第2版』を元にしております。本書はアクチュアリー数学受験のバイブルで受験者は必携の書です。
各章では分野ごとに最もベストな教材を紹介しております。
また本記事の後半は2025年の試験直前期時点での抑えておきたい重要な過去問を抜粋して紹介します。問題は1962年(昭和37年)から解いたデータを元にして、問題レベルとして簡単すぎず、また捨て問といわれる難問を除いて合否を分ける問題を抜粋し2025年のアクチュアリー数学の予想問題として掲載しました。
アクチュアリー数学:確率分野
3分野の中では暗記量の多さは中程度ですが、アクチュアリー数学ではt分布とF分布の確率密度関数、期待値や分散まで覚えていないと時間切れになります。
組み合わせの関連公式
まずは組み合わせ関連の公式を一気に解説します。
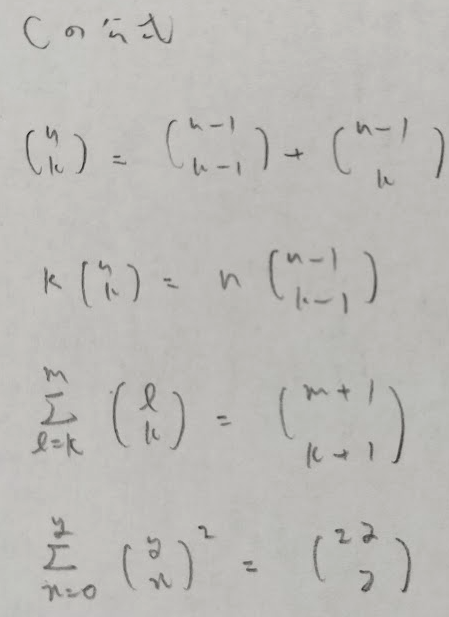
上の公式の大統領問題を一般化させると次のPとCのコンボの公式が導かれます。

次にホッケースティック恒等式を導出します。
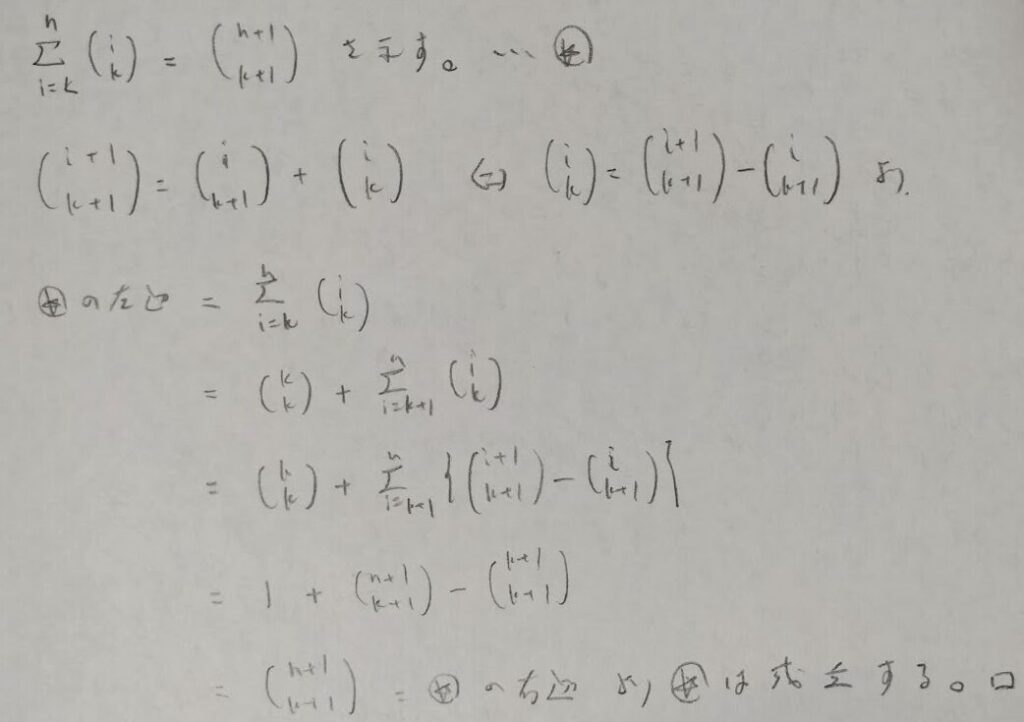
アクチュアリー数学の参考書に証明までは載っていませんでしたが追記しました。数式だと抽象的ですが、パスカルの三角形を持ち出すと単純なお話になり、外側のラインから対角線に下ろした数字(二項係数)を止まるまで全て足して、止まった箇所の右下が和に相当しているということです。
過去問を解く際に以下のヴァンデルモンドの恒等式も知っておくべきだと思い追記します。
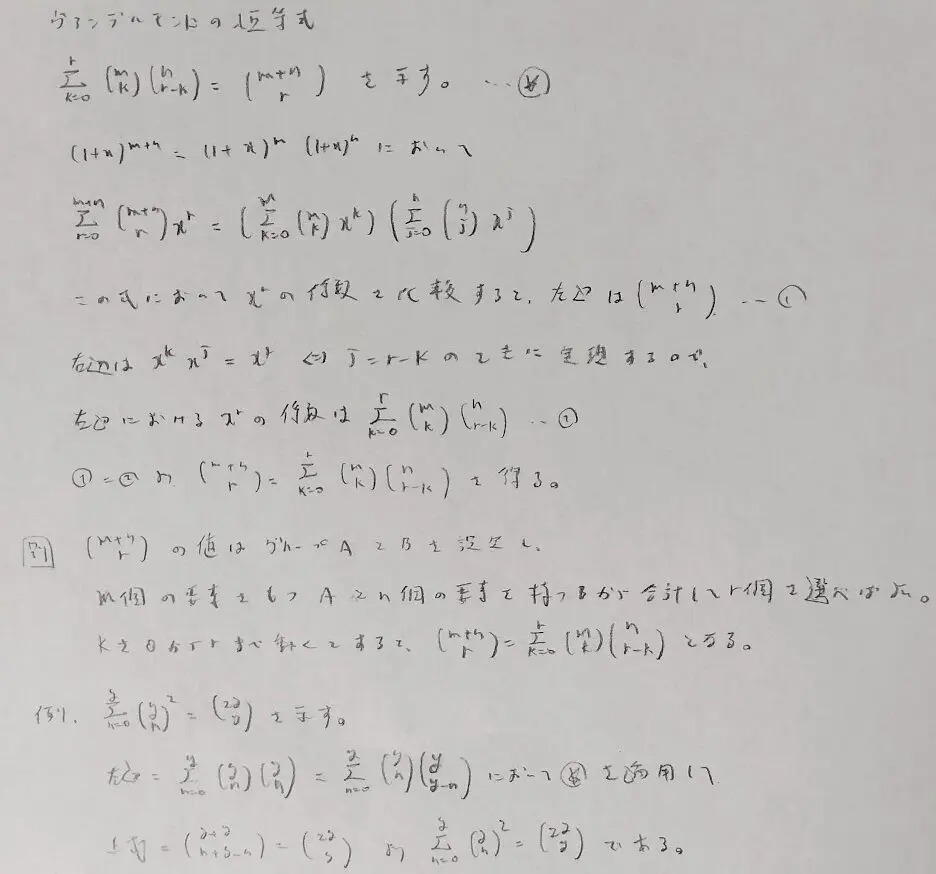
負の二項定理
次は負の二項定理で序盤の難所です。
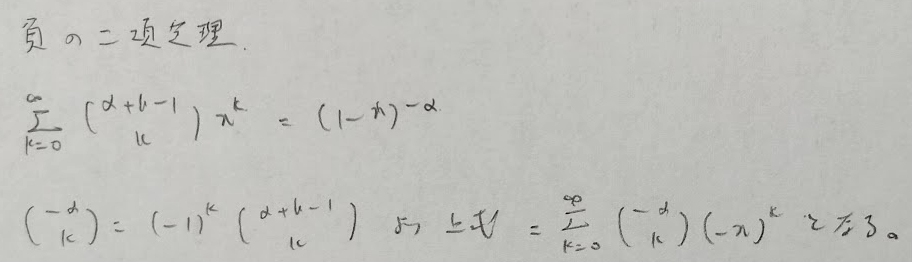
個人的に負の二項分布は覚えにくく体系立てて整理してみました。ご覧ください。

積分公式
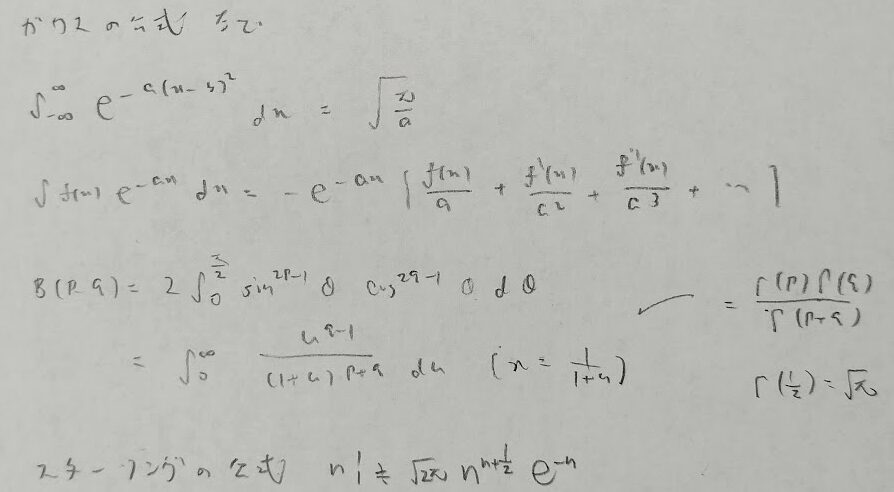
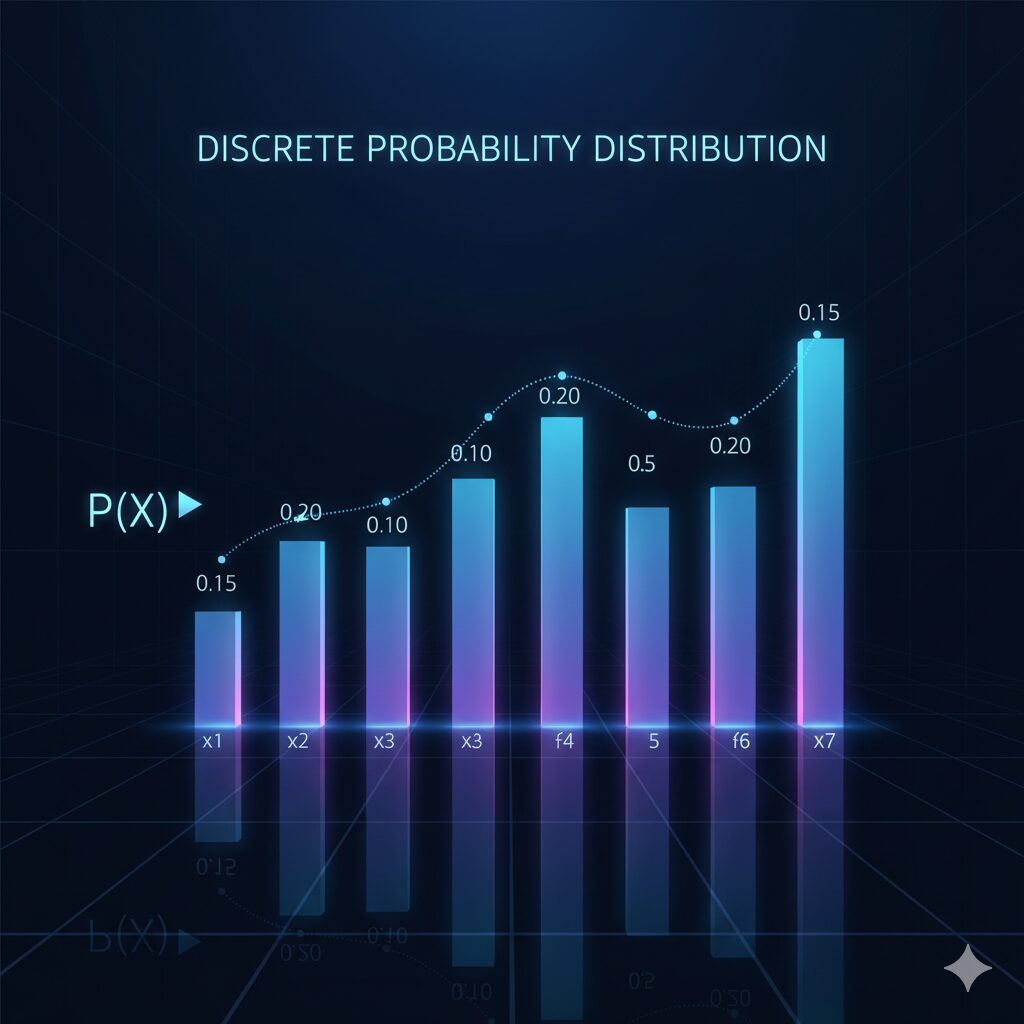
離散型確率分布
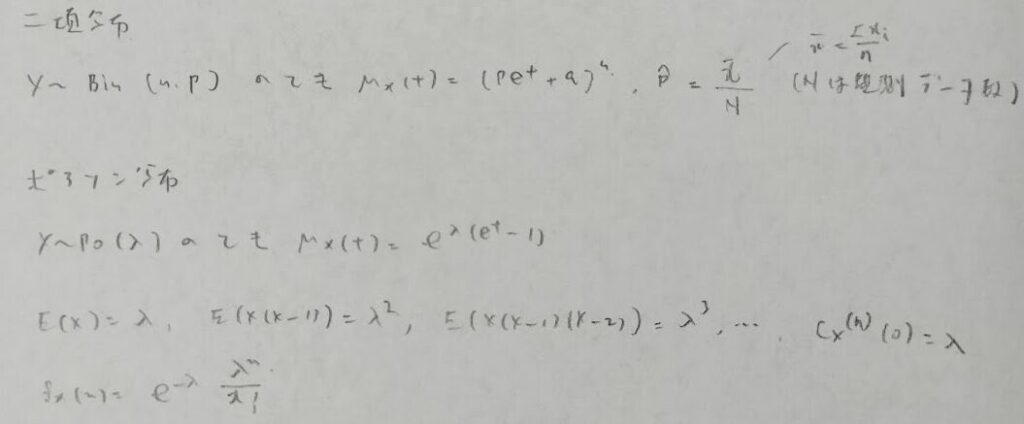
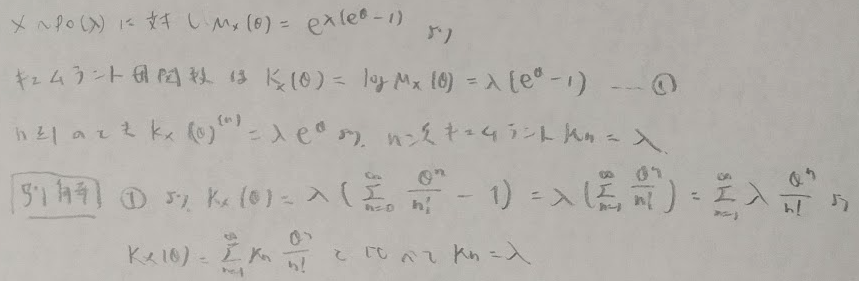
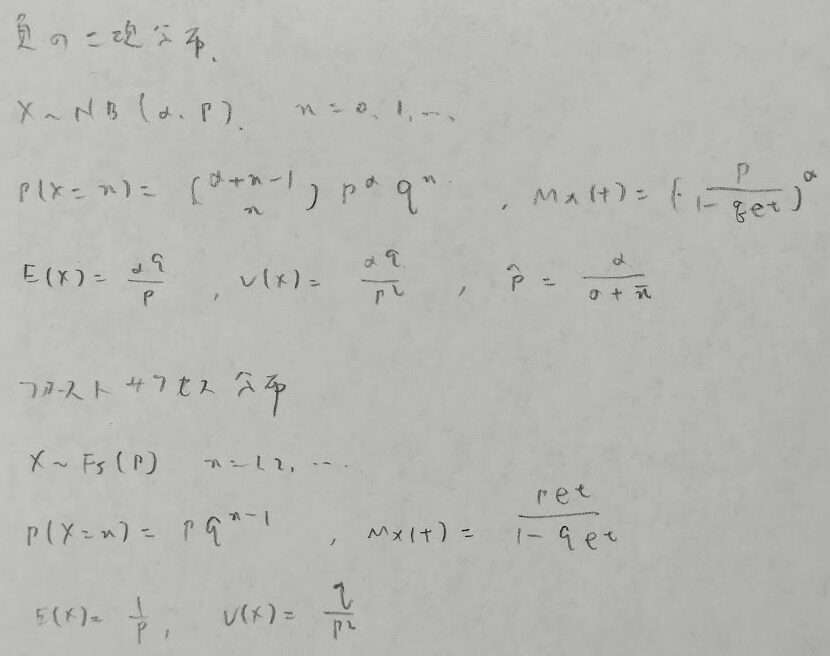
幾何分布の生存関数:P(X>x)は、失敗回数がx回を超える場合なので、初成功がx回後の失敗の後に起きる確率、つまり独立なx回の試行がすべて失敗する確率と考えればよいので、q^xとなります。ファーストサクセス分布の生存関数も結果の式は等しくなります。ファーストサクセス分布の生存関数は、x回試行しても初成功していないと考えます。
ファーストサクセス分布と離散一様分布はやや似ています。n個のものから当たりの1つを当てるまでの試行回数をk回とするとき、前者は復元抽出で、後者は非復元抽出で行うときの試行回数kが従う分布となります。負の二項分布のパラメータの推定値は感覚的に当たり前だと考えれば暗記量を減らせます。
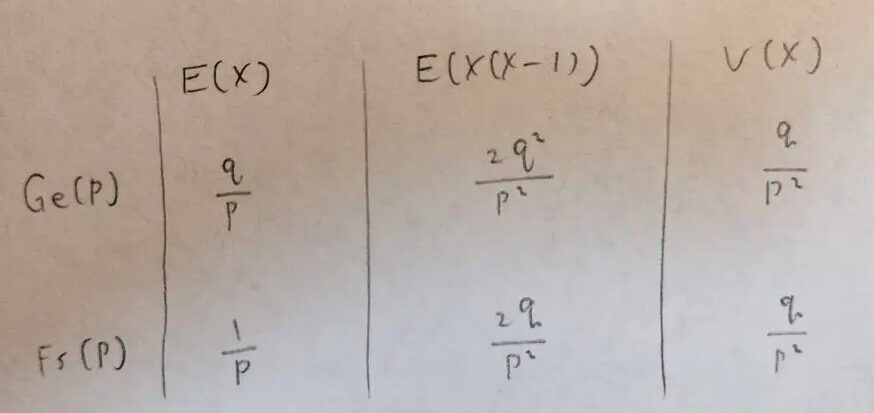
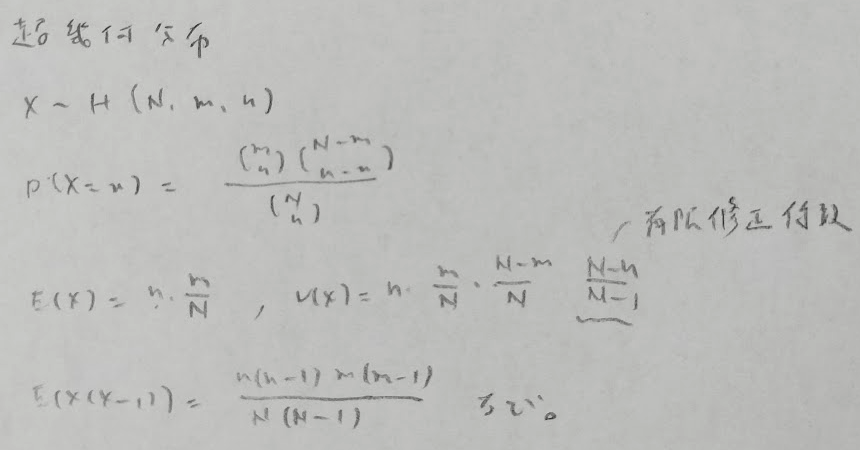

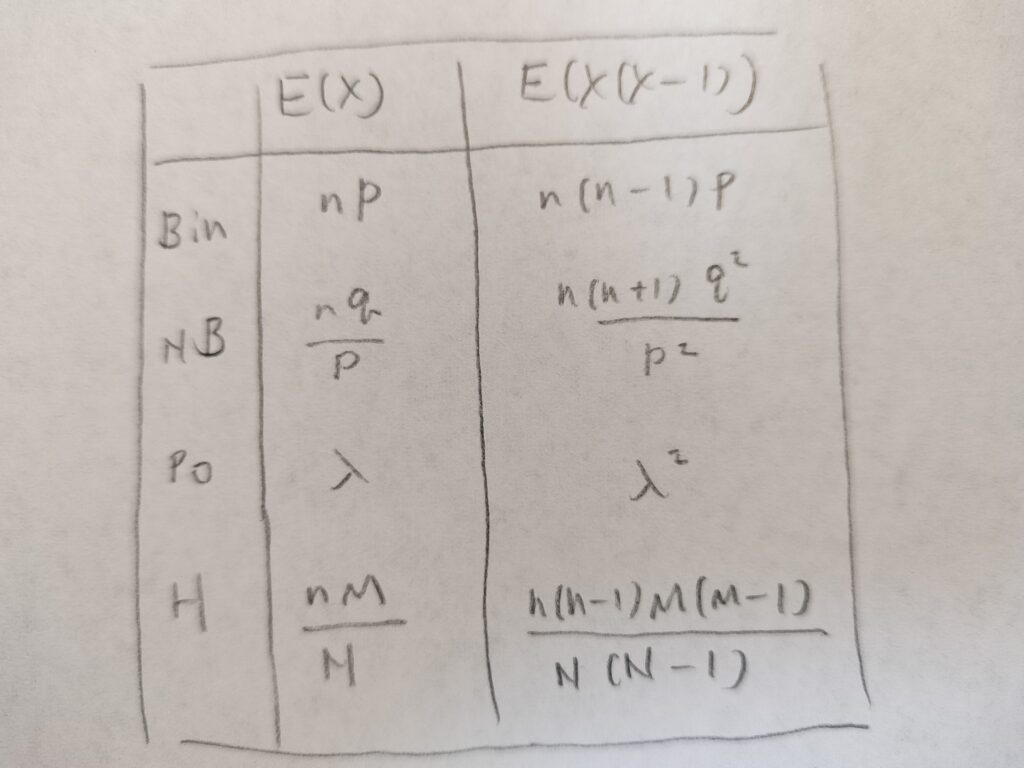
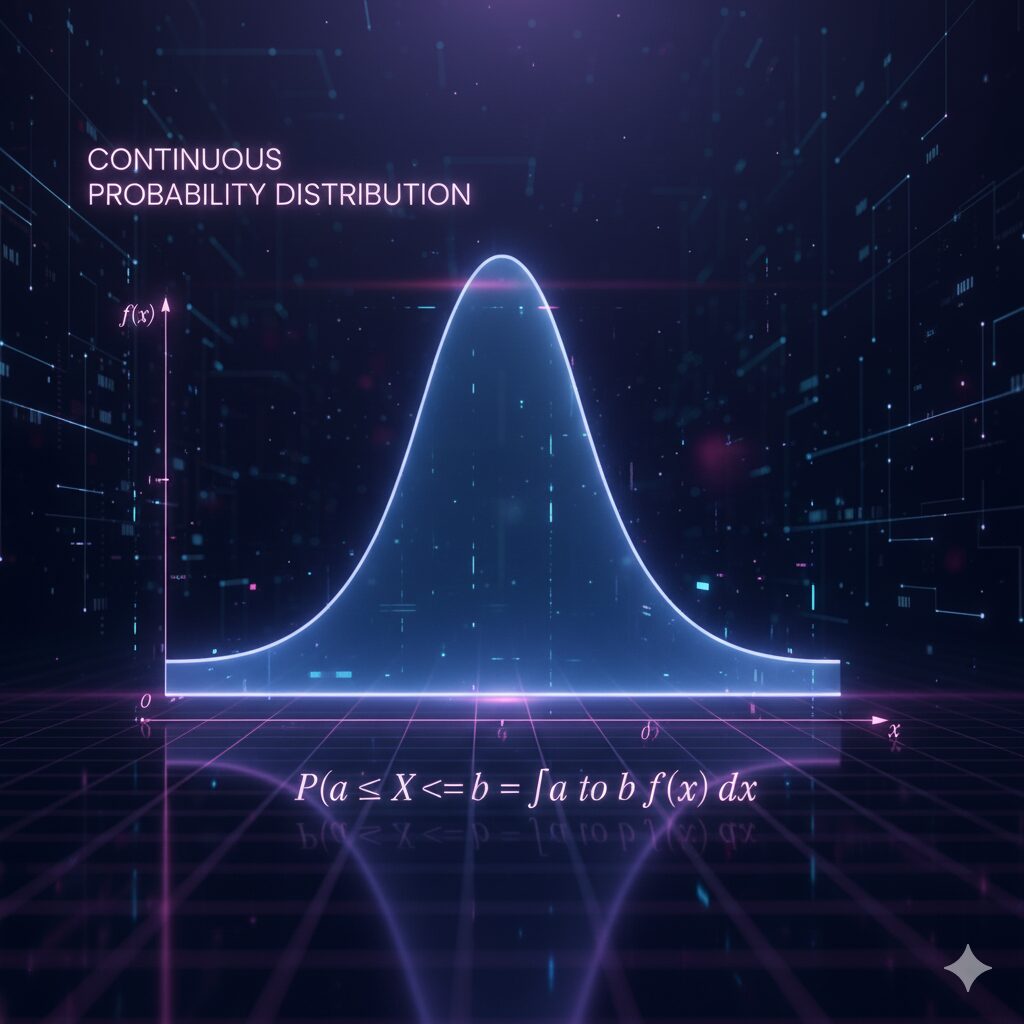
連続型確率分布
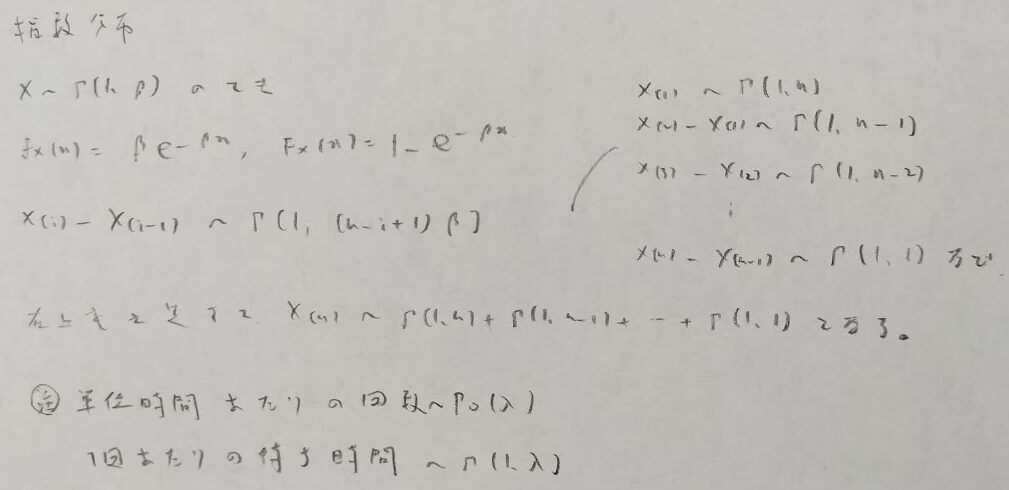
指数分布は生存関数の方を覚えた方が良いです。分布関数は1から生存関数を引けば良いからです。生存関数について、時間が経つにつれて生存確率は下がっていきます。それをe^-(故障率λ)(時間t)という極自然な式で表現しています。
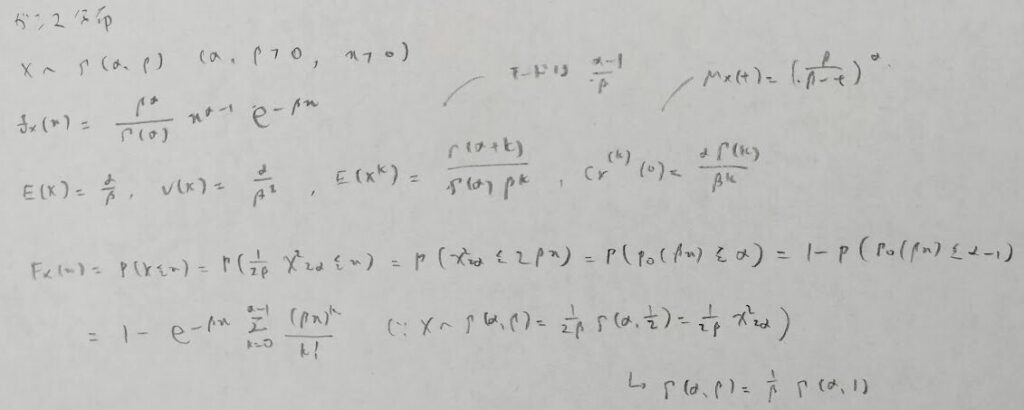
積率母関数はベタベータのαと覚えます。モードの式は期待値よりも位置が左側というイメージで覚えましょう。
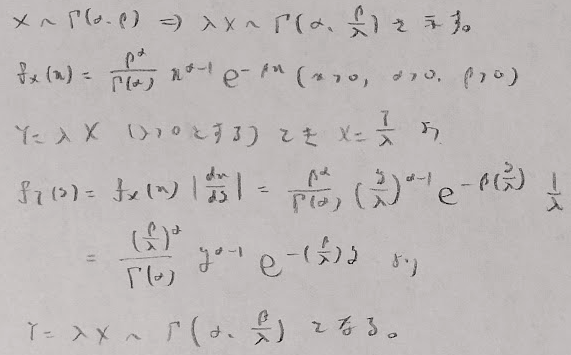
ガンマ分布のキュムラントの導出を行なっておきます。マクローリン展開がポイントです。
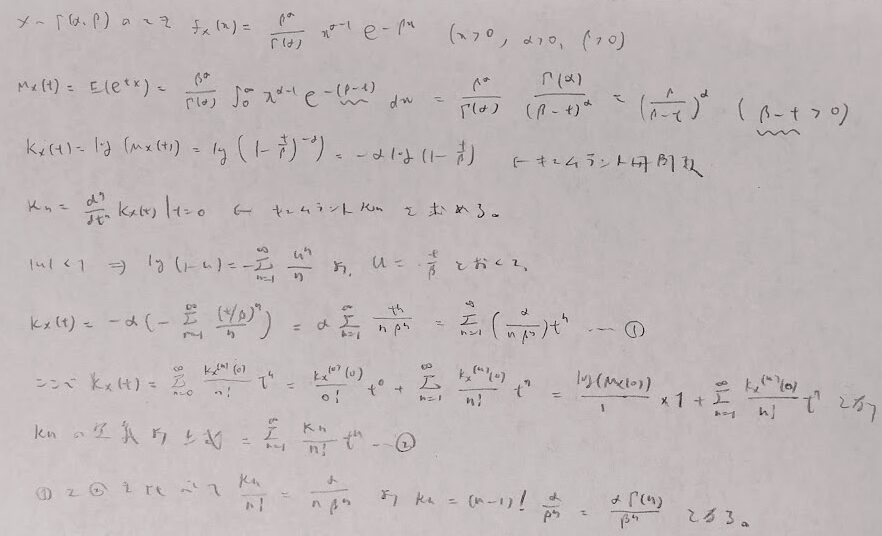
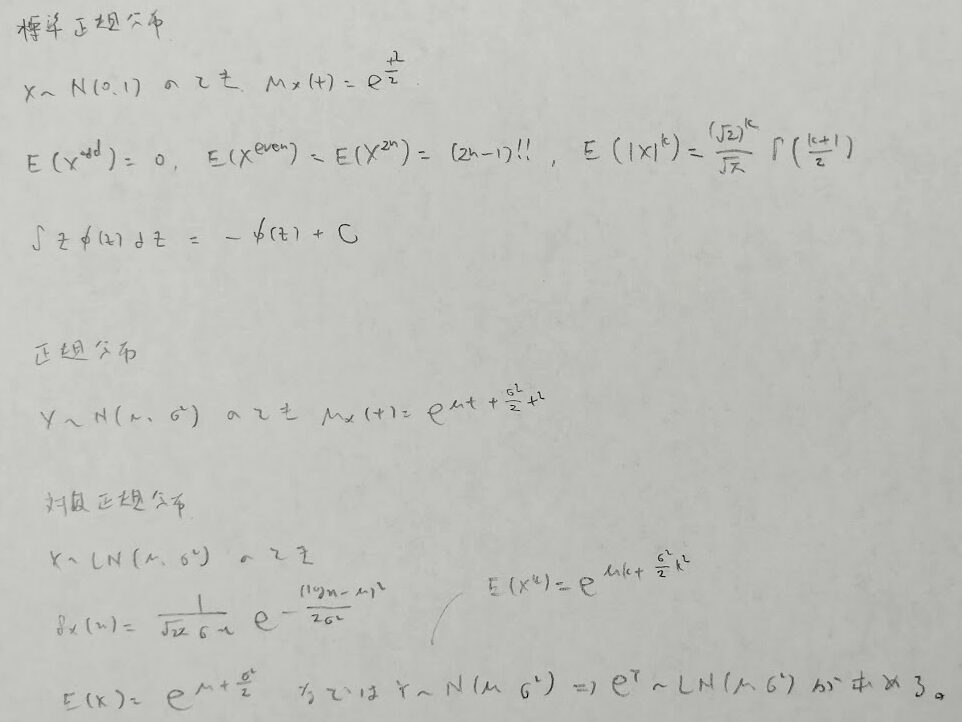
標準正規分布表を用いて偏差値について大体の数値がわかります。
X=50+10Z(Z~N(0,1))のとき偏差値Xがa以上の確率は順に、
65→7%,70→2%,75→0.6%,80→0.1%,90→0.003%,100→3・10^(-7)%です。
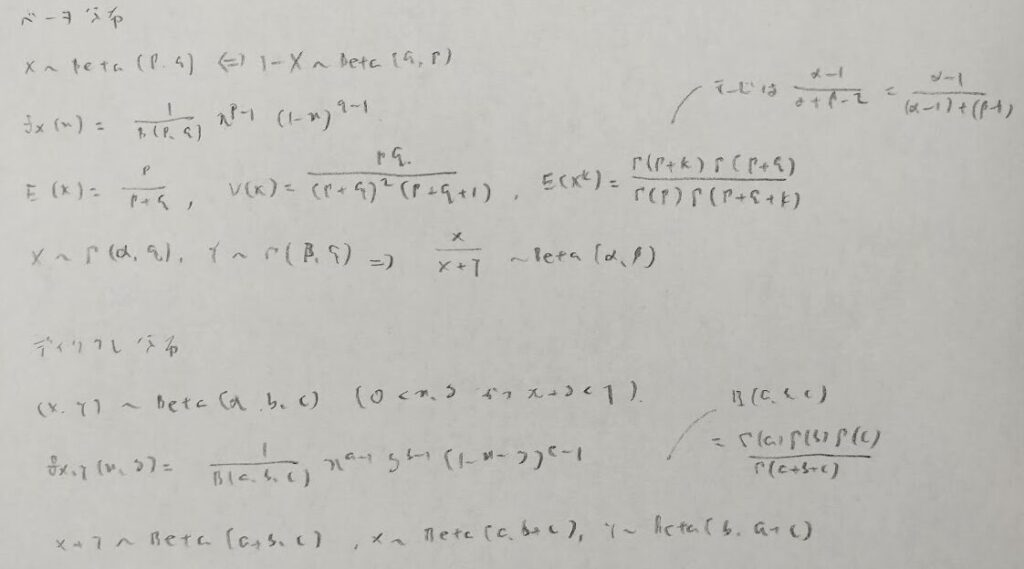
モードについては、ガンマ分布と似た感じで各々のパラメータから1を引いたものの期待値と覚えましょう。

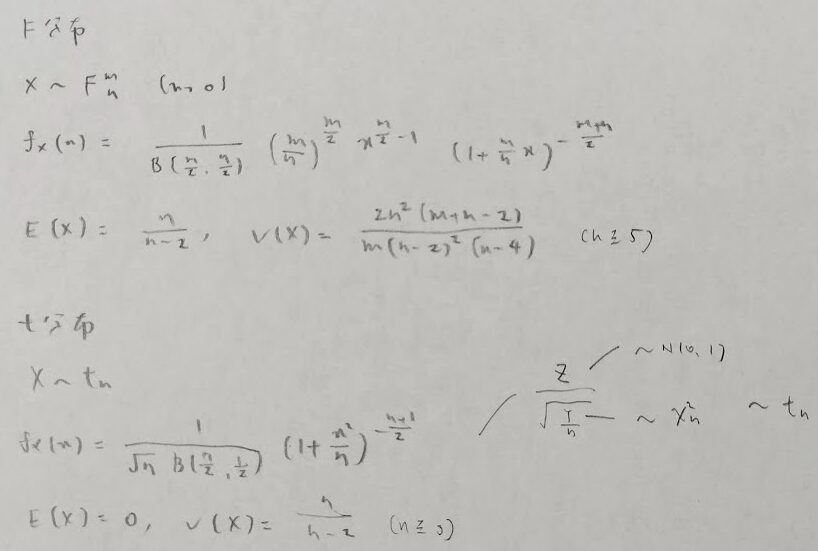
アクチュアリー数学では公式としてこれを覚えていないといけないのでF分布の分散の覚え方を教えます。というかGeminiさんがなかなかのインパクトのある覚え方を教えてくれました。

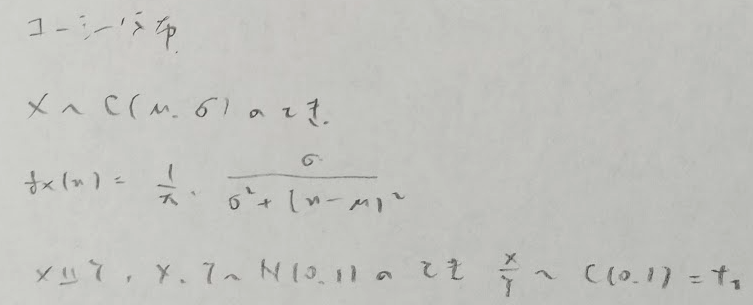
コーシー分布では期待値が存在しないため中心極限定理の利用はできませんが、2つのパラメータに関して再生性は持ちます。さらに特異的な性質として標準コーシー分布の独立なn個の標本における標本平均も標準コーシー分布に従います。

また標準コーシー分布の絶対値を利用してバーゼル問題を解くことができます。
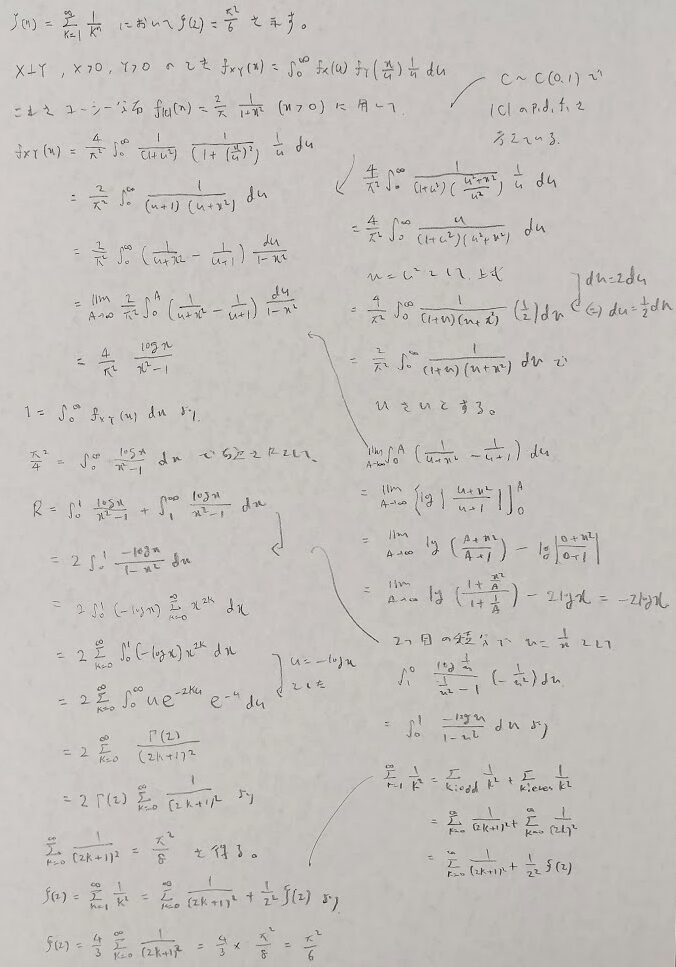
またコーシー分布はルーレット問題とも関わりがあります。
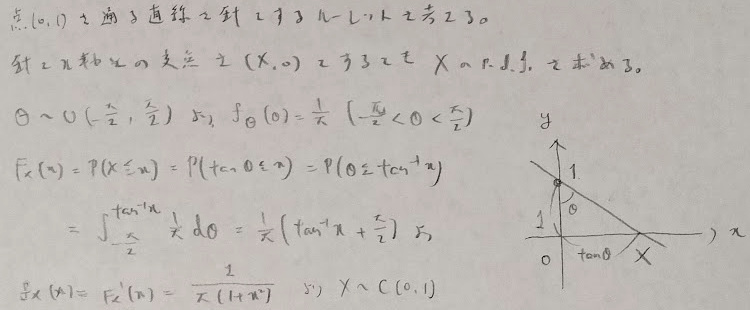
次はベータ分布関連です。
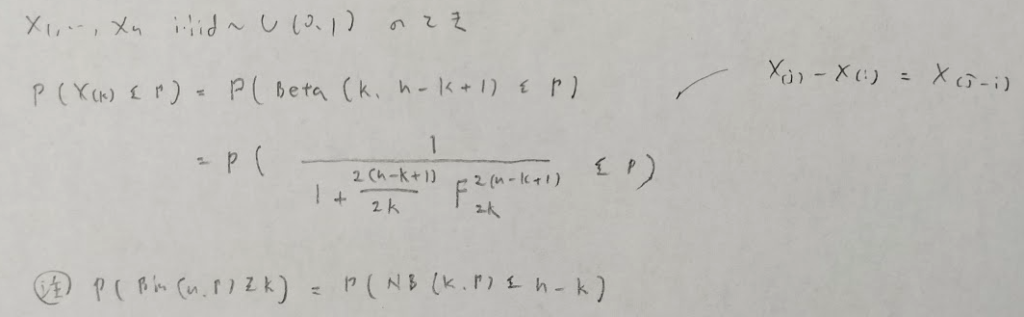
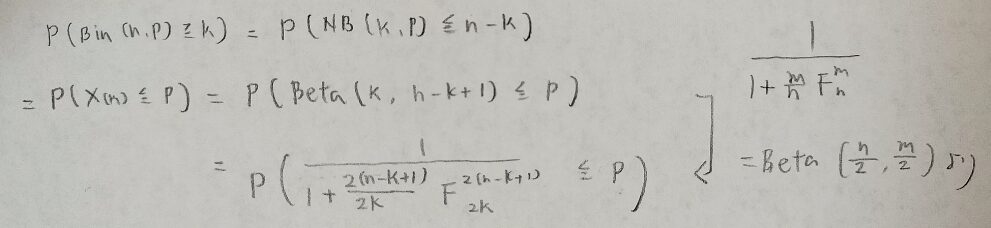
負の二項分布のところの語呂はケチャップエヌッケで覚えました。
しっぽ定理と高次モーメント
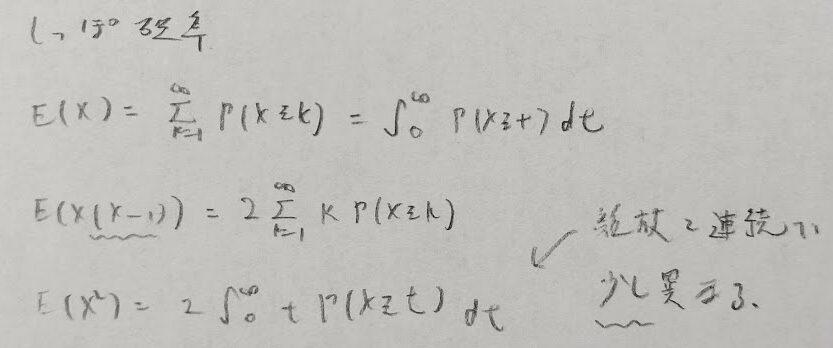
テイル確率には一般化が存在します。近年の難化するアクチュアリー数学の対策として一般形を覚えておくべきだと考えました。おそらく連続型の方が頻出です。

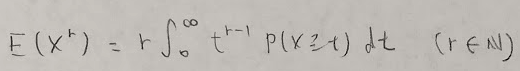
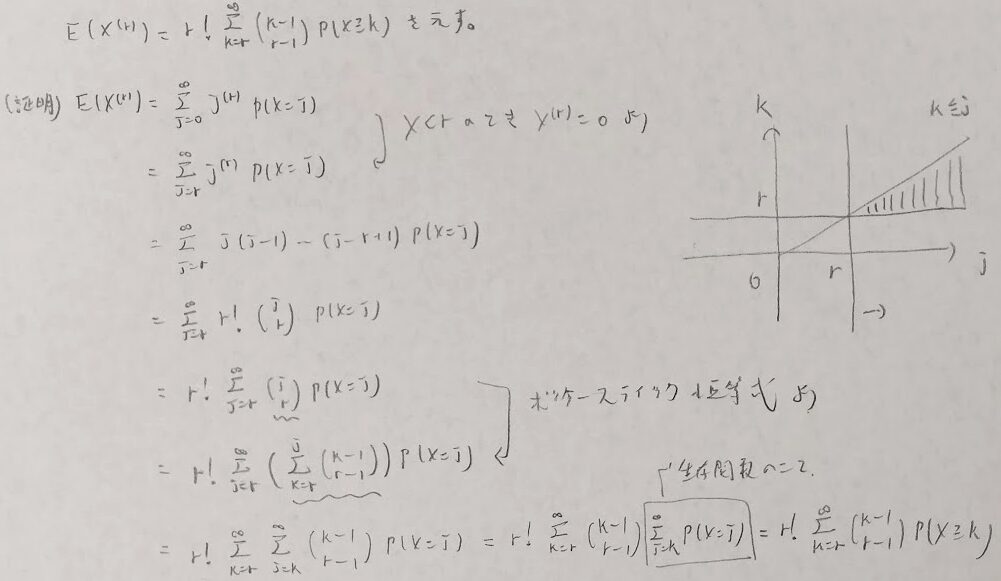

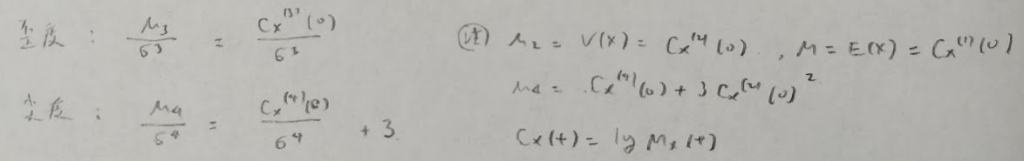
4次のキュムラントは4、3、2、2の順で数字が登場します。
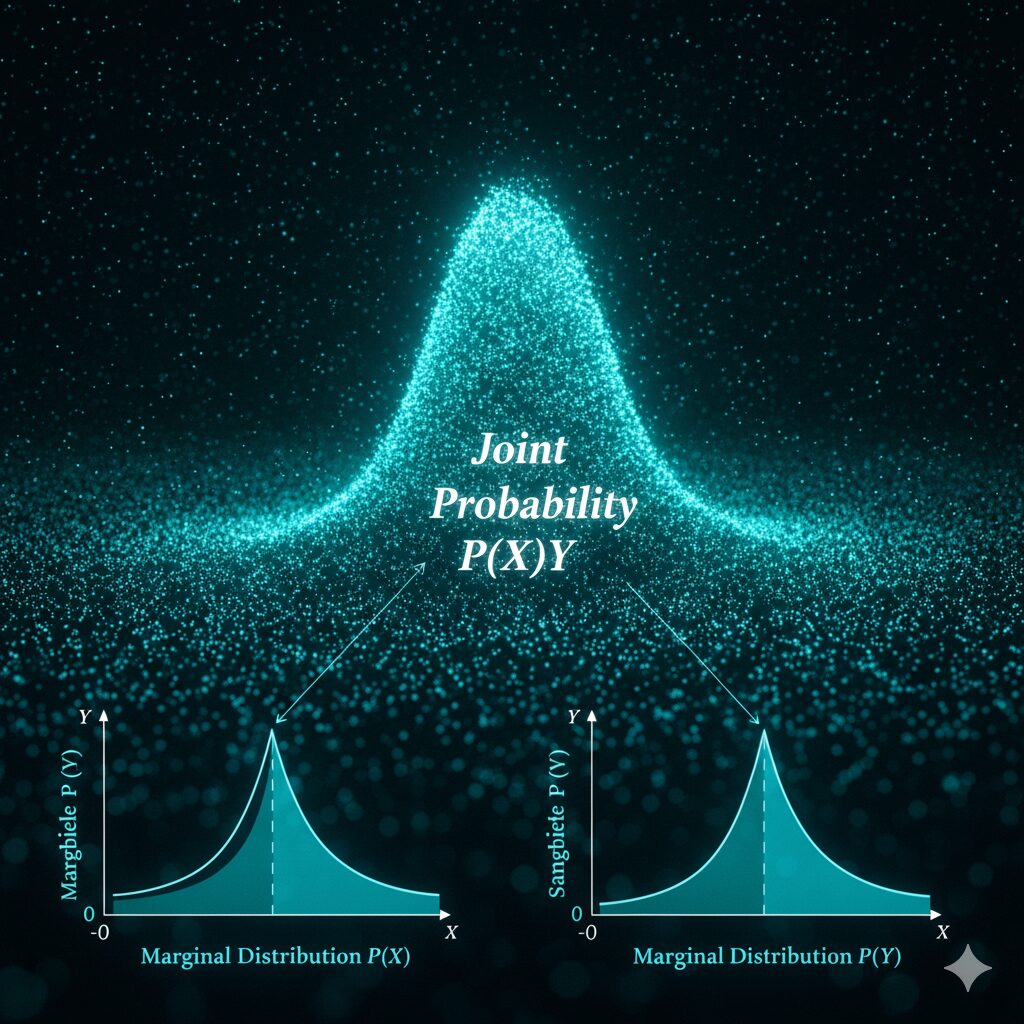
条件付き確率と多項分布
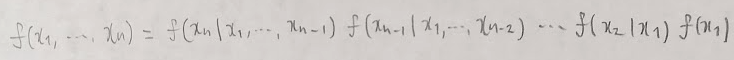

3つの性質の証明は次のようになります。

全期待値の公式は上で証明済みなので、全分散公式を証明しておきます。
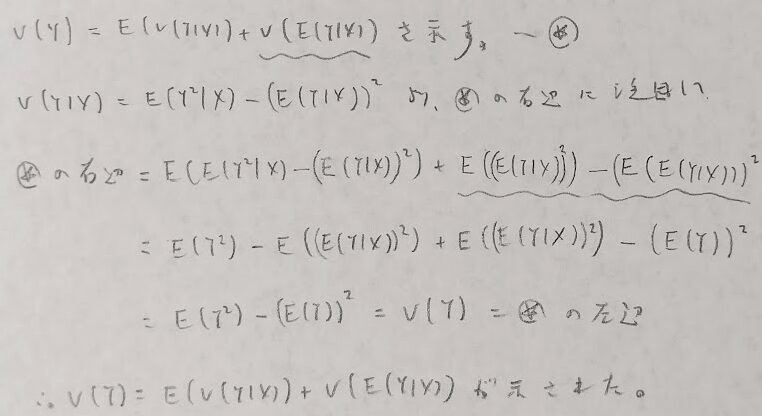
次に上の3つの例を証明します。最後の負の二項分布の問題は結論ありきの証明のため難易度が高いのです。
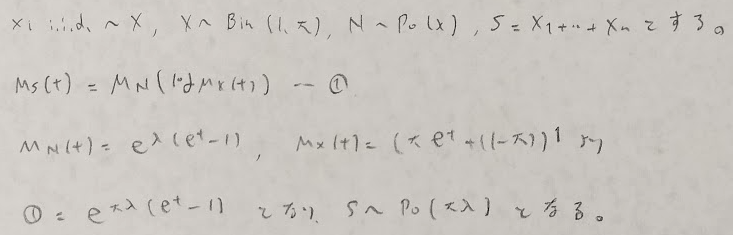


多項分布関連の公式の証明を載せます。
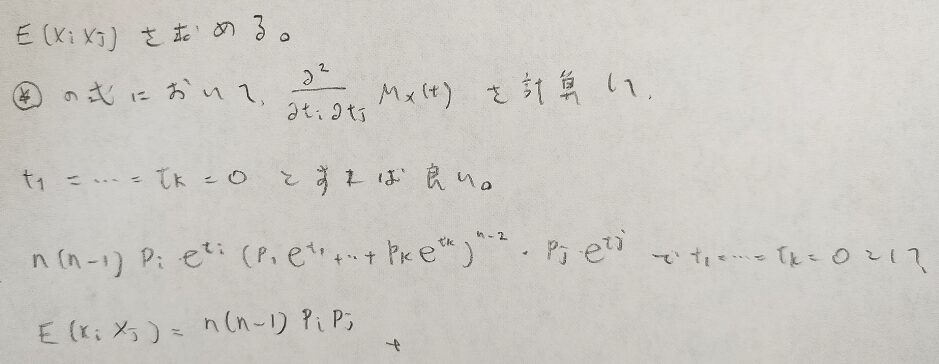
二項分布の期待値の式と似ています。共分散ではないのでマイナスはつきません。
確率の有名問題
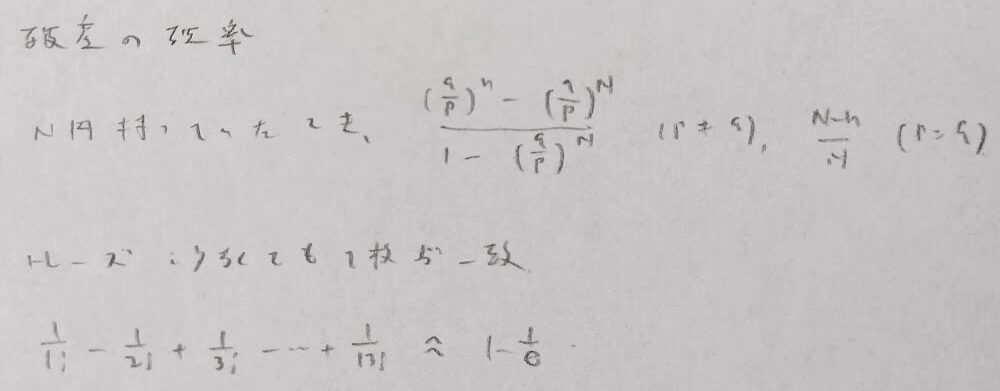
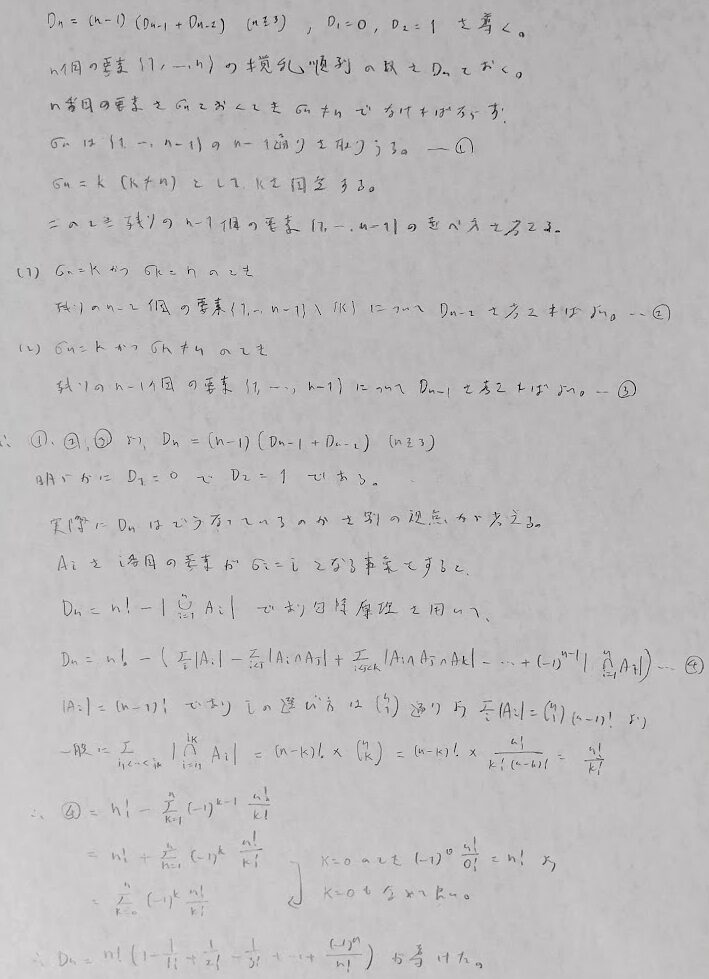
ポーカーの問題の解き方もまとめておきます。
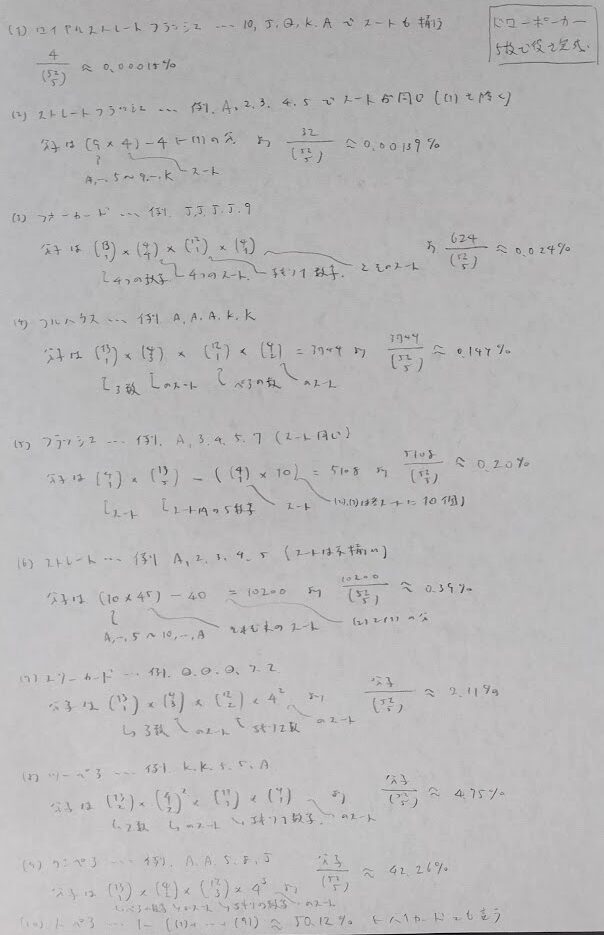
さらに次の一様分布に関係のあるBuffonの針の問題にも要注目です。
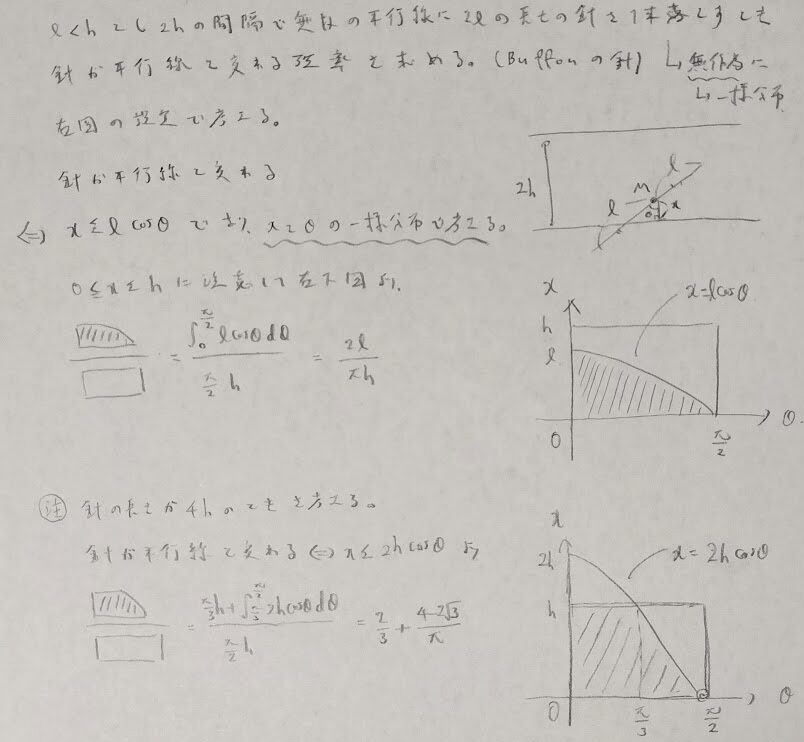
一様分布
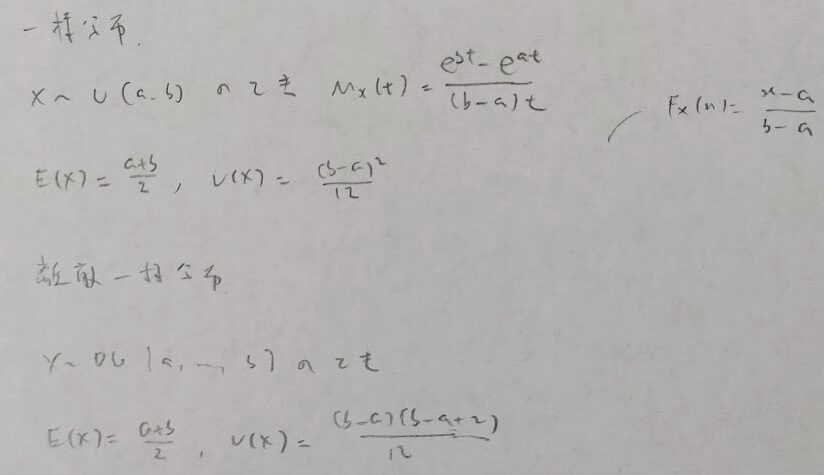
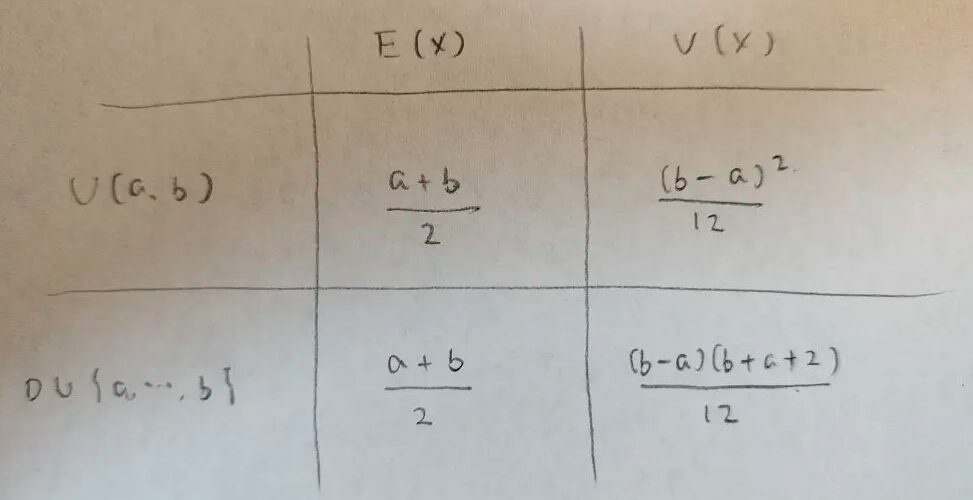
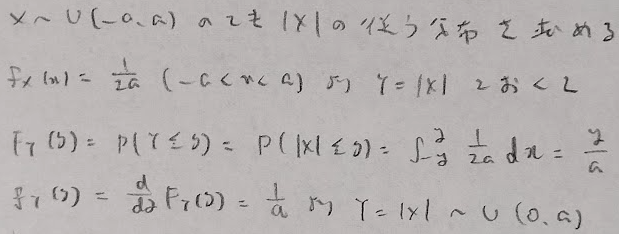
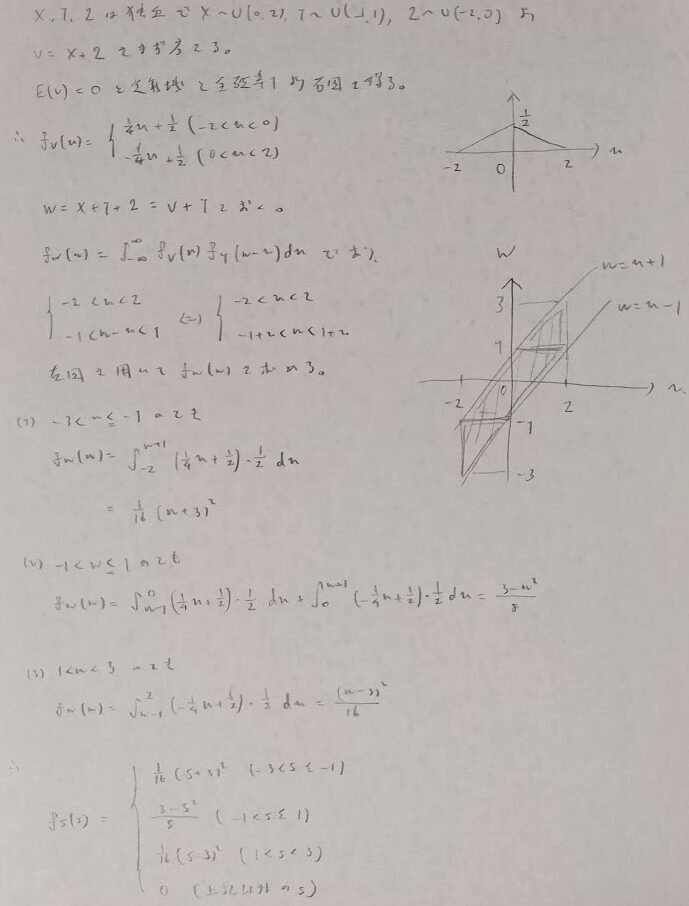
変数変換
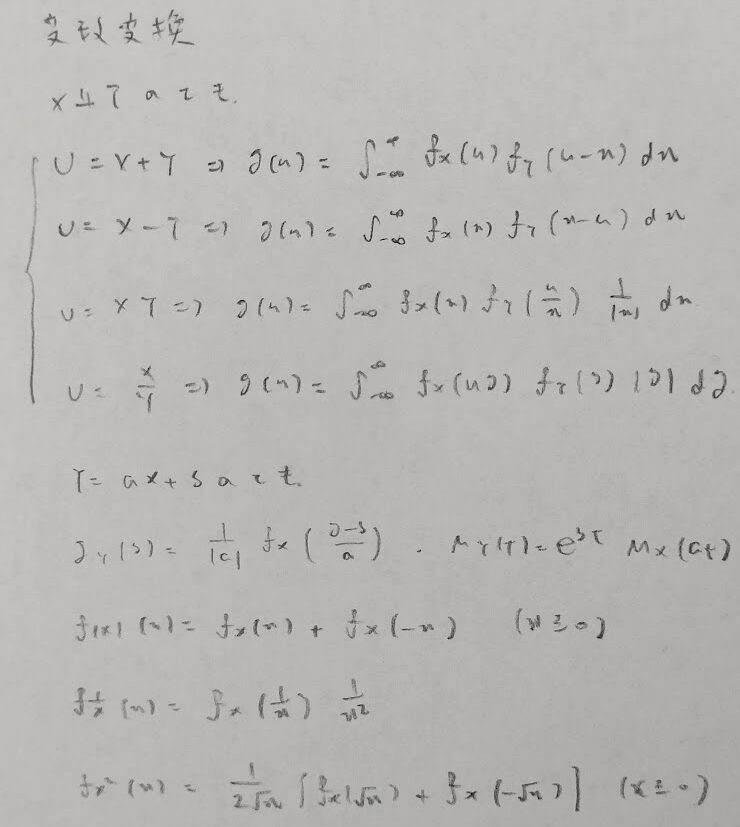
ただし一様分布系の問題は次のように考えるとスムーズになる場合が多いです。
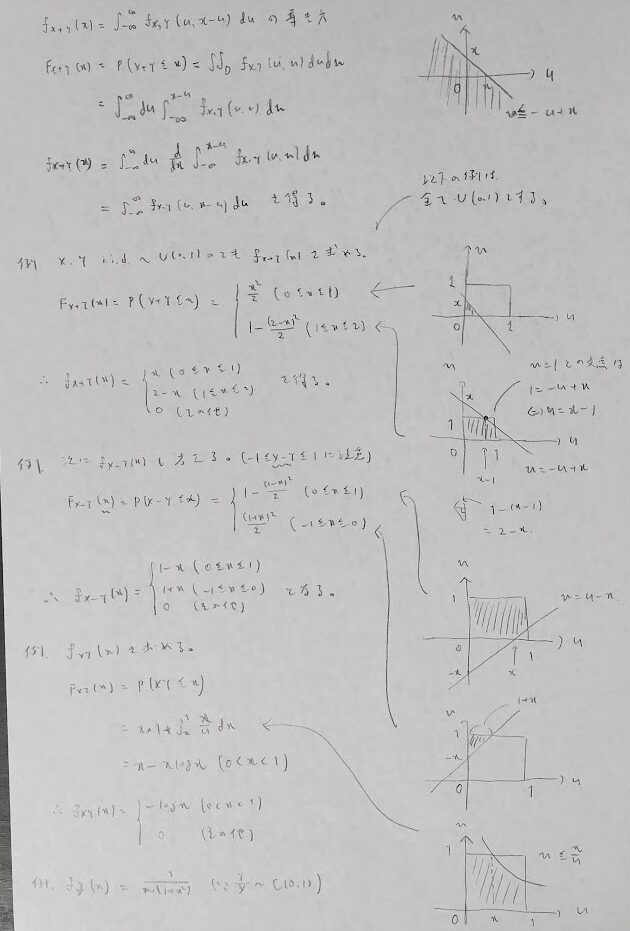
中心極限定理と多変量正規分布
誤差の問題は、中央値から幅の半分を両端に持つ一様分布を考えます。
多変量正規分布について頻出度は低いですが念のためまとめます。
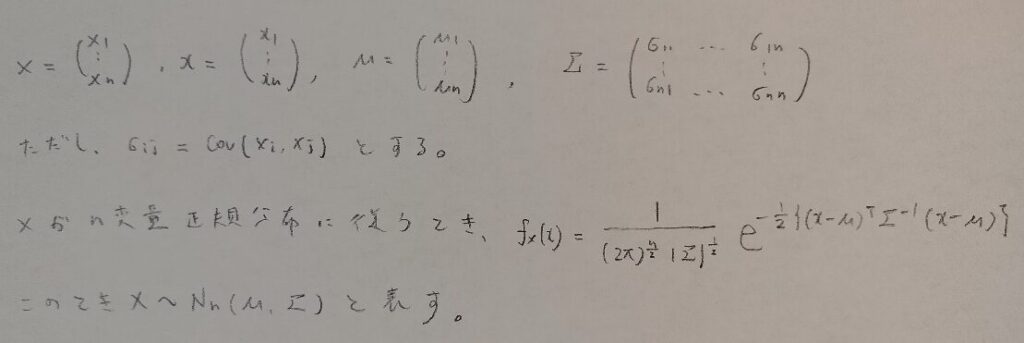
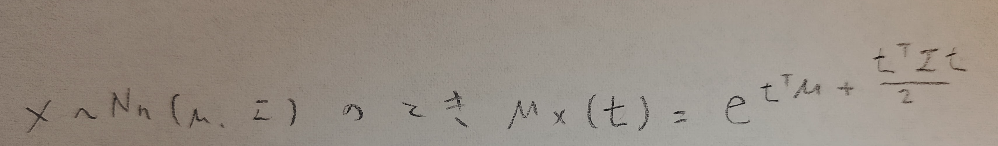
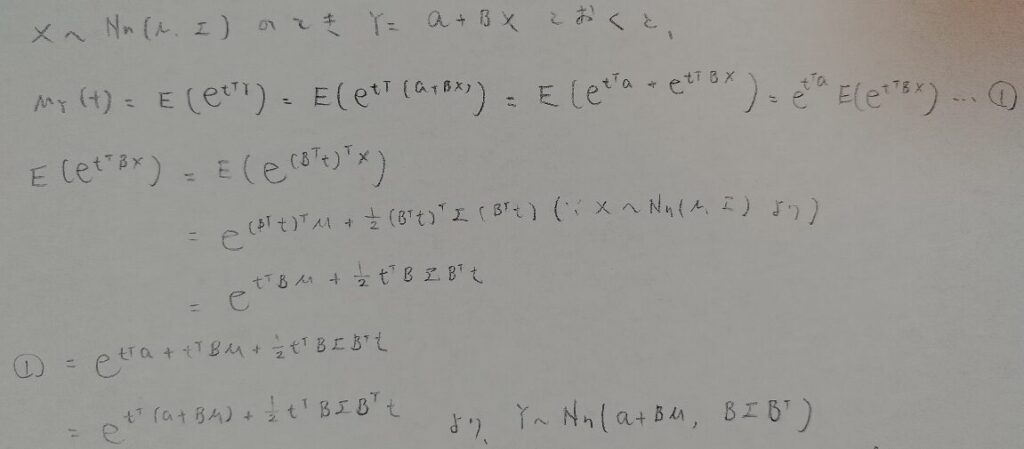
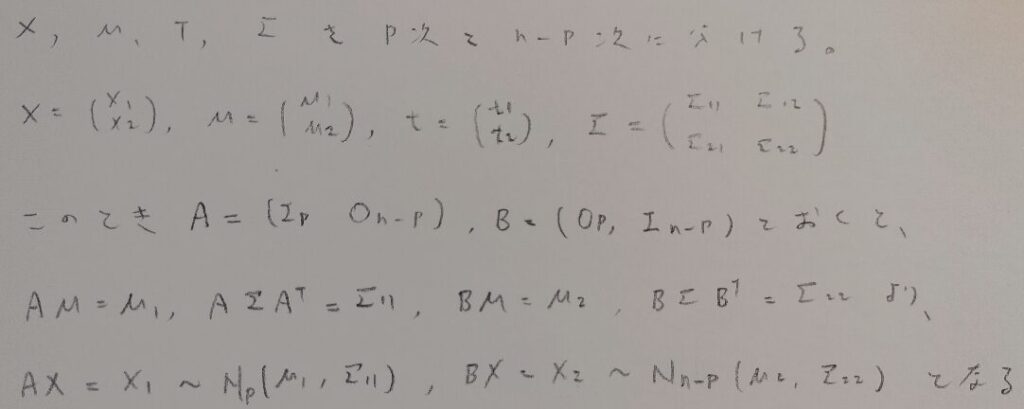
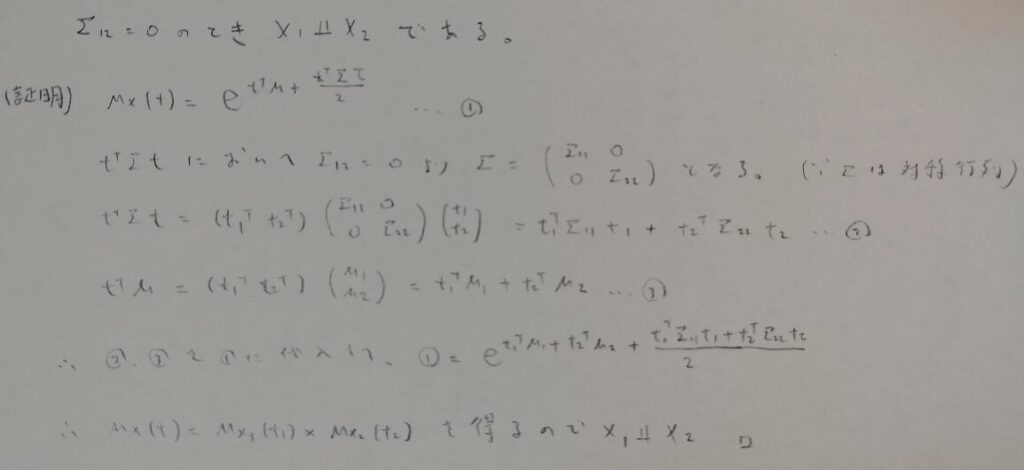
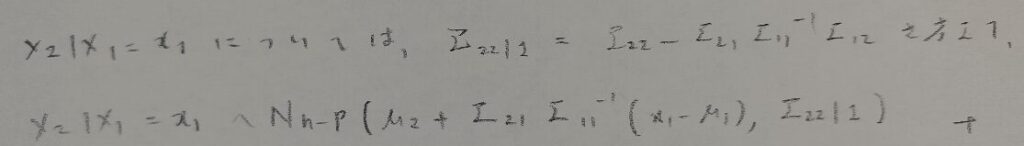
アクチュアリー数学:統計分野
二項母集団の精密法だけ別格です。そこだけ気をつければ暗記量はさほど多くはありません。
順序統計量とベータ分布

範囲の分布はベータ分布に帰着できるパターン以外は、暗記せず導出法を理解した方が良いと感じます。

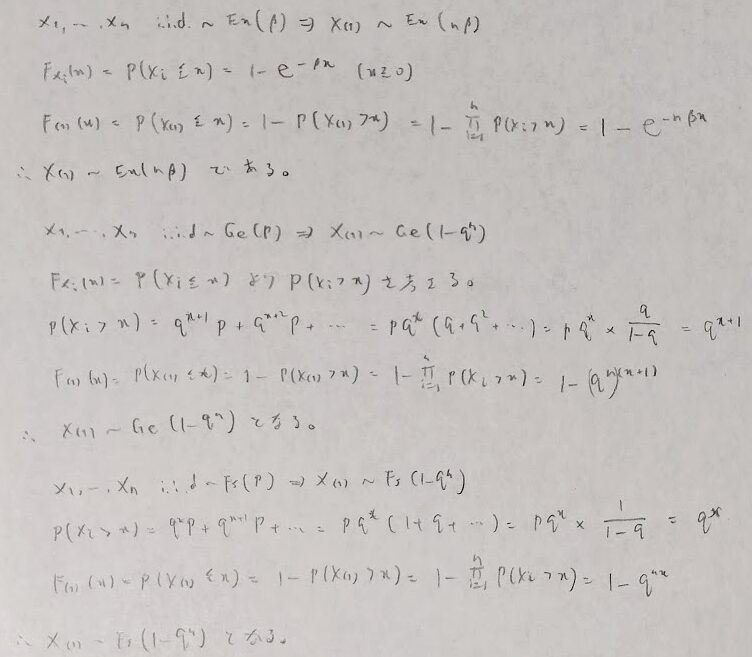
上の公式において指数分布の箇所を隣り合うを考えたものは次になります。
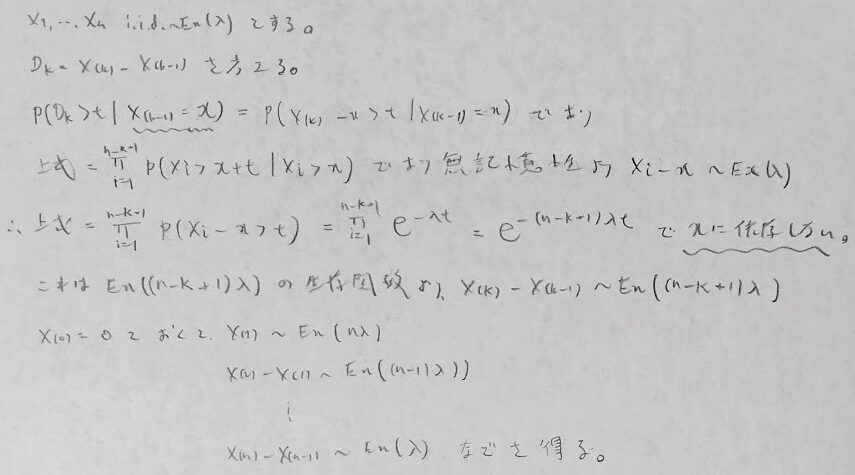
最大統計量関連では指数分布について次のような定理があります。
n個の独立で同一の指数分布に従う確率変数について、X_1+(X_2)/2+…+(X_n)/nはX_(n)と同じ分布に従います。
最後に順序統計量の分布関数に関する内容も含めた定義に従った証明を載せます。
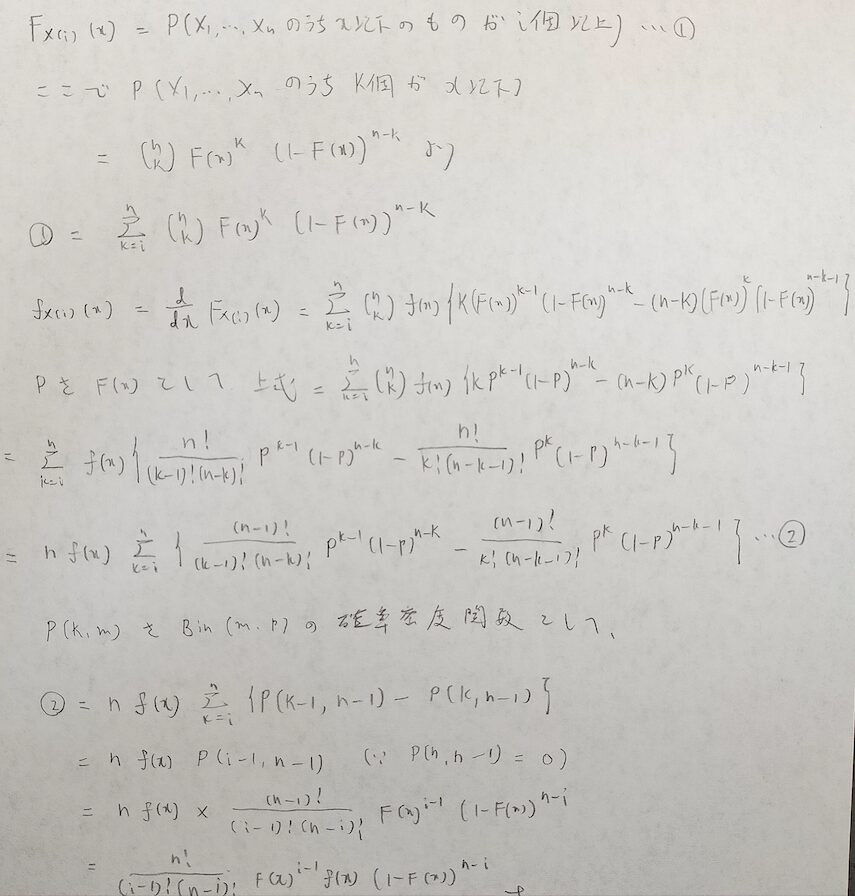
点推定
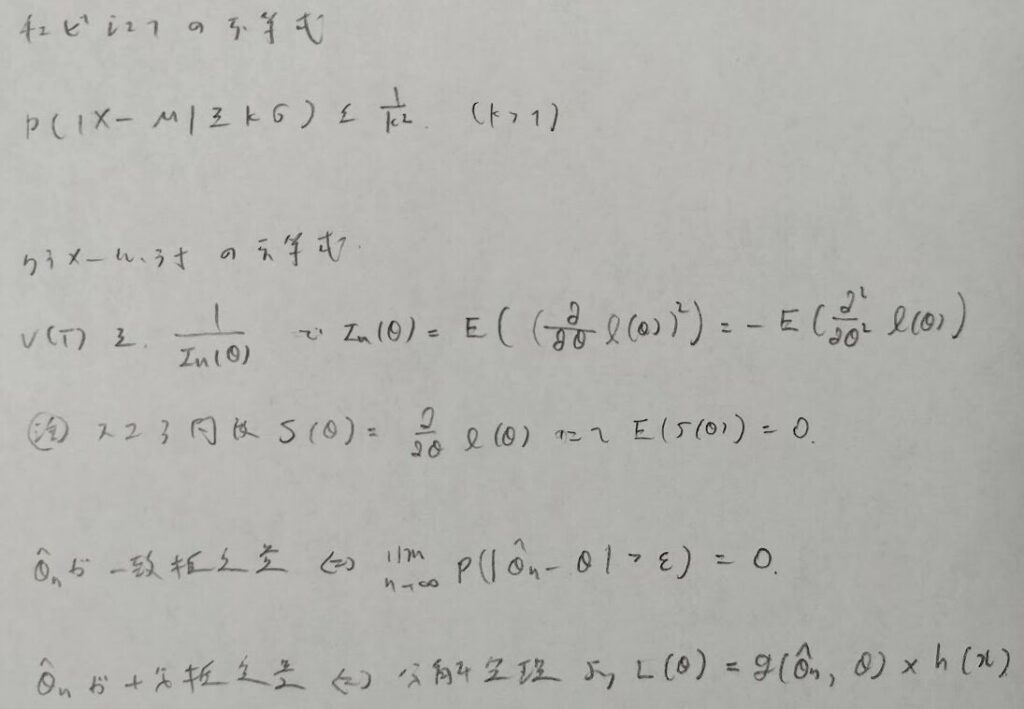
イェンセンの不等式は下記になります。この不等式は純粋数学でも多用されます。例えば確率関数をP(X=k)=1/n(k=1,…,n)とおき、g(x)=-log(x)とおきイェンセンの不等式を適用するとn変数の相加相乗不等式が得られます。

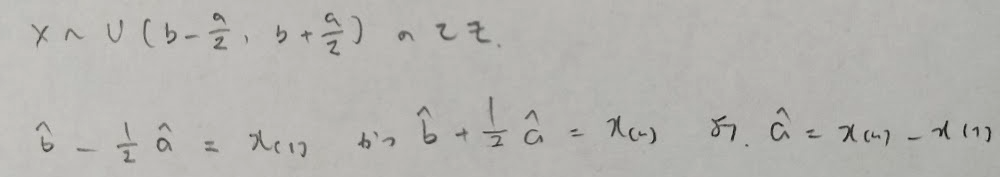
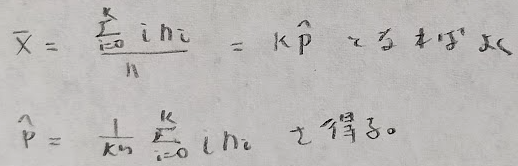
有効推定量を考える際は前提条件として不偏性を満たさなければなりません。
区間推定
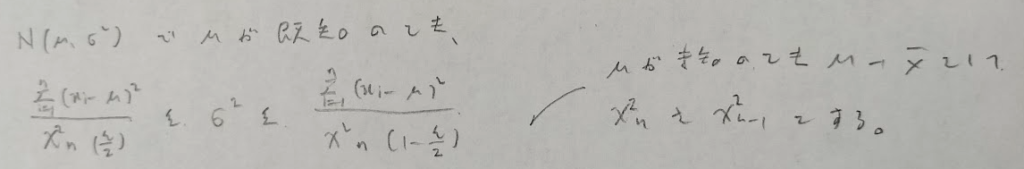
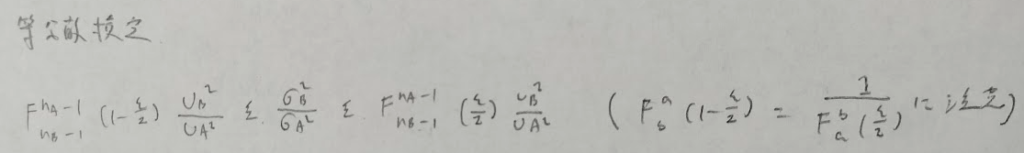
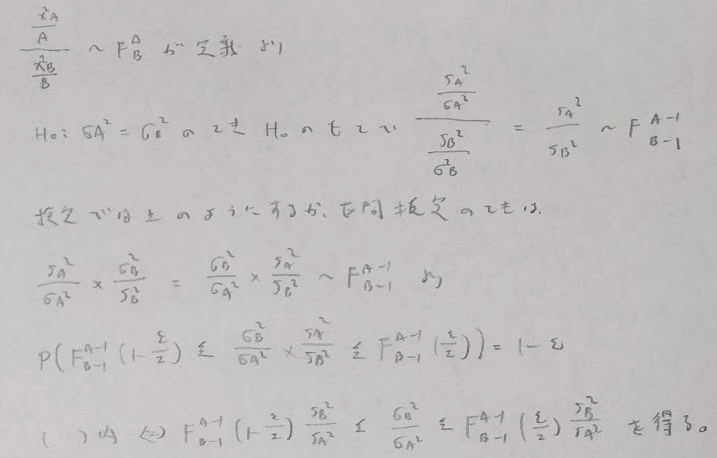
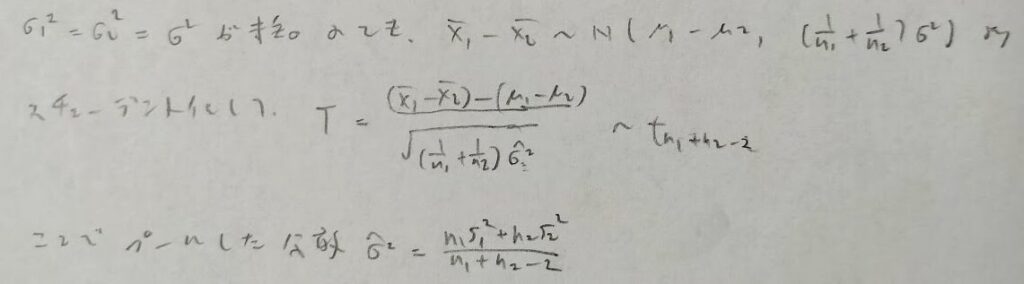
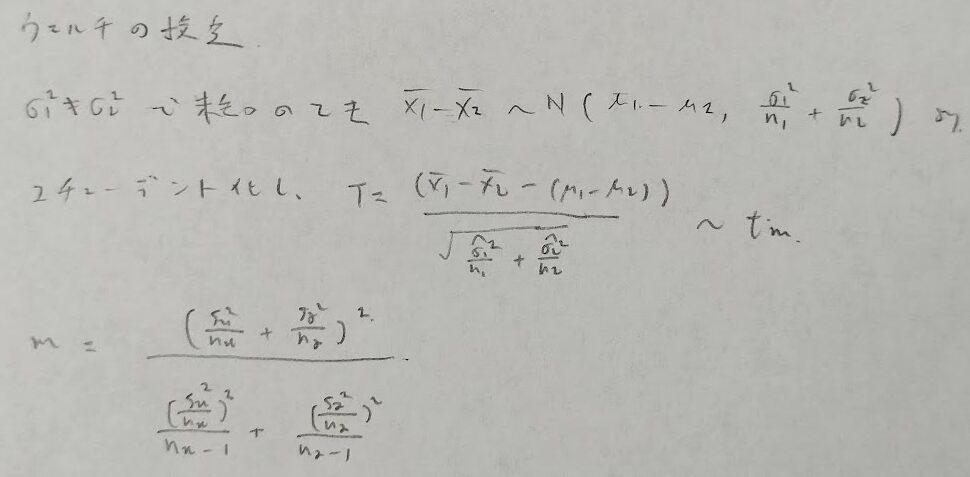
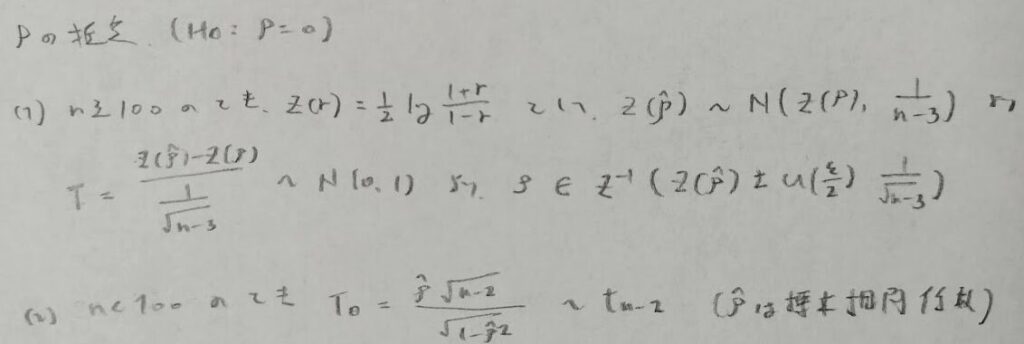
小標本の場合は分母分子ともに2がきます。また分子の方が頭でっかちです。つまり2因子あります。
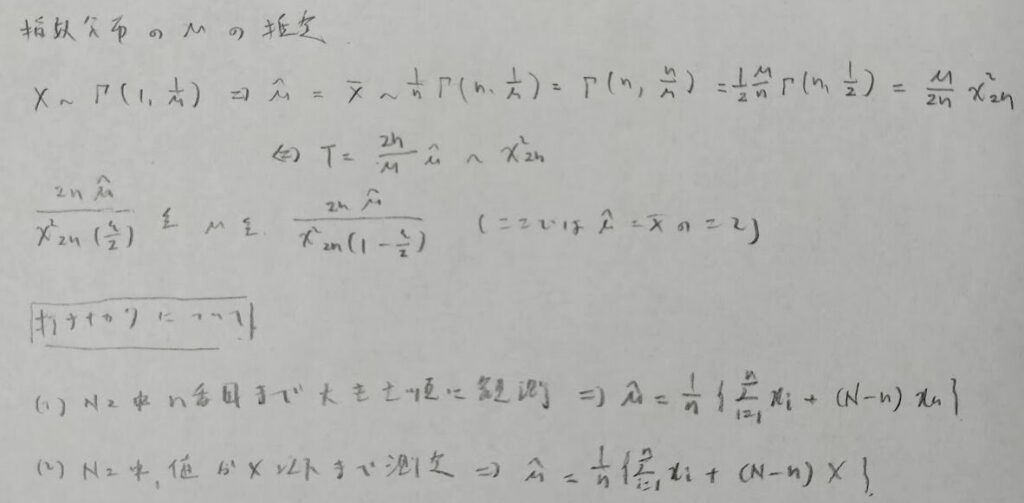
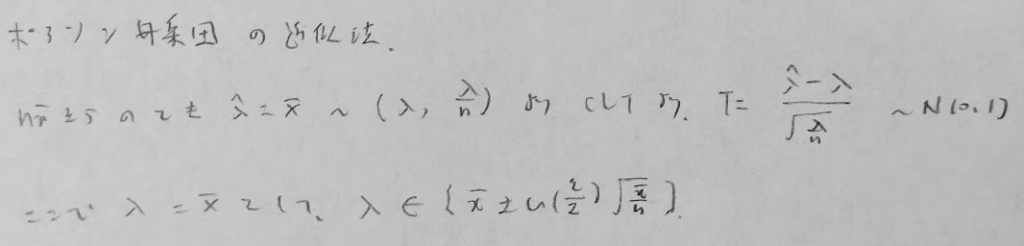
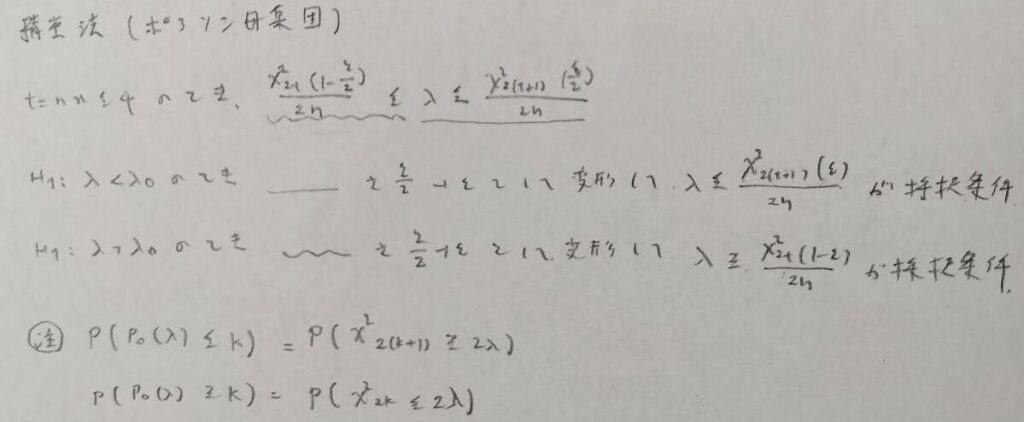
信頼区間の分子について、カイ2乗分布は自由度が大きくなればグラフは右にずれ込みます。そのため信頼区間は気持ち広めになっています。

信頼区間の左側の分子のインデックスは2です。注の()の中のnのインデックスはFの自由度とクロスしています。
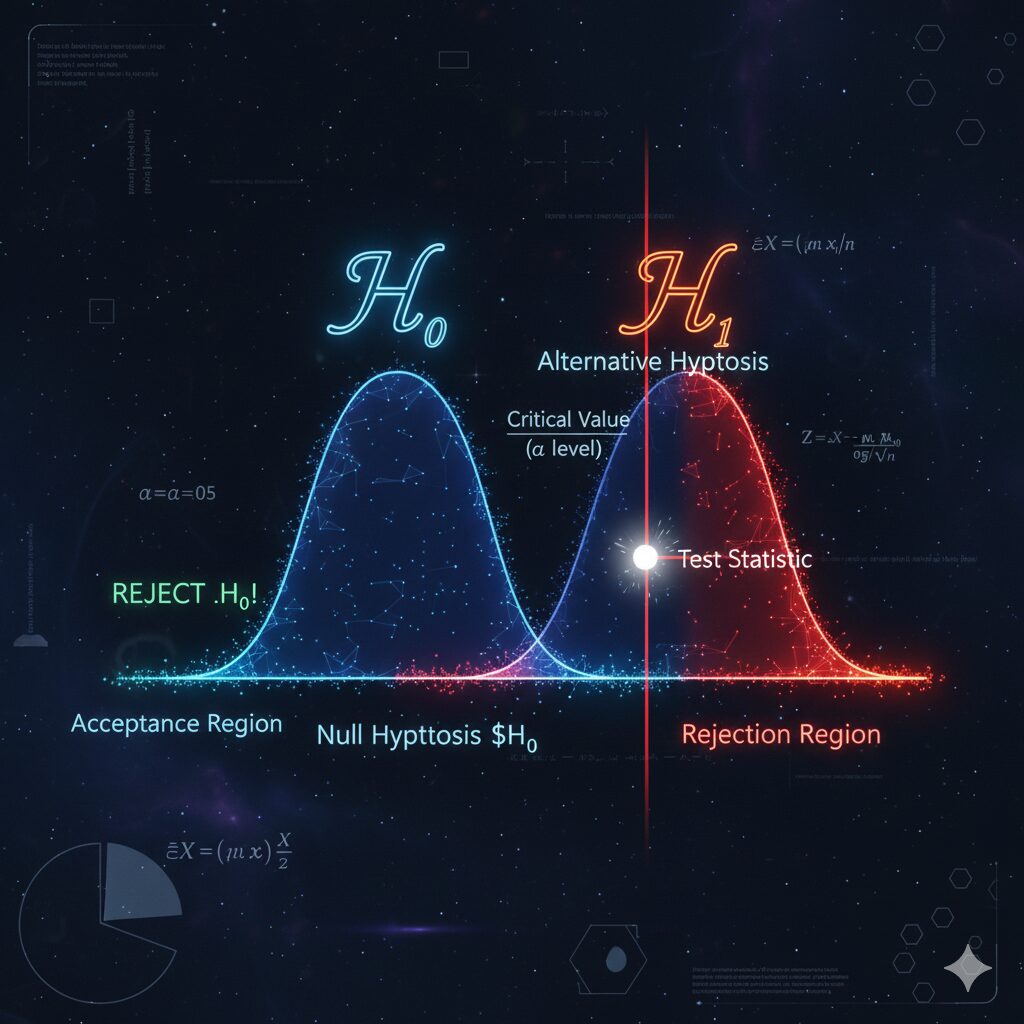
統計的検定

イェーツの補正を行うとカイ2乗統計量の値を小さくすることになり、棄却されにくくなるわけです。
尤度比検定
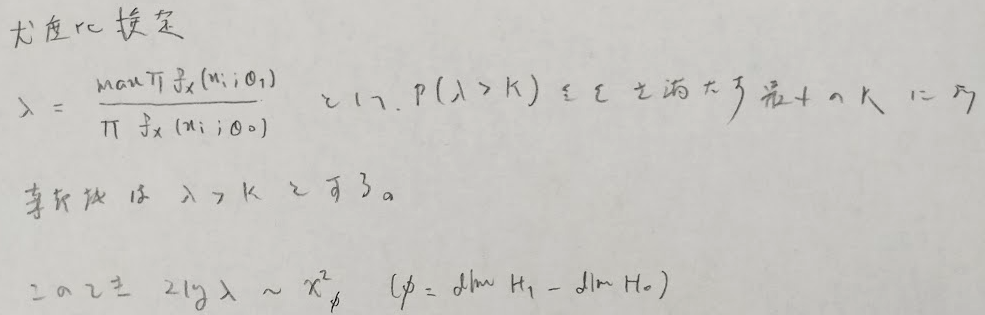

有限母集団
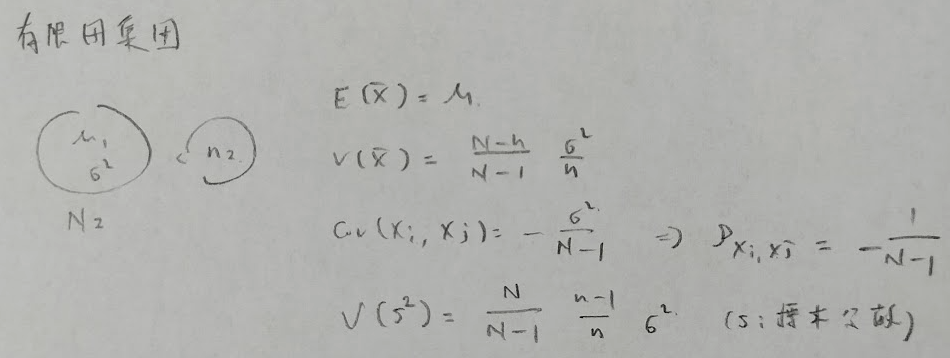
平方和は大きいので分散も大きい。つまり第1因子の分子はNが来る。(と覚える。)

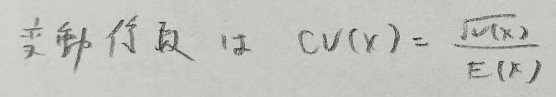
変動係数は単位の違うもの同士のばらつきを考える量なので、分母には期待値がきます。

層別抽出法に関する証明も行っておきます。

またQC検定1級の範囲になってしまいますが、関連公式として2段抽出法の公式もあります。

無限母集団の場合は、MとNを無限にすればOKです。また、M=mの場合は層別サンプリングで、N=nの場合は集落サンプリングとなります。
標本分布論
アクチュアリー数学:モデリング分野
モデリング分野はアクチュアリー数学において最も公式の数が多い分野です。ただの丸暗記ではなく理解を伴った記憶を目指しましょう。
回帰分析
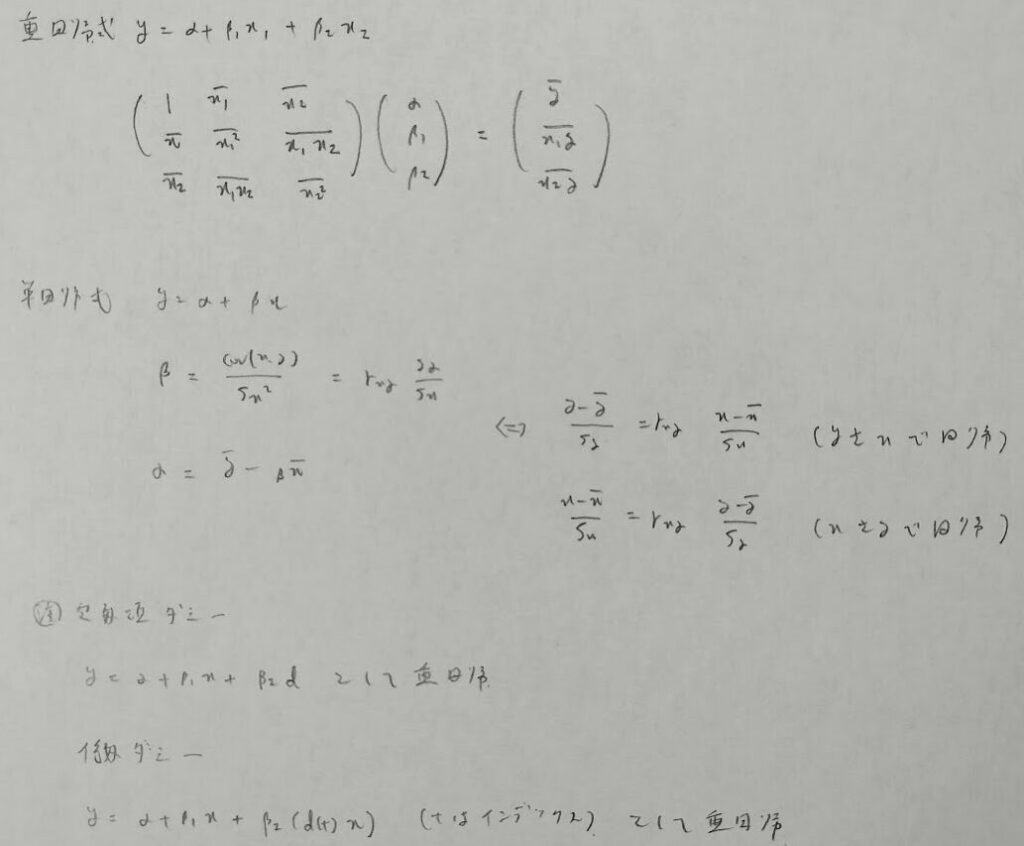
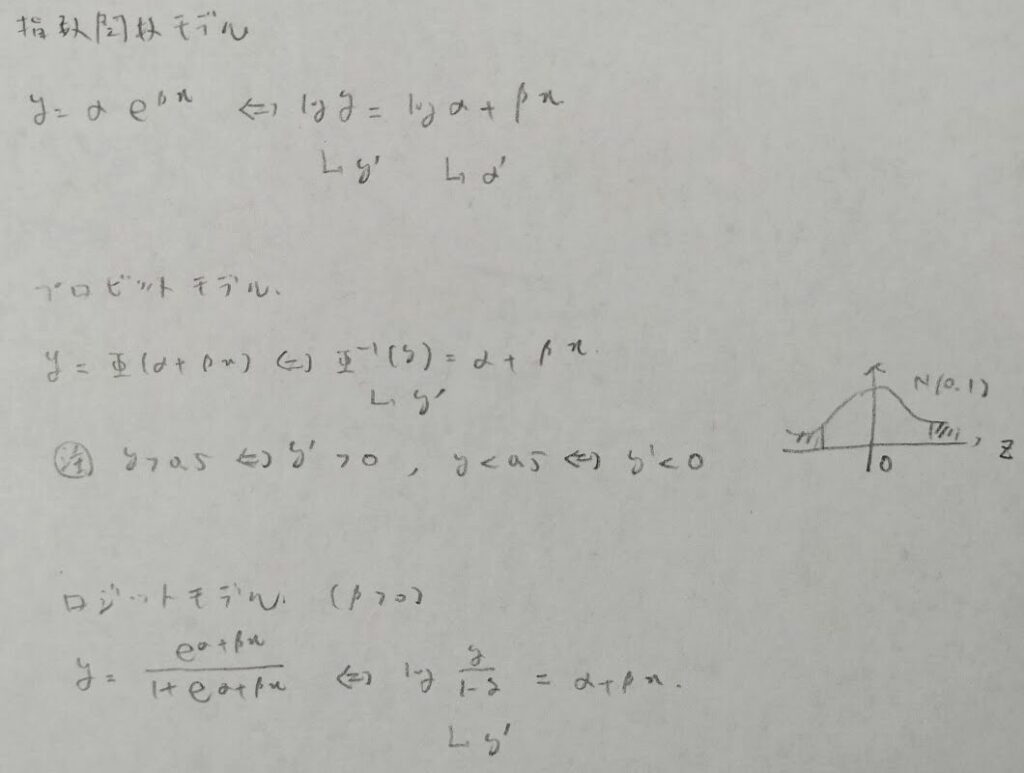
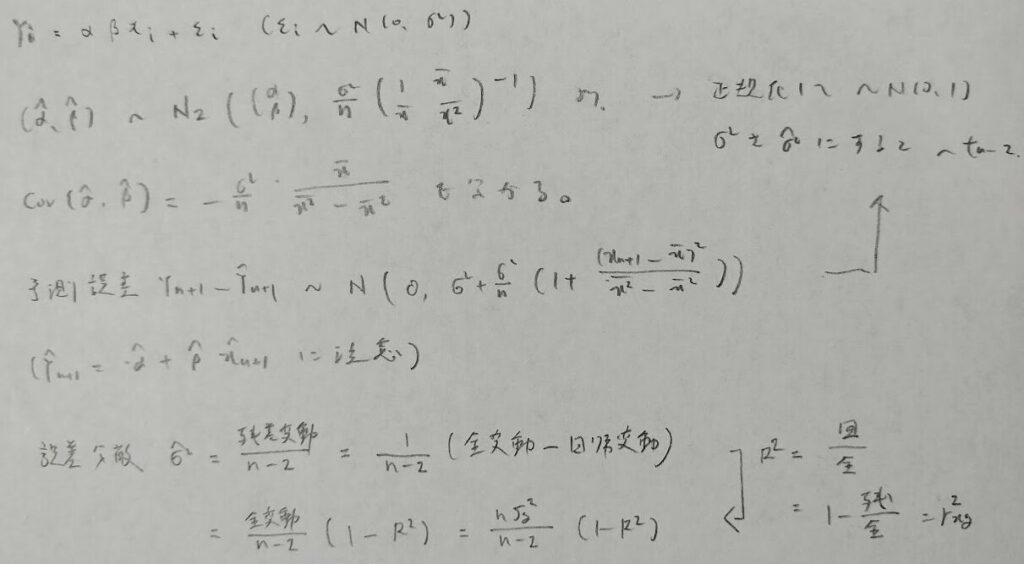
時系列解析

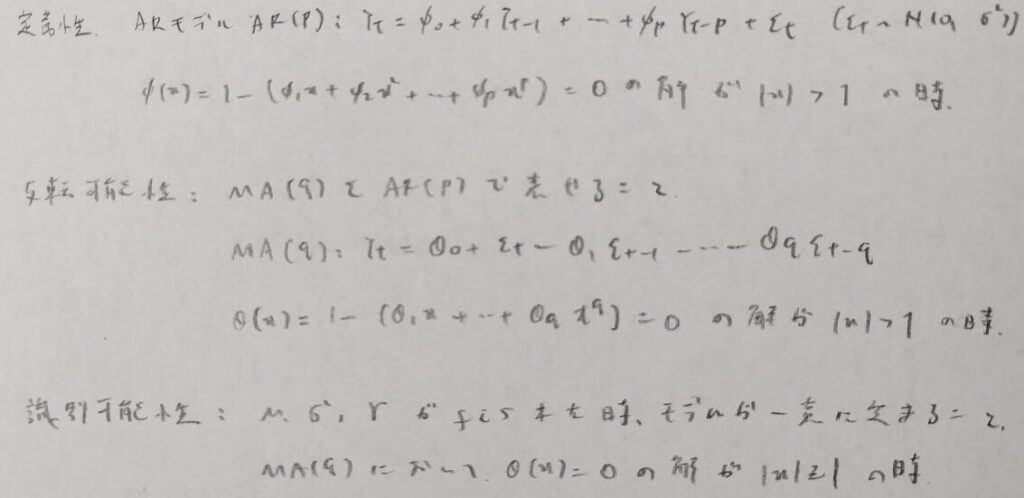

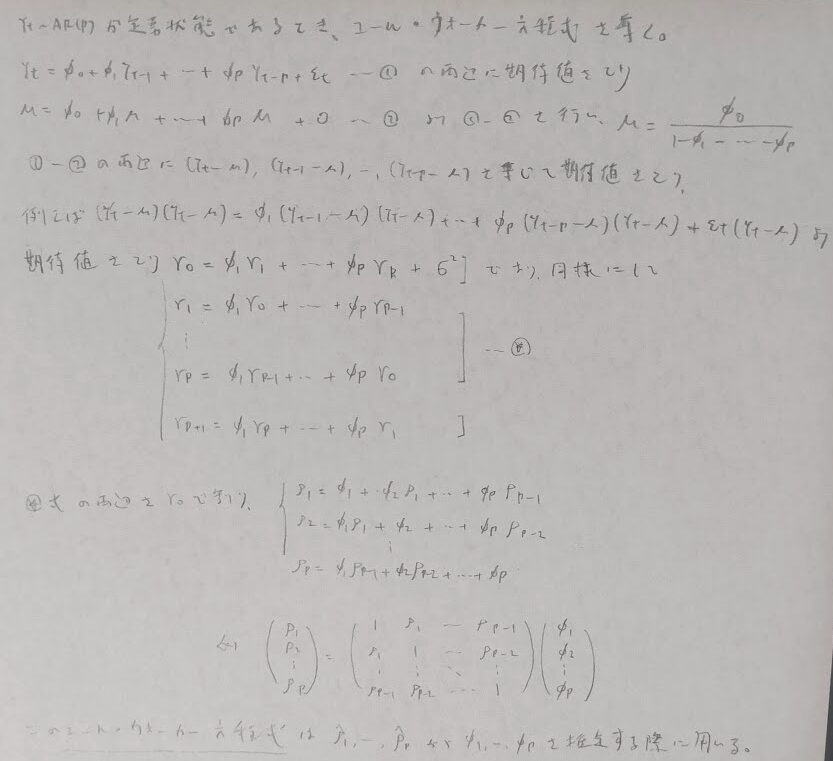

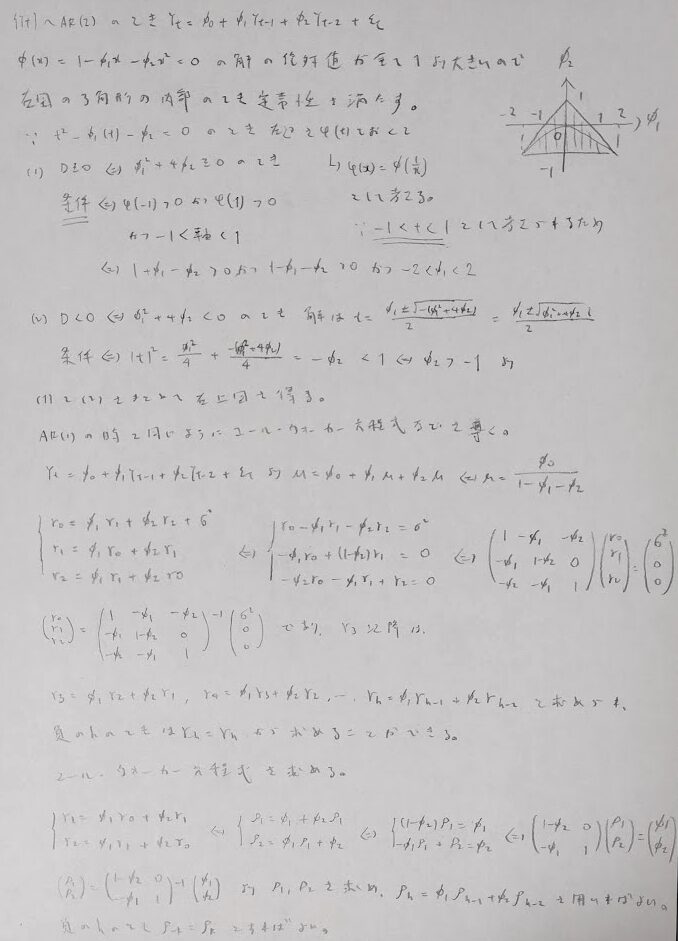




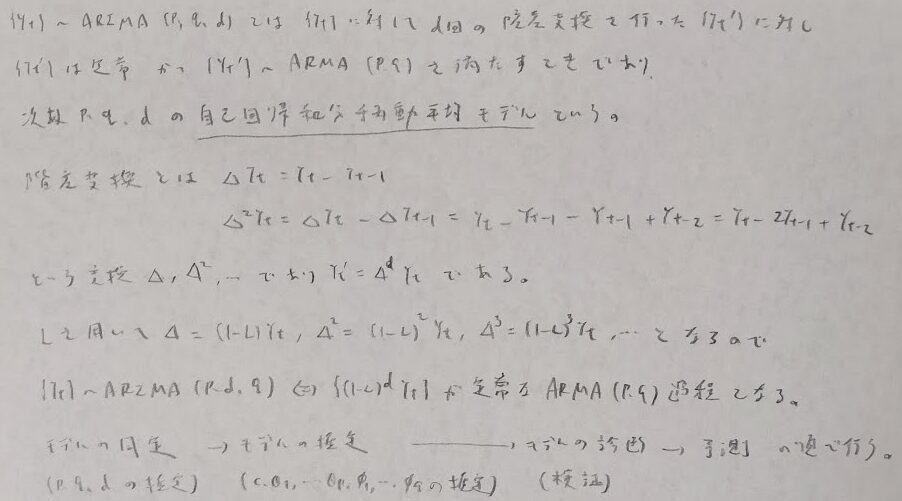
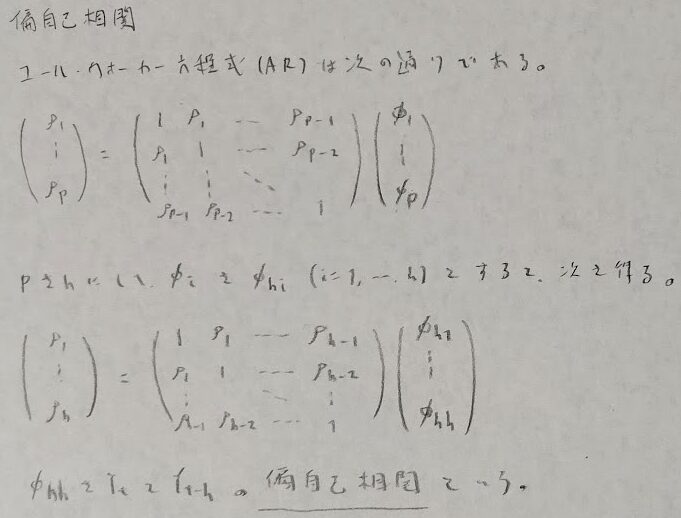
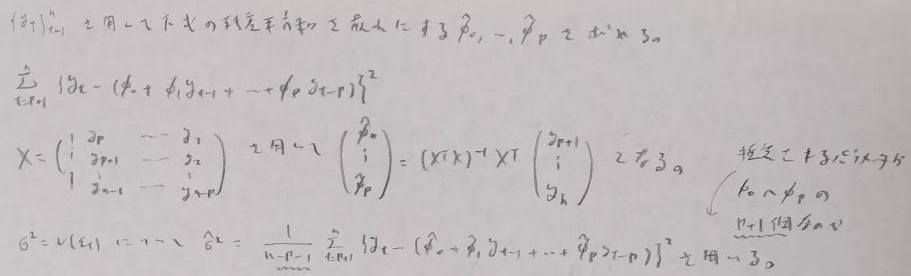
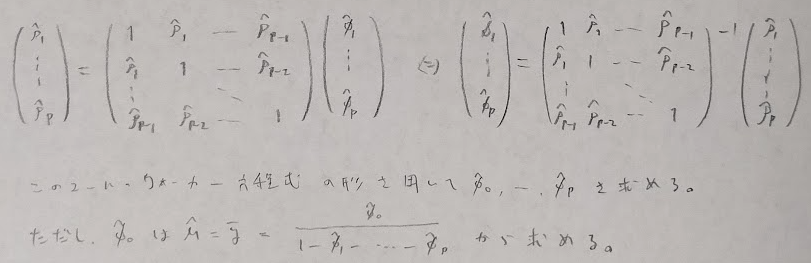

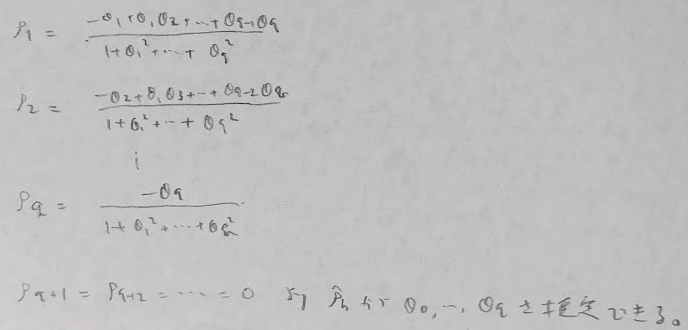
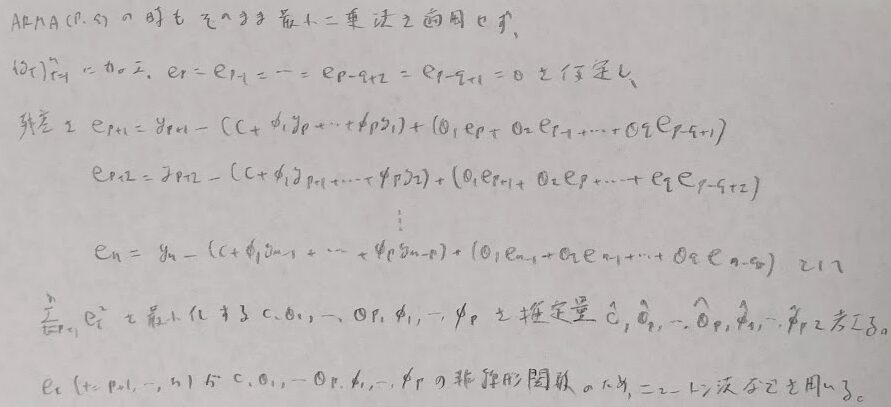
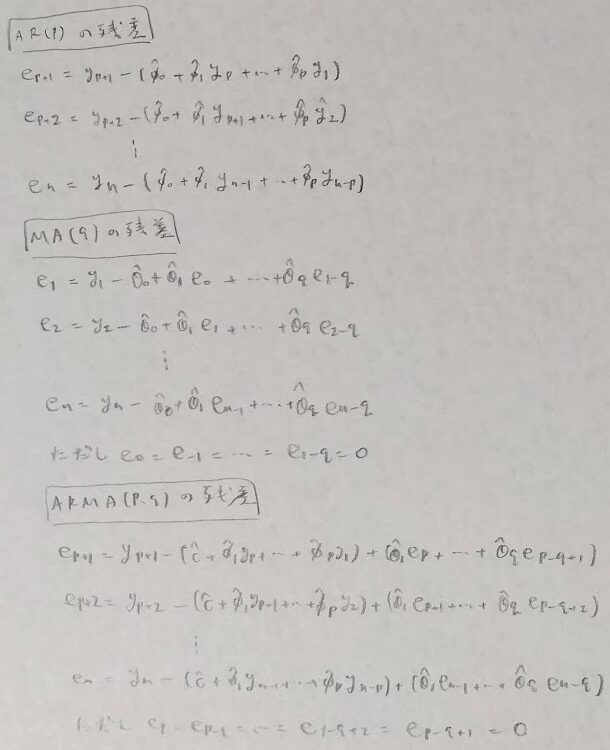

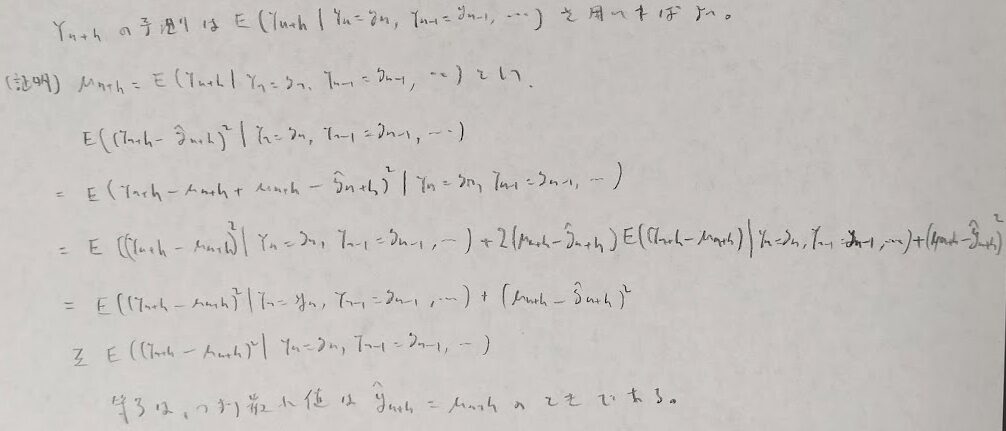
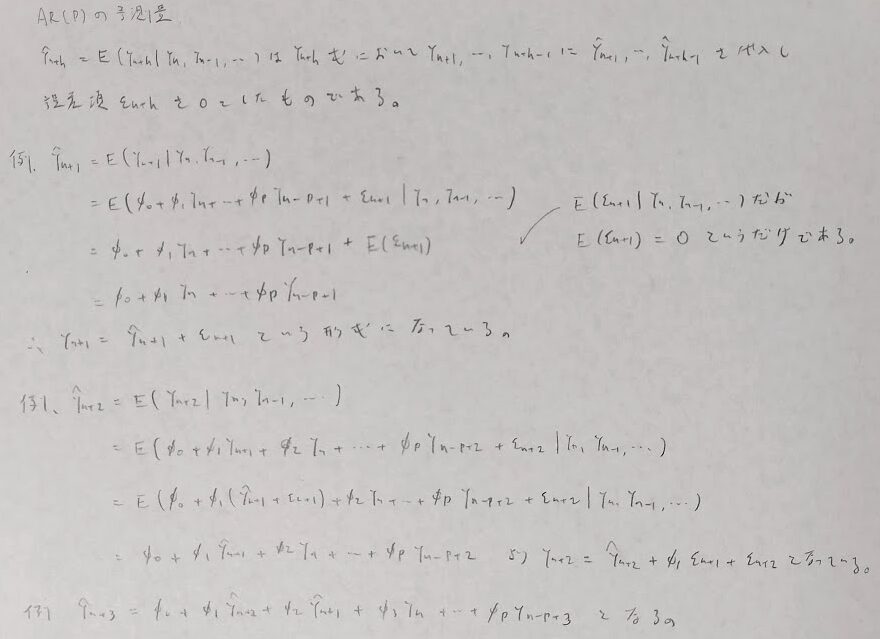

確率過程
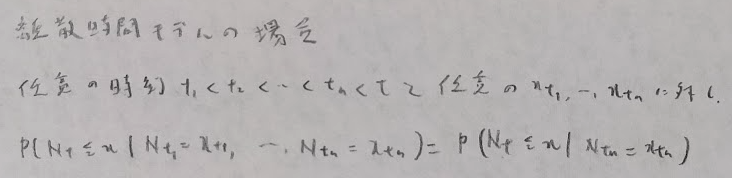
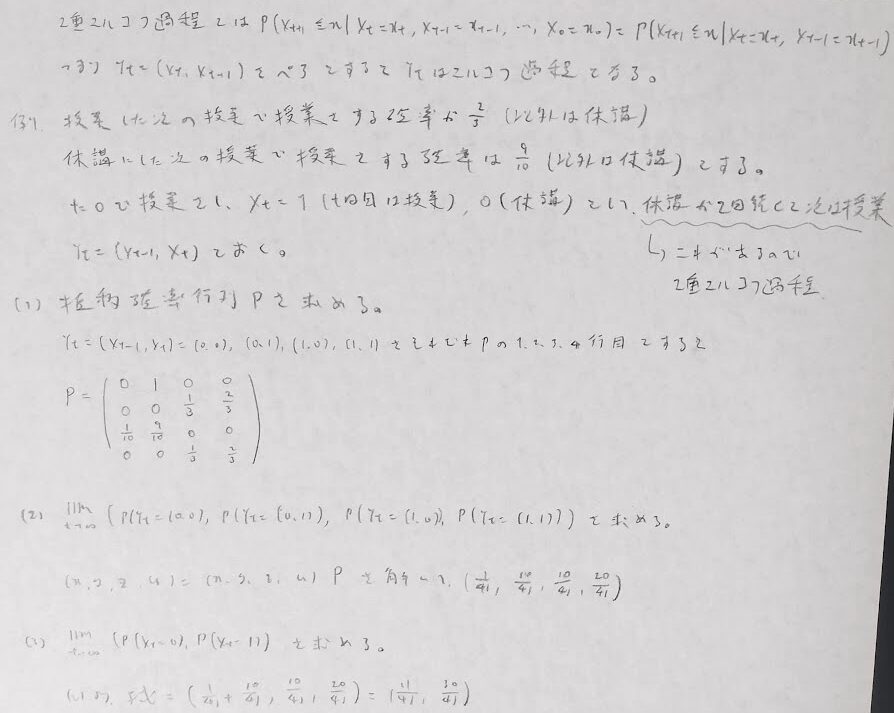
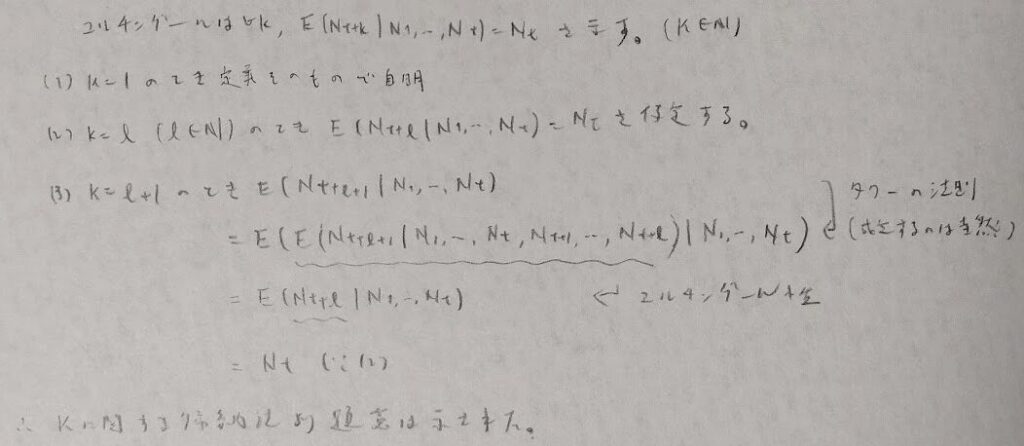
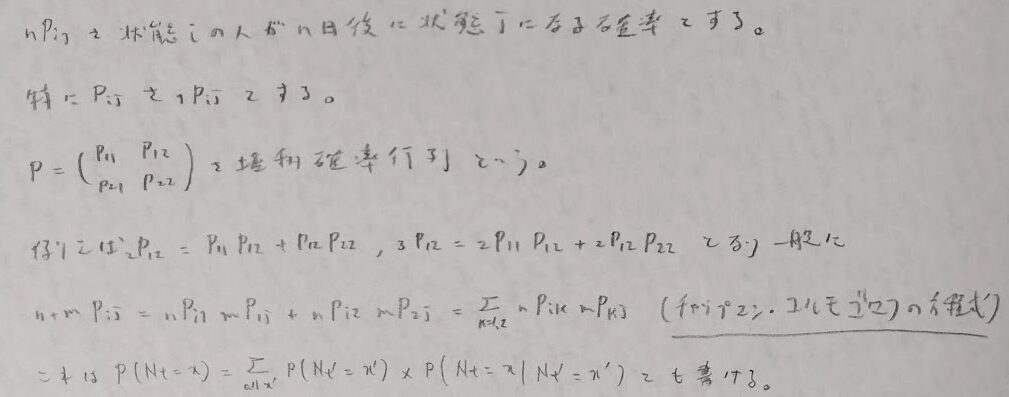
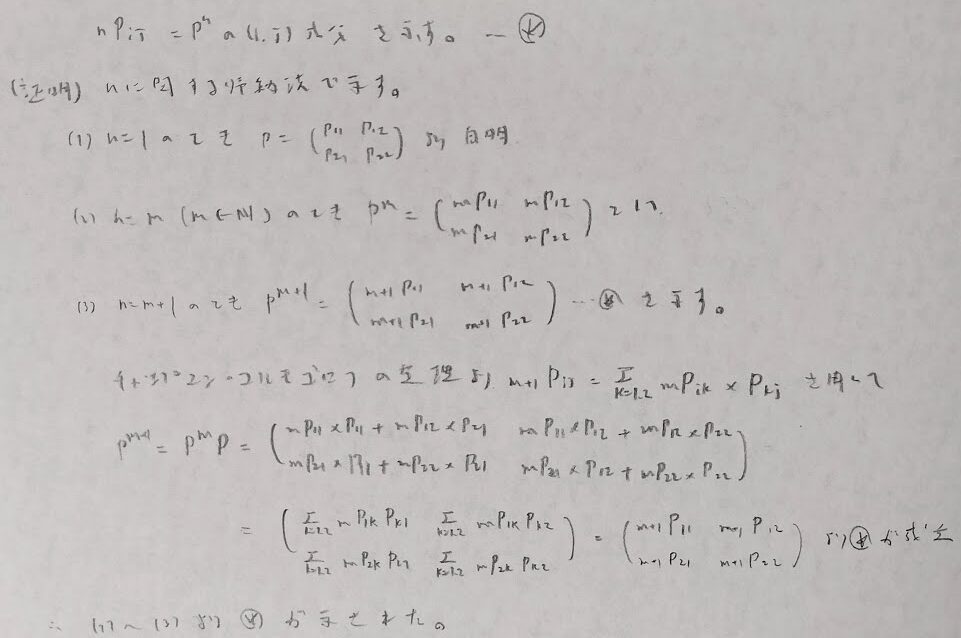
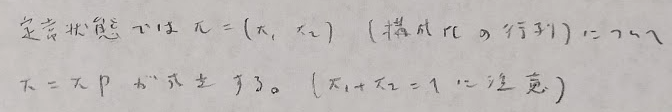
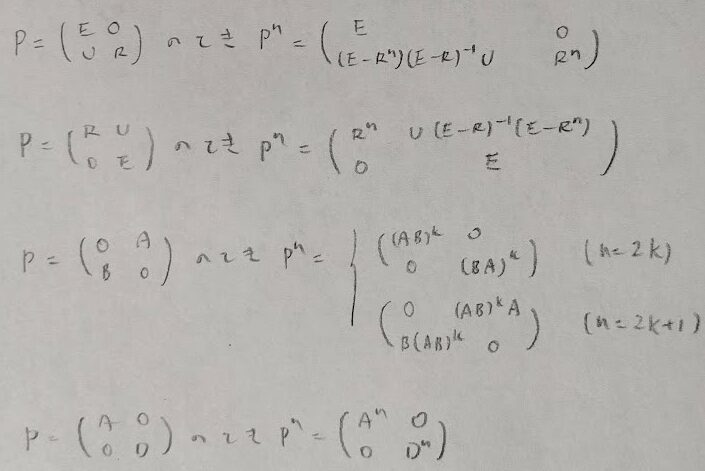
分からなくなったら実験で結果を推測できます。その際に、スカラーでの(1-r^n)/(1-r)は行列での(E-R^n)(E-R)^(-1)に相当します。

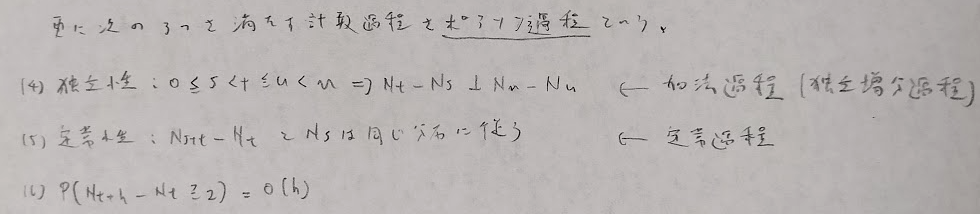
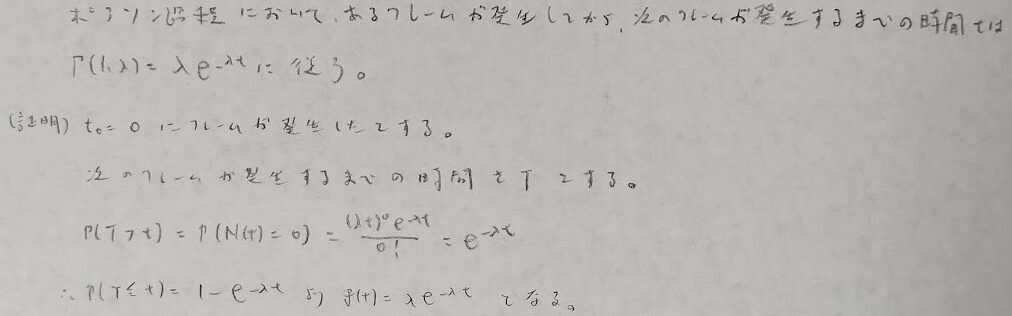
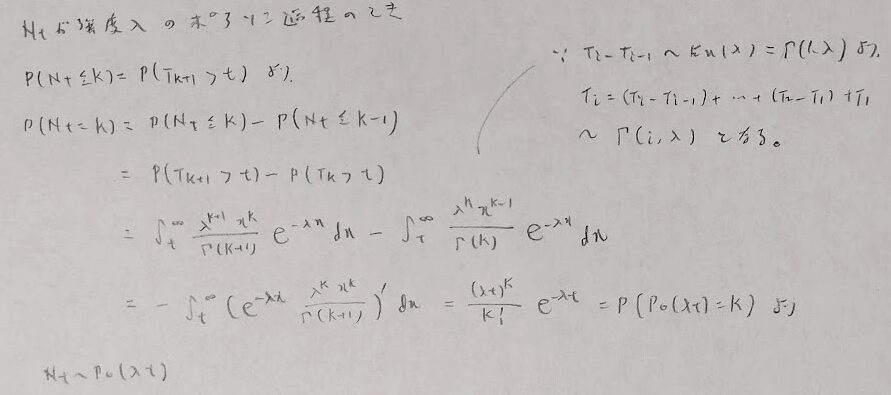



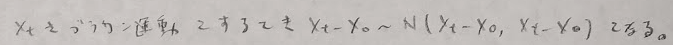
シミュレーション

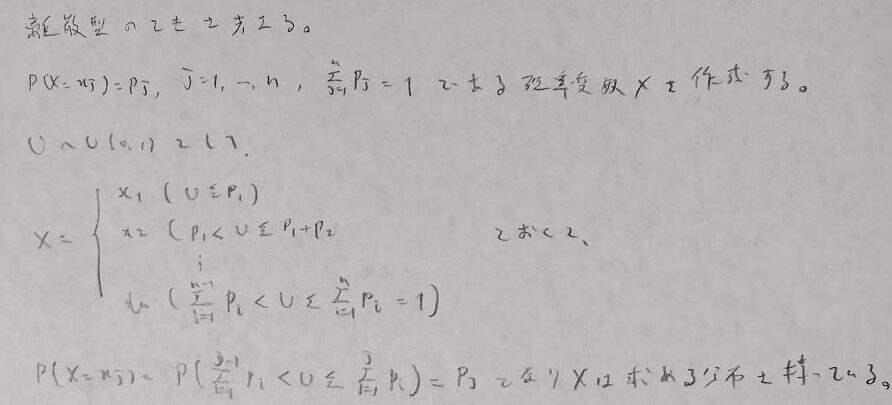
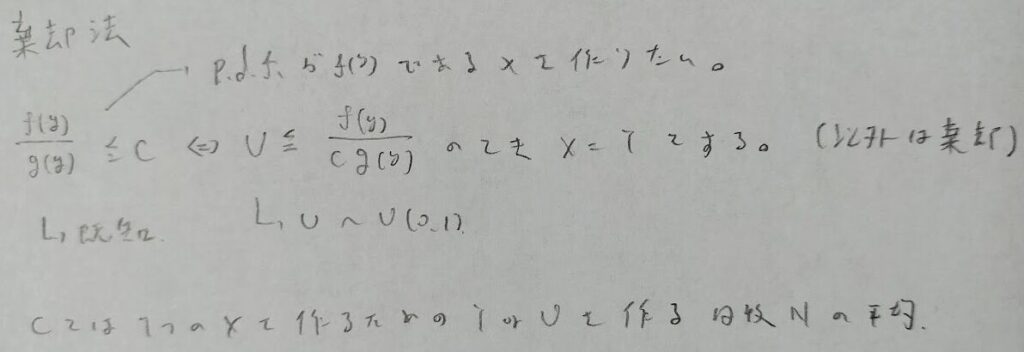
乱数作成の回数はパラメータCのファーストサクセス分布に従います。
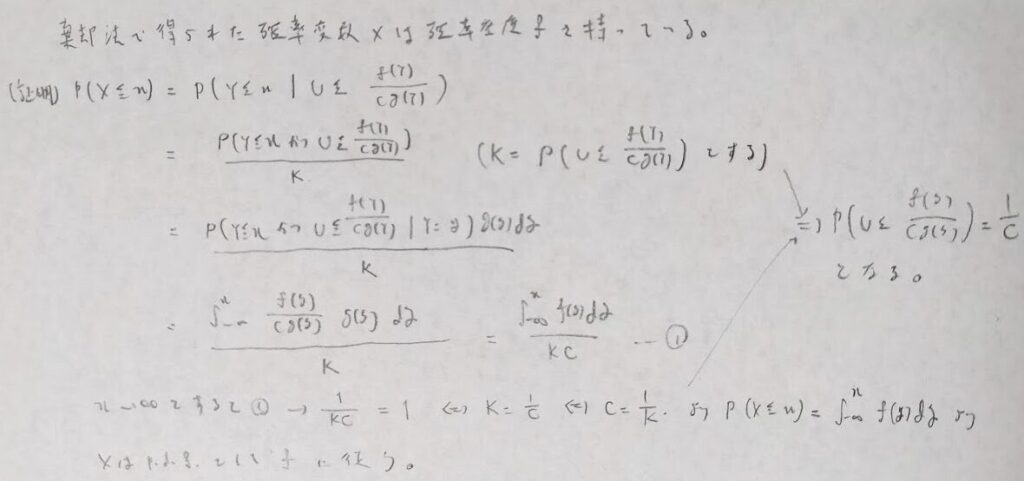
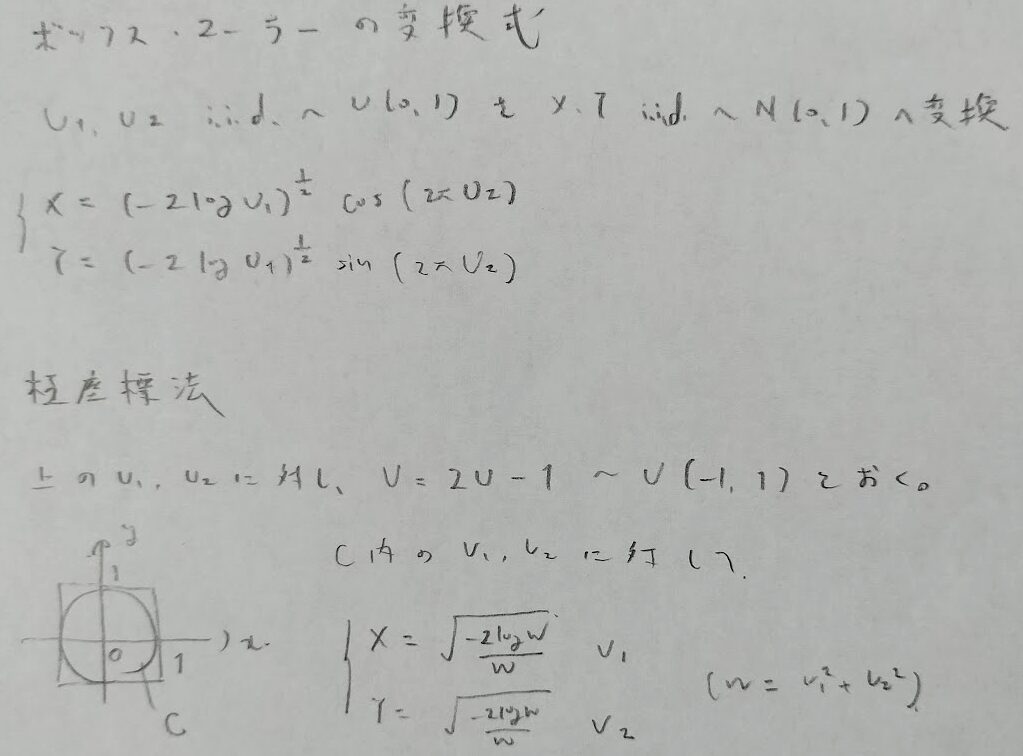


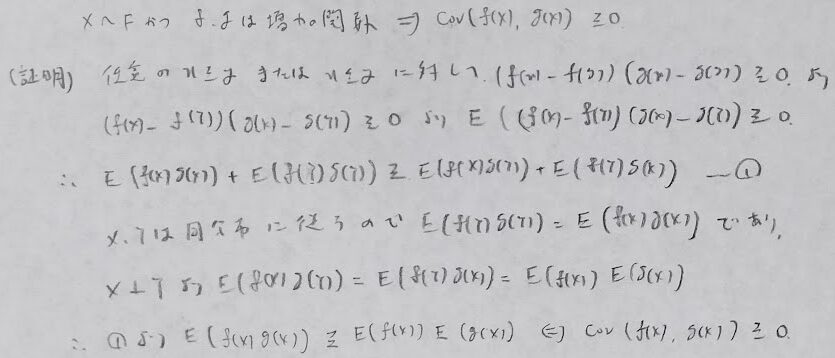
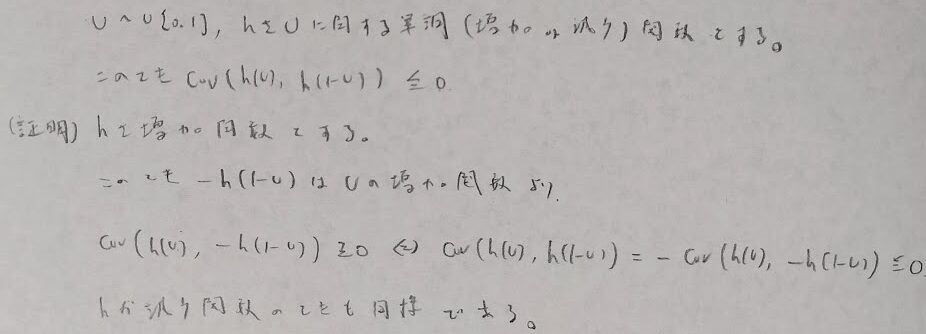
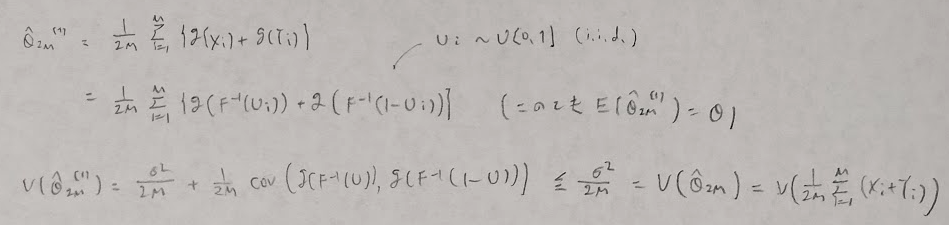
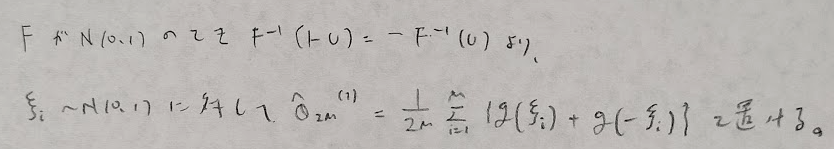
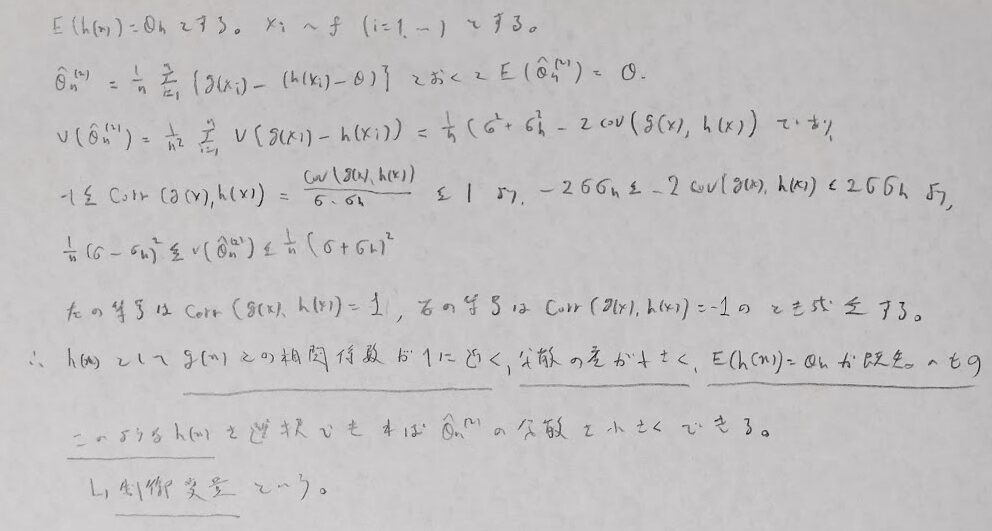

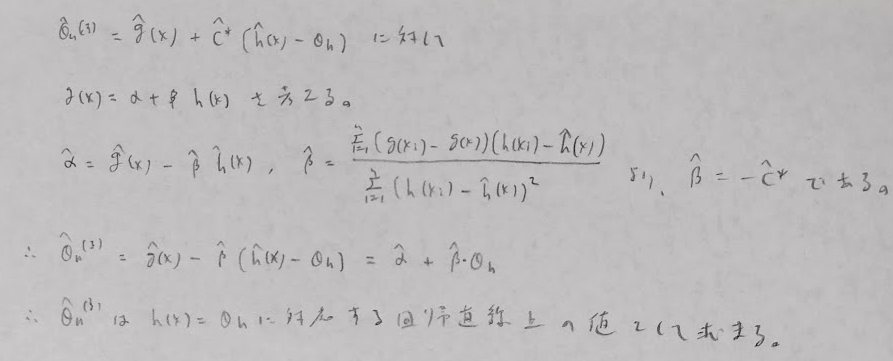
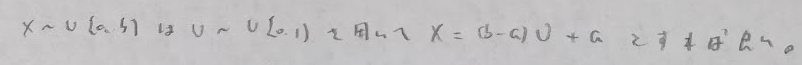

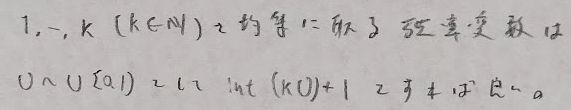





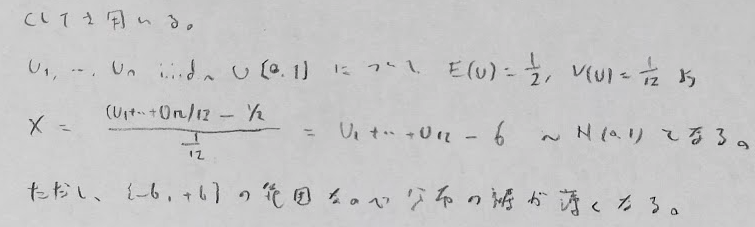



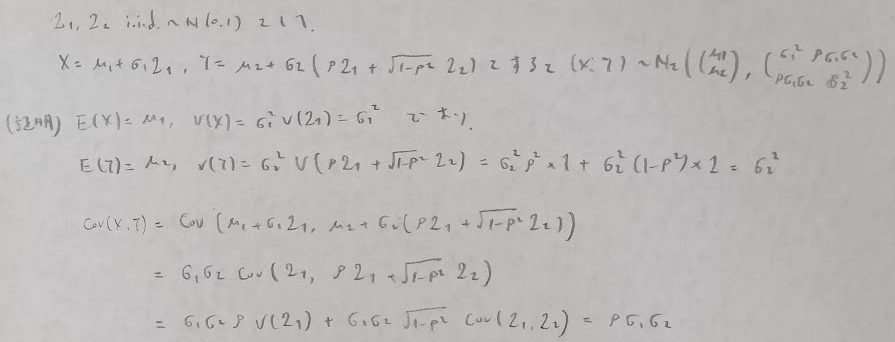
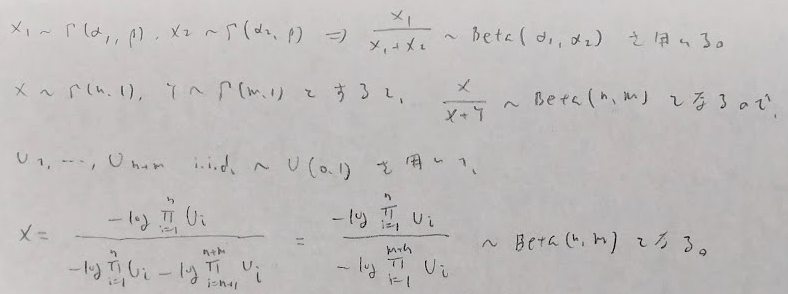
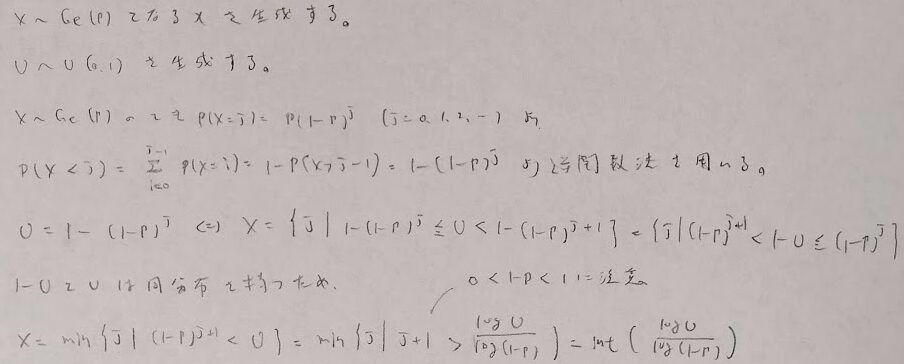
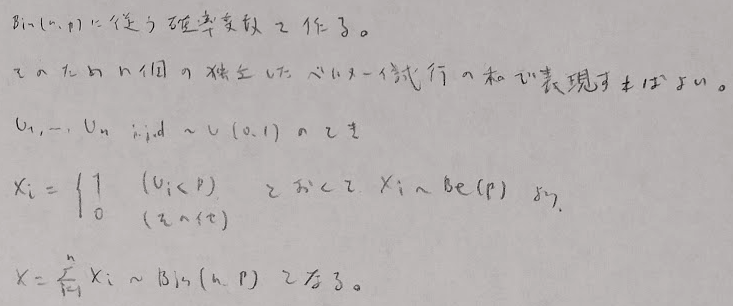
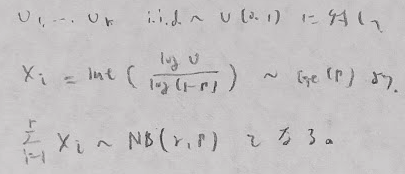
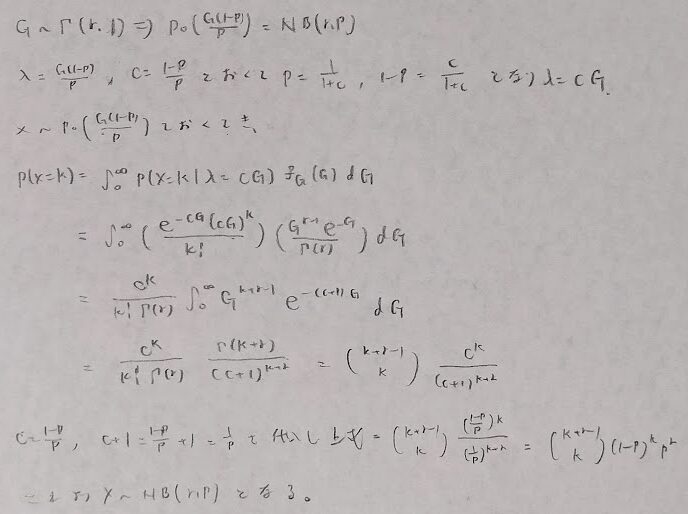

アクチュアリー数学:合否を分ける確率分野の過去問
平成10年度数学Ⅰ問1(8)追加費用の問題

平成17年度問1(12)成功を失敗と考える

かなりの難問です。2025年11月現在、類題は出題されていないタイプです。
平成9年度数学Ⅰ問4:指数分布との関連

平成10年度数学Ⅰ問4:バクテリア問題

ポアソン分布のパラメータを追っていくことがポイントです。また現時点のバクテリアの総数は、一体どこからやってきたのか?の着眼点を持つことが大切です。
平成16年度問3:歪度など

平成8年度数学Ⅰ問2:ファーストサクセス分布との関連

平成11年度数学Ⅰ問4:特性関数

昭和63年度数学Ⅰ問1(2)正規分布の確率密度関数

平成2年度数学Ⅰ問1(9)標準化

平成9年度数学Ⅰ問1(4)記憶保持平均時間

どこから手をつけるか困ったら、Xが従う確率密度関数においてパラメータの設定をしてみましょう。
2021年度問1(2)通話料金の期待値

平成5年度問4:公式利用

平成7年度数学Ⅰ問2:宝くじの問題

平成14年度問1(8)無限小数

無限小数の問題は繰り返しを意識した方程式の立式を考えます。
式が簡略化されていて分かりませんでした。もう少し行間を広げてください!
了解です。P=(1/6)×(1/6)+(1/6)×(1/6)×(2/6)+(1/6)×(1/6)×(1/6)×Pです。
平成16年度問1(3)ひっかけ問題

前半部分で1つの場合を引くことに注意しましょう。
平成7年度数学Ⅰ問1(3)イヤリング問題

確率変数の設定を意識しましょう。
イヤリング問題は初見ではかなり厳しいですね。
2020年度問1(1)赤玉と白玉

確率変数を複数設定するので難問です。類題は未出のため要チェックの問題です。
平成5年度数学Ⅰ問1(1)何から手をつけたら良いか不明の問題

平成3年度数学Ⅰ問3:多重積分

平成6年度数学Ⅰ問1(4)標準正規分布
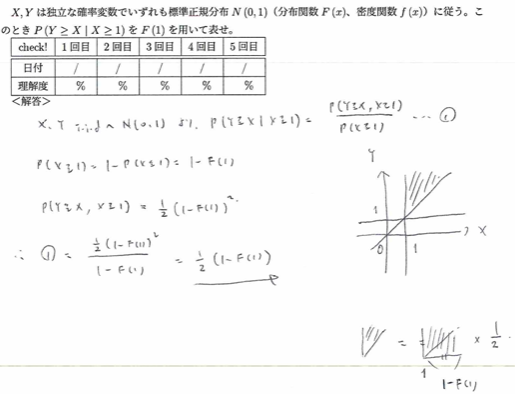
面積で考えます。条件付き確率の定義通り考えないとミスをしますのでご注意ください。
この問題も本番でこのようなうまい方法を思いつけるか?と言われれば難しいと思います。そのため下記に正攻法を書いておきます。
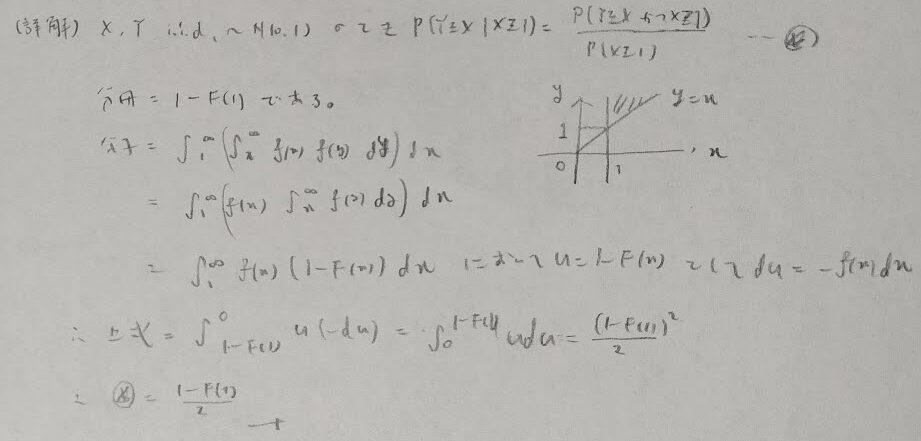
2019年度問1(2)3つの点

2022年問1(2)コイン投げ

平成元年度数学Ⅰ問1(7)入院患者数

平成4年度数学Ⅰ問3:分布関数

平成6年度数学Ⅰ問3:誤植問題

平成8年度数学Ⅰ問1(4)複合分布の分散

平成9年度数学Ⅰ問1(3)産卵

平成11年度数学Ⅰ問1(6)男の子がいる確率

平成6年度問1(1)リセットの区切り

平成21年度問1(1)2元型

平成15年度問3:2次元ランダムウォーク

平成14年度問3:蜘蛛問題
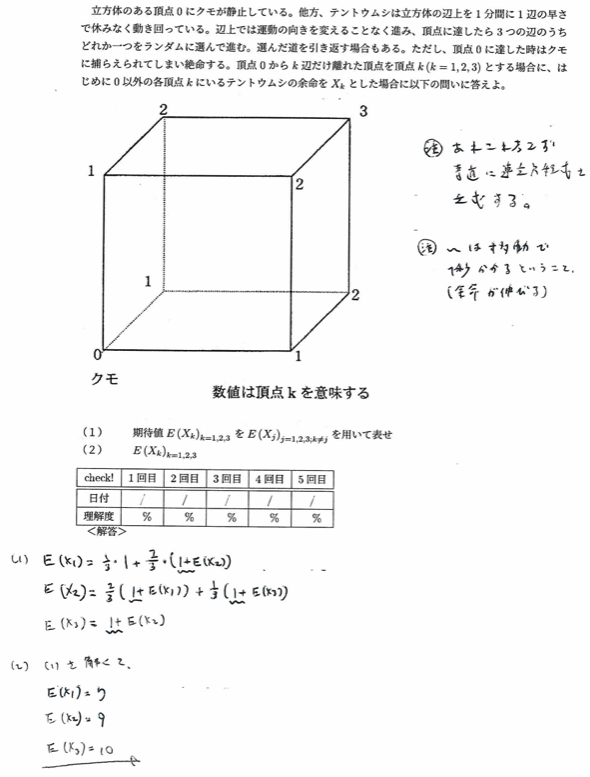
平成17年度問3:飛越禁止

平成11年度数学Ⅰ問1(7)鉢合わせ

2020年度問1(2)離散と連続の期待値

平成6年度数学Ⅰ問1(2)三角分布に似た分布

本問も当然、zx平面を用いて積分区間を考察することもできます。
平成元年度数学Ⅰ問1(8)鋭角三角形
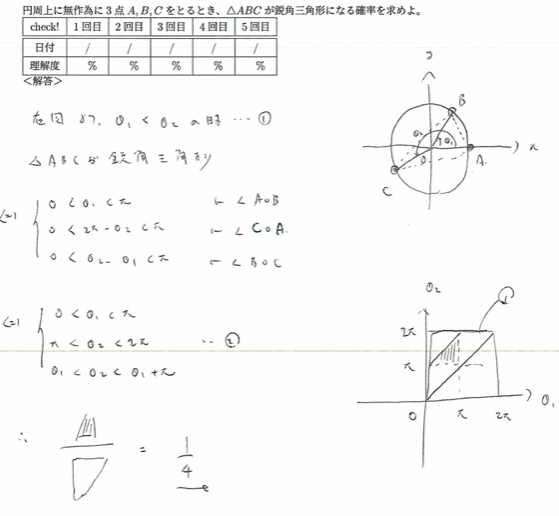
平成5年度数学Ⅰ問4:三角形ができる確率
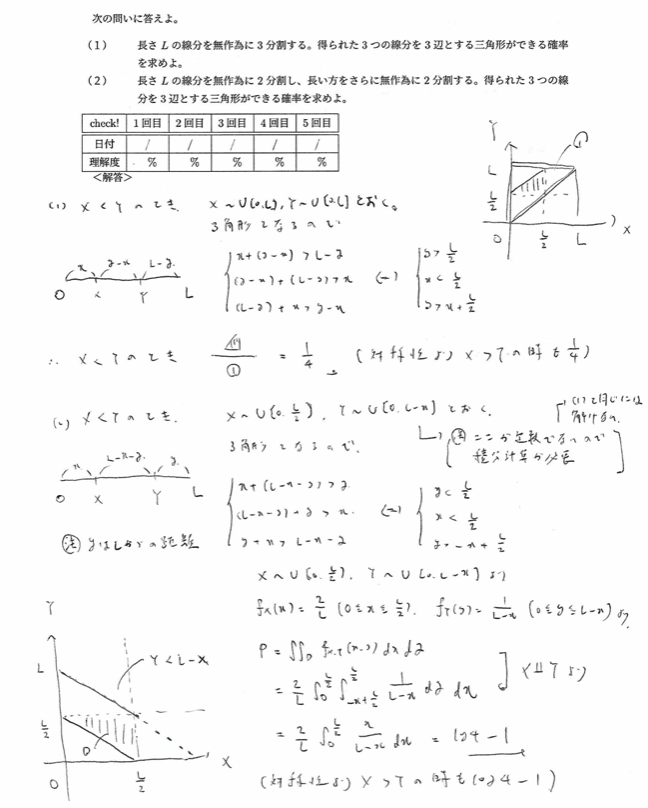
平成6年度数学Ⅰ問4:半円
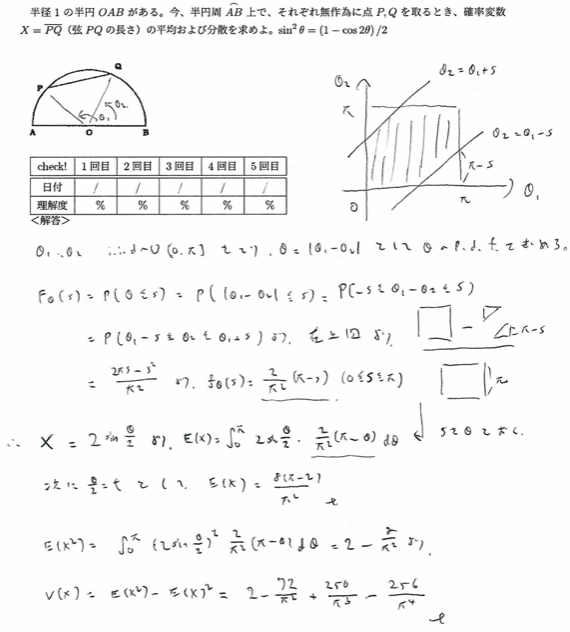
平成8年度問1(2)回転する長方形
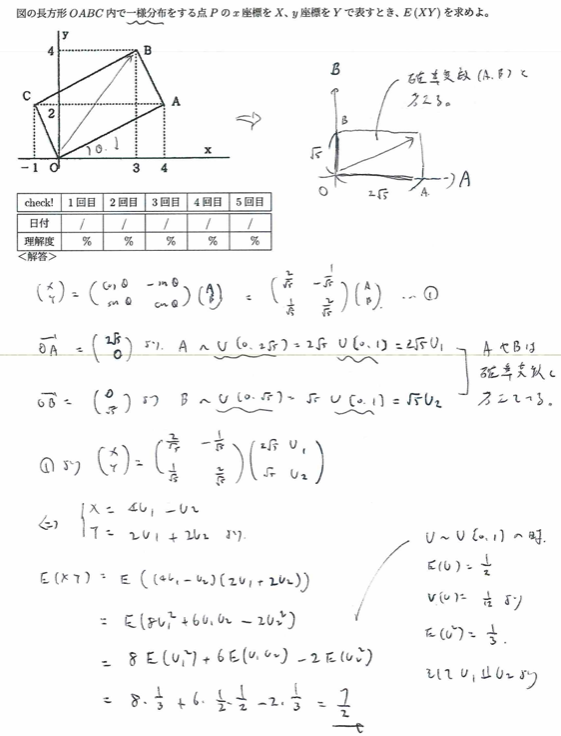
平成16年度問1(6)半円内の直角三角形
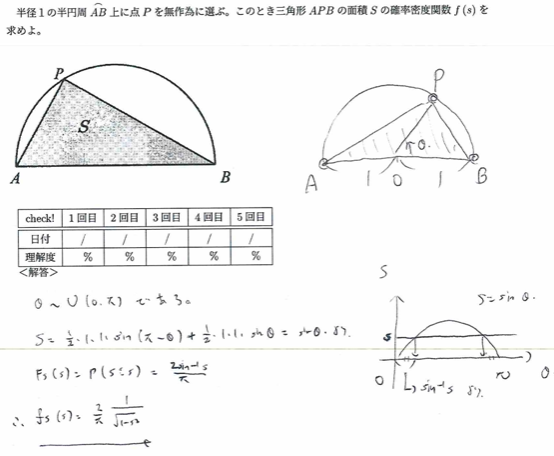
平成18年度問1(5)三角形の面積の期待値
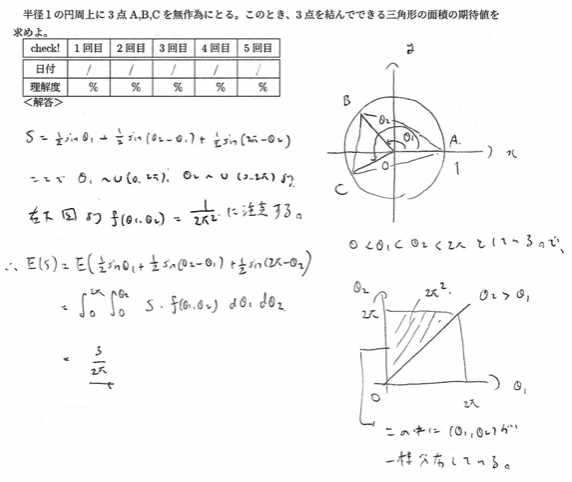
2024年度問1(3)正三角形

平成3年度数学Ⅰ問1(10)四捨五入

平成5年度数学Ⅰ問1(2)二次方程式が実数解を持つ確率
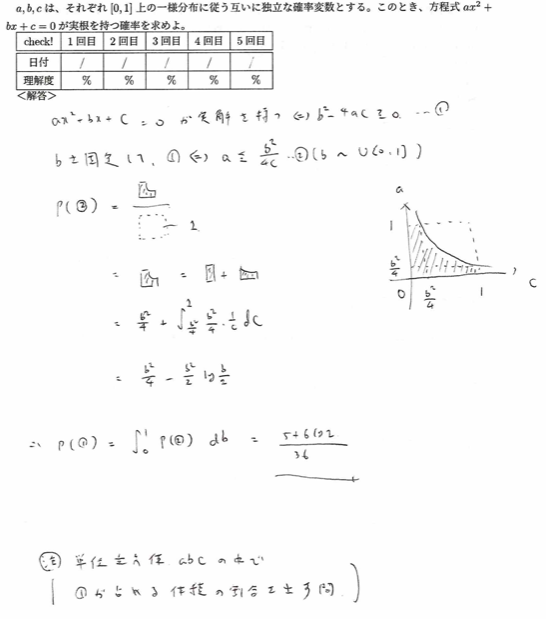
平成2年度数学Ⅰ問3:コンデンサー

2020年度問1(3)分布関数経由

平成元年度数学Ⅰ問1(10)複合分布との融合

平成2年度数学Ⅰ問2:待ち時間の分布

平成5年度数学Ⅰ問1(3)通話料金

平成14年度問1(7)平均の誤差
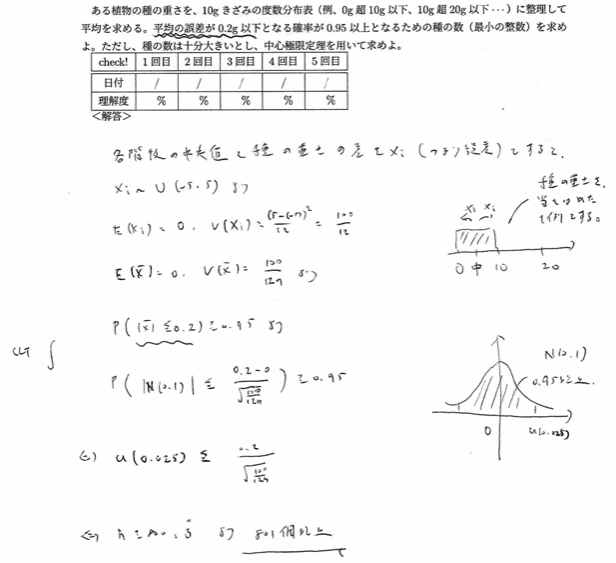
平成15年度問2(7)四捨五入

平成16年度問1(6)五捨六入

2022年度問1(4)カブトムシの再来

2020年度問1(4)七捨八入

二項分布の問題であることに注意しましょう。また、僕は本問を解いた時に作問ミスか?と思いメモしましたが、そんなことはなかったです。なぜなら後半の問題はXkの値の和より、Wkは小さくても0未満にはならないからです。
2023年度問1(5)計算量の増加

アクチュアリー数学:合否を分ける統計分野の過去問
平成5年度問3:変化球

平成6年度問1(5)最短の信頼区間
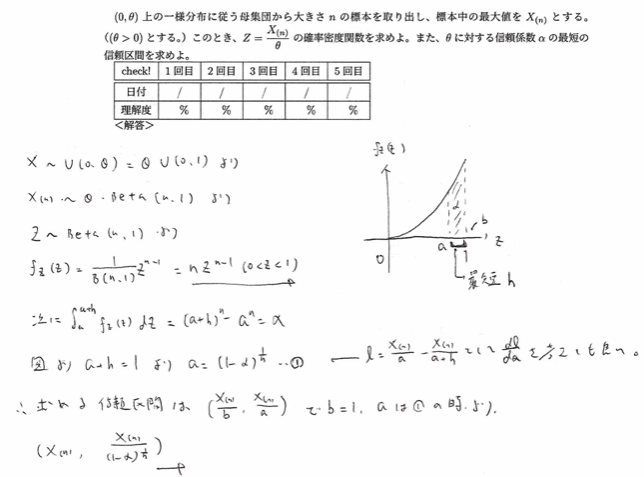
難問です。最後のあたりが難しいと感じます。ポイントは確率密度関数の形より1に近い方が信頼区間は最短になる事実を用いています。
最後の信頼区間の答えのところがわからないので、追加の解説をお願いします。
まず信頼係数がαより、P(a≦X(n)/θ≦b)=αなので、この()の中をθについて解いた式に、上の解答にあるa,bを代入すれば答えです。
今回のようなX(n)/θのような関数をθに関するピボットと言います。この名称はアクチュアリー数学では範囲外です。
平成25年度問1(5)変化球

平成13年度問4:負の二項定理

2021年度問1(6)最尤推定量最難関
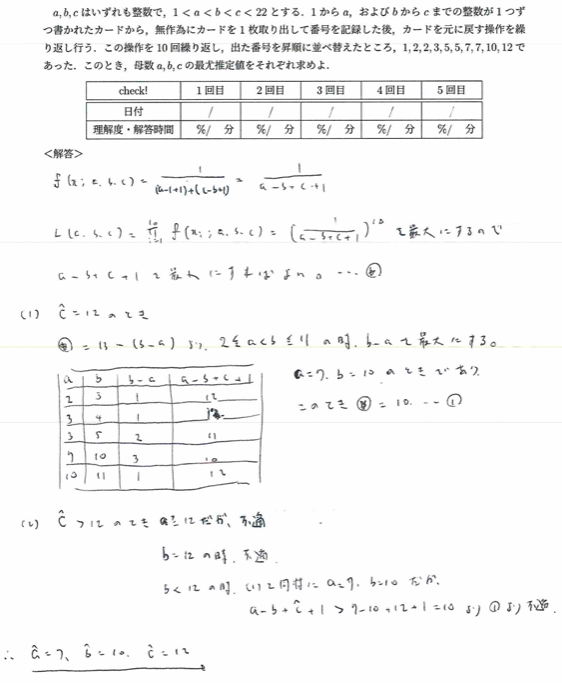
平成6年度問2:ガンマ分布の高次モーメント

平成11年度問1(6)一様分布

定義に従う新傾向問題

平成元年度問1(5)誤差

平成7年度問4:信頼区間の幅

平成11年度問1(5)最小の標本数

平成20年度問1(6)支持率

全体の支持率と全体の期待値の違いに注意しましょう。
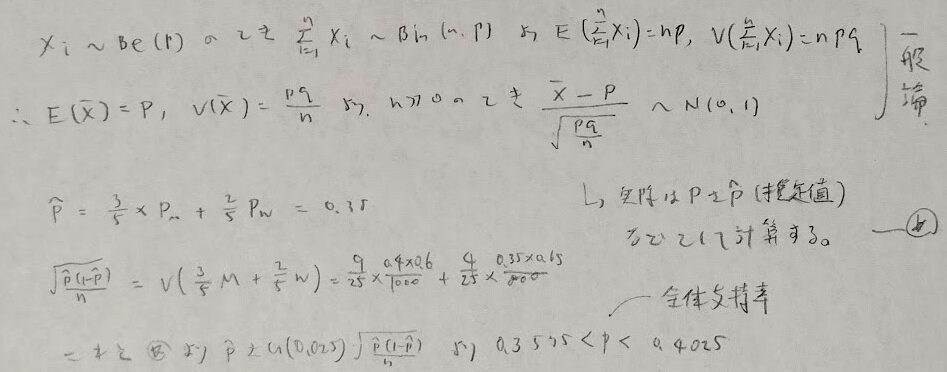
詳しいことを抜きにして男性をMで女性をWとして簡略化しています。
2021年度問1(7)金額分散

平成21年度問1(7)測定された分散

求める内容が、どの分散か?に注意して考えましょう。要するに誤差を含んだものを求めるのか、誤差なしを求めるのか?の判定が大切です。
最後のまとめる作業は、X1+X2+…+X100という統計量を考えており、互いに独立な変数なことを考えると100倍すれば答えが出ることになります。決して10000倍ではありません。その場合は1本のジュースの量を100倍にしたという場面です。
平成3年度問2:典型問題

典型問題ですが難易度は高いです。近年の小問集合に頻出のタイプです。混乱をしないように練習しておきたい問題です。カイ2乗分布を作り出すことがポイントです。本問は年度を追うごとに他の問題タイプとの融合が始まります。ベーシックなタイプの本問をしっかり解けるようにしておきたいですね。
平成13年度問2(9)z値

標準正規分布ではz値の絶対値が3に近づいたら、上側確率はほぼ0になります。すなわちz値が±3より外れる可能性は極めて0であると言えます。
ある値離れたという表現は+の場合とーの場合を考えるのが定石ですが、対称性より一致することがわかります。そのため解答では+の場合のみ考えています。
典型問題と思いきや、かなりの良問でしたね。
平成元年度問1(9)(10)検出力最大

右側検定の棄却域はある値よりも大きいということです。まずは棄却域を設定しましょう!
平成4年度問1(3)最良の検定方法

有意水準の条件のもとで、検出力が最大となる検定が良い検定です。
平成7年度問1(2)混合問題

まず棄却域の設定をしましょう。検定問題でわからなくなったらこの方針が鉄則です。
平成9年度問1(1)変化球

重積分するのは同時分布ですのでご注意ください。基本的ですが焦ると処理不能になります。
非常に良い問題です。2025年11月現在、類題の出題はありません。
平成9年度問2:抜取検査(最難関)

類似問題の中では最難関です。とても複雑な設定なので、帰無仮説と棄却域の設定をしっかりと行いましょう。96%以上と言えるか→96%であればOKなので対立仮説を96未満とするなどの考えが大事です。(2)では対立仮説を96未満と設定していきます。
平成10年度問1(1)典型問題

平成10年度問1(2)対立仮説

対立仮説が分かりにくいので、やや難しいですが2025年現在のレベルでは基本問題です。
平成29年度問1(7)分析問題

問題文から帰無仮説をこのように設定できるか?が勝負の分かれ目です。やや意地悪な書き方だと感じます。
ここら辺が検出力系の問題の最高到達点です。問題の内容的にQC検定1級の内容に近いです。しかしこれ以上難しくすると試験にならないと判断にしたのか、今後は違った方向性で難易度を上げています。
2022年度問2(2)棄却域

2022年度はアクチュアリー数学最難関の年です。本問は棄却域の設定で最も難易度が高い難問です。
平成7年度問1(3)推定量の分散
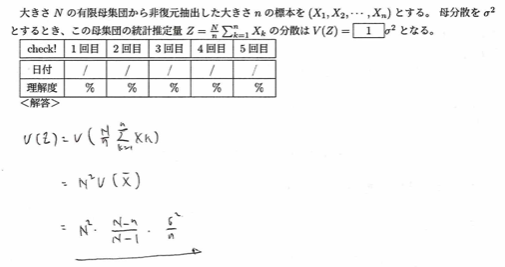
このようなパターンでは標本平均と推定量との間の関係を考えます。
平成2年度問1(1)母分散を求める

この問題の母分散は、1〜13のカードから一様に1つを取り出す時の状況を考えればOKです。別解も追記します。
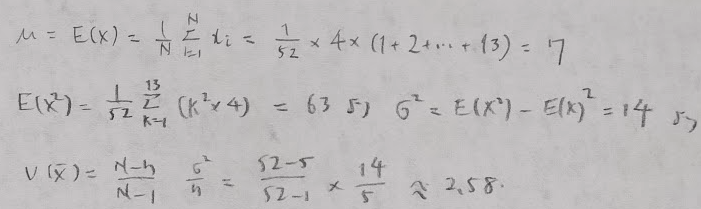
平成4年度問1(4)母平均も求める

対称性がない分だけ、前の問題よりも複雑な設定ですので別解も追記します。
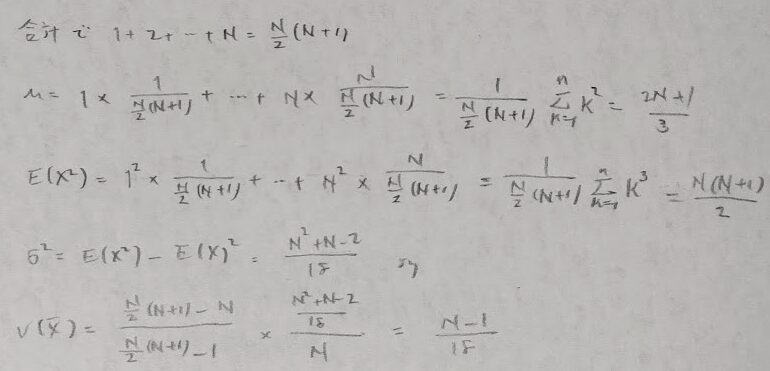
平成29年度問1(8)比例抽出法

平成8年度問1(4)変動係数

総人口と総人口の推定量などを文字で設定するところから開始です。いつもの標本平均には総人口の推定量を用います。
平成28年度問1(5)歪度のような式

平成28年度問3:ガンマ分布と一様分布

平成3年度問1(5)ベイズ推定値

積分範囲は座標平面にグラフを書けば判明します。
2023年度問2(1)メジアン
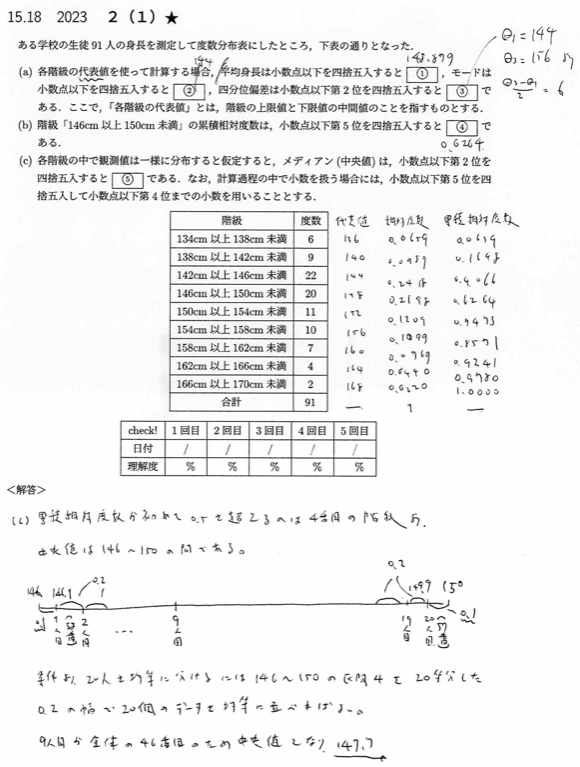
直感的には中央値の順位が91/2=45.5より、答えは146+4((45.5-37)/20)=147.7です。
アクチュアリー数学:合否を分けるモデリング分野の過去問
平成25年度問1(10)定数項ダミー

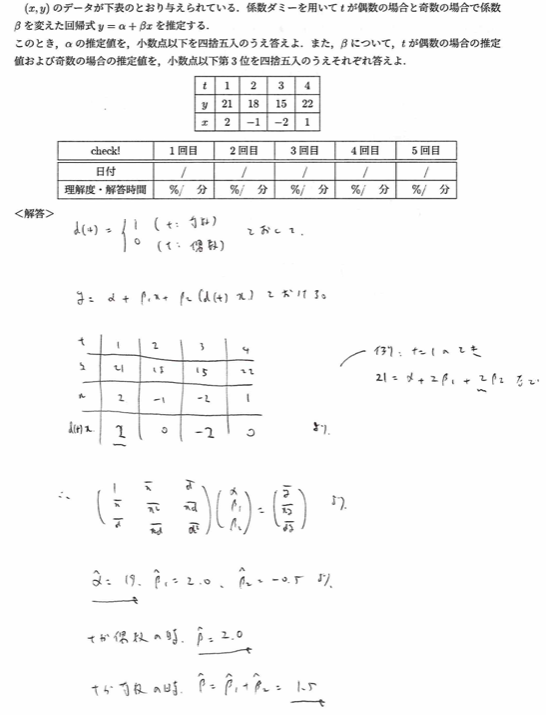
2020年度問1(9)係数ダミー
平成21年度問1(10)ロジットモデル

平成29年度問1(9)プロビットモデル

2022年度問2(4)指数関数モデル

時系列解析の問題は、暗記で押し通そうとするとどこかで無理が生じます。本記事前半にて時系列解析の論理の流れを掴みましょう。
平成17年度問1(3)AR(1)モデル

2024年度問4:長文問題


2020年度問1(10)MA(∞)モデル

2019年度問1(11)増分性

2022年度問2(6)条件付き期待値

平成17年度問1(11)標準ブラウン運動
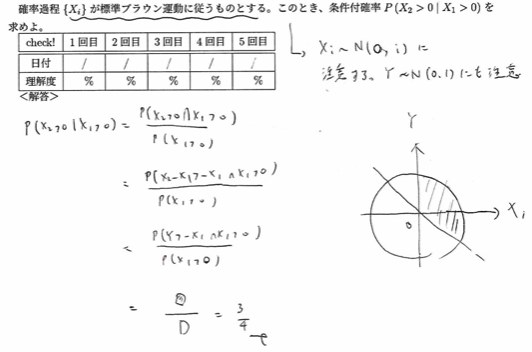
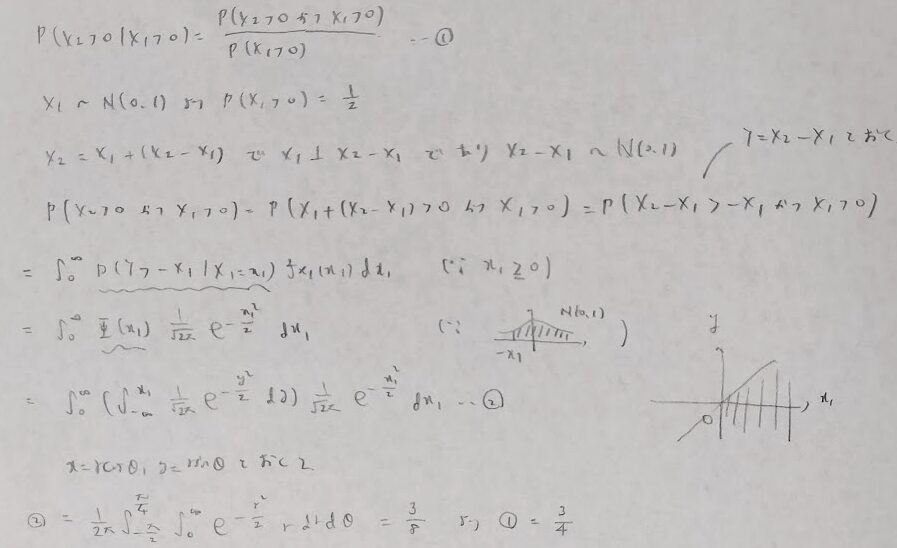
平成20年度問1(11)増分性

平成22年度問1(11)重積分

平成28年度問1(10)変化球

2018年度問1(10)積率

2021年度問1(11)階段型

平成18年度問1(11)標準正規分布

平成25年度問1(12)指数分布
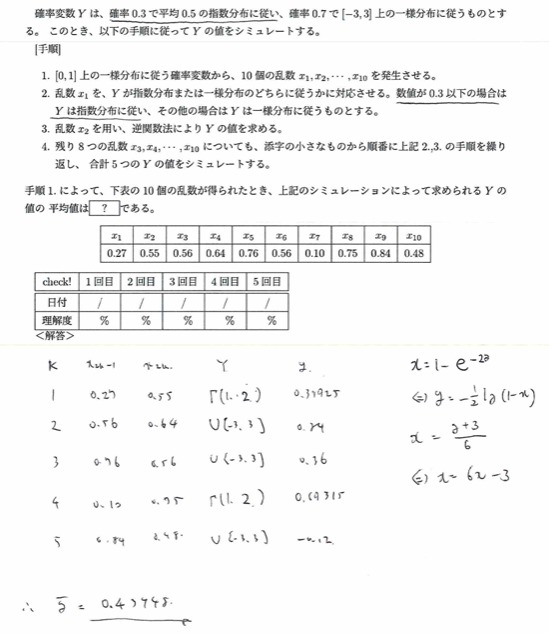
平成29年度問1(12)遊園地

2021年度問1(12)ポアソン分布

平成19年度問1(12)繰り返し回数を最小にする定数c

平成21年度問1(12)絶対値Xの値

2024年度問3(3)棄却法

2019年度問1(12)変化球

平成20年度問1(12)指数分布

2018年度問1(12)幾何分布

平成22年度問1(12)負の相関法

平成27年度問1(12)負の相関法

2020年度問1(12)負の相関法

平成28年度問1(12)制御変量法

アクチュアリー数学で必要な公式を過去問をベースに総整理しましたがいかがでしたでしょうか。なお公式は『アクチュアリー試験 合格へのストラテジー 数学 第2版』を元にしております。本書はアクチュアリー数学受験のバイブルで受験者は必携の書です。
試験直前に見直して合格を目指しましょう!