統計検定1級でも頻出の点推定に関する問題をアクチュアリー数学の過去問を用いて解説していきます。他分野と比較すると比較的難易度は低目の章になりますが、手強い問題もあります。頻出分野のため過去問数が多くなっていますので区間推定よりも難易度が高い問題が混じっています。。本試験ではしっかりと得点できるように訓練していきましょう。
全体的なおすすめの公式集は『アクチュアリー試験 合格へのストラテジー 数学 第2版』です。お手元に置いて本記事をご覧くだされば学習効率が上がります。
モーメント推定量の過去問題は、それぞれの確率分布の期待値と分散の公式を覚えていれば、あとは標本平均と標本分散との比較ですべて解けます。その意味でも『アクチュアリー試験 合格へのストラテジー 数学 第2版』の公式は試験までにしっかり覚えておくべきです。
最尤推定量
平成元年度問1(4)一様分布

有名な結果になります。アクチュアリー数学では覚えてしまってOKです。
平成元年度問2:指数分布

こちらも有名な結果になりますので覚えましょう。
2024年度問2(1)指数分布

平成3年度問1(2)最小統計量

終盤が難しいですが、条件式を見れば答えまですぐです。
尤度を大きくすることを原則に考えましょう!
平成4年度問1(1)幾何分布

この問題は問題文から瞬時に答えを出したいですね。幾何分布であることに気づくことが第一です。すると下記の本に載っている公式がすぐに使えます。もしもファーストサクセス分布の場合は、期待値はpの逆数であることを用いてモーメント法を用いて、pの推定値はxの平均値の逆数になります。幾何分布とファーストサクセス分布の関係を考えて、結果が上記になることが感覚的に判明します。
平成5年度問1(4)尤度設定

尤度の設定を自分で行います。nの範囲が盲点ですのでご注意ください。
平成6年度問1(3)幾何分布

通常の池の問題とは設定が異なりますので、しっかりと問題文を読みましょう!
平成7年度問1(4)二項母集団

そんなに簡単ではないので計算はしっかりと行いたいところです。しかし実際は「標本平均を母平均に等しいと見なす」ことが、最尤推定の目的である「観測データを最も確からしくする」ことと一致することを用いて考えることもできます。
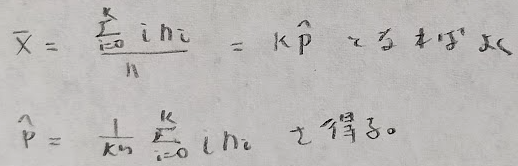
平成9年度問4:推測可能なタイプ

本問はカイ2乗分布の知識があれば迅速に処理できます。
平成11年度問1(4)信頼度

信頼度の定義は覚えておくべきです。
平成11年度問2:回帰分析

統計検定やQC検定などでの典型パターンの結果になる問題です。結論を予想しつつ誘導に乗れるようにしておきましょう。
平成12年度問2(6)標準正規分布
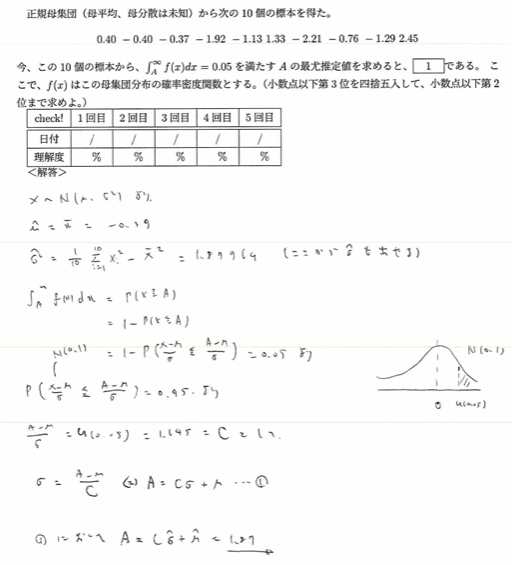
かなりの良問です。最尤推定量をどんどん代入していきましょう。
平成13年度問2(7)定義に沿って考える

平成13年度問4:負の二項定理

負の二項定理がとても覚えにくいと思ったので、一般化二項定理の特殊な場合としての負の二項定理を導きました。ご覧ください。

平成15年度問2(4)二項母集団
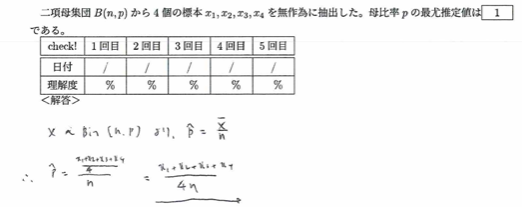
この結果のnに1を代入したものがよく知られている公式です。母比率の意味と、式の意味を考えても納得のいく結果です。
平成16年度問2(5)一様分布

尤度を最大にすることだけを考えましょう。本問は頻出問題になりつつあります。
本問は混乱する要素が多いのでポイントを解説しますと、確率密度関数を一様分布の和のイメージで設定します。そして分母に注目して、どの文字について考えていくかを考察し、表にまとめます。
平成18年度問1(6)二項母集団
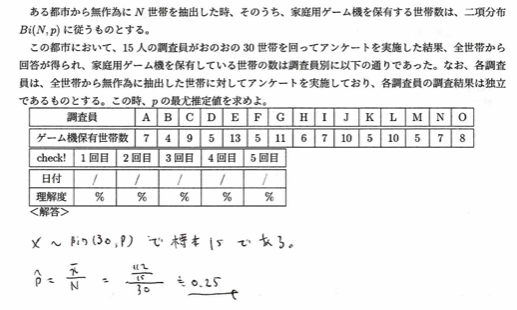
何がNかを見落とさないようにしましょう。基本的な問題です。イメージ的には1人1人の調査団が30世帯を訪れて得た結果(0から30までの値)の平均が各家庭の所有するゲーム機の数です。それを30で割ることにより母比率の最尤推定値が求まる感じです。
平成27年度問1(5)変化球

5回中2回が当たりで、あとは引く順番を考える反復試行の確率の応用問題です。
2019年度問1(5)池の魚の問題

二項分布と超幾何分布の違いについての問題です。モーメント推定量との融合問題になっています。
2021年度問1(6)最尤推定量最難関
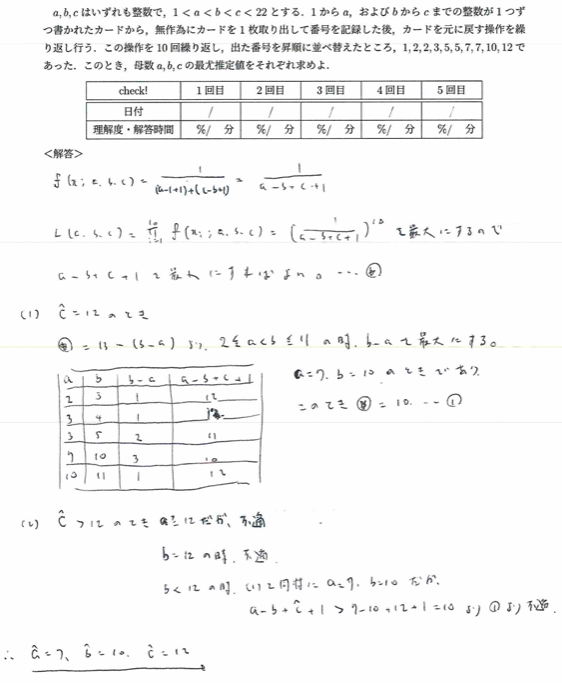
今のアクチュアリー数学では穴埋め式なので、1つ1つしらみつぶしで探して行った方が早いかも知れません。
不偏推定量
昭和63年度問2:中央値

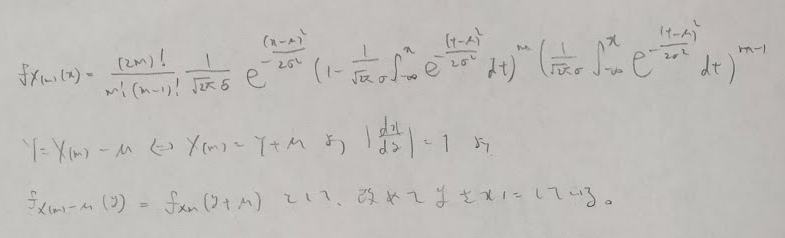
積分の部分が誘導なしではきついですね。今のアクチュアリー数学では、問題文の主張を覚えて、誘導に乗る作戦で行きましょう。
平成4年度問1(5)一様分布

ベータ分布の関係式を用いるために標準一様分布に変形する箇所が山場です。パッと思いつけるように訓練しておきましょう。
平成5年度問1(1)標準正規分布の絶対値の高次モーメント

どのような変形でも答えに辿り着けます。定数部分をどんどん置き換えていくのが最もスピーディーです。最後は解答のように公式を使う形になります。
平成6年度問2:ガンマ分布の高次モーメント

THEアクチュアリー数学という感じの問題ですね。2025年11月現在の試験の難易度だとこれが小問集合の序盤に来ます。
平成14年度問2(4)不偏推定値

不偏推定値を聞いてくる珍しいタイプの問題でかなりの良問で今後の出題可能性は高いです。
平成19年度問1(8)一様分布

これまでの総合的な知識が要求される問題です。しかしアクチュアリー数学では基本問題として解きたいところです。要するに2025年11月現在のレベルの試験では小問集合の序盤に登場してもおかしくない問題です。
有効推定量
平成4年度問2:コーシーシュワルツの不等式

平成8年度問1(2)比例式

足して1に気付けるかが難しいですが、公式化したい問題です。
平成8年度問3:ラオブラックウェルの定理関連(点推定最難関)

十分統計量で条件づけた不偏推定量の期待値は有効推定量であることの証明ですが、難しいです。試験では条件付けても不偏性があり、新しい推定量の方が有効であるということを思い出して結果を選べば良いですが無味乾燥ですよね…。
平成9年度問3:平方完成

共分散の存在に気を配りましょう。
平成11年度問1(6)一様分布

どうしてもXが一様分布に従うことが腑に落ちないので証明してみました。近似を用いています。

結局は、全て等確率で起こるというイメージに従うことが本質なのですが直感的にも納得がいく結果だと思われます。
Xが一様分布に従うことに気づけるか?がポイントです。イメージとしては適当な数を考えたときに、それを(例えば)3で割った時の余りは0と1と2があり、それは一様分布に従っていることの一般化(3で割ることを3.14で割るなど)です。
よくこんな面白い問題が作れるなぁと感心します。アクチュアリー数学は難関ですが、良問が多いのが特徴です。
平成11年度問4:有限母集団

(2)が核です。有限母集団の公式を駆使して解き切りましょう!
(2)を一般化させた問題は統計検定1級でも出題されそうな問題となります。
平成16年度問2(1)平方完成

有効推定量を考えているので、前提条件として不偏性を満たさなければなりません。
平成17年度問2:最大統計量

最大統計量を求める必要があるので、分布関数を考えます。ここの計算が大変なので難易度が高くなっています。
十分推定量(充足推定量)
昭和62年度問1:二項母集団

問題2は時間がないときはモーメント法を用いて答えを予想しましょう。序盤はテクニカルなので注意です。
平成10年度問1(6)ガンマ分布

不偏推定量でなければ推定量は有効性を持ちません。
平成23年度問3:総合問題


あるsについて〜のところ(⑩の穴のところ)が分かりにくいですが、最後のあたりは大事なエッセンスが詰まっています。
全体的に難易度順でまとめると、アクチュアリー数学ではモーメント推定量<不偏推定量<最尤推定量<有効推定量<十分推定量の意見です。モーメント推定量は公式を知っているか?で解答時間に差が生まれますので、しっかりと公式を暗記しておきたいところです。
全体的なおすすめの公式集は『アクチュアリー試験 合格へのストラテジー 数学 第2版』です。お手元に置いて本記事をご覧くだされば学習効率が上がります。
モーメント推定量の過去問題は、それぞれの確率分布の期待値と分散の公式を覚えていれば、あとは標本平均と標本分散との比較ですべて解けます。その意味でも『アクチュアリー試験 合格へのストラテジー 数学 第2版』の公式は試験までにしっかり覚えておくべきです。




