アクチュアリー数学のシミュレーションの過去問を解説します。本章はモデリングの最終章であり、アクチュアリー数学の最終章でもあります。内容は逆関数法・棄却法・合成法・分散減少法の4つです。順に解説していきます。分散減少法では負の相関法と制御編療法を扱います。
全体的なおすすめの公式・問題集は『アクチュアリー試験 合格へのストラテジー 数学 第2版』です。お手元に置いて本記事をご覧くだされば学習効率が上がります。
逆関数法
確率変数が連続型か離散型かでXの作成方法が異なります。離散型の方が難易度が高いです。

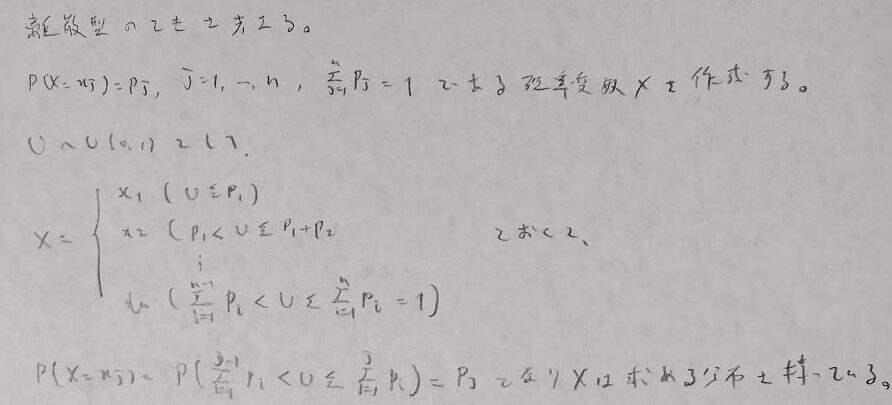
平成17年度問1(8)標準正規分布

逆関数法の最難関の難問です。とにかく意味を見出しづらい問題です。
平成18年度問1(11)標準正規分布

問われている内容は前年度とあまり変わりません。問題文で聞かれている内容把握が最も大切です。
平成25年度問1(12)指数分布
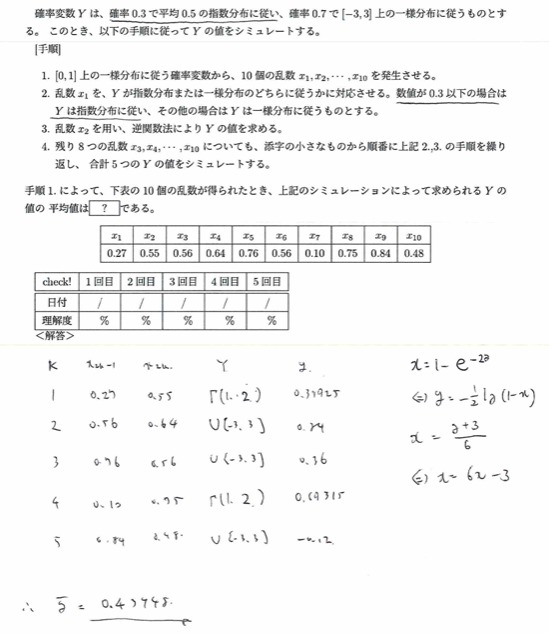
平成29年度問1(12)遊園地

2021年度問1(12)ポアソン分布

本問は逆関数法の良問です。中盤の穴埋めができたか?で勝負が決まります。
総じて逆関数法は問題文を読んで適切な立式ができるか?が問われています。
棄却法
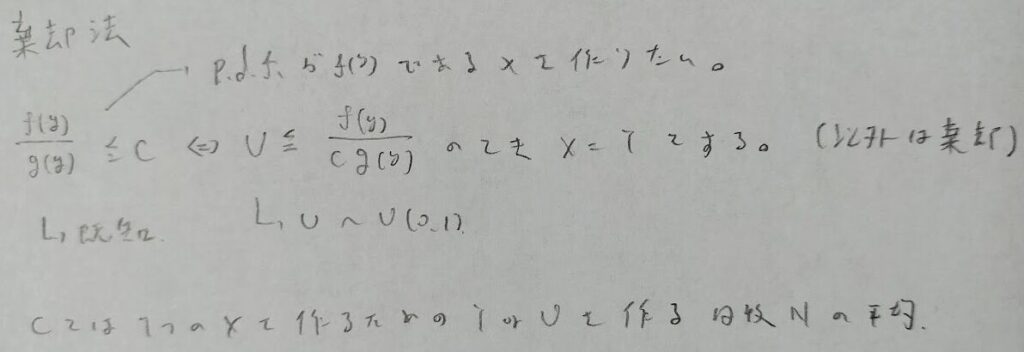
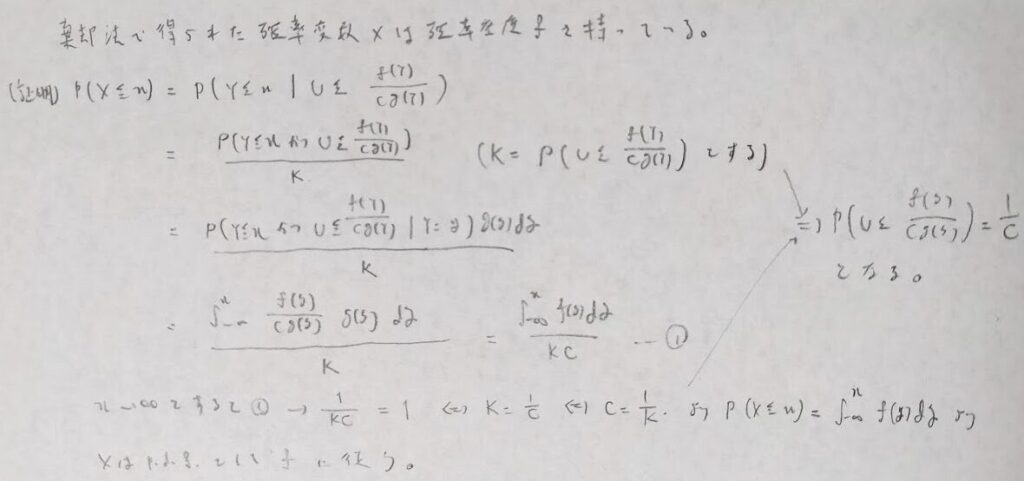
平成19年度問1(12)繰り返し回数を最小にする定数c

平成21年度問1(12)絶対値Xの値

本問を通して棄却法のやり方をおさえましょう。
2024年度問3(3)棄却法

2019年度問1(12)変化球

2022年度問3:ボックス・マーラー法と極座標法


棄却法で最も難しいのがボックス・マーラー法と極座標法です。しっかりと練習しておきたいですね。
合成法

合成法では係数が小さい順であるかを確認し、分布関数を用いることにも注意しましょう。
平成20年度問1(12)指数分布

係数和が1であることに注意しましょう。
2018年度問1(12)幾何分布

本問はかなりの難問です。落ち着いて取り組みたいですね。
分散減少法

負の相関法と制御変量法の概要を解説した後で過去問に入ります。
負の相関法と制御変量法の解説
負の相関法
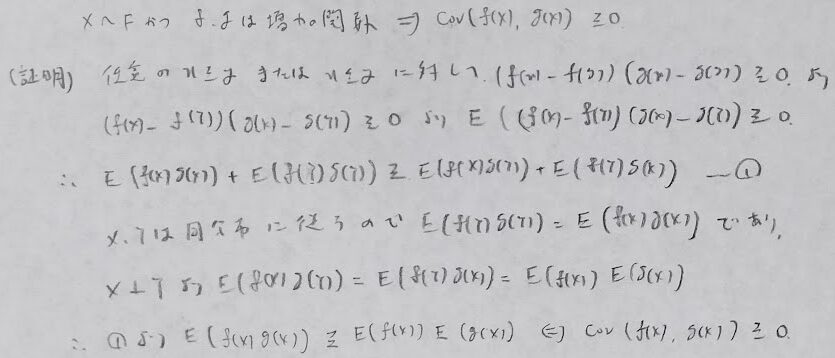
これを用いると負の相関法の根本的な部分を証明できます。
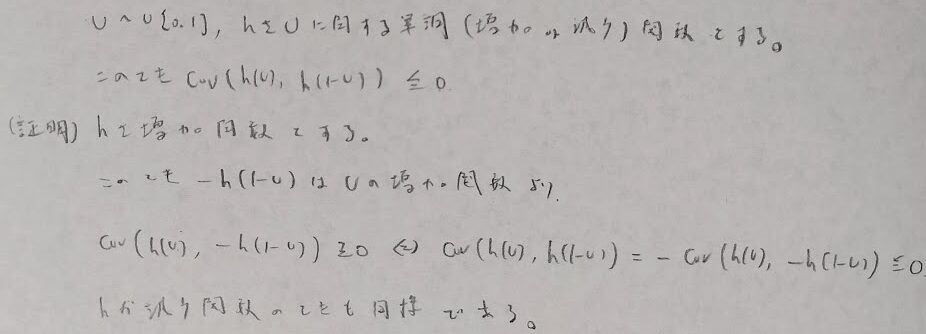
この結果を用いると分散を小さくするために下記の不偏推定量の分散は小さくなります。
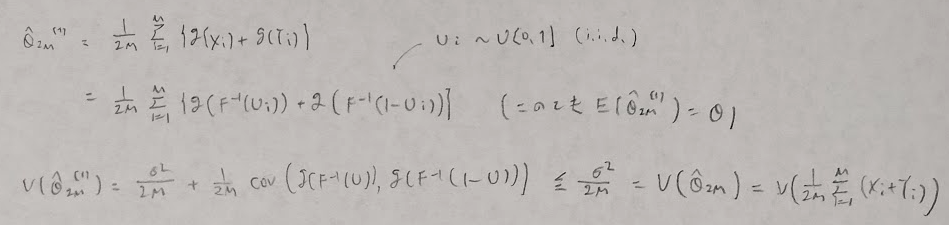
ここでFが標準正規分布の時は上の結果がさらに簡略化します。
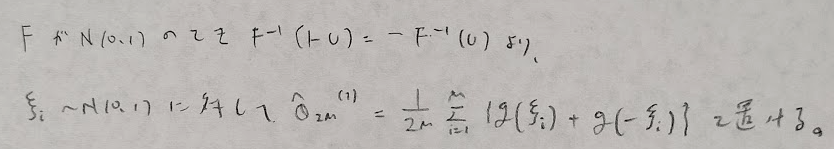
制御変量法
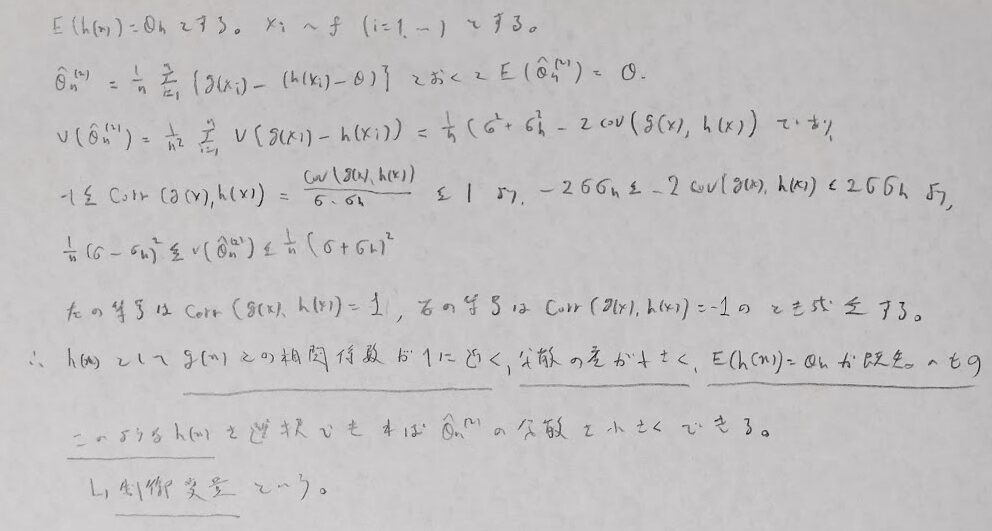
制御変量を構成します。

制御変量と回帰分析の間には関連性があります。
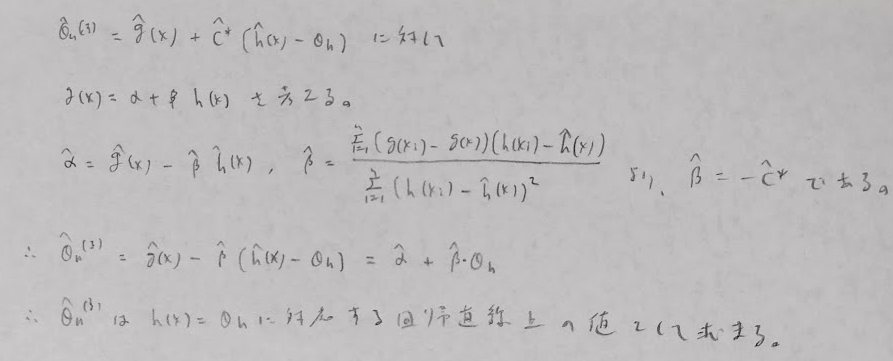
平成22年度問1(12)負の相関法

この問題は典型問題です。しっかりと解き切りましょう!
平成27年度問1(12)負の相関法

2020年度問1(12)負の相関法

平成28年度問1(12)制御変量法

制御変量法の公式を知っているのか?の問題です。計算もしっかりと行いましょう!
制御変量法では分散の結果から信頼区間を求めることができます。
乱数の作成方法
過去問には載っていませんが指定教材に掲載されている乱数生成の方法についてまとめておきます。離散分布の場合の方が難易度が高いです。ガウス記号(int関数)を多用するためです。
一様乱数
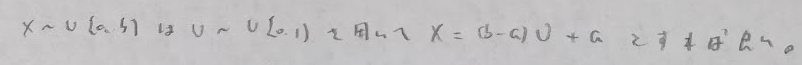

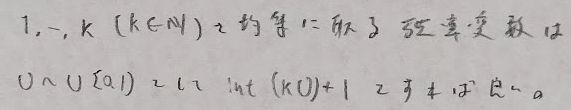

指数乱数
パラメータ1に従う指数分布を挟むことがポイントです。

ガンマ乱数
上の指数分布を組み合わせるだけです。

ただしこの方法では大量の一様乱数が必要になります。
カイ2乗乱数

一様乱数が多いので、この量を半分程度にするために指数分布を利用することを考えます。

正規乱数
まずはCLT(中心極限定理)の利用がありますが、これは粗くなります。ただし実用性は高いです。
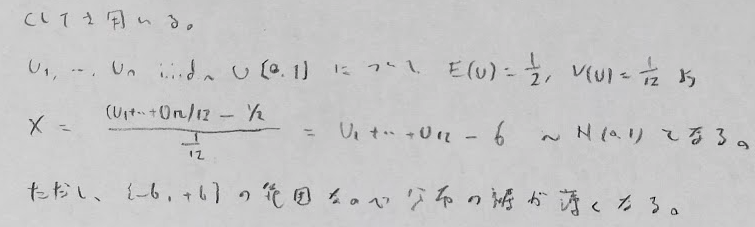
棄却法を用いることにより回数を減らせます。

(再掲)2022年度問3:ボックス・マーラー法と極座標法


二変量正規乱数
アクチュアリーの公式書の中に言及はありませんが十分に試験範囲として機能しそうなため掲載します。下記に作成方法を掲載していますが、前提条件として2つの独立な標準一様乱数を作成しておきます。
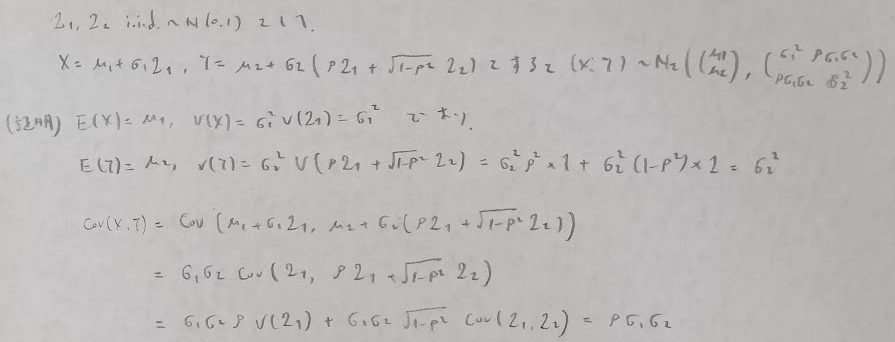
ベータ乱数
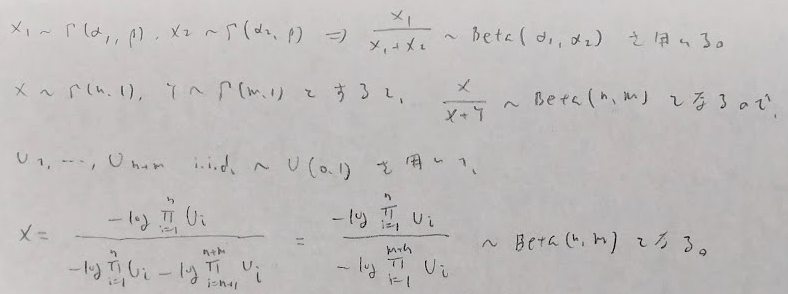
幾何乱数
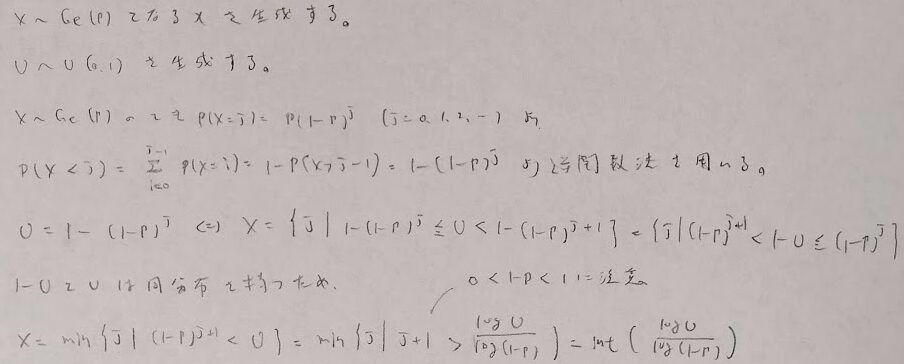
二項乱数
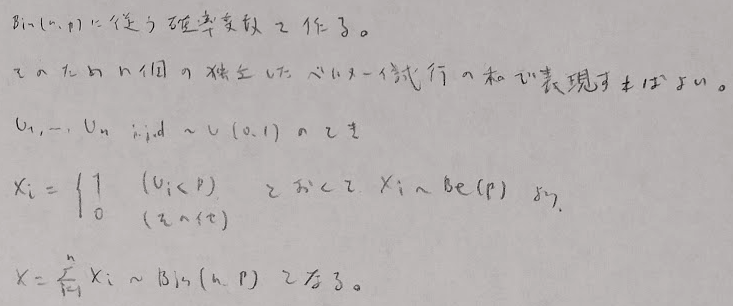
負の二項乱数
まず最も単純な方法は幾何乱数の和として表現することです。
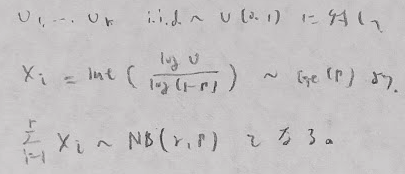
次にガンマ分布とポアソン分布との混合分布として表現する方法がありますので、命題を証明しておきます。
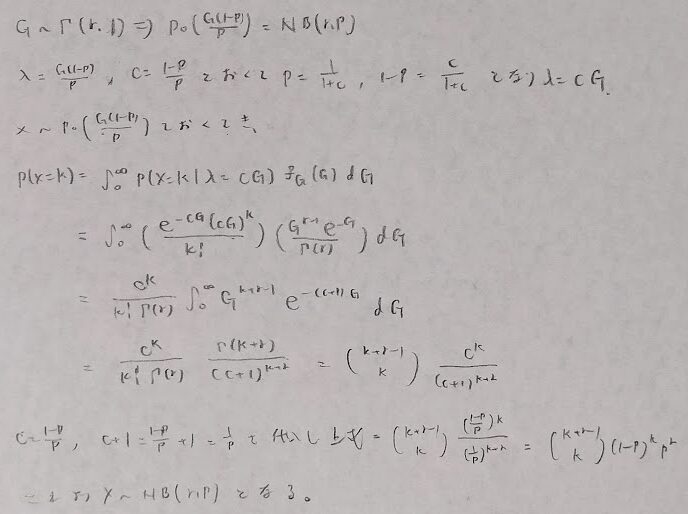
しかしこのためにはポアソン乱数の作成ができないといけないため、最後にポアソン乱数の生成方法を学習します。
ポアソン乱数

なぜ直前か?というと超えてしまった場合はパラメータそのものが変化してしまうからです。
全体的なおすすめの公式・問題集は『アクチュアリー試験 合格へのストラテジー 数学 第2版』です。お手元に置いて本記事をご覧くだされば学習効率が上がります。




