統計検定1級の対策書として公式本以外で真っ先に買うべき本である『データ解析のための数理統計入門』の第11章の解説と演習問題を自力で解いた学習の軌跡の記事です。本章は重回帰分析に関する理論の展開となります。本記事の内容が本書において最も行間が広い分野だそうです。自分も解いていて苦戦した箇所がありましたが、多くの方が似たような状況のようです。
本記事がその方々の助けになれば幸いです。
本章で重回帰モデルからガウス・マルコフの定理までを前半としてスピーディーに解説します。後半はコクランの定理などテクニック面が強い印象があります。1度で吸収しようとせず、ゆっくりと何回も本記事をお読みになって共に頑張っていきましょう!
統計検定1級青本の第12章の説明と例題
本記事はガウス・マルコフの定理より先の内容が難易度が高くなっています。ガウス・マルコフの箇所を前半としたのはアクチュアリー数学での重回帰分析の区切りの部分であるためです。要するに後半は統計検定1級に相当するハイレベルの内容となっております。
重回帰モデルの行列表示からガウス・マルコフの定理まで
本書『データ解析のための数理統計入門』ではより実践的にそして理論的に重回帰分析を理解するために、射影行列Pの導入がなされています。本記事を通して要するに冪等行列とは何か?その使い方についても共に慣れていきましょう!

偏回帰係数に切片(定数項)は含まれません。しかしβのことを慣例上、偏回帰係数ベクトルと呼びます。
本書ではβの最小2乗統計量に当たりをつけて、それが残差平方和を最小にすること、そしてその根拠に射影行列Pを導入することによって証明しています。証明の途中で冪等行列の考察が重要になってきます。

残差平方和が表す幾何的な意味を考えます。直交射影行列Pが大活躍します。Pの2乗がPと等しい行列は射影行列であることの必要十分条件です。一度射影したものをもう一度射影しても変わらないことから冪等性が成り立つわけです。

僕は何冊か数理統計の本を読んできましたが、ここの部分の説明について本書『データ解析のための数理統計入門』が最もわかりやすくかったです。
期待値ベクトルと(分散)共分散行列を定義し性質を確認します。最後の性質は2次形式の期待値の重要な性質でトレースが出てくることが特徴です。また後ほど登場しますが2次形式とコクランの定理も相性最高です。
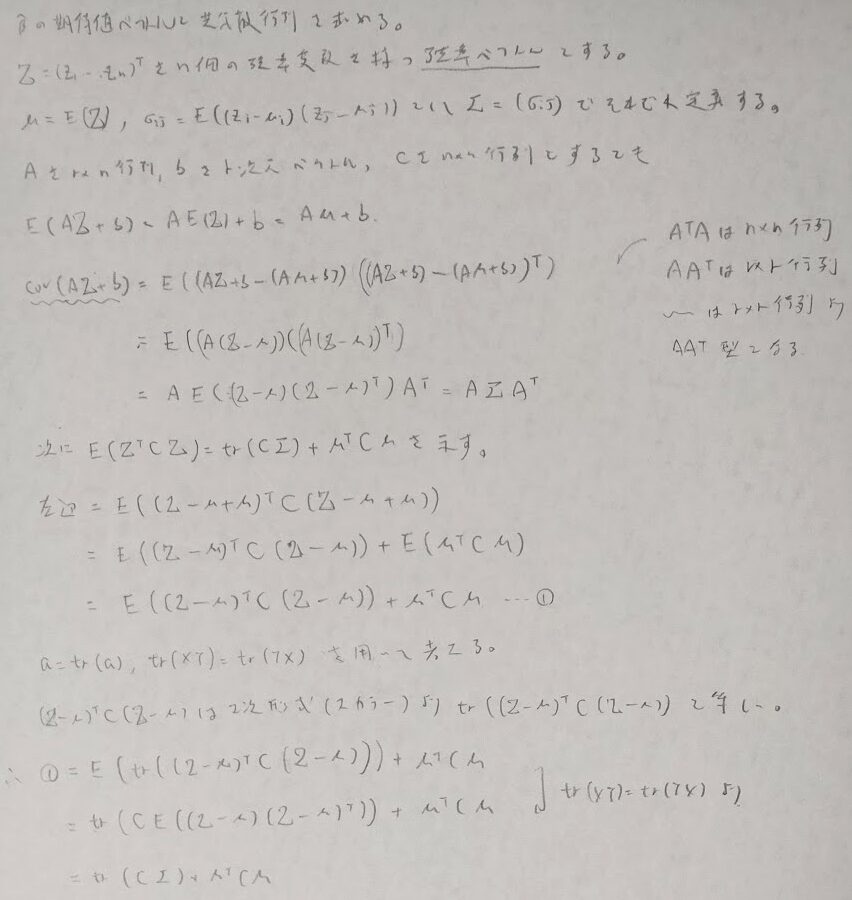
2次形式の期待値の重要性質を用いて、βの最小2乗統計量の性質や誤差分散の不偏推定量を結果を導きます。単回帰分析の記事で出てきた内容が重回帰分析の中で証明されたわけです。

いよいよガウス・マルコフの定理です。ここでも上で用いた誤差の期待値が0ベクトルになるなどの性質は保存されたまま用います。
まだこの段階では正規性の仮定は加わっていないことに注意です。

誤差項に正規性を仮定する場合
次は誤差項に正規性を仮定する場合になります。どんどん仮定がキツくなっていることに注目しましょう。ただしここの部分の証明の理解が難しくかなり苦戦しました。
ここの部分、結構苦戦されている方が多いみたいでtweetした内容が反響あるみたいです。

コクランの定理
コクランの定理を用いると見通しが良くなります。
コクランの定理は多変量の正規分布と相性が良さそうです。またいろんなバージョンがあり、『データ解析のための数理統計入門』で解説している内容は最も一般的な場合のようです。準備段階として以下のTweetにて冪等行列においてトレースが出てくる根拠の周辺について解説しています。

重要な箇所は多変量正規分布に従っている確率変数の2乗(に相当する部分)が左辺にきて、右辺が2次形式(対称性の仮定)で表せたとして、その表現行列のランク(を出す際にトレースを用いるため冪等性の仮定が必要)の和が多変量正規分布の次元に等しいことが言えれば、独立性とカイ2乗分布の自由度が一気に確定してしまう強力な定理となります。
コクランの定理を用いると先ほどの内容がシンプルに表現されます。後に解説しますが、コクランの定理を使用するには2次形式の形に持っていくこと→注目する行列が対称であり、冪等であることが要求されます。
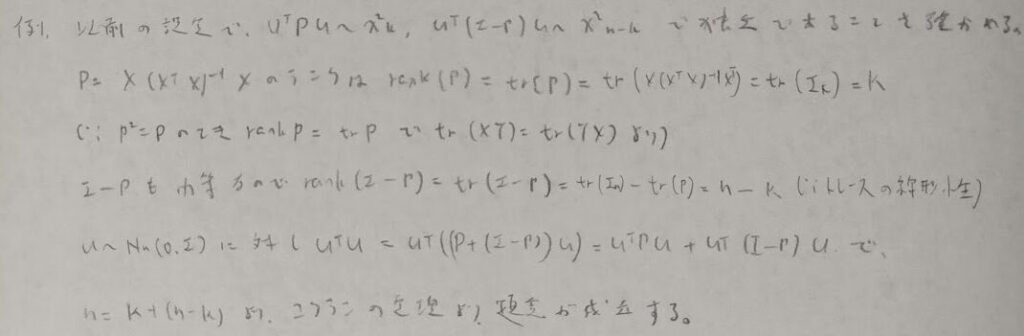
ランクといえばその際に成立する内容と、フルランクでない場合に生じる弊害も紹介しておきますね。

回帰係数の仮説検定
統計検定やQC検定にも登場する頻度の高い仮説検定との絡みに入ります。ここでは有意水準αの検定にピッタリはならないものの近似でも良いのでとにかく検定を求めたい!という時のための尤度比検定、そして有意水準αにピッタリとなる検定(今回はF検定とt検定)の2種類をこの順で導出します。尤度比検定では汎用性の高いバージョンで紹介します。
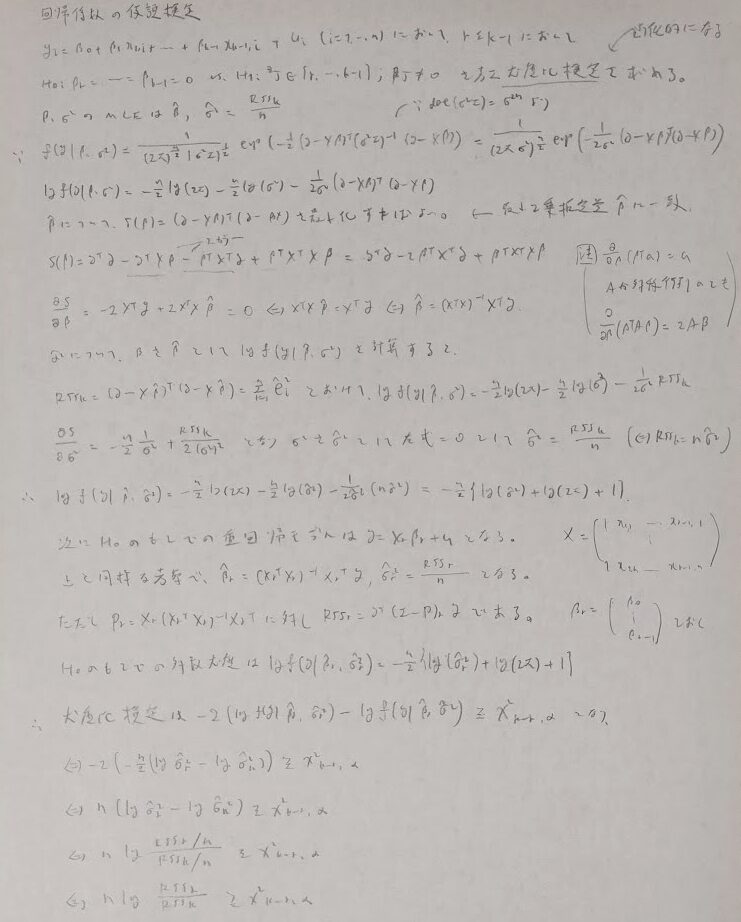
しかしこの検定ではあくまでも近似で得られる検定なので、近似を用いない検定を導出します。

次に特定の回帰係数の成分に関する検定について考えます。こちらはt検定になります。こちらは回帰係数の推定量の周辺の対角成分がポイントになります。

重回帰分析では変数選択が大事になります。そのため決定係数関連の話題を整理します。決定係数は重相関係数の2乗になります。
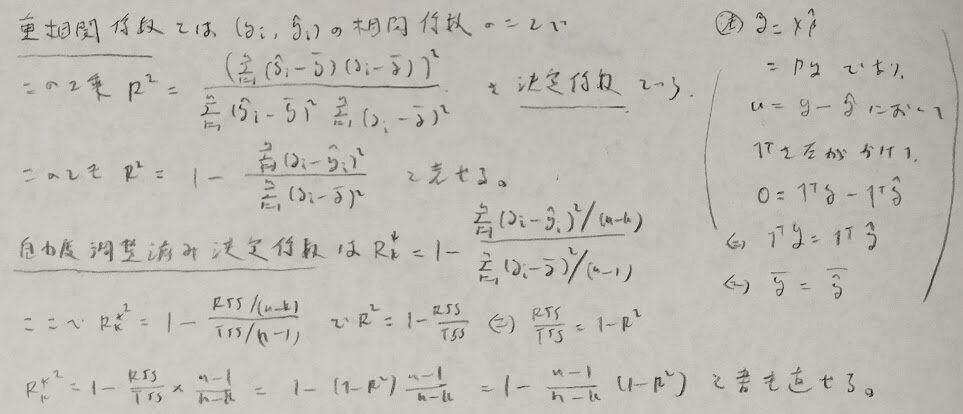
最後の式はかなりの盲点です。気をつけましょう。
次に予測誤差を小さくするための方法を考えます。カルバック・ライブラー情報量で測ります。またそれを用いた際の期待予測誤差を考えます。統計モデルに依存する部分の漸近的な不偏推定量が赤池情報量規準(AIC)となります。結局対数尤度を中心に計算していることになります。

またAICは変数選択における尤度比検定と類似点があります。どちらが評価が甘いかは右辺の値で判断できます。
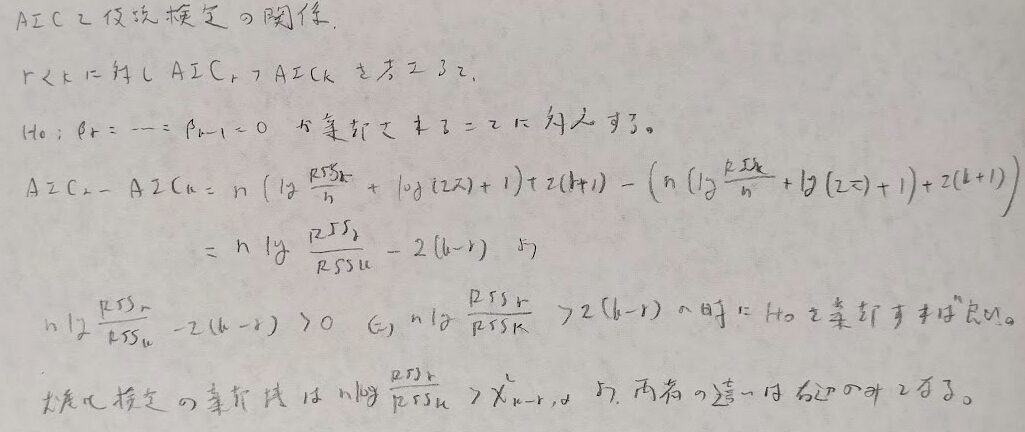
AICは分布を仮定して議論を展開しました。分布が用意できない場合はクロスバリデーションを用いて直接予測誤差を推定します。
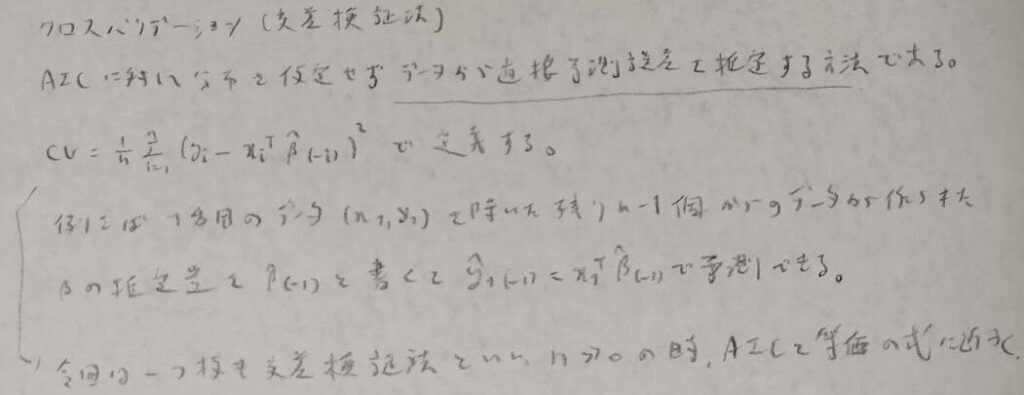
最後に重回帰分析モデルの応用として多項式モデルと双曲線モデルを紹介します。それぞれを用いた場合の方がモデルのデータへの当てはまりの良さが向上する場合があります。

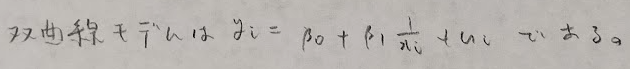
またダミー変数を取り入れた解析ではAICが小さくなる場合があります。
統計検定1級青本の第12章の演習問題
問1:多項式回帰
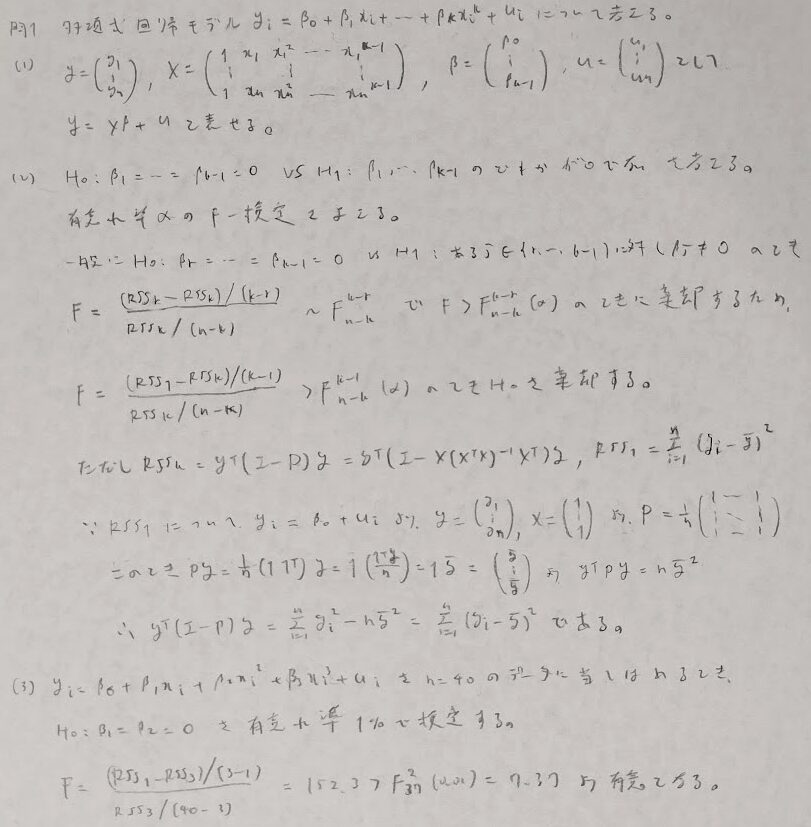
F統計量は残差平方和を意識すると覚えやすいです。
問2:t検定の問題
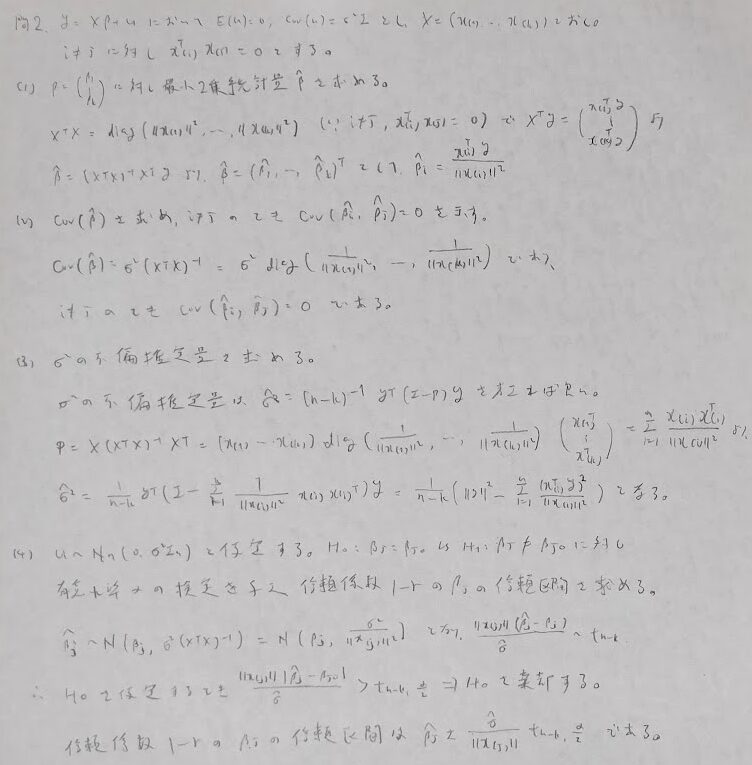
問3:共分散行列の定義
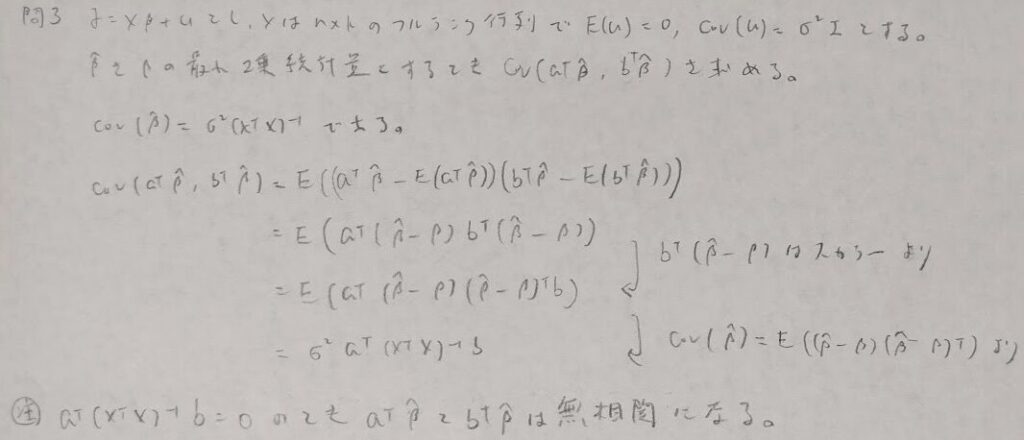
問4:コクランの定理
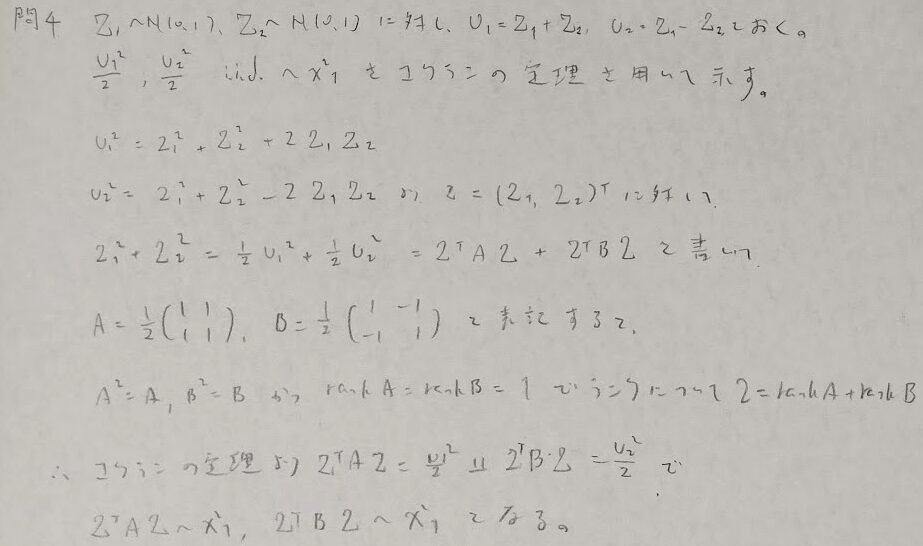
コクランの定理を最後に使っていますが、左辺の2とは、2つの確率変数Z_1とZ_2が2変量標準正規分布に従っていることの2です。対称行列の確認が抜け落ちているように感じますが、それは2次形式で表現できていることから自明と見做します。
本記事で何度も登場するトレースの値は対角化前後で不変です。その理由はトレースの中身の行列には交換が許されるからです。
以上で重回帰モデルの内容を終了します。QC検定1級などまた別の角度から問われる内容もありますが、本記事で多くの典型的な問題パターンは網羅できているはずです。他にも下記に別の視点から考察した重回帰分析の記事を載せます。本記事は『データ解析のための数理統計入門』を軸に書きました。本記事ををお読みくださり、ありがとうございました。