統計検定1級の新たなバイブルとして青本という名前で親しまれている久保川先生の『データ解析のための数理統計入門』を第1章から自力で解いていき、皆様と共に注意すべき箇所などをまとめた記事になります。
∩∪⊂∈←よく使う集合記号を載せておきます。コピペなどにお使いください笑
本記事の例題や演習問題の問題文は下記の参考書をご参照ください。また答案は久保川先生の模範解答とは異なる解き方をしている問題もございます。ただし最終結果は合っておりますのでご了承ください。
確率モデルの章での注意すべき公式など
A∩(B∪C)=(A∩B)∪(A∩C)
A∪(B∩C)=(A∪B)∩(A∪C)
これはいわゆる分配法則ですが、数での分配法則と同じと考えてしまうと覚えにくいです。∩と∪について分配法則が成り立つと考えた方がスムーズで覚えられます。
確率の性質は以下の確率の定義から導くことができます。ポイントは上の公式を上手く下の3番目の式に適用することです。
A⊂Ω⇒P(A)≧0
P(Ω)=1
A1とA2が排反⇒P(A1∪A2)=P(A1)+P(A2)
二項係数の表し方を拡張すると多項係数も表現できます。
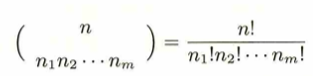
アクチュアリー数学でも出題される条件付き確率の一般化の公式は以下になります。
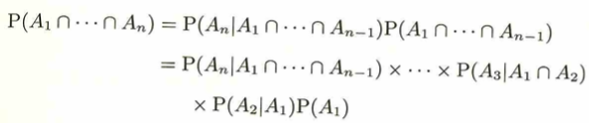
最後に事象の独立性の自然な一般化です。
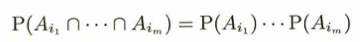
後述するペアワイズ独立との違いに注意しましょう。
例題
シンプソンのパラドックス
個々には確率が低くても合算すると確率が高くなる現象のことです。
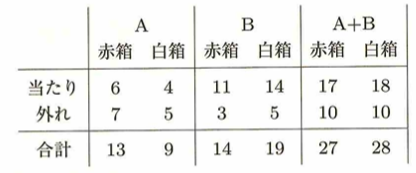
個々の箱AとBで考えると赤箱の方が当たる確率は高いですが、箱を合計すると当たる可能性が高いのは白箱の方になります。
誕生日問題
40人の教室の中で同じ誕生日の人がいる確率は次のようになります。
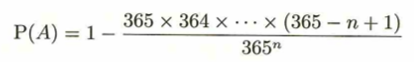
この式のnに40を代入して、0.89となります。
これ、かなりの多さに驚く問題ですよね!笑
多項係数を使う問題
statisticsの並べ方は10!/(1!1!2!3!3!)=50400です。
条件付き確率の問題(白玉と赤玉)
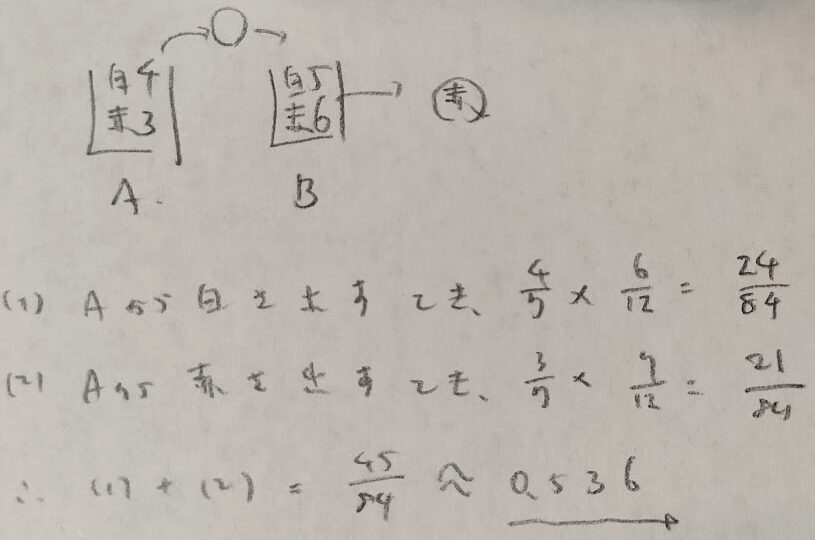
実際はこのように考えた方がスムーズに答えを出せます。模範解答はもっと難しく解いていました。
ウィルス検査
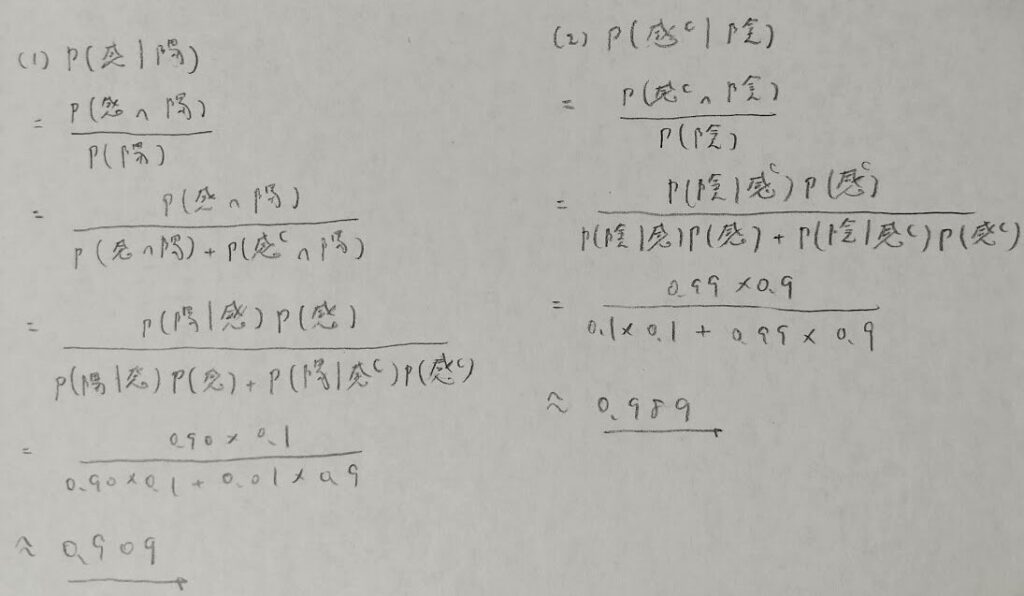
結果的には陰性反応の場合に感染していない確率の方が高く出ました。
ペアワイズ独立
例えば3つの事象があるときに、任意の2つは独立だが3つだと下式の最後の式が成立しない場合をペアワイズ独立といいます。
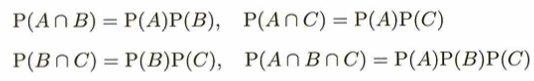
具体例としてはΩ={1,2,3,4},A={1,2},B={1,3},C={1,4}とするとき、最後の式のみが不成立になります。すなわち互いに独立⇒ペアワイズ独立ですが逆は偽です。
サイコロ
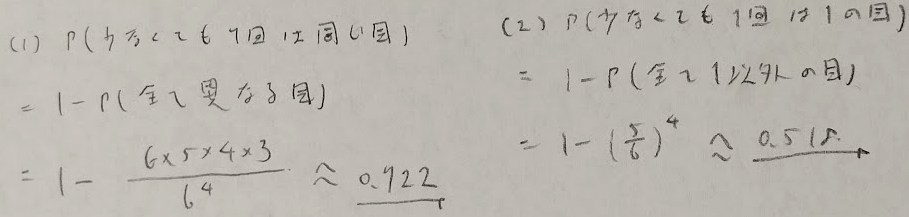
大学受験レベルの簡単目な問題でした。
演習問題
内定問題
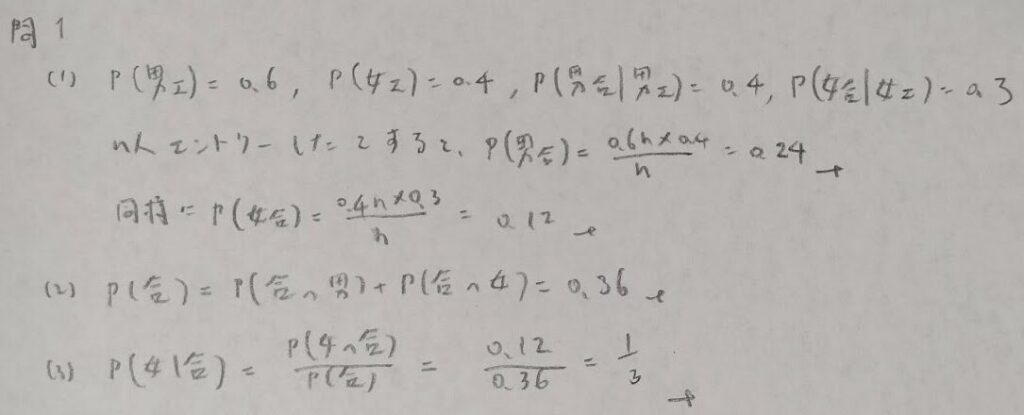
雨の問題
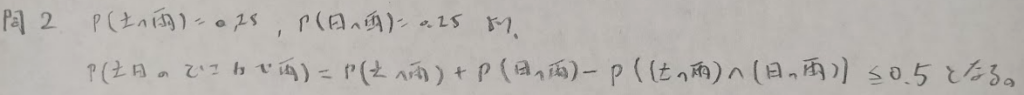
この問題、普通に0.5で合っていると思ったら間違っていましたね。良いひっかけ問題だと思います。
シンプソンのパラドックス

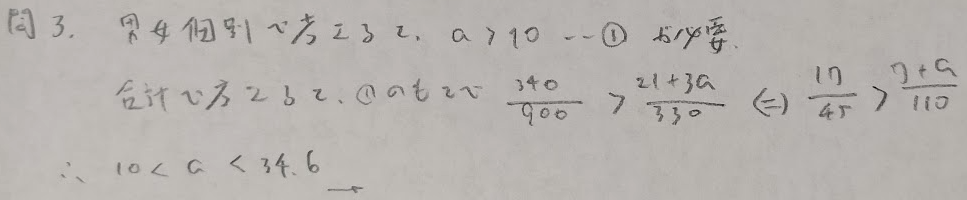
誕生日問題

4人だったら1%程度の確率ですが、意外と多いでしょうか?
事象の問題
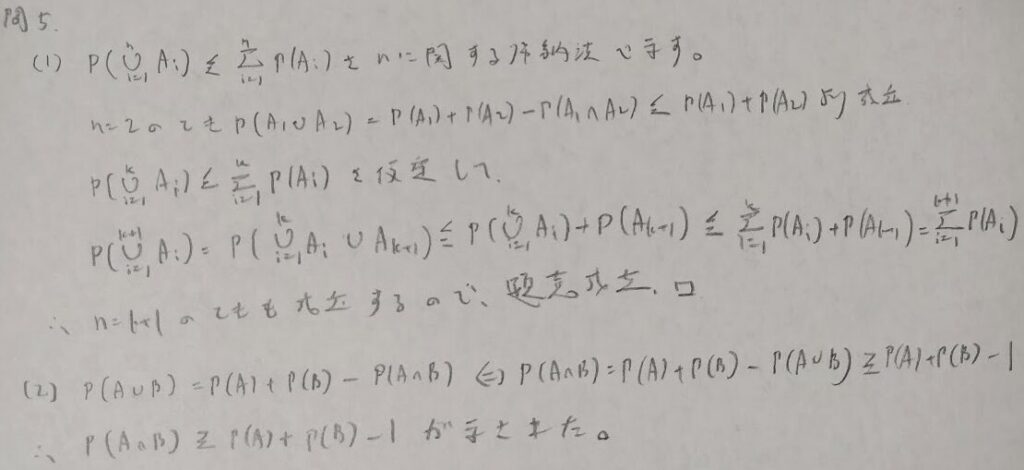
(1)の不等式はボンフェローニの不等式といいます。第15章の多重比較で再登場します。
不等式評価
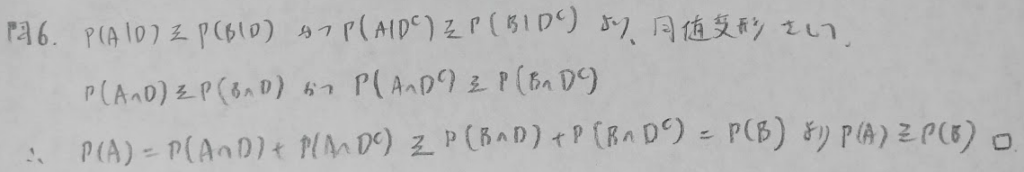
多項係数

条件付き確率
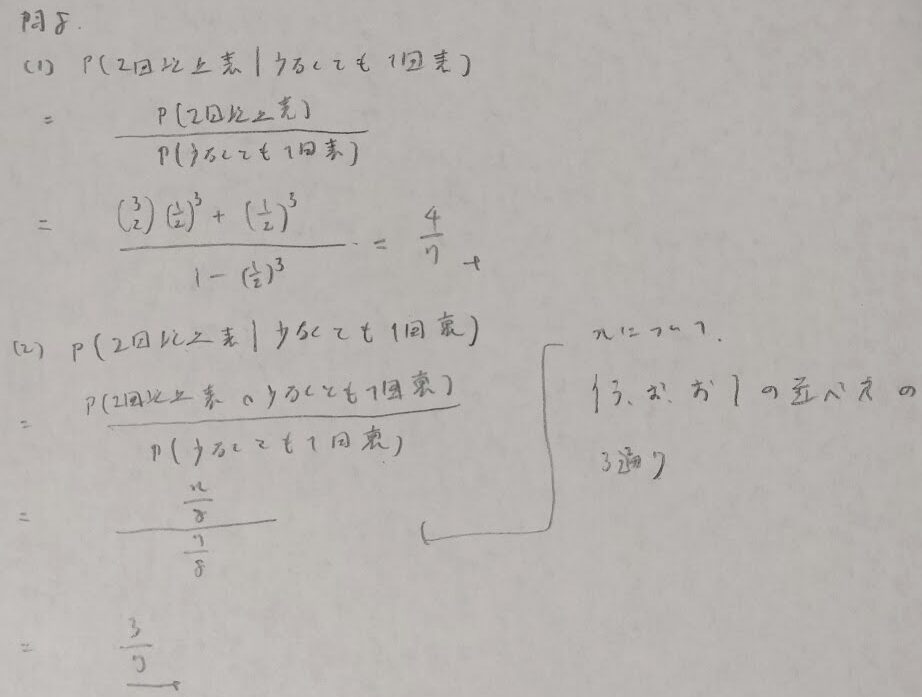
男女問題

事象の独立性判定

本問の類題がアクチュアリー数学で出題されました。
ウィルス検査(事前分布が一様分布)

ペアワイズ独立の例示

モンティ・ホール問題

どのように書けばよいか分かりませんでしたので模範解答を参照しました。なお、統計検定1級の共通問題で丁寧な誘導付きで出題されました。
二項定理の証明
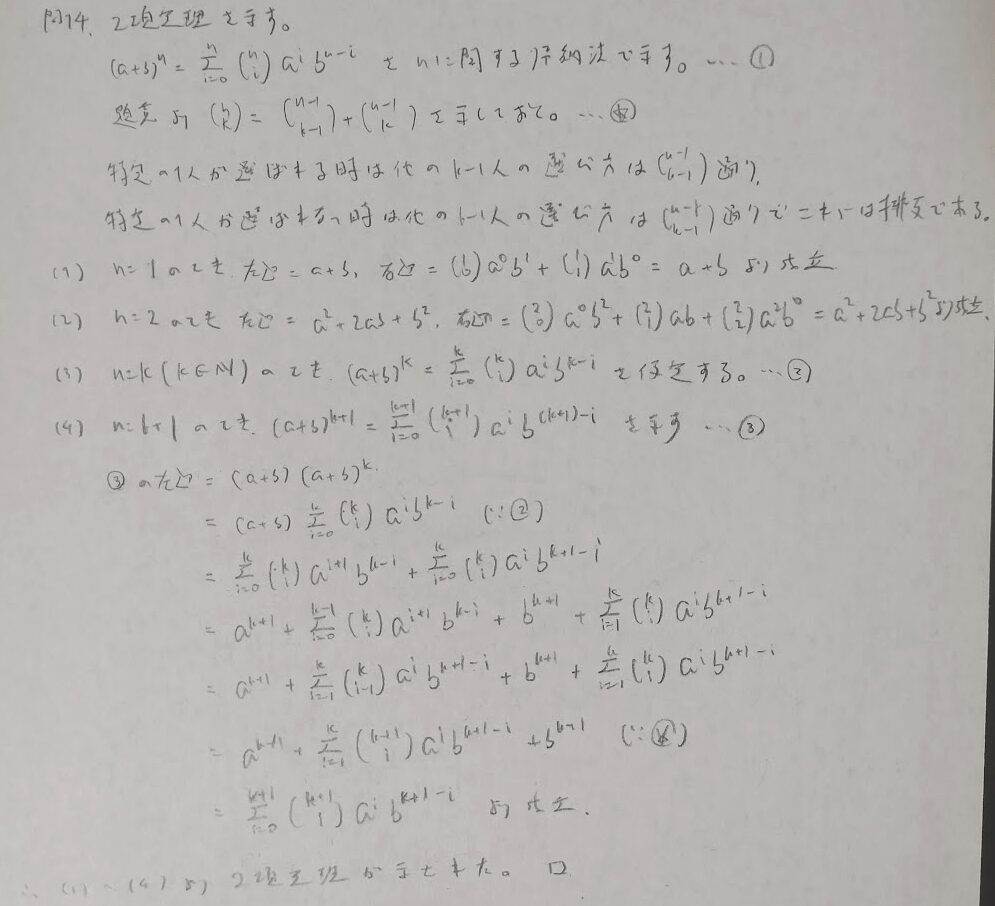
ラスボスは二項定理の証明でした。第1章から良問の続出で『データ解析のための数理統計入門』はアクチュアリー数学や統計検定1級のレベルに対応していると確信しました。本記事の詳しい問題内容などは下記参考書も併せてご参照ください。



