統計検定1級の対策書として公式本以外で真っ先に買うべき本である『データ解析のための数理統計入門』の第8章の解説と演習問題を自力で解いた学習の軌跡の記事です。本章は統計検定1級で頻出となる点推定に重点を置いた章で、理論と実践のバランスが素晴らしいことが特徴です。特に理論部分は流れるような解説が素晴らしく本記事においても参考にさせていただきました。
本章ではさまざまな推定量や推定法が登場します。その中でも特に重要なのは最尤推定量です。この推定量は他の推定量との関わりもあり、また次章の統計的検定や区間推定においても重要な役割を演じるからです。また後半部のクラメール・ラオの不等式にも登場するフィッシャー情報量も最尤推定量から派生している内容です。これらの理由から、本記事は最尤推定量の存在を意識した記事になりました。
統計検定1級青本の第8章の説明と例題
『データ解析のための数理統計入門』ではスカラー値とベクトル値は区別をして太字などで書かれています。また成分なども詳しく書かれています。しかし本記事では多次元への拡張を視覚的の類似点も伝えたいため、意味的に明らかにベクトル値であるときは成分表示を省略しています。

推定量にはさまざまな種類がありますが、直感的に理解しやすい一致推定量をまずは例にとります。一致推定量は確率収束で定義されます。また関連性があるのはモーメント推定量です。こちらも大数の法則が関連しています。モーメント推定量に適当な条件を加えた推定量は一致推定量になります。しかし『データ解析のための数理統計入門』ではその適当な条件の詳細は範囲外となります。

モーメント推定量と一致推定量の具体例を取り上げます。

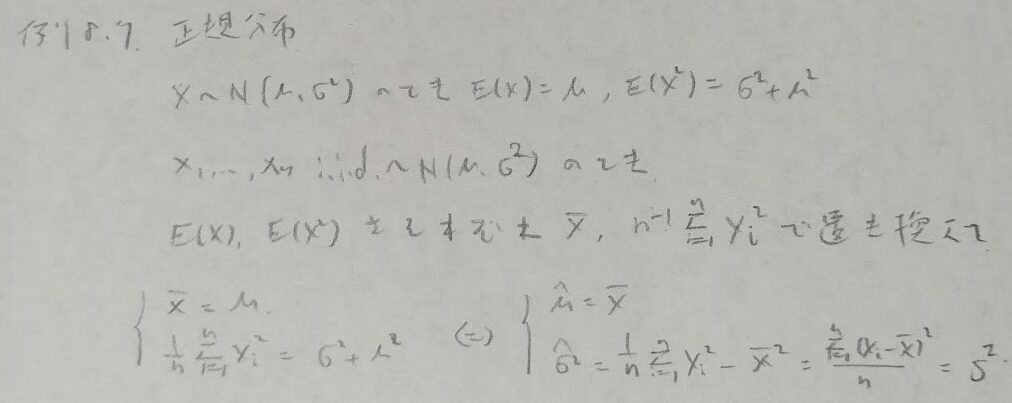
最尤法について進めます。こちらはサンプル数nを増やすと最尤推定量の分布は正規分布に収束する漸近正規性が成り立つため注目されている分布です。また最尤推定量は適当な条件のもとで一致推定量になります。さらに後ほど示しますが、最尤推定量→漸近有効です。またさらにラスボスであるラオ・ブラックウェルの定理における考えで用いることですが、最尤推定量→十分統計量の関数になります。
一致推定量は推定量の中で基本的な位置付けに感じますね。
そして最尤推定量はさまざまな推定量と関連があります。

対数尤度の計算において変数xは大文字Xで記述した方が後のために良いです。後のためとはフィッシャー情報量を求める際に期待値を考えるためです。
最尤法の具体例を列挙します。

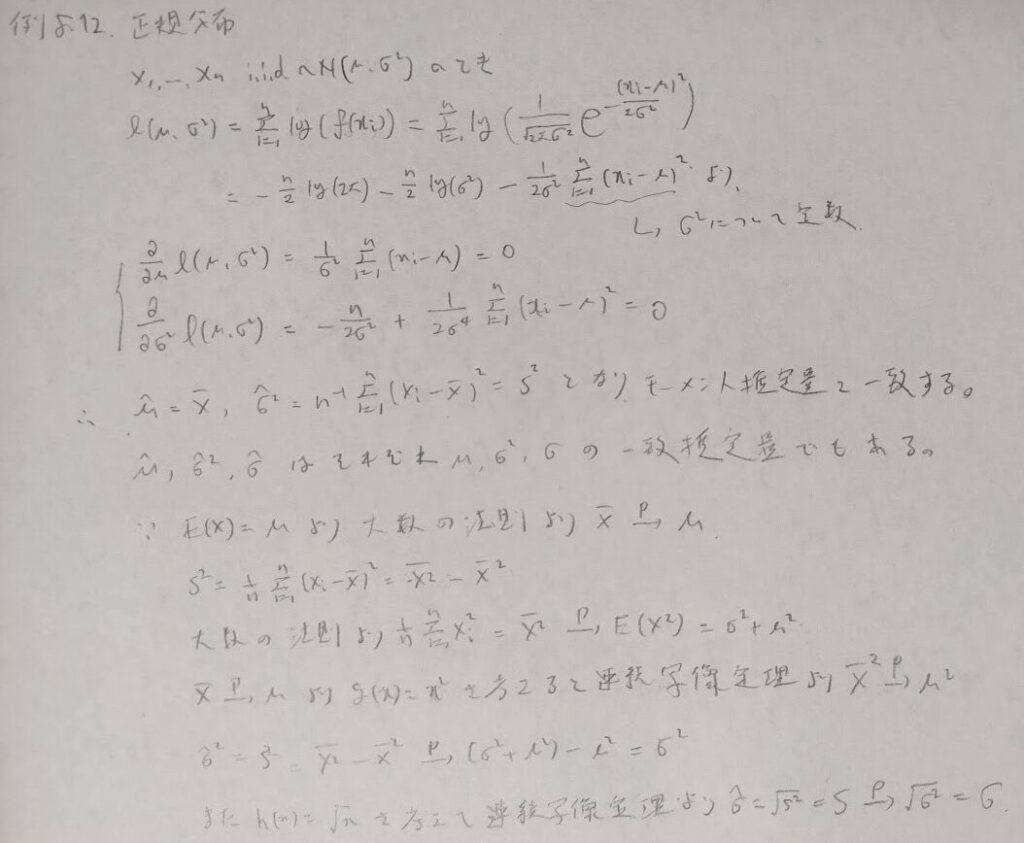
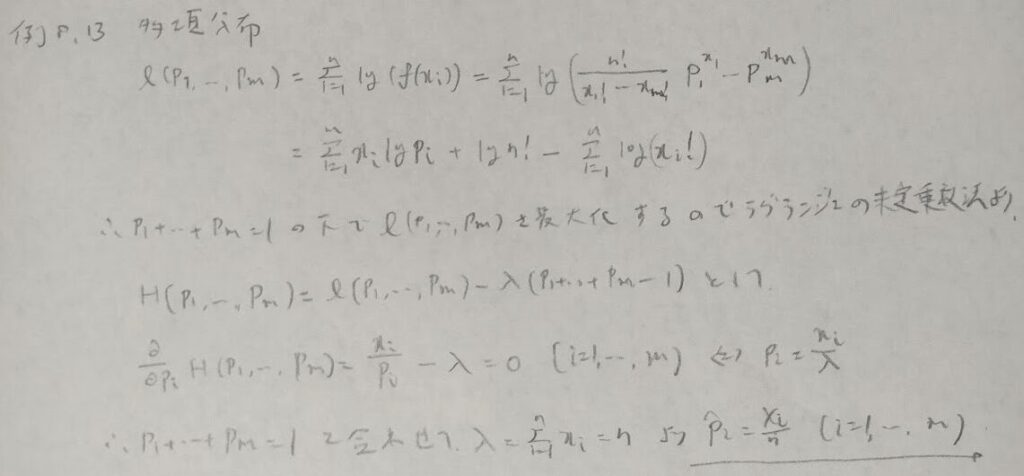
対数尤度から話は広がります。対数尤度の推定量で微分したものをスコア関数といい、その2乗の期待値をフィッシャー情報量といいます。スコア関数の期待値は0であることは重要な定理です。

スコア関数の期待値の内部計算が2階微分で済む(ただしマイナスがつきます)内容は母数が多次元になった時にも拡張されます。
一般に尤度と言われたら同時分布から計算される内容を指します。フィッシャー情報量も何も指定がない場合はnが入った結果になりますが、後の漸近分散ではnを用いないつまり1つの確率変数から導かれたフィッシャー情報量の結果を用います。これは後の母数が多次元の場合も同様です。
またスコア関数とフィッシャー情報量からさらに話は広がります。最尤推定量が持つ漸近正規性は非常に重要な性質です。またこれとデルタ法を合わせることによって更なる定理の拡張が可能になります。また次章のワルド検定の考え方の核となる部分で非常に大切です。
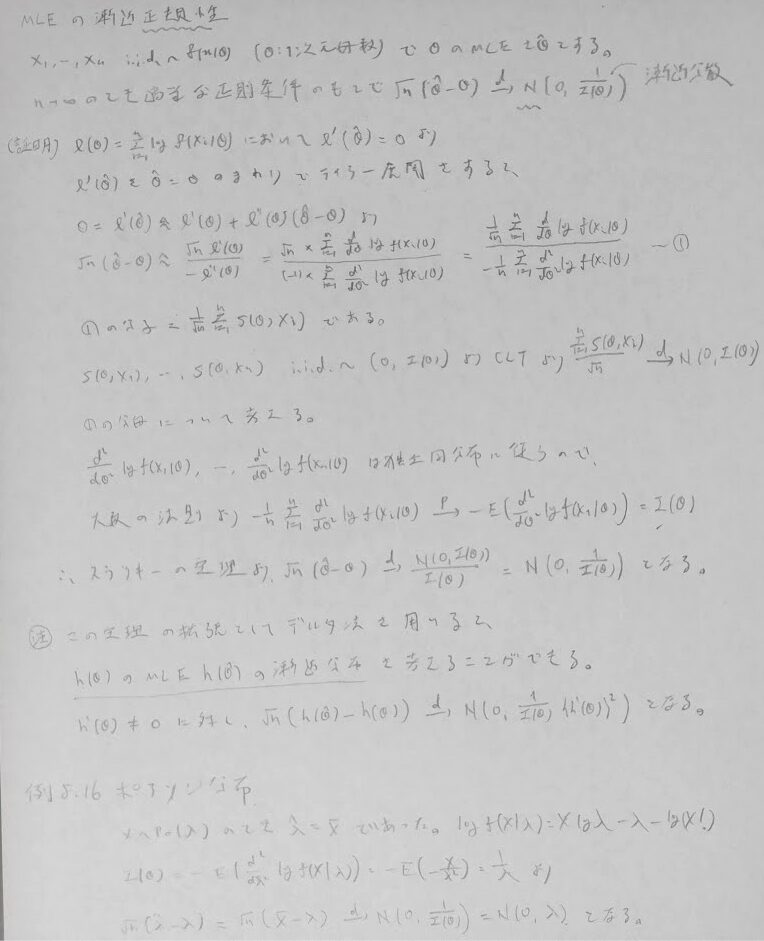
ポアソン分布と二項分布を例にとって考えてみましょう。
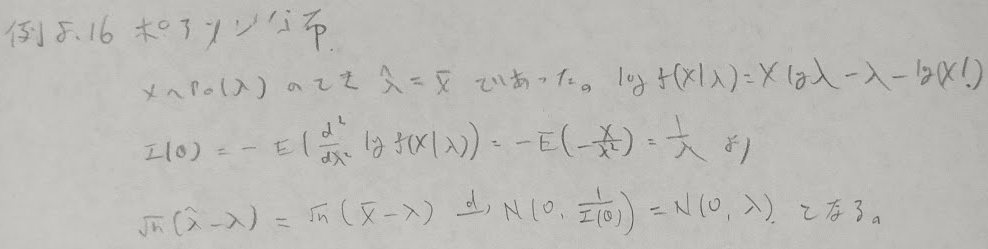

以上の内容を多次元に拡張します。すなわち推定量の次元が多次元の場合を考えます。

具体的に2次元正規分布が漸近分布になる問題を考えます。本問はいくつか注意点があります。
まずフィッシャー情報量行列は対称行列であるので余計な計算を避けましょう。またフィッシャー情報量行列の各成分計算では、2階微分を用いて計算を簡略化します。その代わりマイナス符号がつくことにも注意です。そしてフィッシャー情報量行列はnが入った式ですが、漸近分散の結果ではnは省かれます。
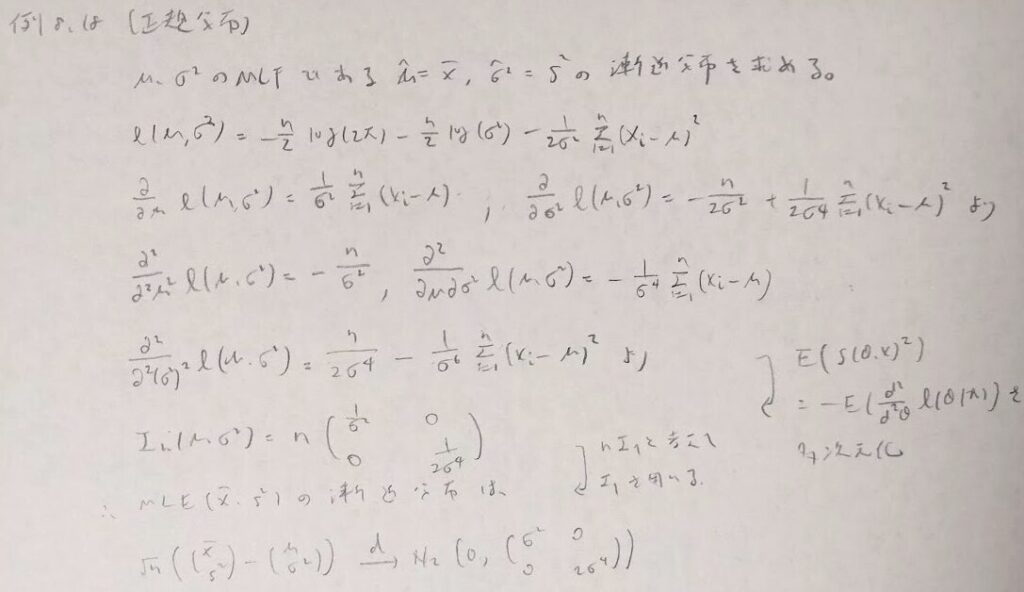
不偏推定量について学習します。バイアス・バリアンス分解まで一気に解説します。
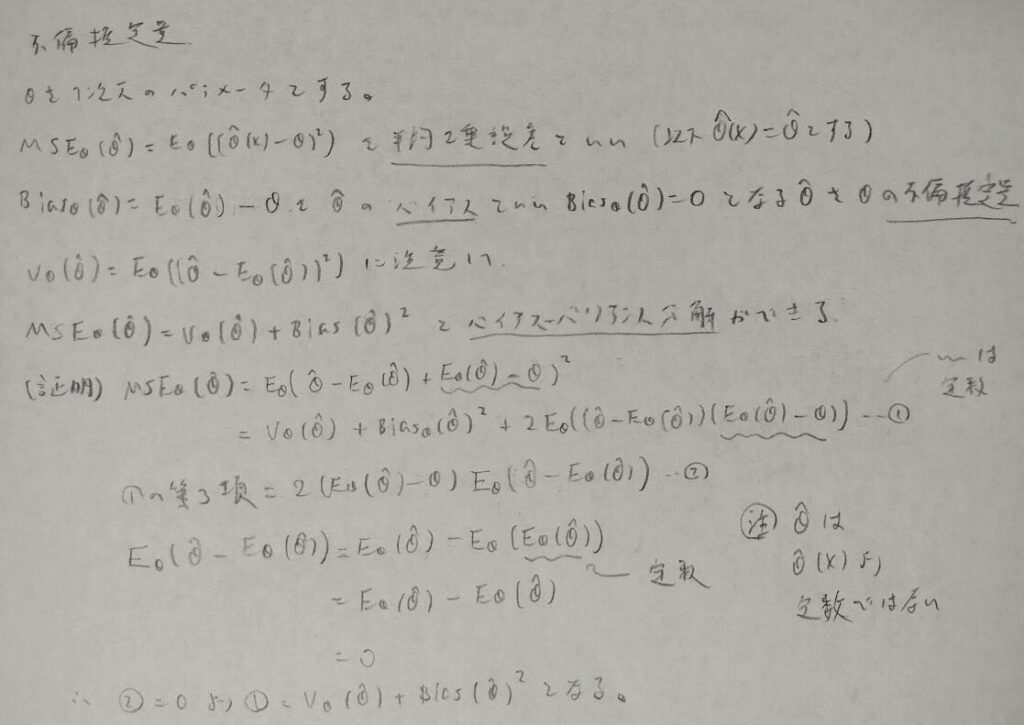
二項分布について例をあげます。
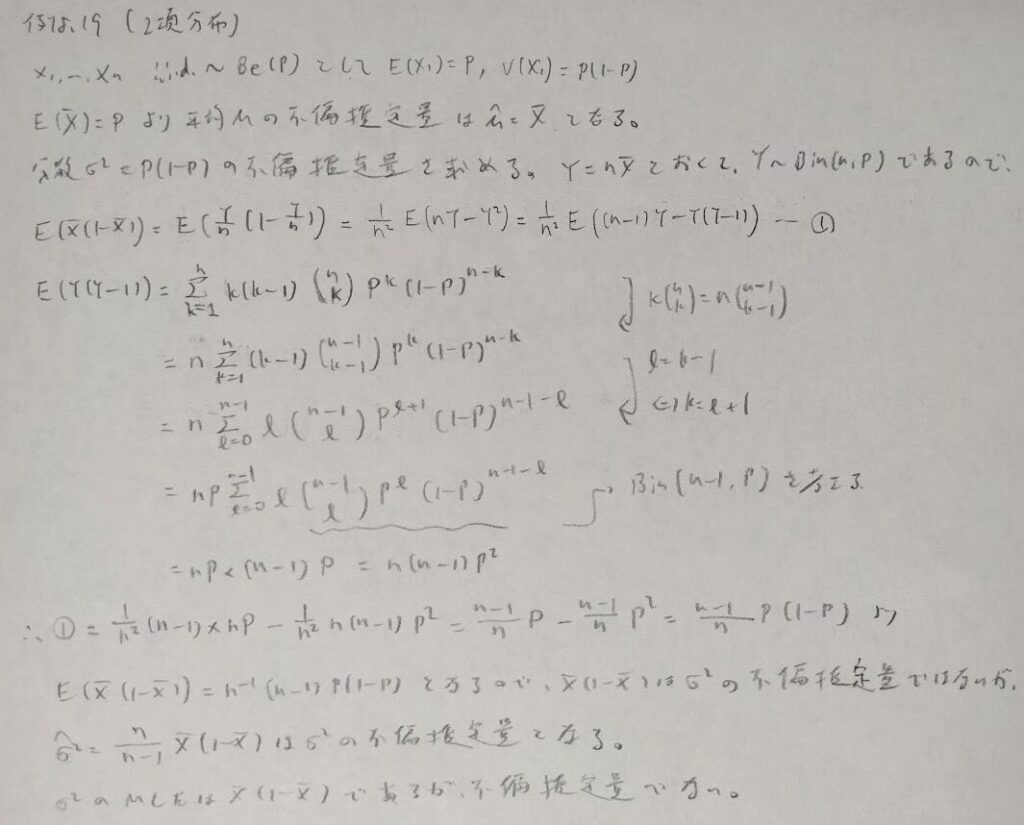
不偏推定量の周辺ではクラメール・ラオの不等式が重要です。ここでは漸近有効性という概念も登場します。
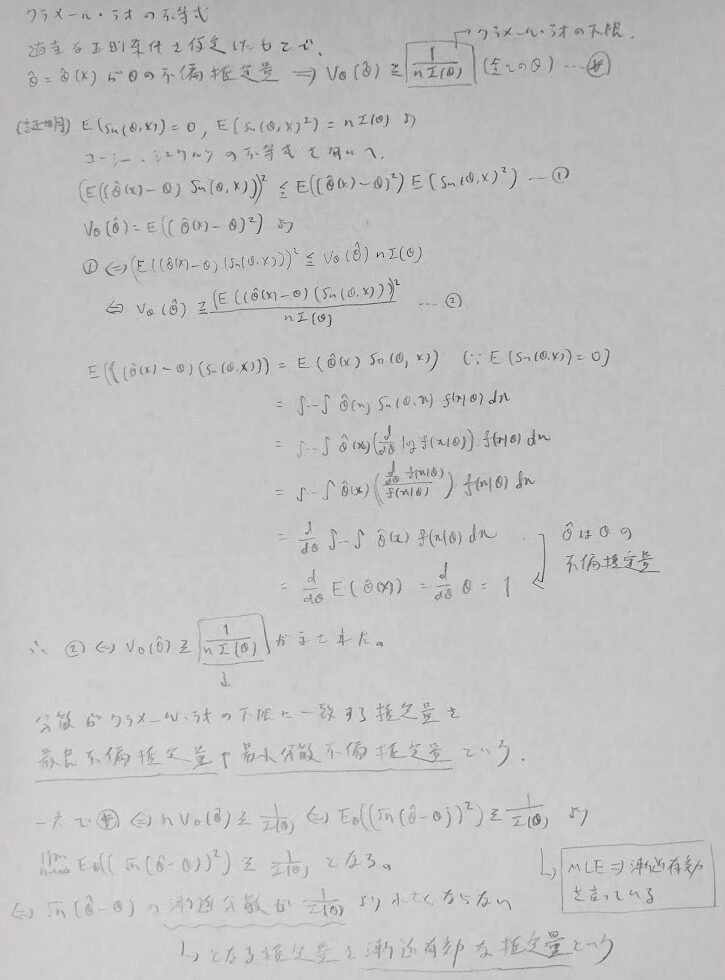
最良不偏推定量の例としてポアソン分布と正規分布をあげます。


最尤推定量→漸近有効という定理を証明します。
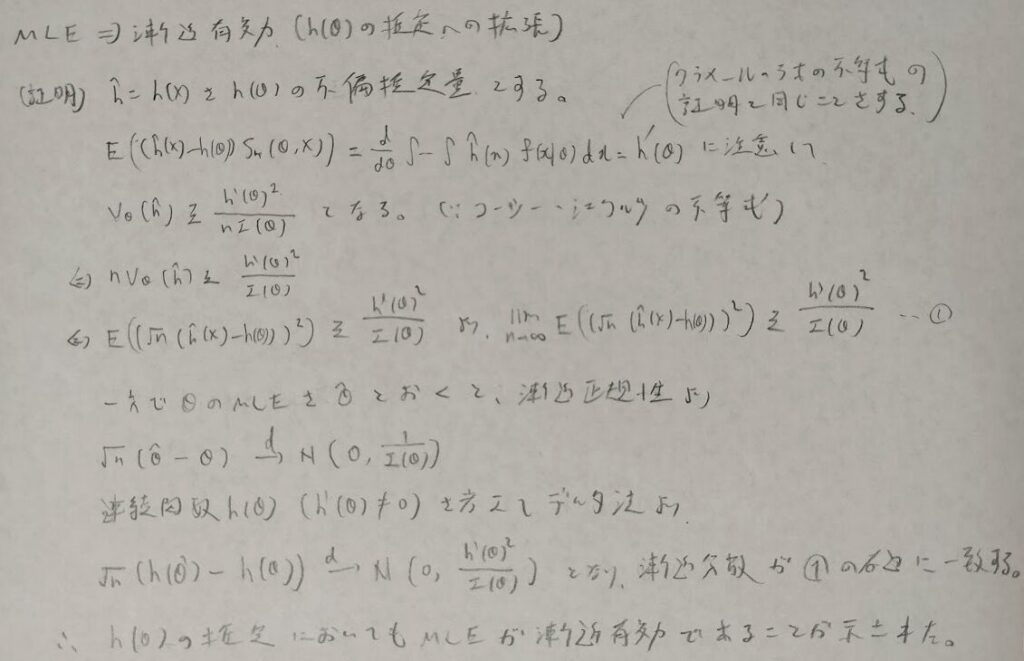
最後に推定量のラスボスであるラオ・ブラックウェルの定理を証明します。

最後に正規分布の例をあげます。当たり前のことをかしこまって証明しています。

統計検定1級青本の第8章の演習問題
問1:指数分布への当てはめ

問2:ポアソン分布への当てはめ
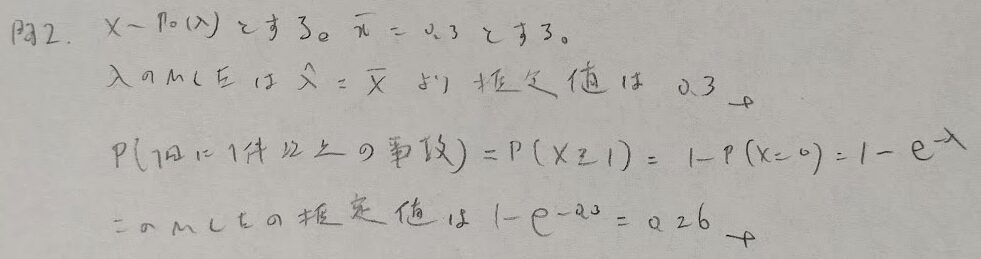
問3:ベルヌーイ分布と推定量
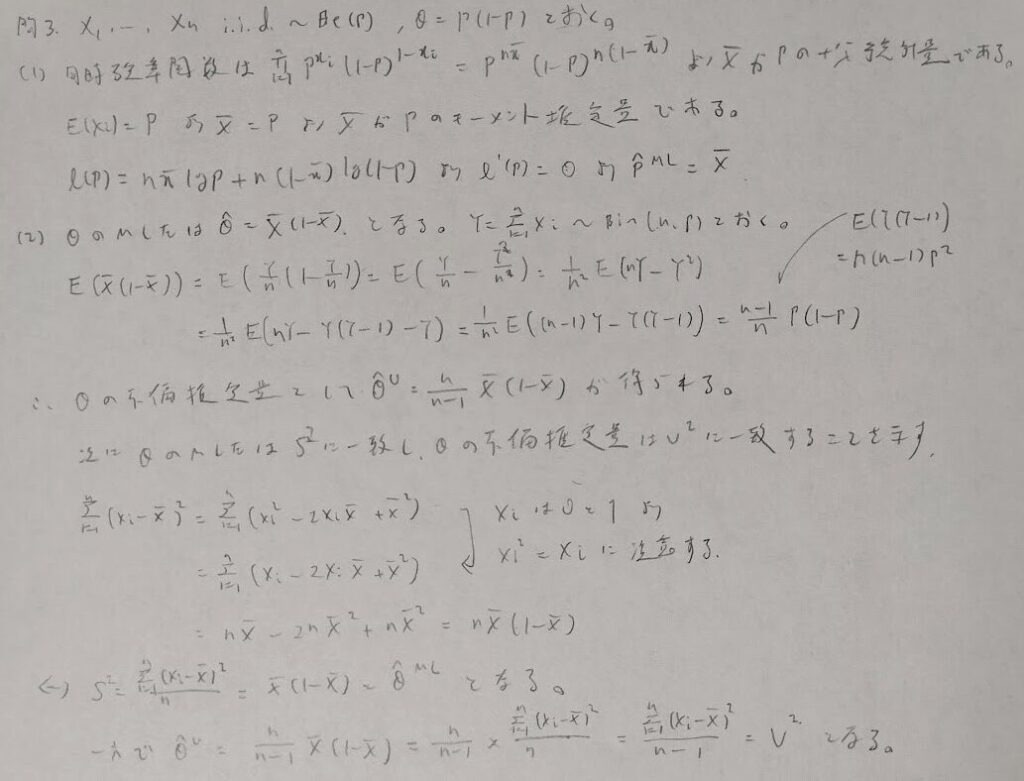
問4:正規分布とクラメール・ラオの不等式
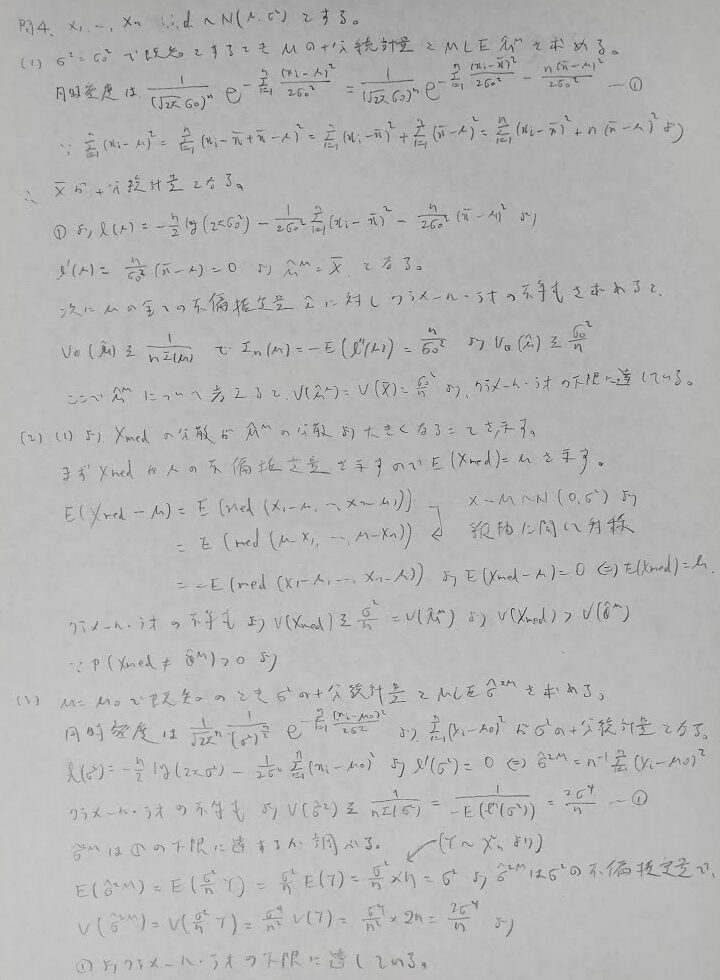
問5:ガンマ分布のパラメータ問題
ボリュームがすごいので小問ごとに分けます。
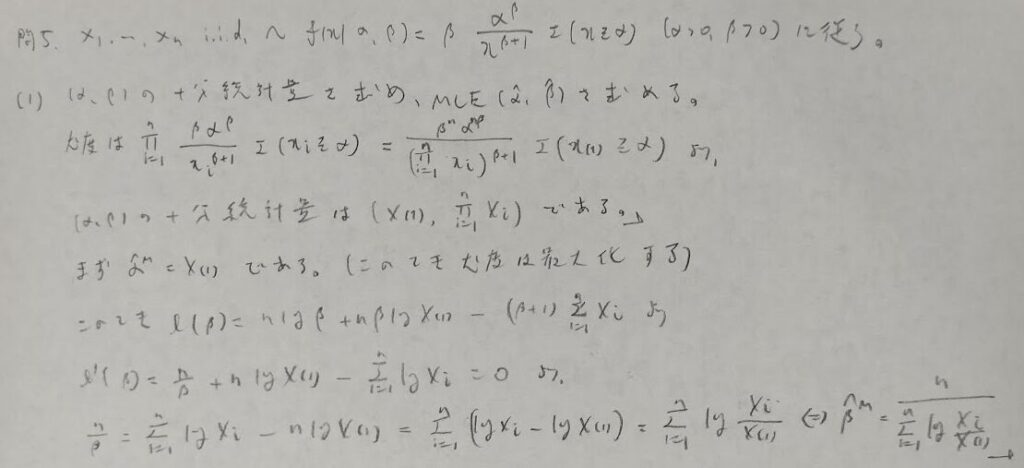
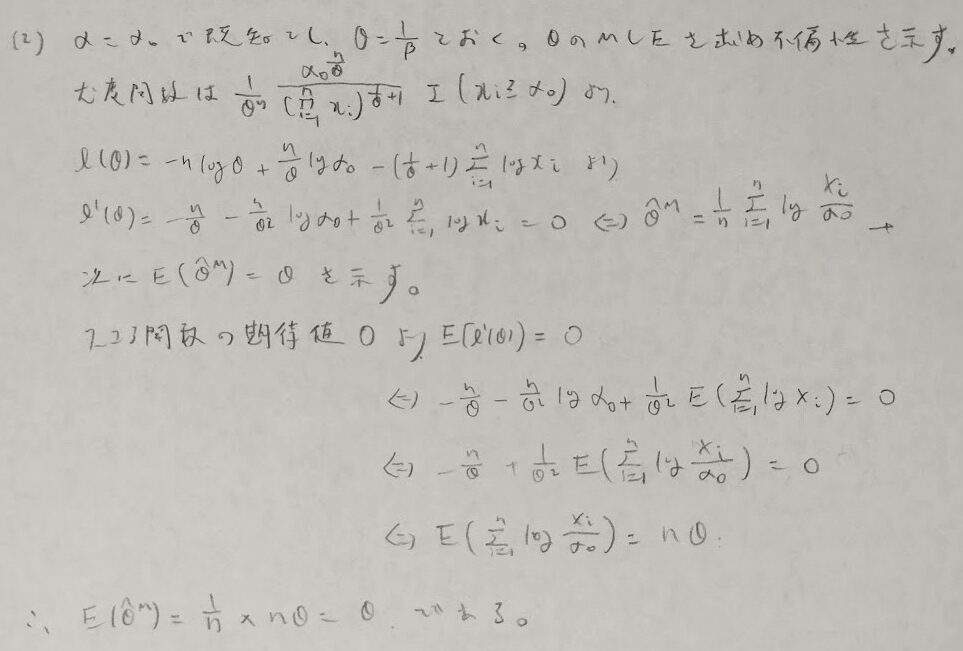
スコア関数が本格的に登場しました。
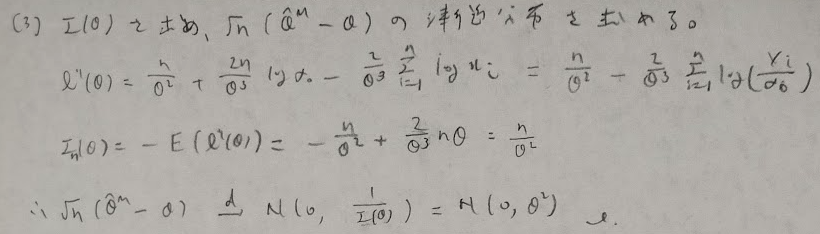
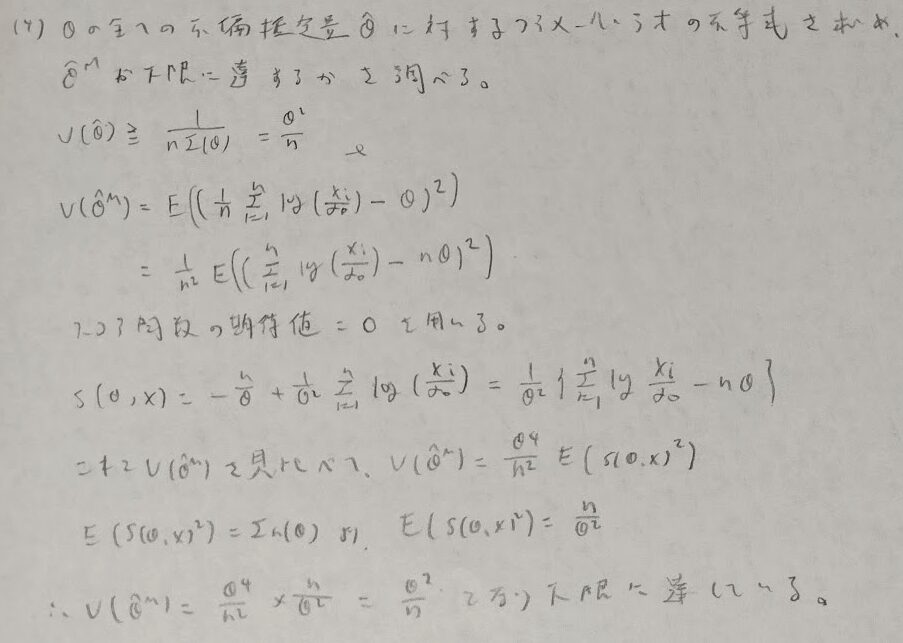
問6:十分統計量
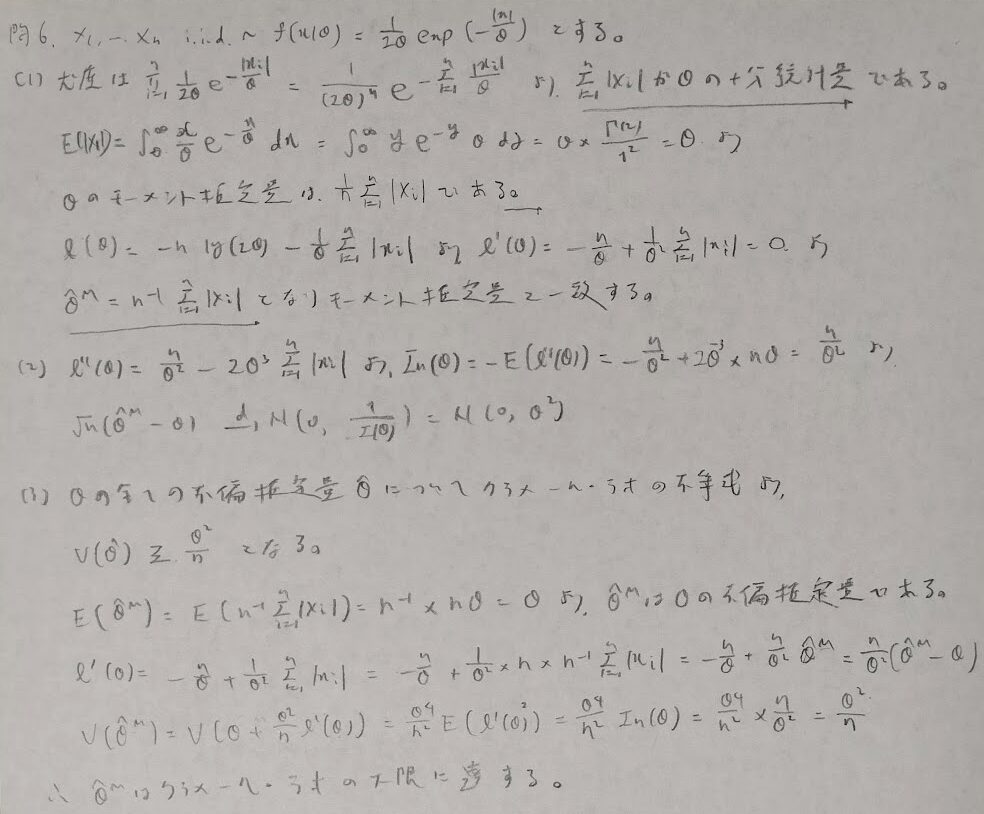
問7:多項分布と不偏推定量

問8:十分統計量が最小統計量
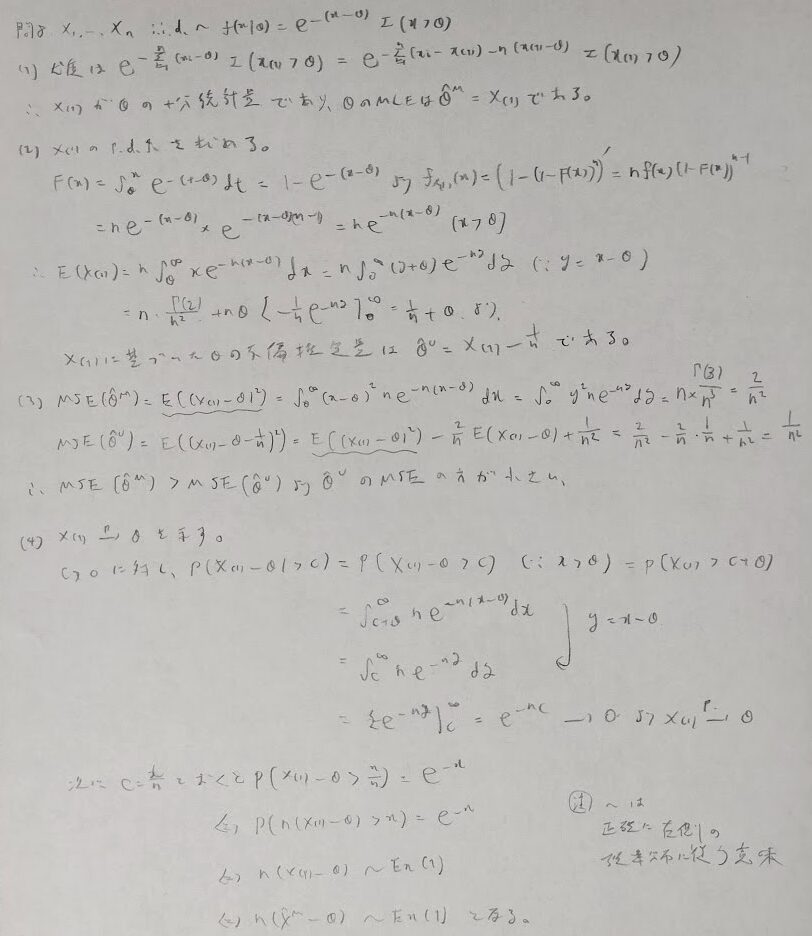
問9:指数分布の総合問題
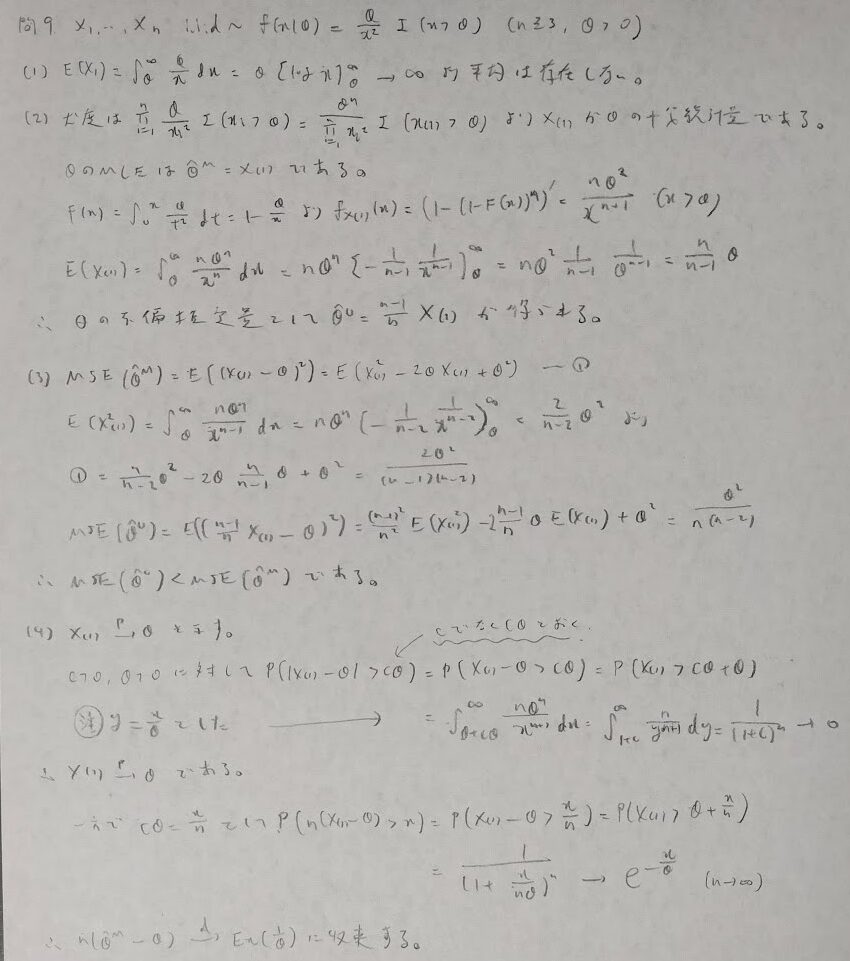
問10:行列利用

問11:スコア関数とディガンマ関数
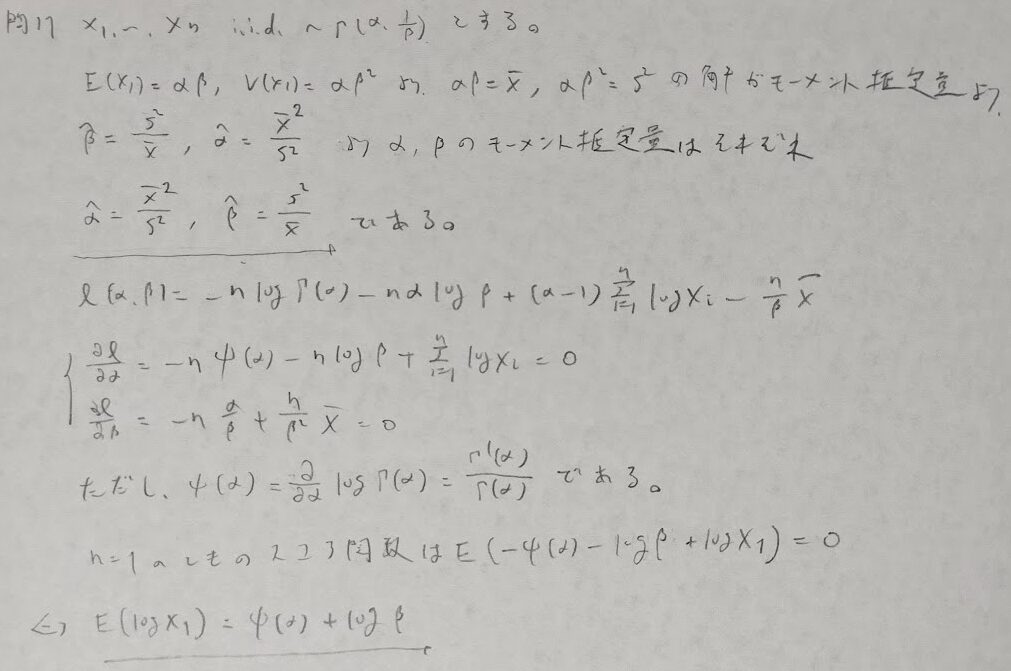
以上で推定(点推定)の内容は終了です。本章は統計検定1級でも頻出の箇所ですので、その分ボリュームも増えました。しかし『データ解析のための数理統計入門』の問題は良問が多いことには変わりありません。何度も繰り返して学習し、統計検定1級の合格を目指しましょう!







