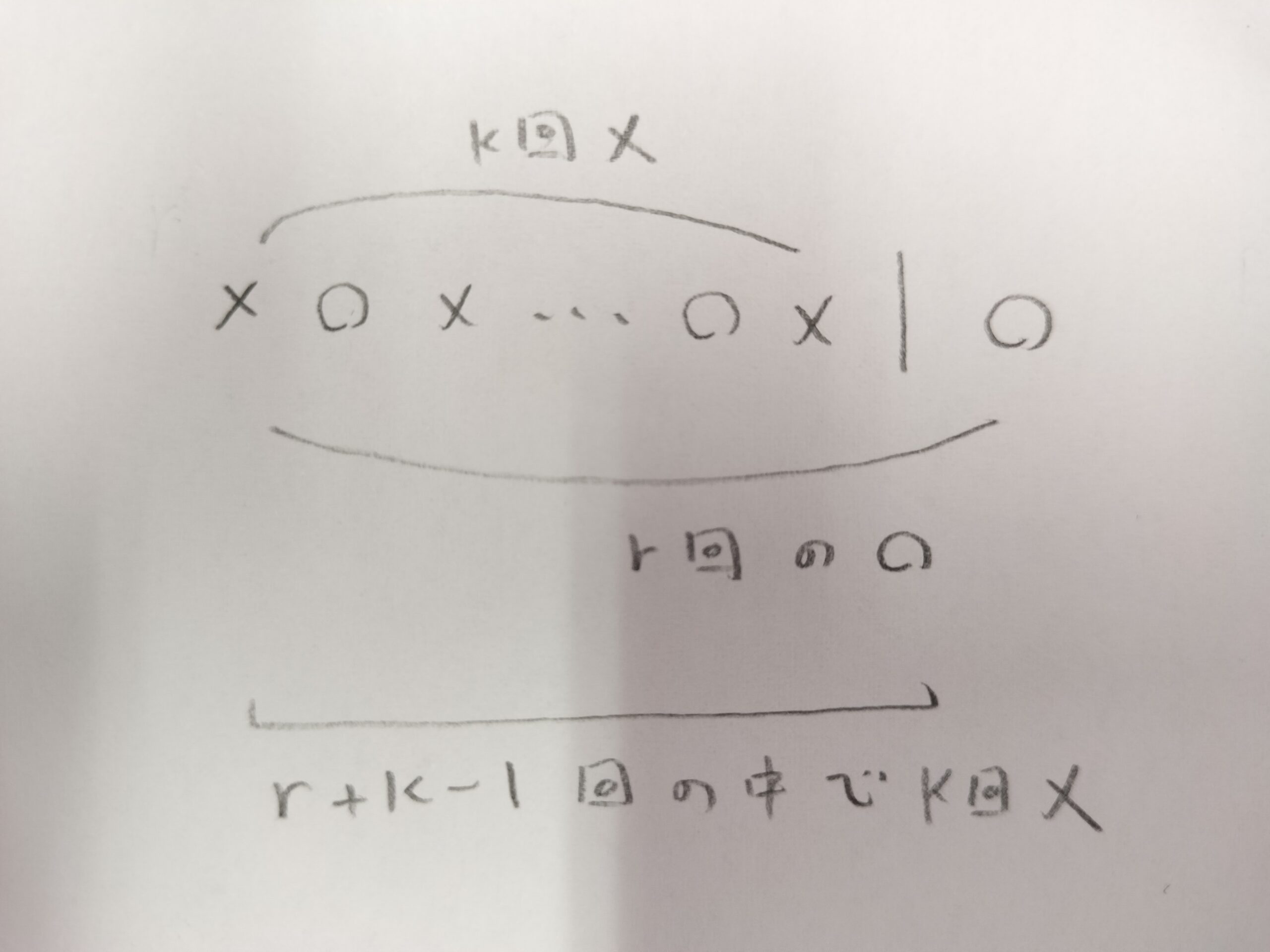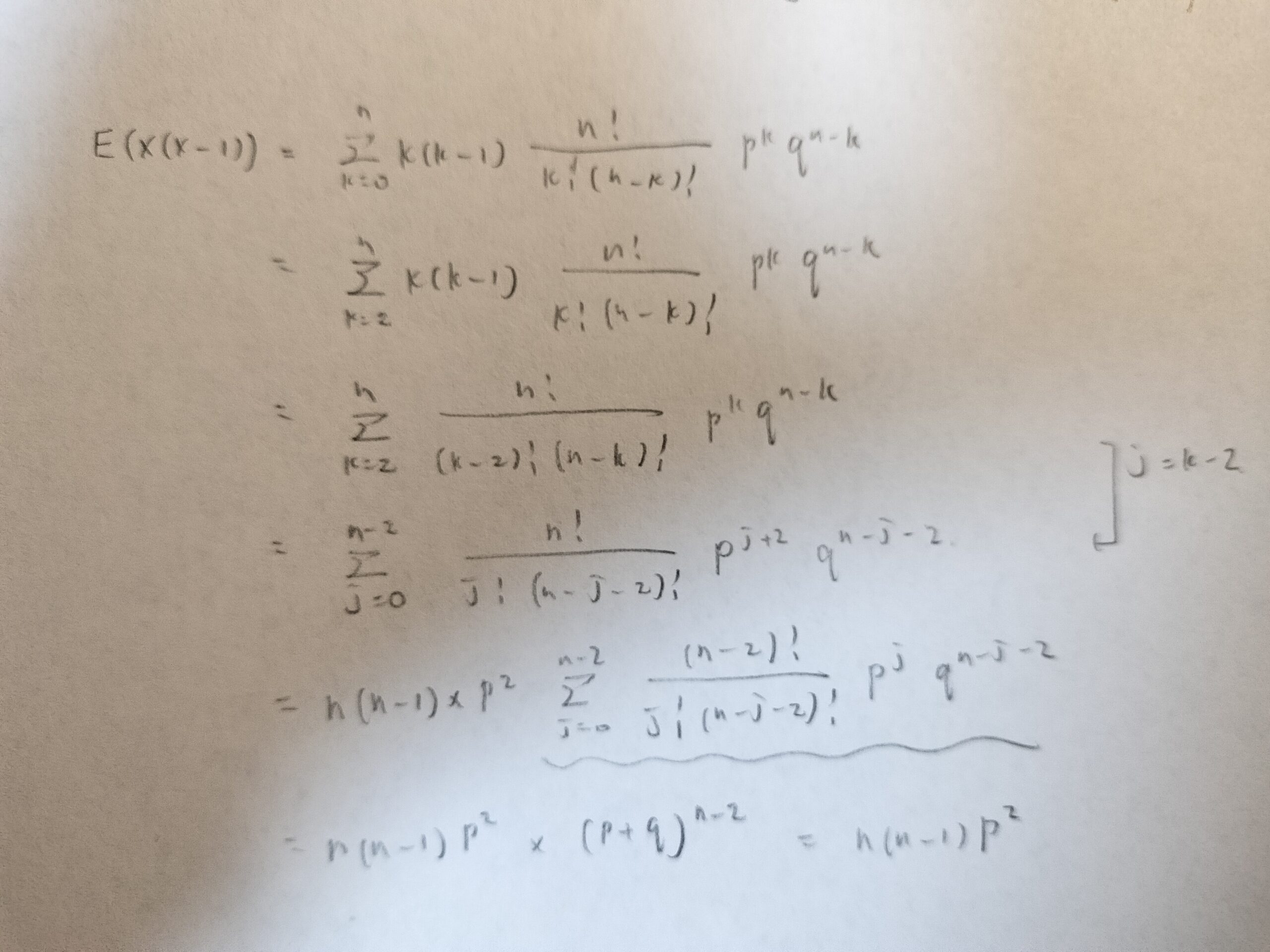二項分布の次は負の二項分布が登場します。
数理統計の参考書によって登場する確率分布の順は様々ですが、流れ的には負の二項分布を扱った方が自然かなと思います。
なぜ負の二項分布というのかあれこれ考えてましたよね?笑
このように二項分布と負の二項分布は何らかの試行についての回数の分布であることは共通事項です。
成功回数を主役にする場合と、失敗回数を主役にする場合とで確率関数が異なります。
突然に負の二項分布からスタートすると頭が混乱すると思いますので、幾何分布から説明していきたいと思います。
幾何分布はなぜ幾何というのかの考察
幾何分布とはいったいどのような分布で、どのような確率関数を持っていますか?幾何と呼ばれるから図形が関係していますか?
順に説明していきます。
次のような無限級数を考えます。無限級数といっても単純な無限等比級数を扱います。計算結果が1になることから、確率和が1という事実と対応させて考えています。
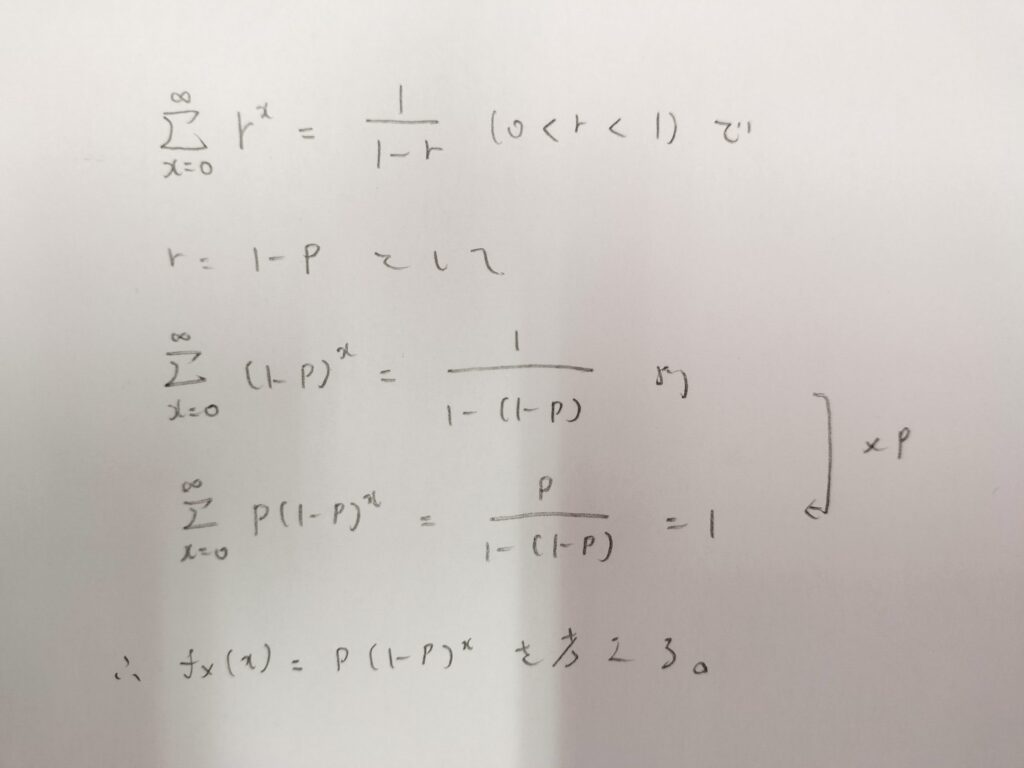
途中式でのp倍なども後半で登場する負の二項分布の式変形の際にも使いますので意識しておいてくださいね。
最後に登場した式が確率関数ですね!
では次にこの数式が持つ意味を考えたいと思います。
幾何分布の意味とは、試行を繰り返し行ったときに、初めて成功するまでの失敗回数を考えていきます。
失敗回数をXとしたときに、確率変数Xが従う分布を幾何分布といい、Xは上式最後の式を確率関数に持ちます。
なぜ幾何分布は幾何という名前がつけられているのでしょうか?
等比数列のことを幾何数列ともいうことが理由です。等比数列は相似の意味をもつため、図形的には繰り返し図形が登場することになり、図形色が強い数列です。図形は幾何学で扱うので幾何分布という名前が付けられているのだと考えています。
幾何分布の考えをマーケティングで活躍する負の二項分布に拡張します
二項分布が成功回数を主役としたので、負の二項分布は失敗回数を主役とします。
幾何分布は初めて成功するまでに失敗した回数を考えたので、今度は初めて成功するの「初回という意味での初めて」という制限をつけずに考えたいです。
このような自然な考えから幾何分布は負の二項分布へと発展していきます。
(初めて)r回成功するまでに失敗した回数を考えます。この失敗回数をXと置いたときにXは負の二項分布に従います。
下の図ではX=kのときを考えて確率関数を導出するためのイメージ図となっています。
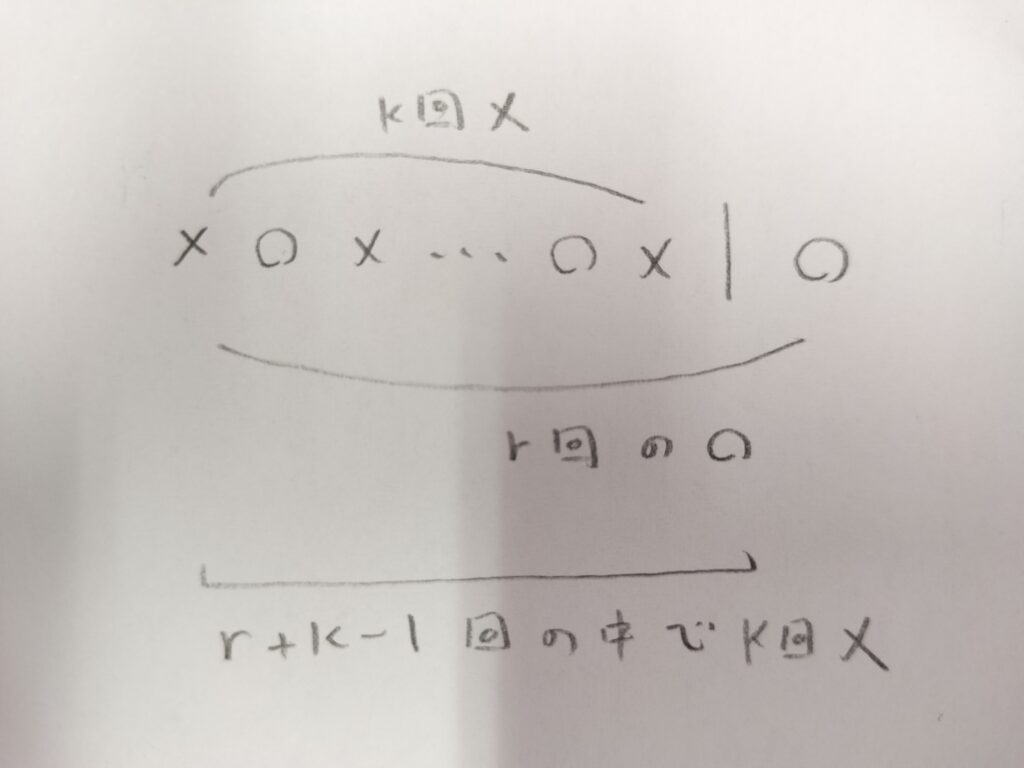
次に負の二項分布の確率関数を算出していきます。
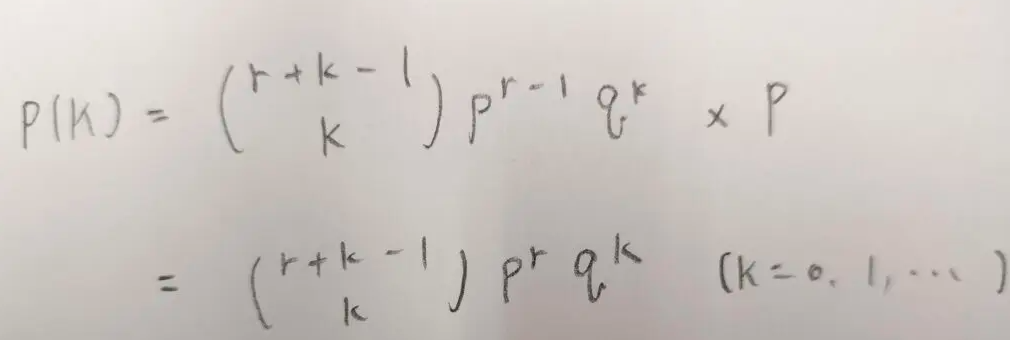
この最後の式が負の二項分布の確率関数となります。
pを掛けている理由は、最後に成功して終わるからですね!
統計検定1級やアクチュアリー数学の試験では負の二項分布はさまざまな文字を用いて定義されます。この記事でも慣れるため、いろんな文字を使っていきます。混乱を避けるためにも、上のようなイメージ図を書けるようにしておくとミスが起こらずに便利です。
この確率関数は本当に確率和が1になるのか不安です。証明はどうやってやるのですか?
そのように思いおますよね。僕もそう思っていたので気持ちはわかります。実は確率和1の式から期待値や分散が導けると紹介する参考書『現代数理統計学の基礎』もありますので、確率和1を証明しておきましょう。
負の二項定理を知っていないと証明が大変困難です。まずは負の二項定理を導いたときの副産物として確率和が1(全確率1)となることを導いてみます。
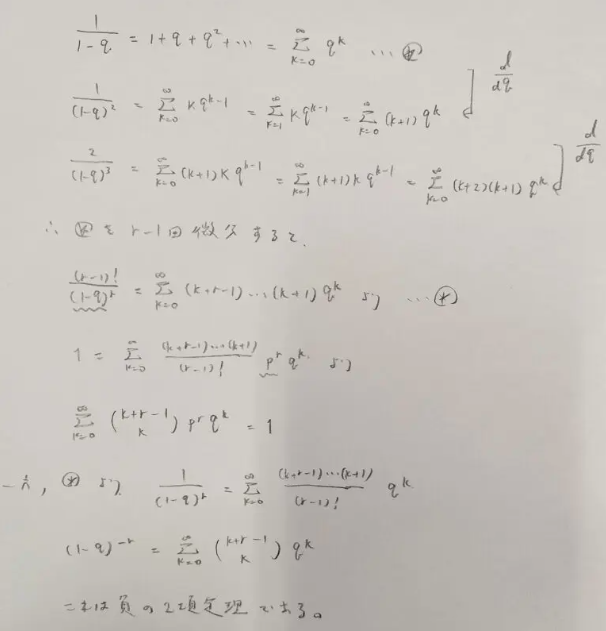
途中で微分したり両辺に何か数をかけたり技巧的な感じがしますが、ポイントはありますか?
まずはシグマの表示では意味のない箇所は省くことが大事です。その上でなるべく0スタートにすることがポイントです。
実は上の式変形の中盤で確率和が1が証明されていますが、なんか長いですよね笑
ということで、次は負の二項定理を知っていることを前提とした証明を紹介します。
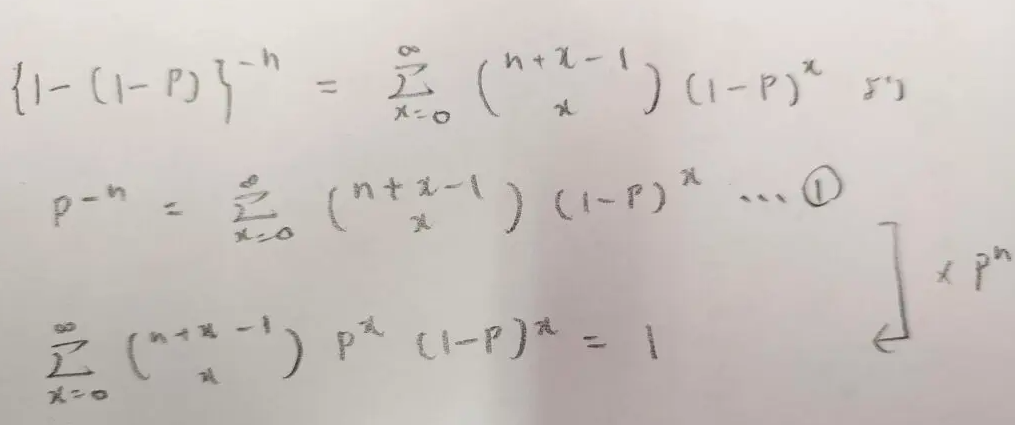
とてもシンプルな証明ですね!
それも当然で、負の二項定理そのものが示すべき式とほぼ同値なことだからです。
下記の本が統計学を用いたマーケティングの本として有名みたいですね。
負の二項分布の期待値と分散を計算します
いよいよ統計検定1級などで問われる負の二項分布の期待値と分散の証明部分です。
①確率母関数を求めてから微分をすることによって期待値と分散を導く方法
②確率和1の式からうまく期待値と分散を導く方法
③期待値と分散を直接導く方法
この3つがありますが、この記事の流れから②の方法がわかりやすく覚えやすいと思いますので、②のパターンを紹介します。
『データ解析のための数理統計入門』に掲載されているアイディアとなります。
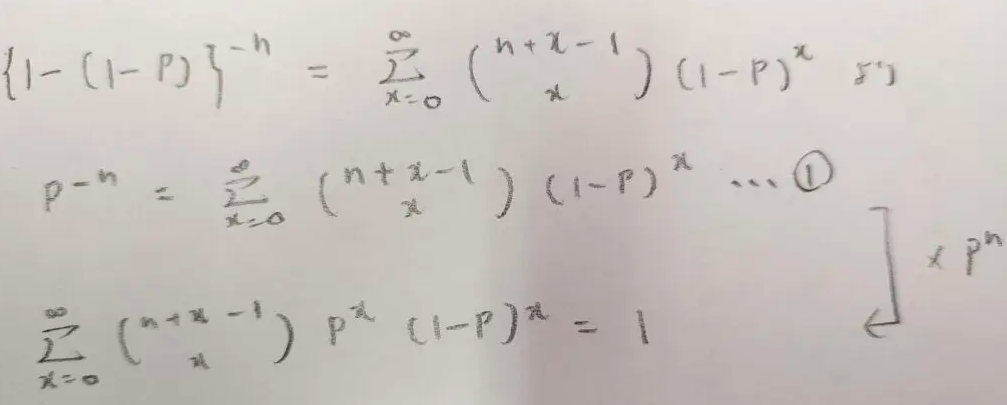
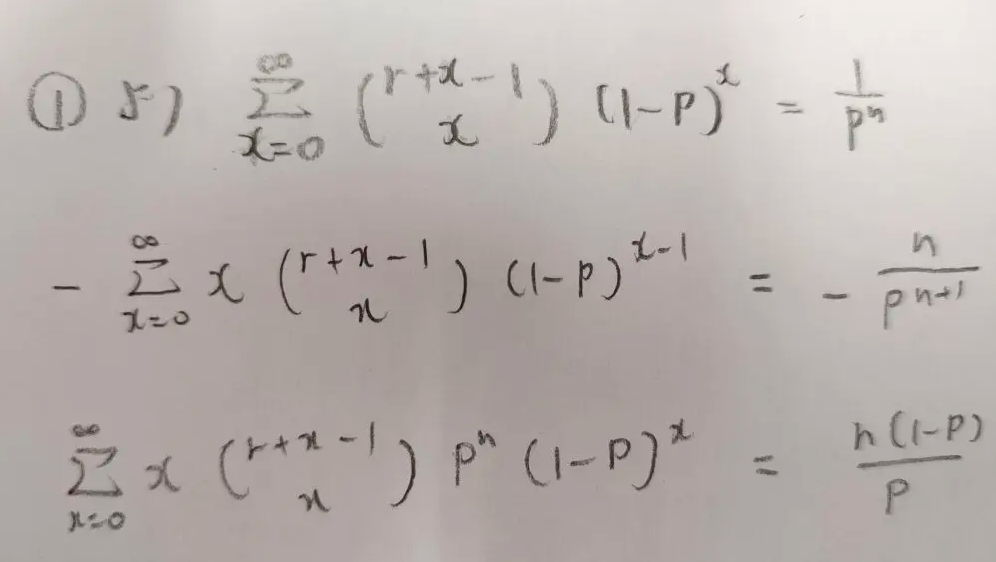
1枚目は確率和1の証明に用いた図です。
2枚目の2行目は1行目の式をpで微分しています。3行目で期待値の定義と合致するように2行目から3行目にかけて両辺にpの式を掛けています。
なるほど!期待値の定義式と合致するように式を微調整していくのですね!
次に分散の式を導きます。そのためにまずはX(X-1)の期待値を求めます。
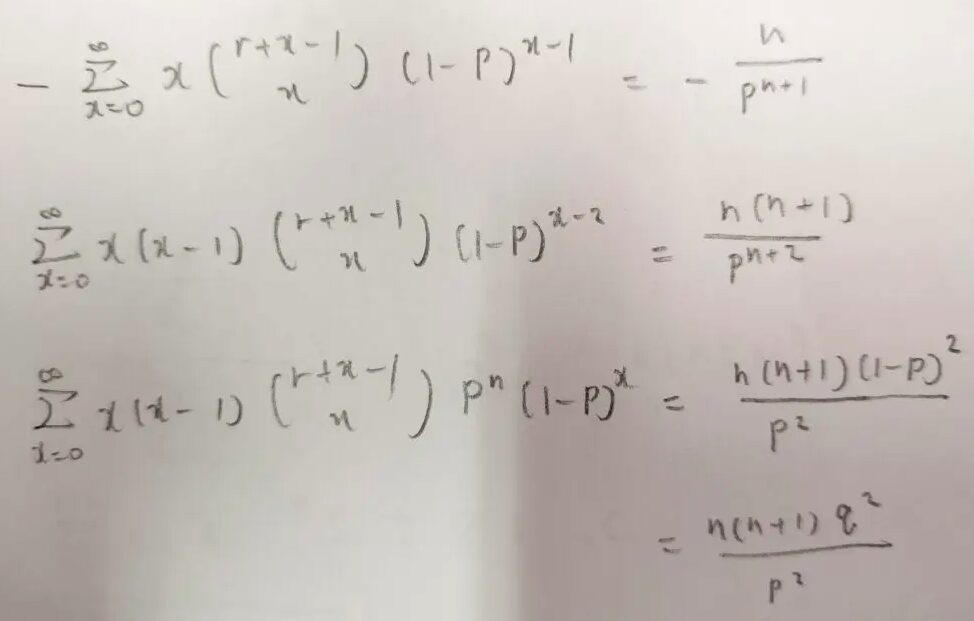
上の式はさきほどの期待値を導いた図の2行目の式と同じ式です。この式から始めます。
また微分してますね!笑
その通り。微分したあとにX(X-1)の形の期待値と合致するように数式を整えます。
二項定理も負の二項定理もXやX(X-1)の形の期待値と相性が良いです。これは確率関数にC(組み合わせで用いるコンビネーション)が含まれているためだと考えています。X(X-1)(X-2)の期待値も類推できますね。
最後に分散を出して、期待値との結果をあわせてまとめておきます。
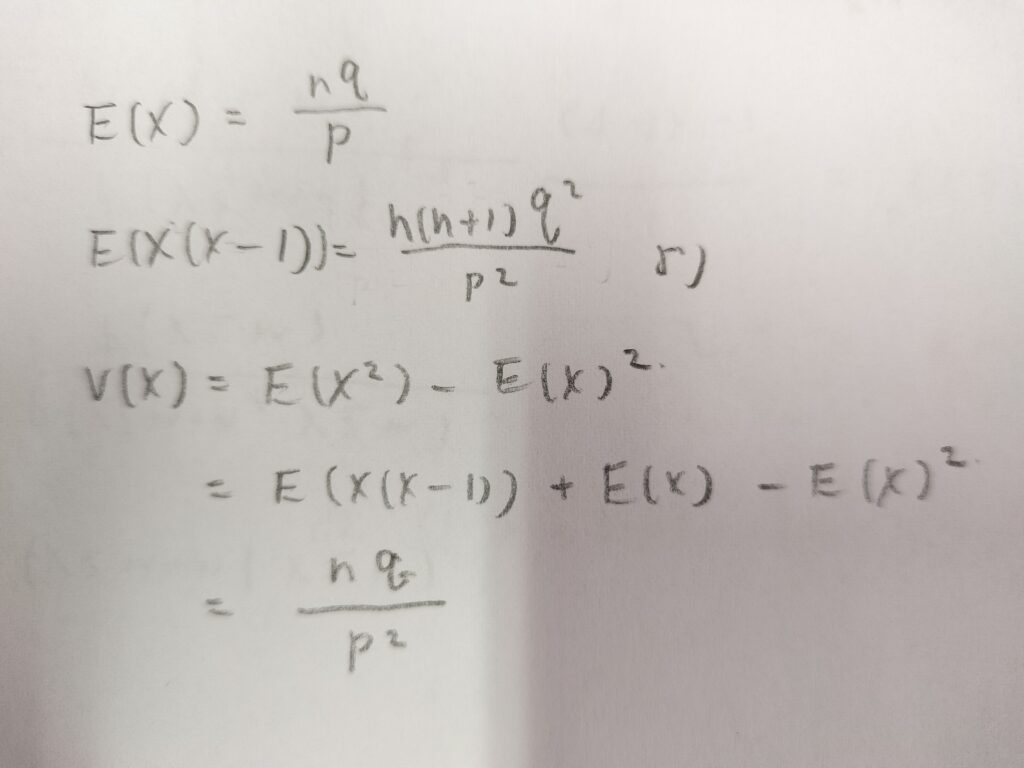
nって整数ですか?
いいえ正の実数です。このような誤解が生じてしまうため、一般には次のようにαなどの記号を用いてnを表現します。たとえば『アクチュアリー試験 合格へのストラテジー 数学 第2版』などで採用されています。
負の二項分布の英語名は、negative binomial distributionです。その頭文字を用いてNB(α,p)と表記します。
幾何分布は負の二項分布の特殊な例で英語名はgeometric distributionです。そのためGeo(p)やGe(p)などで表されます。
負の二項分布においてαを1とすると幾何分布になります。
以上を踏まえて、負の二項分布と幾何分布の期待値と分散をまとめておきます。
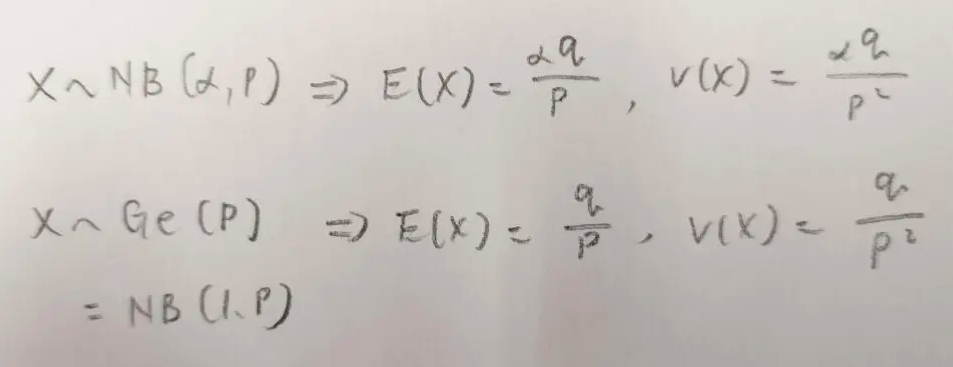
最後にこの記事で主に参照した書籍を紹介します。
2023年の統計検定1級において、本書の第2章~第7章までを演習問題を含めて完璧にした方が合格されたようです。過去問よりも上か、それと同じくらい大切な本なのだと実感しました。
本書の練習問題では、負の二項分布の期待値と分散を微分方程式を立てることによって導いてます。本書は前著と比べて証明が洗練されている印象です。定理によってはこちらの方が読みやすい証明もあります。
どちらの参考書も素晴らしいです。僕もこれらを読み込んで理解を深めていきたいと思います。