統計検定準1級のワークブック『日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック』を用いた学習の第4部として「種々の応用」を扱います。
種々の応用とは「確率と確率分布」「統計的推測」「多変量解析法」以外の分野になります。
種々の応用はこれまでに学習してきた3つの部の内容が元になりますので、まずはこちらの内容を理解してから進みましょう!
統計検定準1級ワークブック第1部→確率と確率分布
統計検定準1級ワークブック第2部→統計的推測
統計検定準1級ワークブック第3部→多変量解析法
統計検定準1級ワークブック解説:第14章『マルコフ連鎖』
例14−1
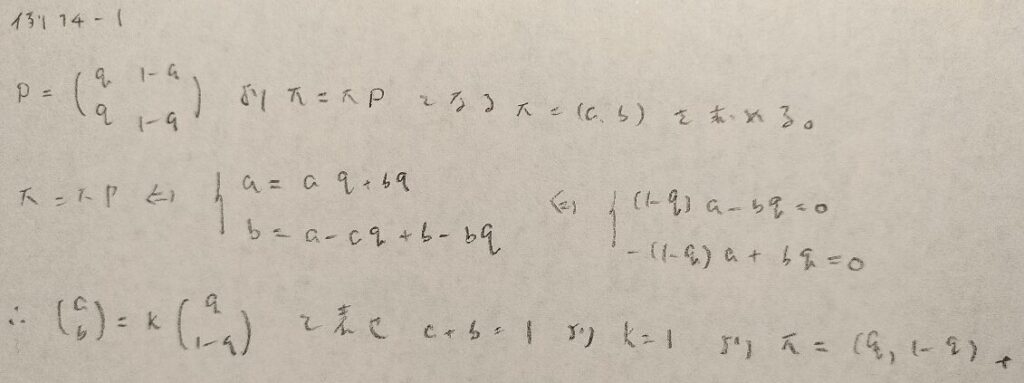
例14−2
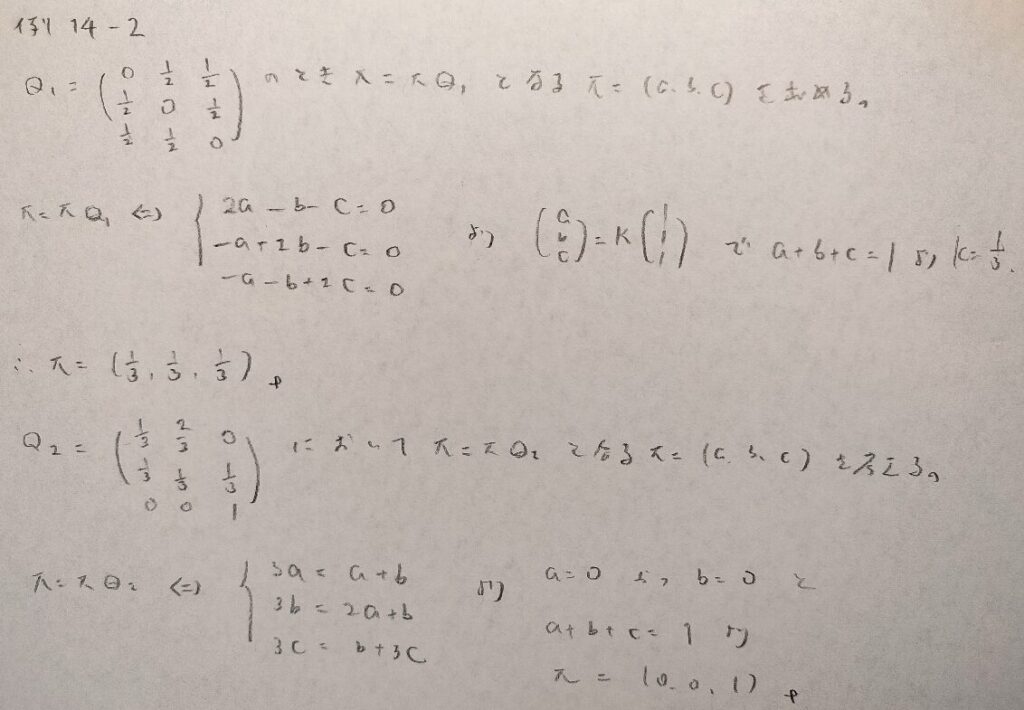
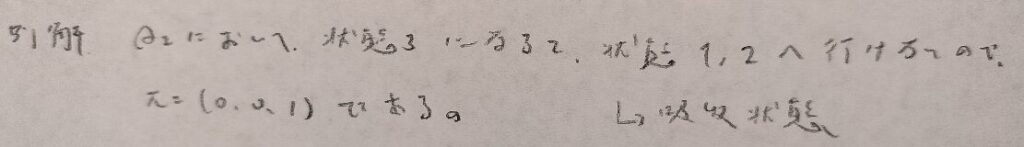
例14−3
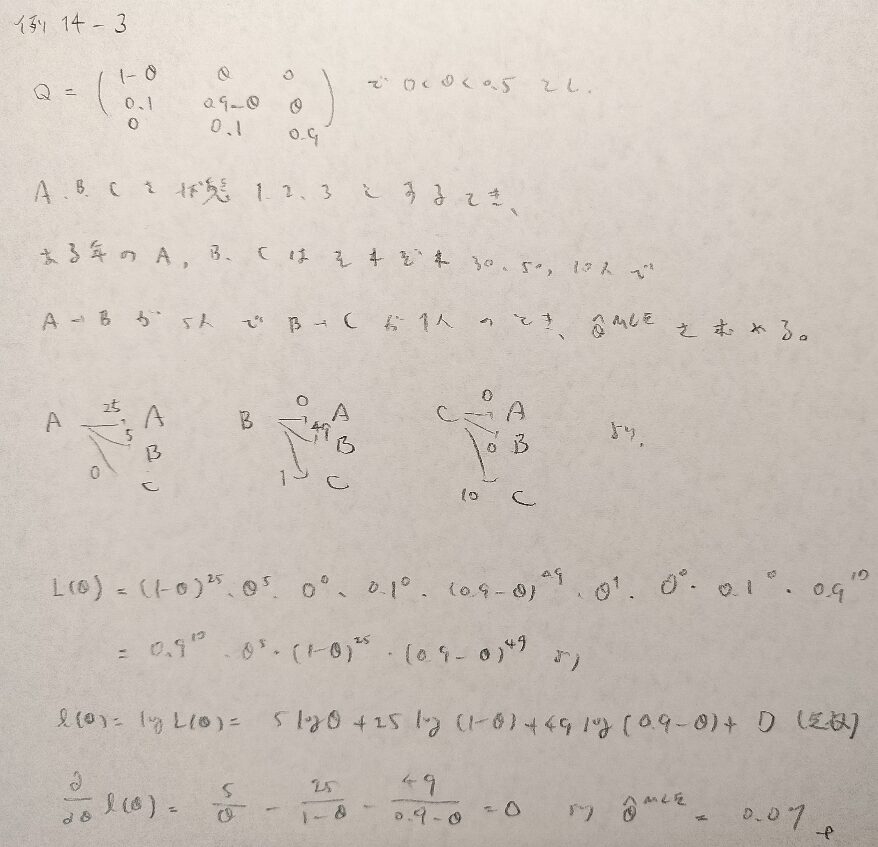
問14.1
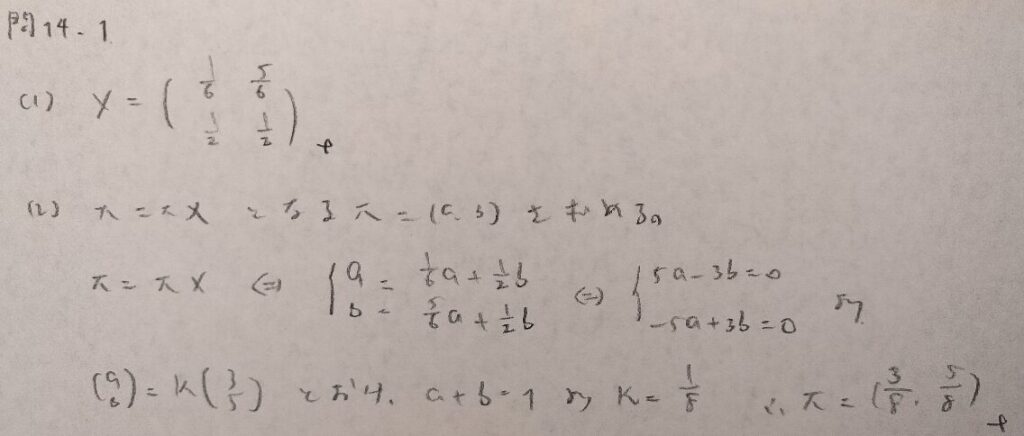
問14.2
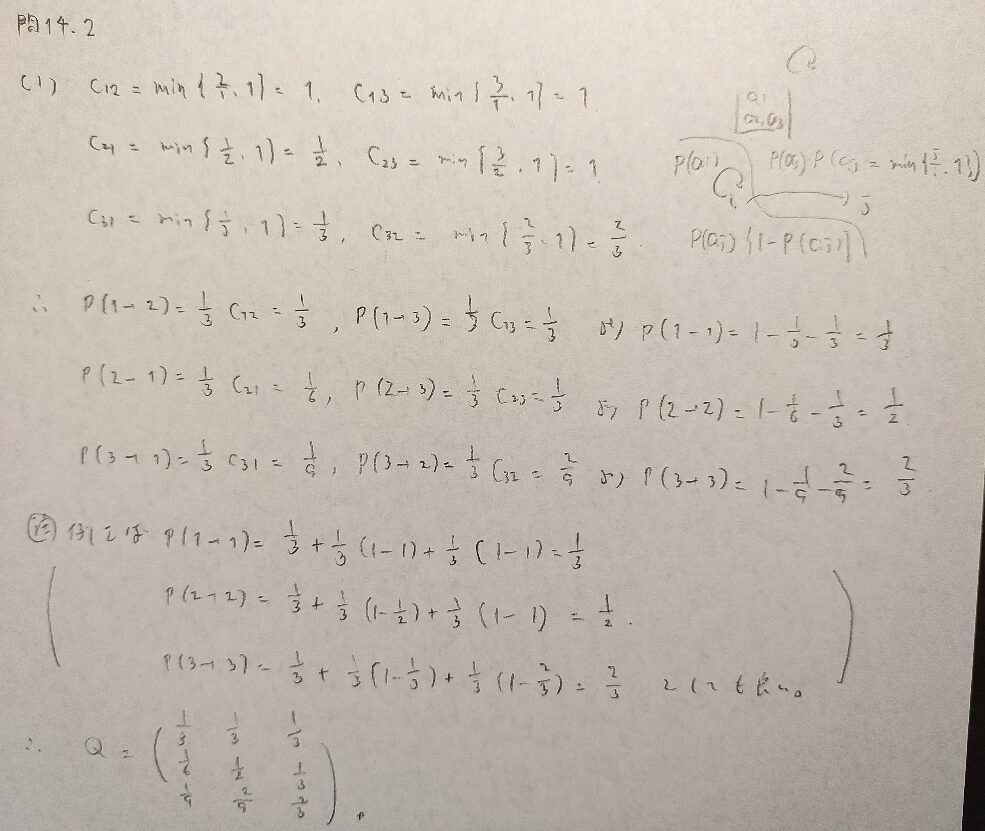
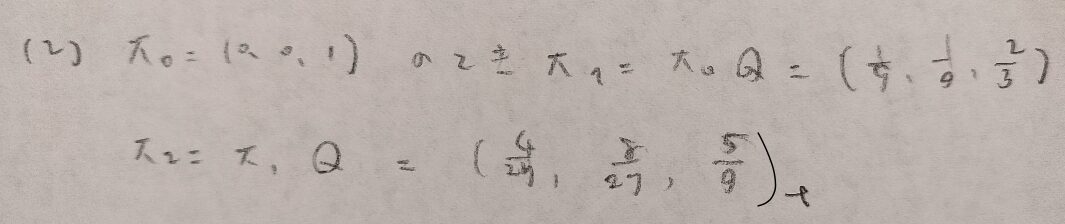
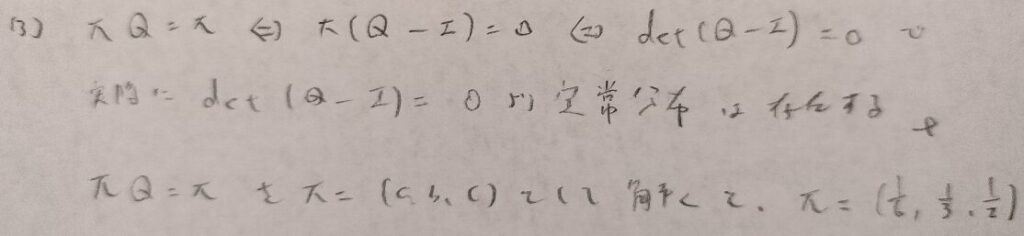
問14.3

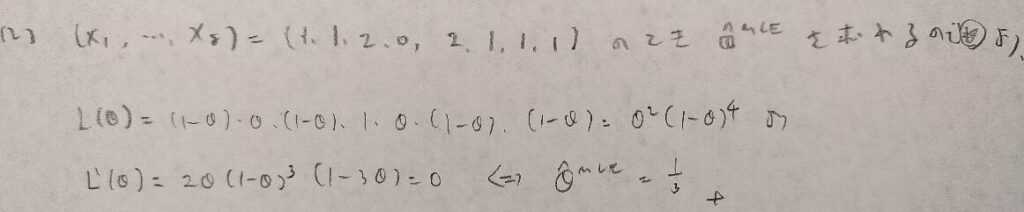
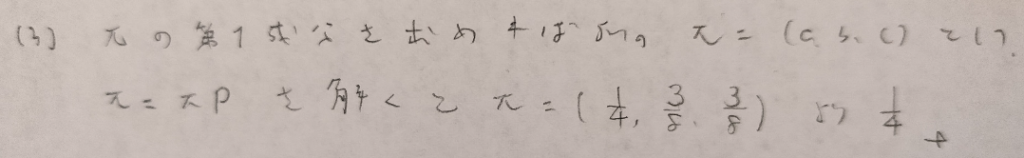
第14章メモ
推移確率行列を求めて定常分布を出す流れが頻出です!
定常分布という名前の意味は、πの各成分の和が1であるので確率分布の性質を満たし、定常性(以後ずっと変わらない)を満たしているということに由来しています。
統計検定準1級ワークブック解説:第15章『確率過程の基礎』
例15−1
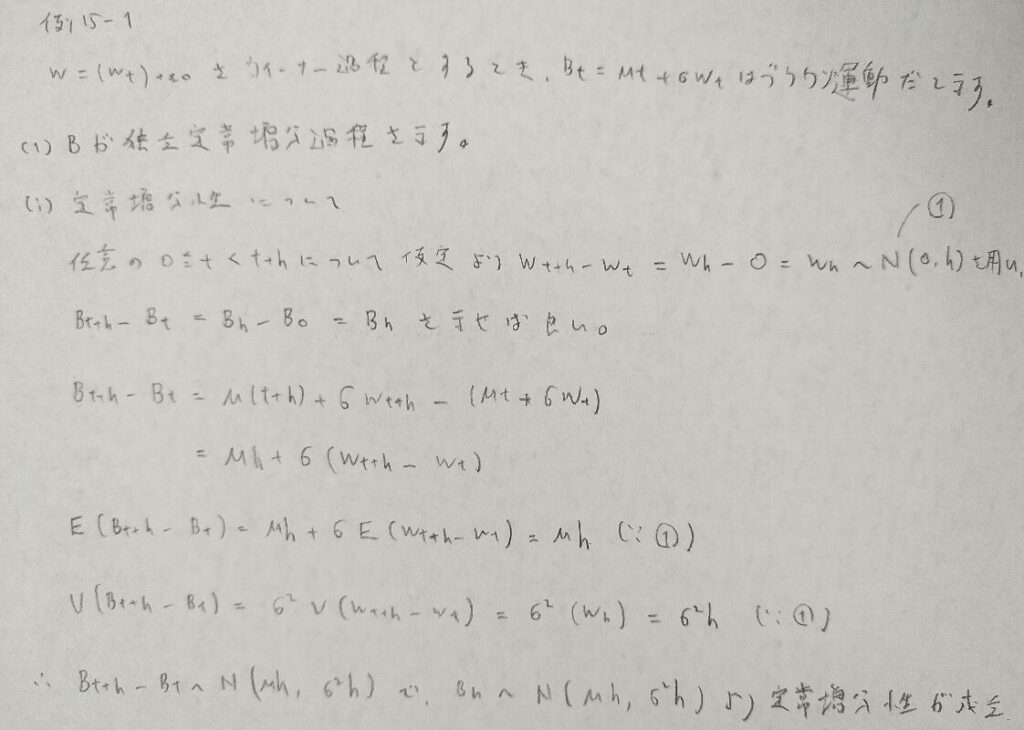

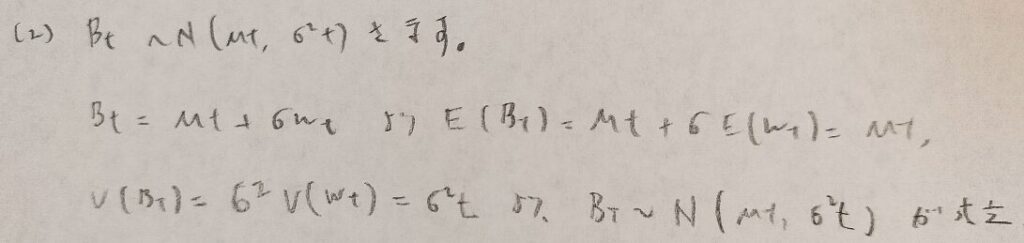

本問はウィーナー過程とブラウン運動を結びつける関係式に関する問題です。
例15−2
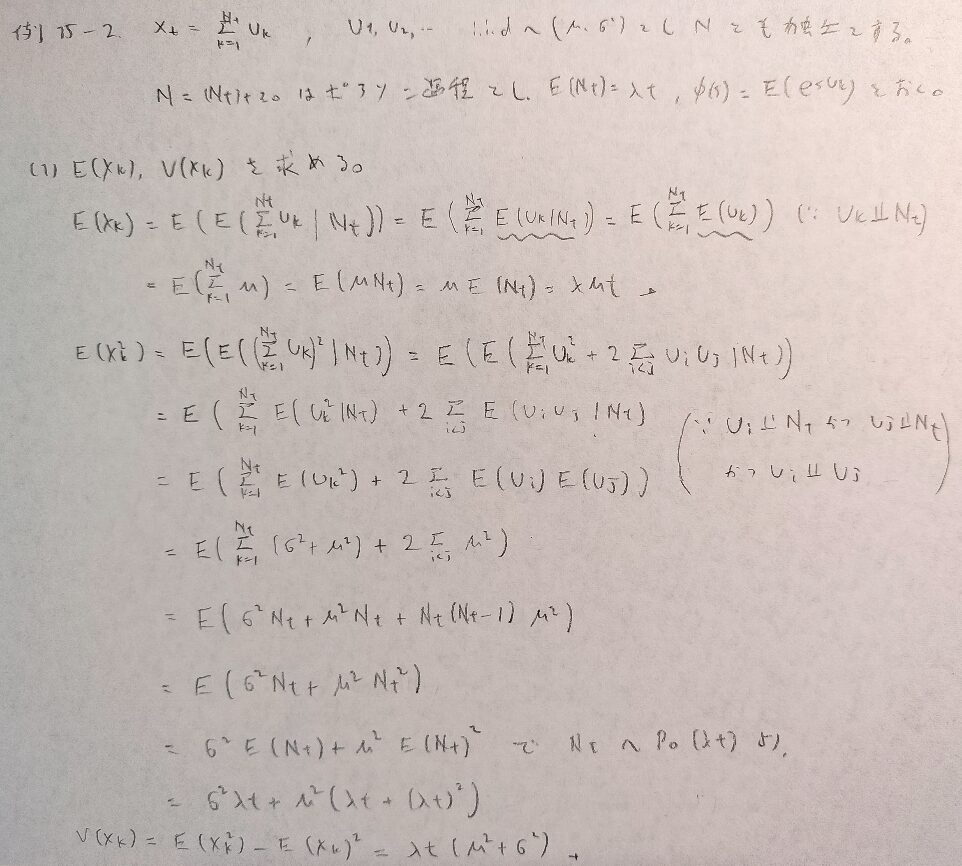
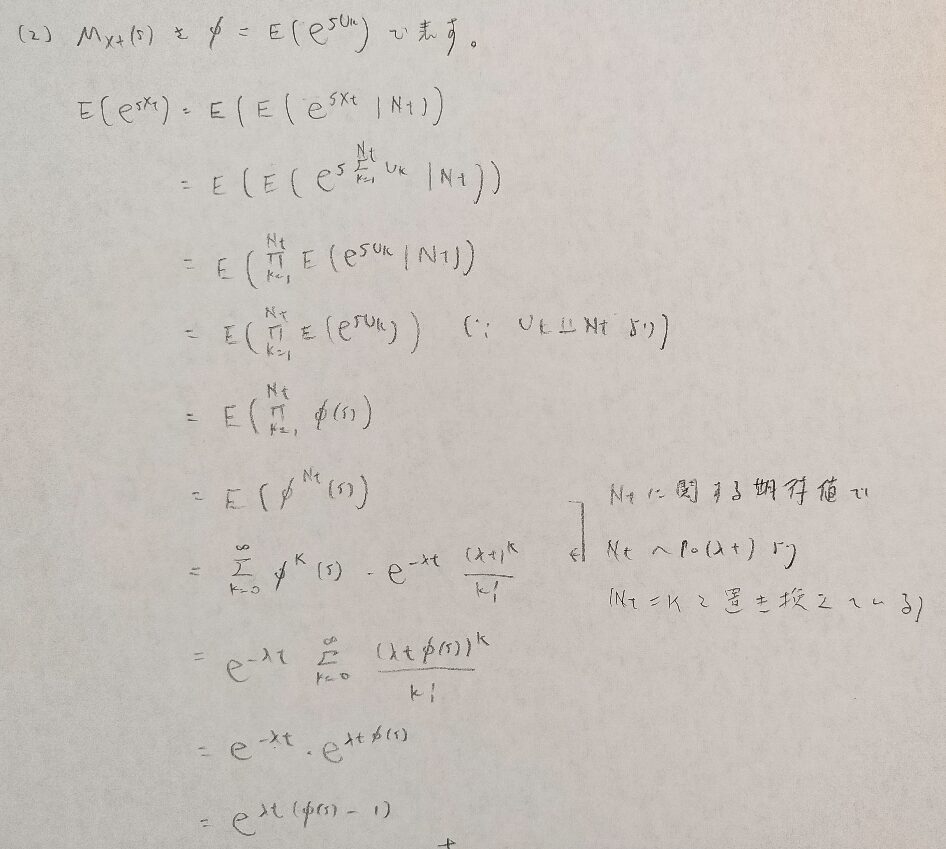
問15.1
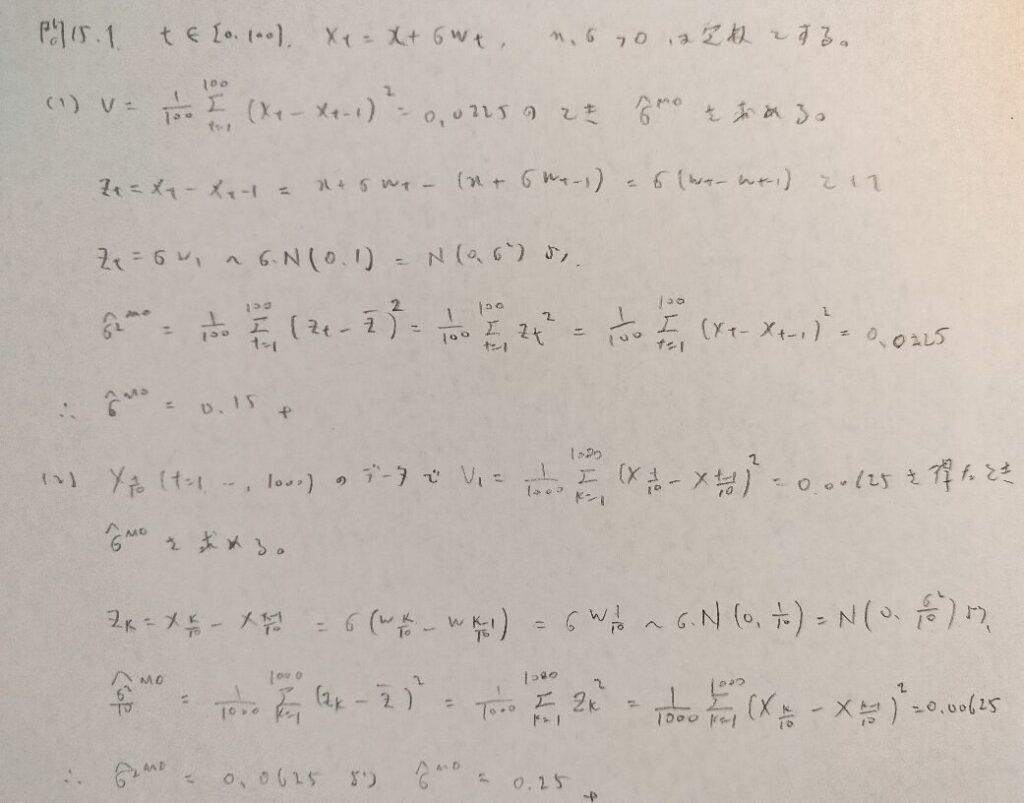
問15.2


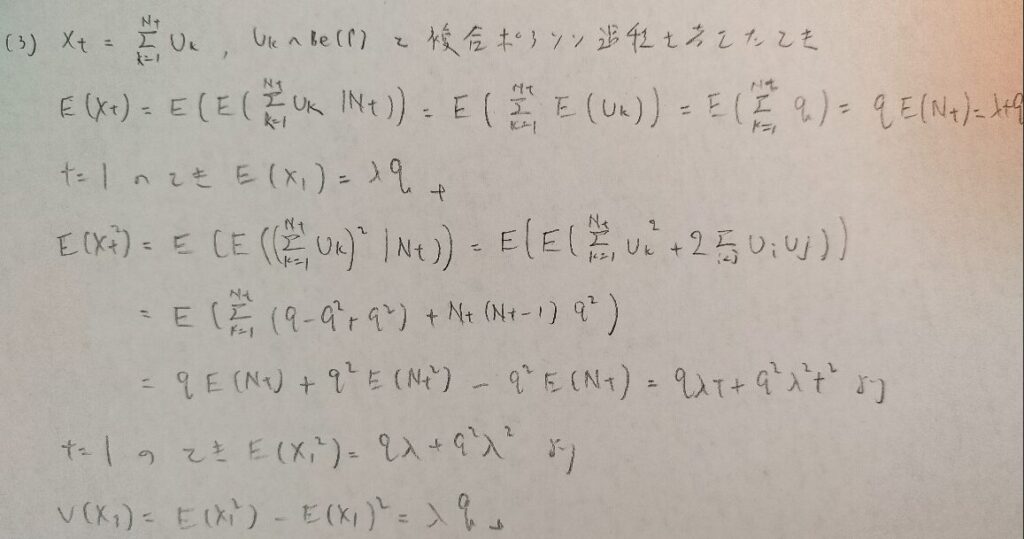
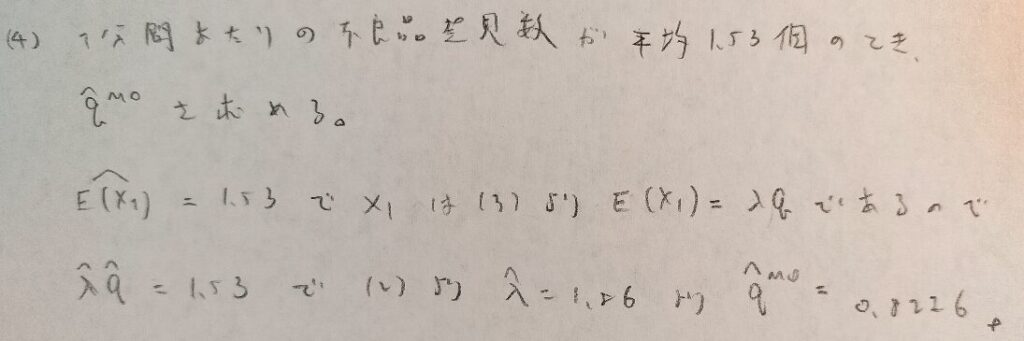
第15章メモ
本章ではブラウン運動とポアソン過程が頻出です。
ブラウン運動ではウィーナー過程の定義も合わせて覚えましょう!
ポアソン過程では条件付き期待値の計算もできるようにしておきましょう!
統計検定準1級ワークブック解説:第20章『分散分析と実験計画法』
問20.1

問20.2
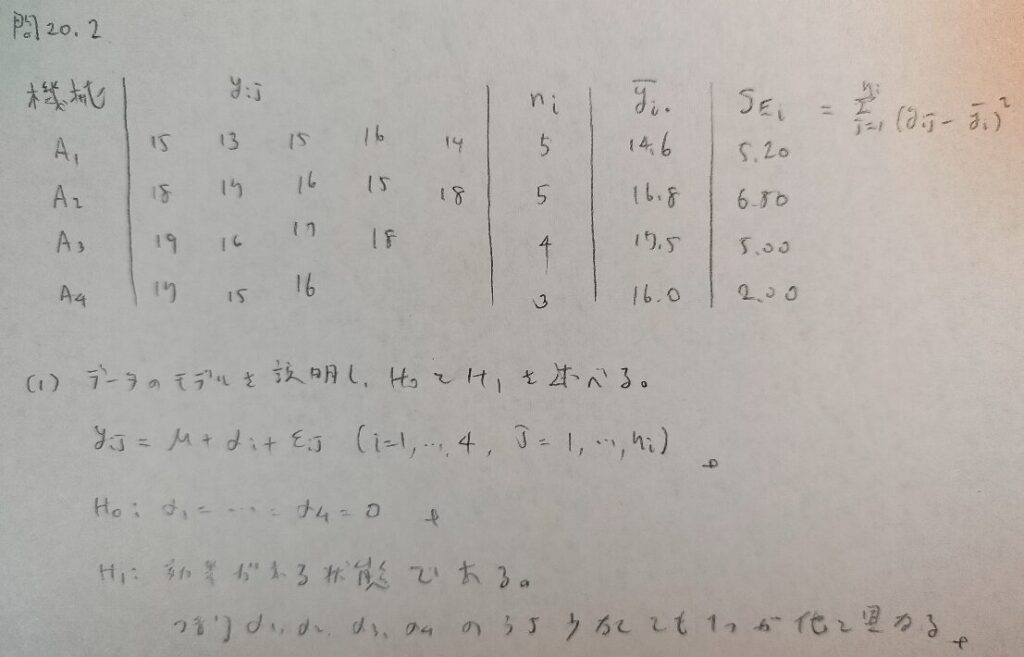

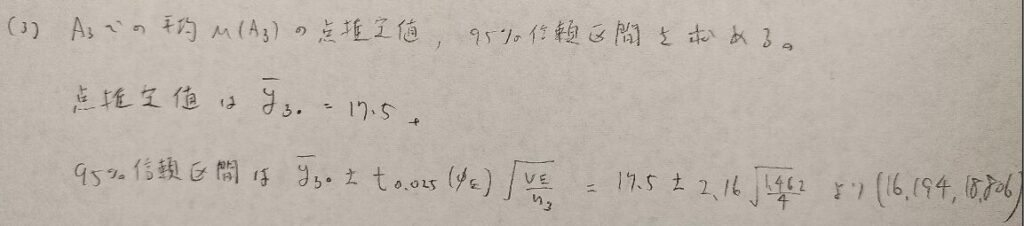
問20.3




問20.4
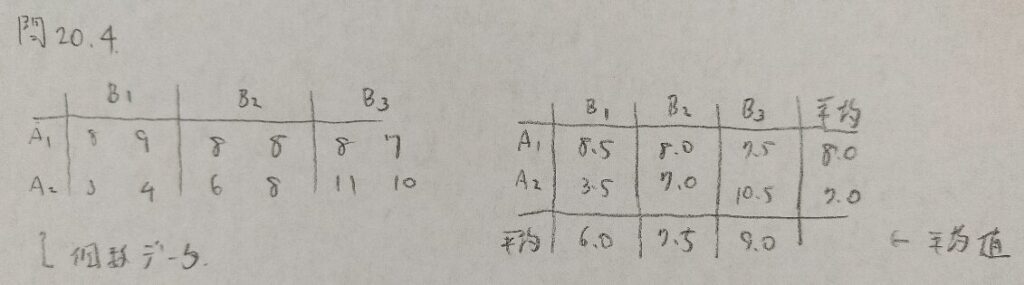

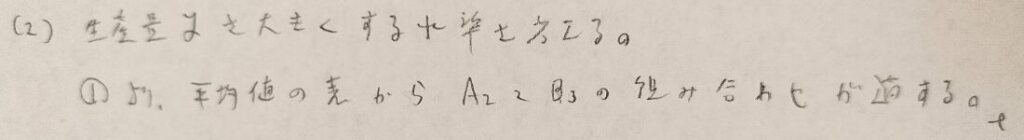
問20.5




問20.6






問20.7

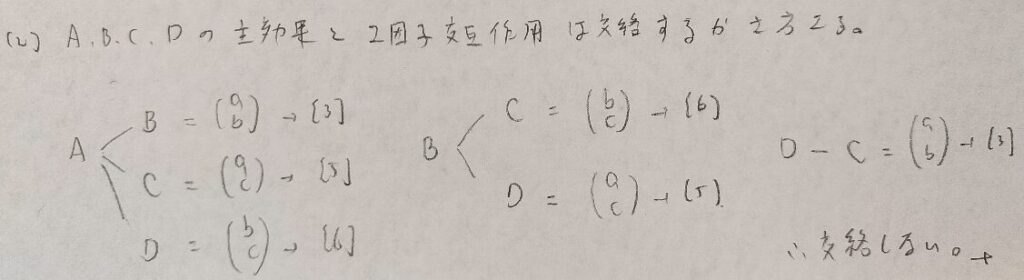

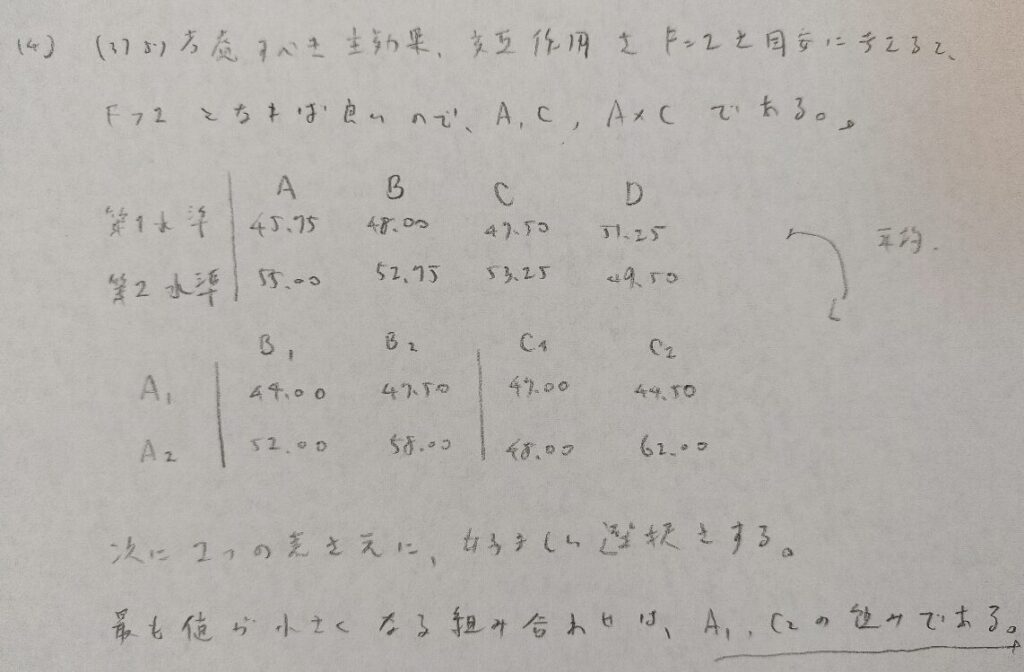
統計検定準1級ワークブック解説:第21章『標本調査法』
例21−1
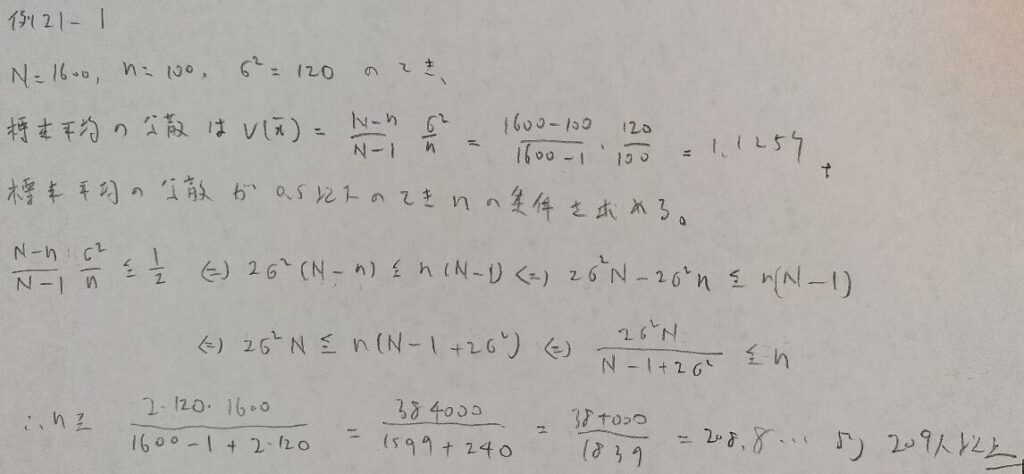
例21−2
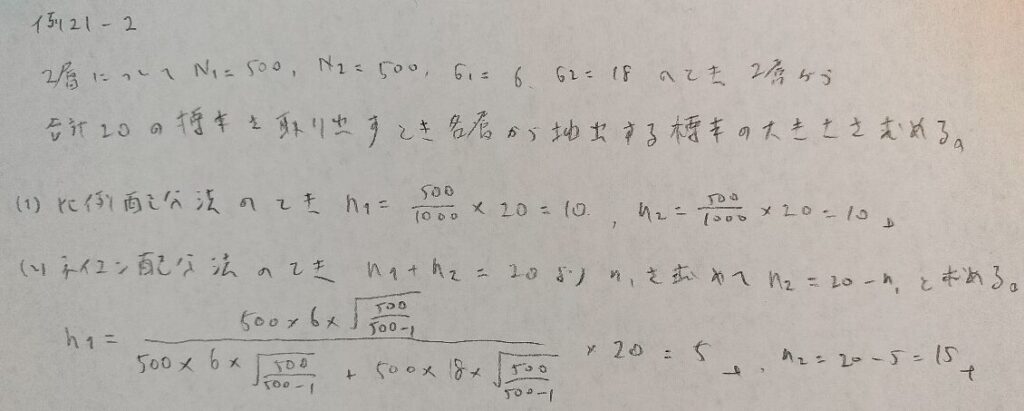
問21.1

問21.2

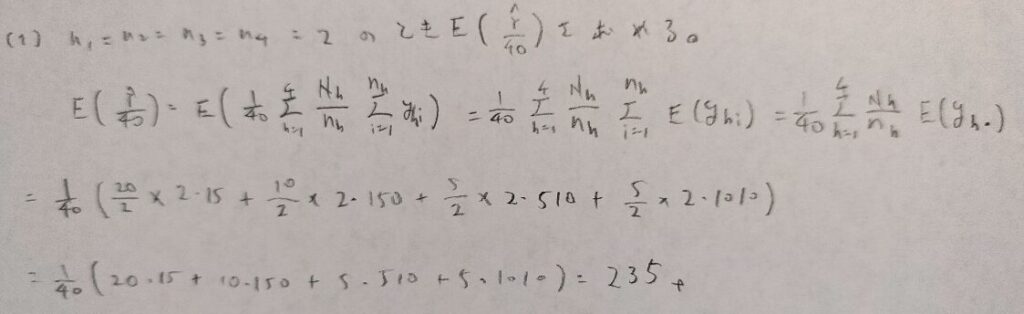
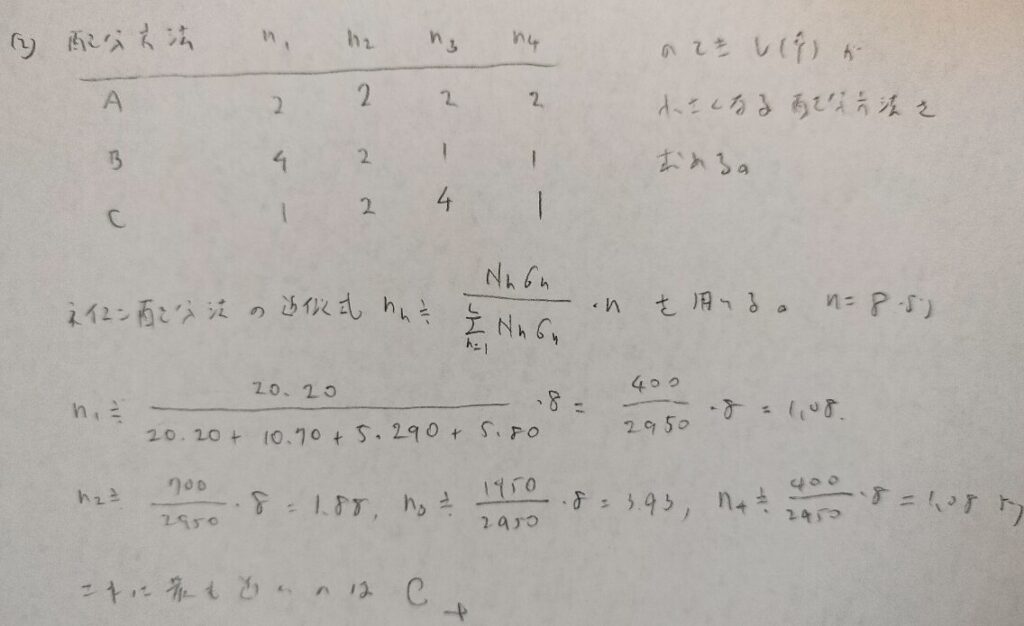
問21.3

統計検定準1級ワークブック解説:第27章『時系列解析』
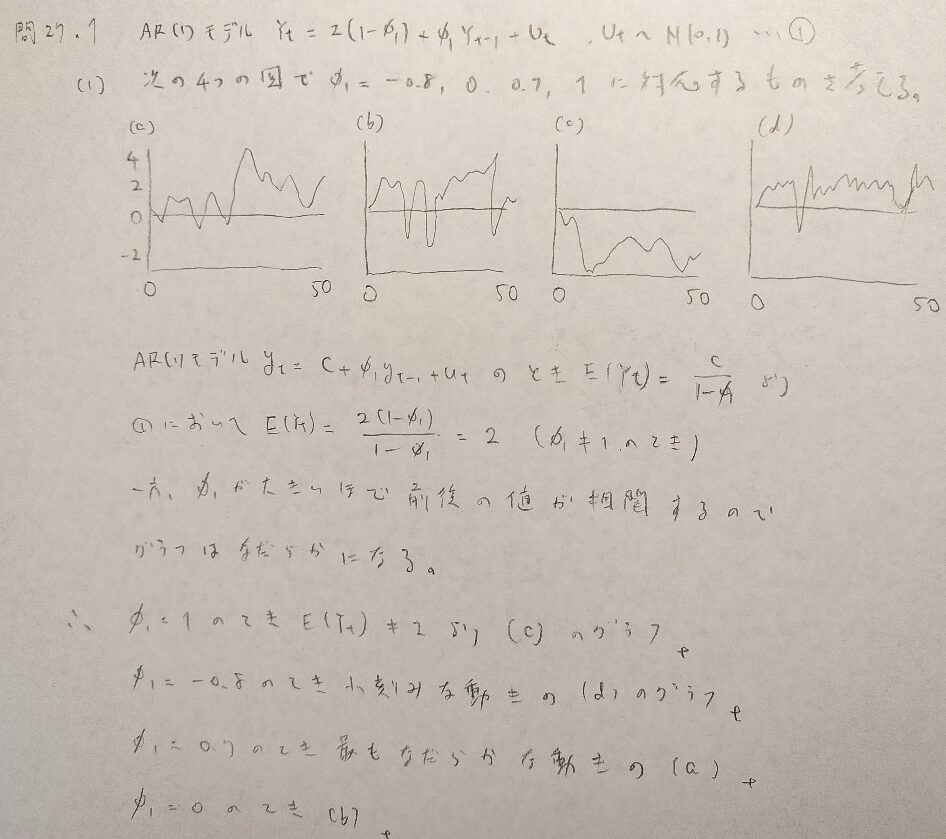
問27.1

問27.2

問27.3

問27.4

統計検定準1級ワークブック解説:第28章『分割表』
例28−1

問28.1
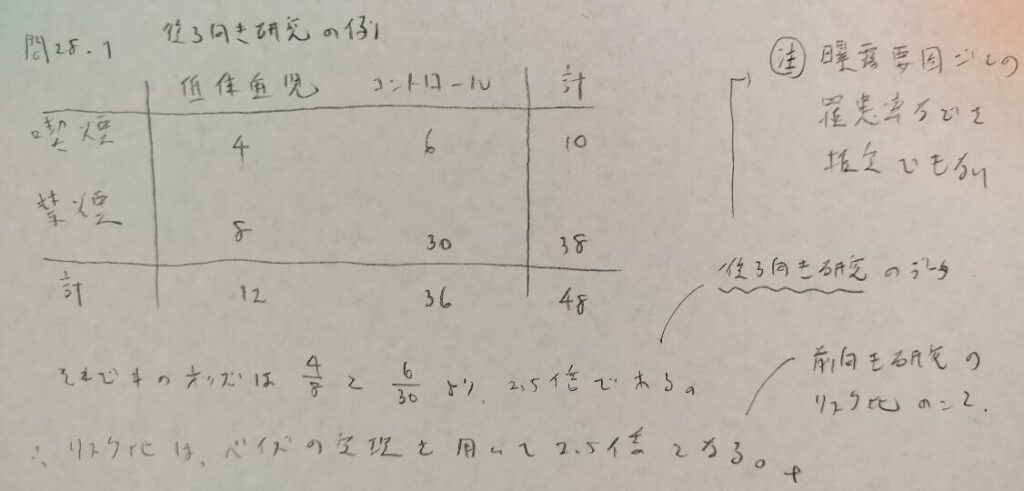
問28.2
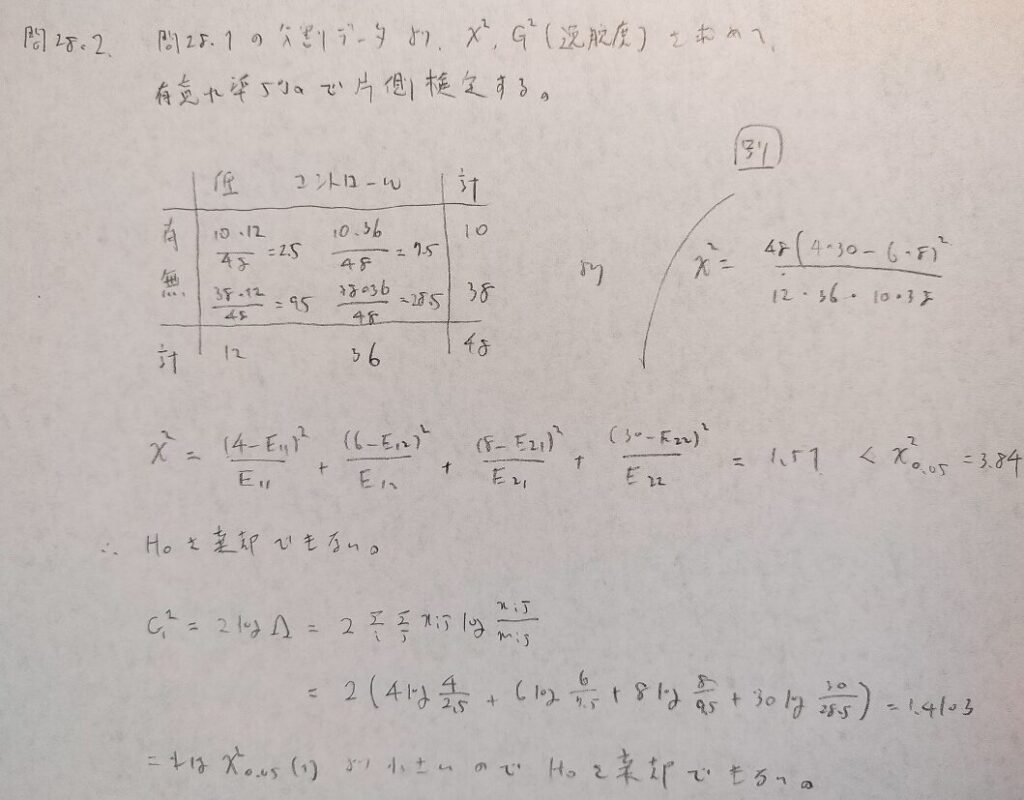

問28.3

第28章メモ
例えば問28.3の無向グラフにおいて、各因子から伸びている線は因子にくっつけた方が良いです。
記述式でない統計検定準1級の試験の時などは時間がないので上の解答のように書いても大丈夫です。
統計検定準1級ワークブック解説:第29章『不完全データの統計処理』
例29−1
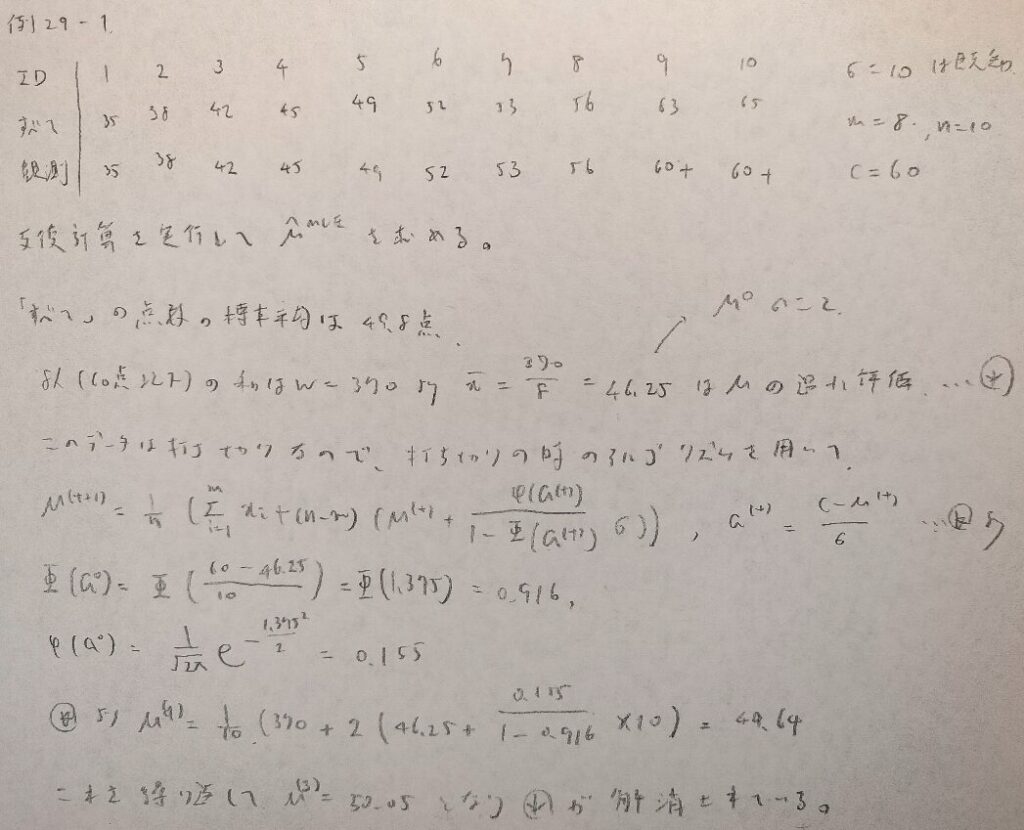
例29−2

問29.1

第29章メモ
打ち切りとトランケーションはそれぞれ母平均の推定量を求めるアルゴリズムが異なります。
データがどちらになるか?をしっかり捉えてから母平均を推測するアルゴリズムを用いましょう!
打ち切り→打ち切られたデータの数が判明しているとき
トランケーション→打ち切られたデータの数が判明していないとき
統計検定準1級ワークブック解説:第31章『ベイズ法』
例31−1
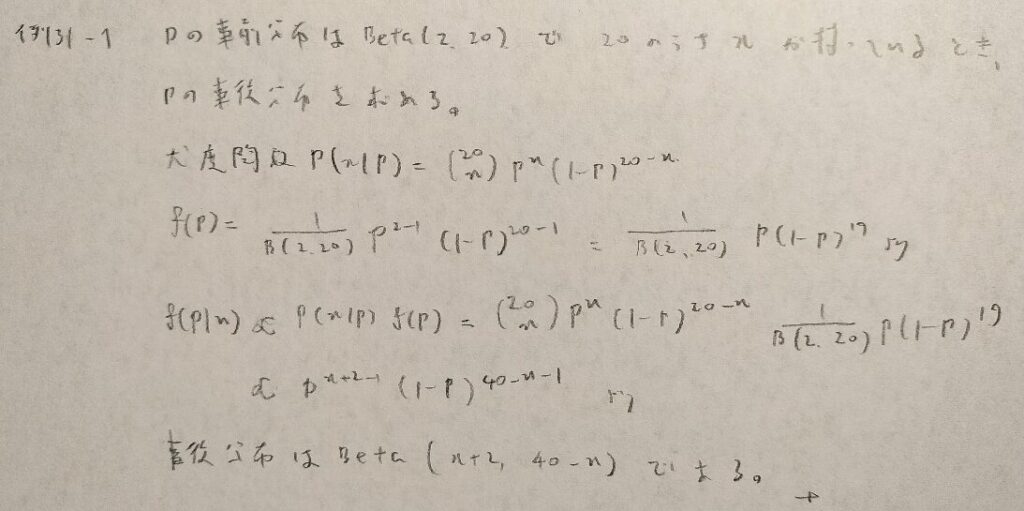
例31−2

例31−3
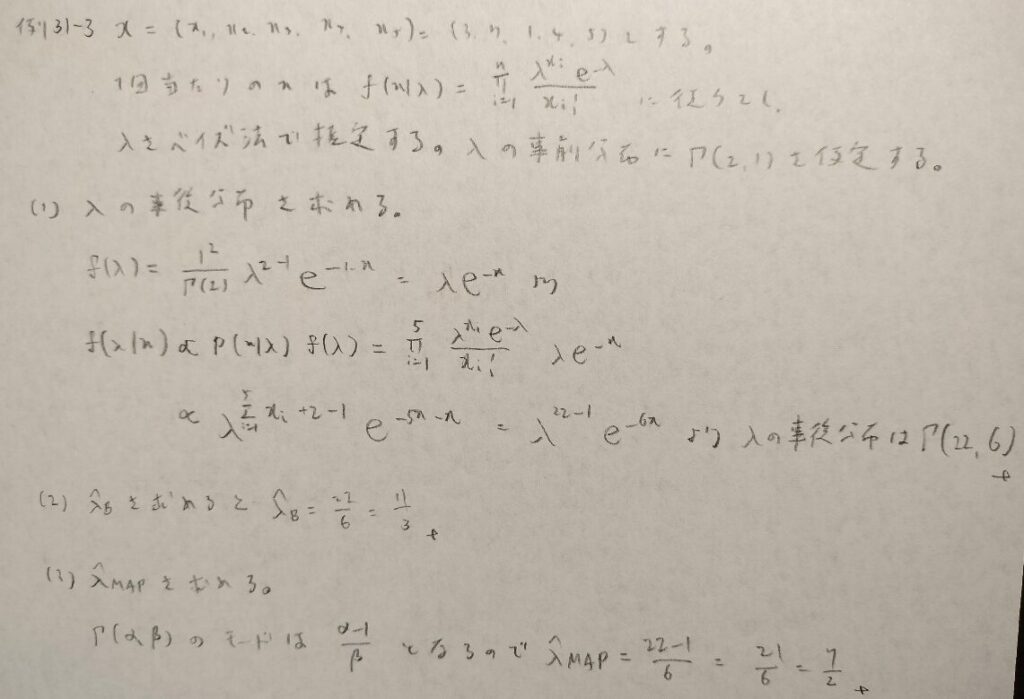
問31.1

問31.2
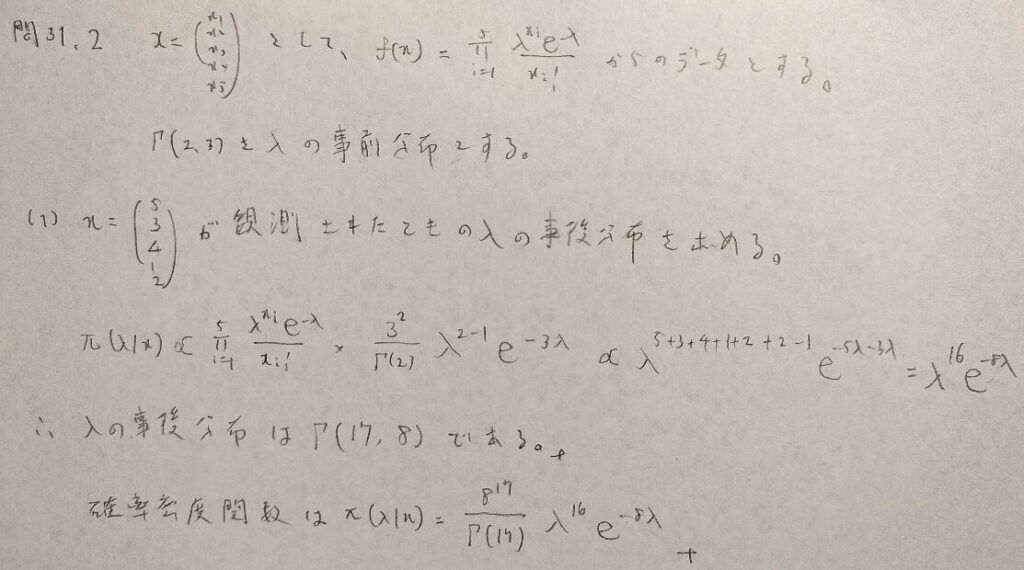
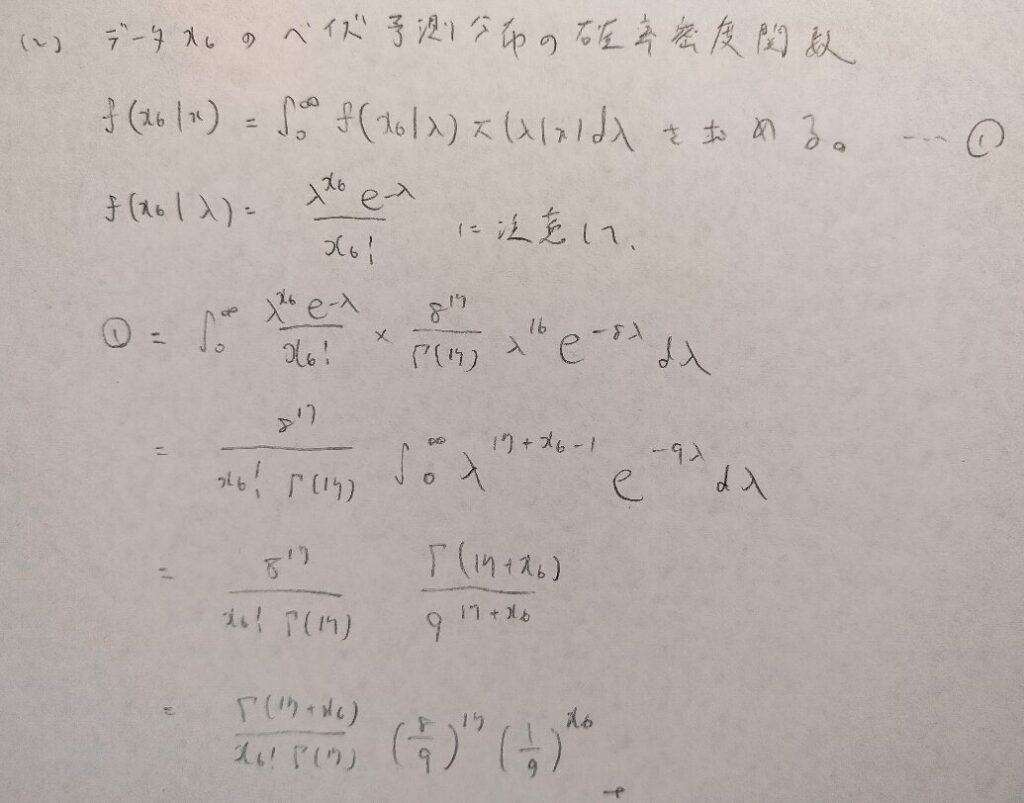
問31.3

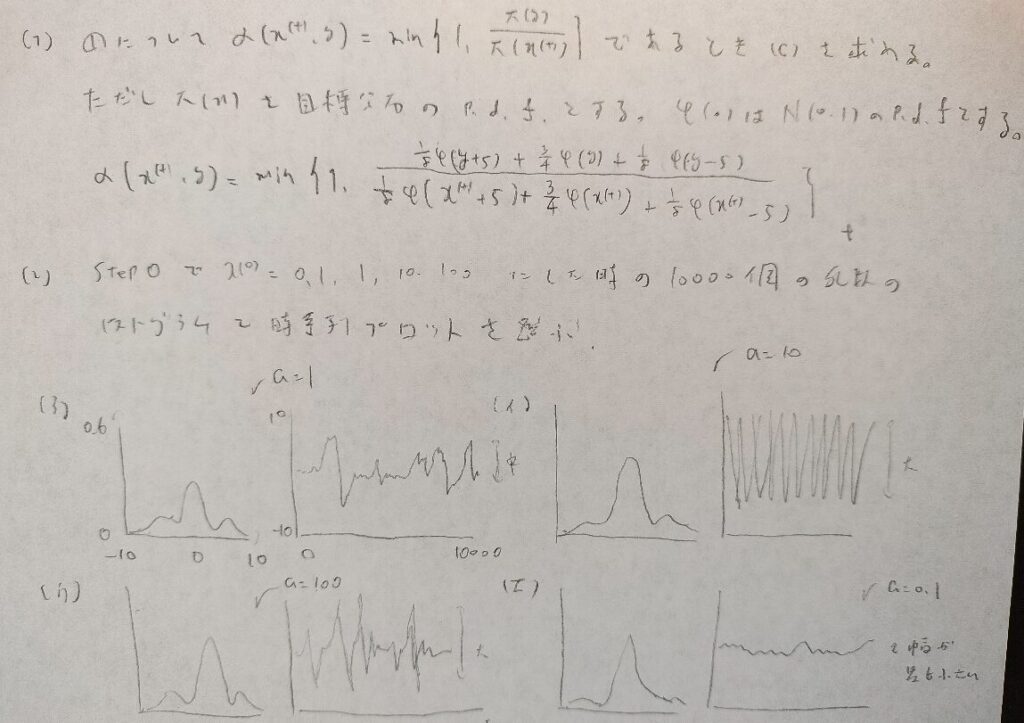

初期値が大きいとyを選択する確率が下がりやすく値が変動しにくい
初期値が小さいとyを選択する確率が上がりやすく値が変動しやすい
ただしこれらはaの値(ステップ幅に影響)による。
問31.4

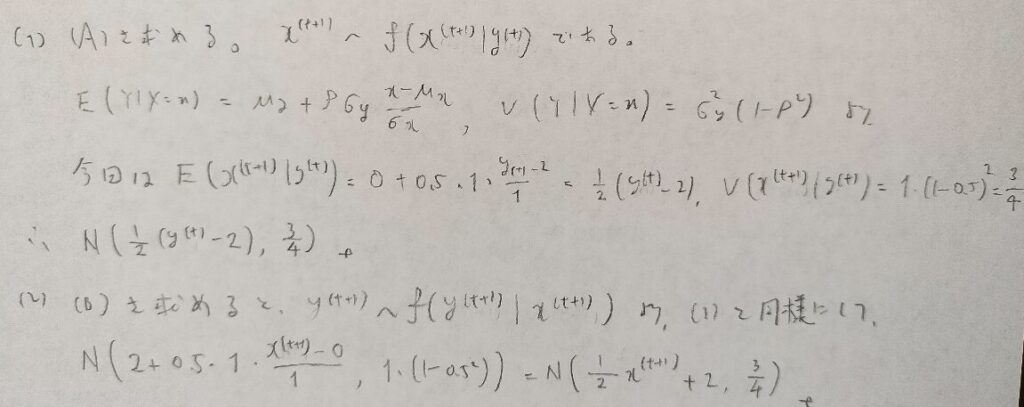
統計検定準1級ワークブック解説:第32章『シミュレーション』
例32−1

例32−2

例32−3
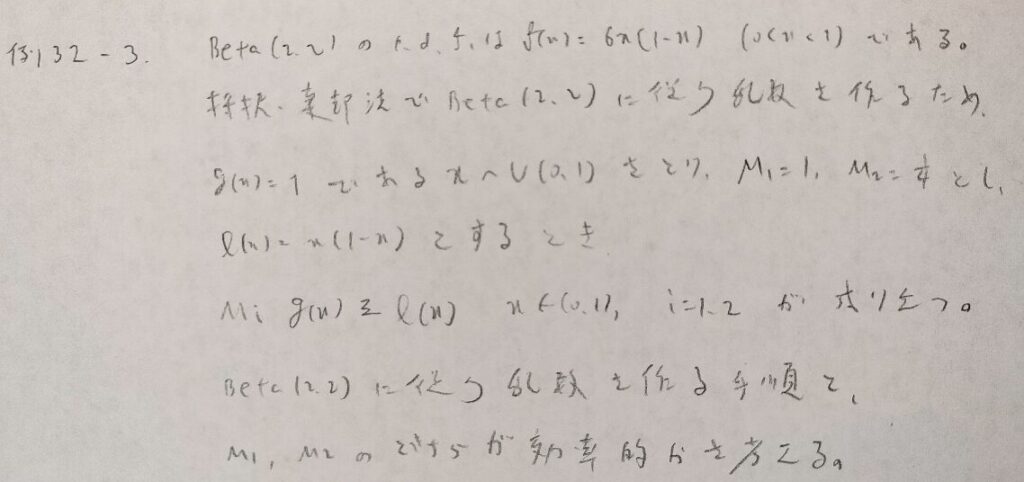

アクチュアリー数学では棄却法といいます。
例32−4

例32−5

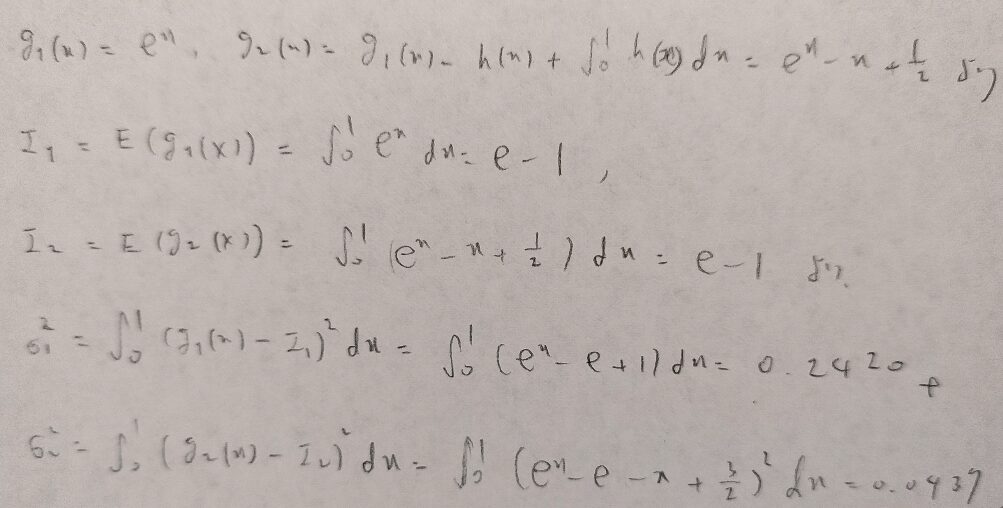
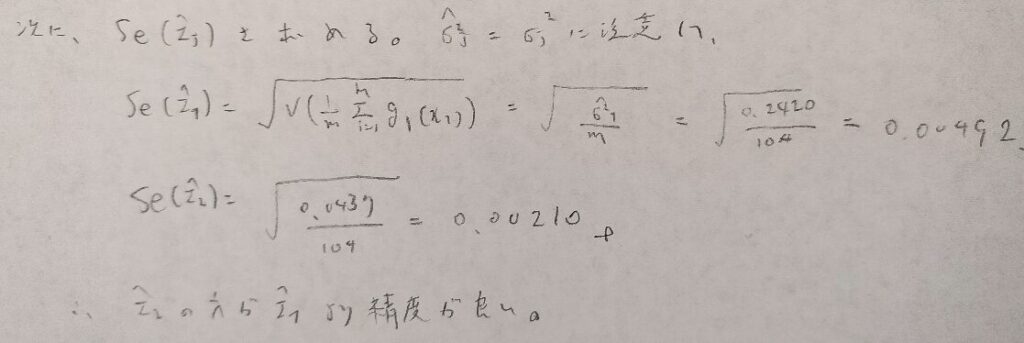
例32−6
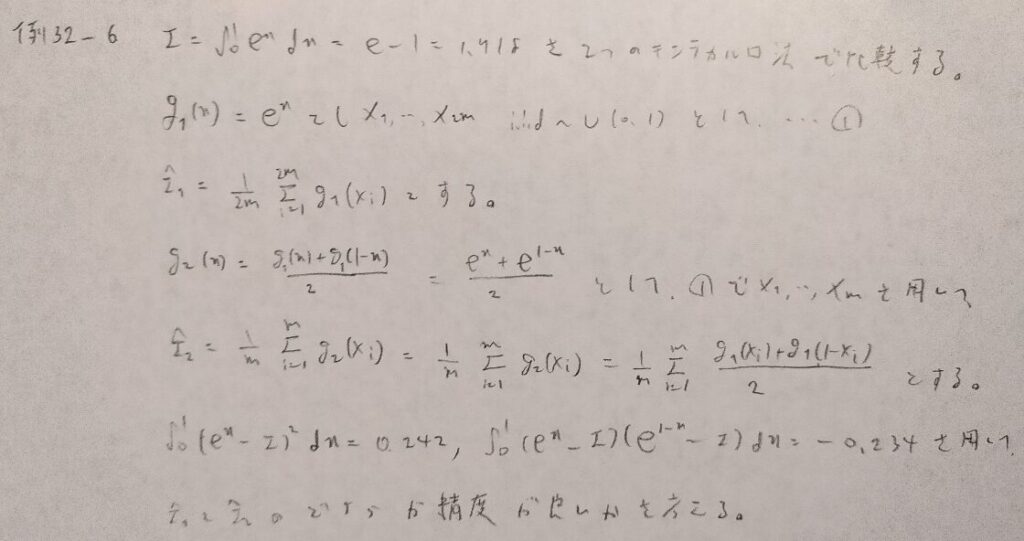
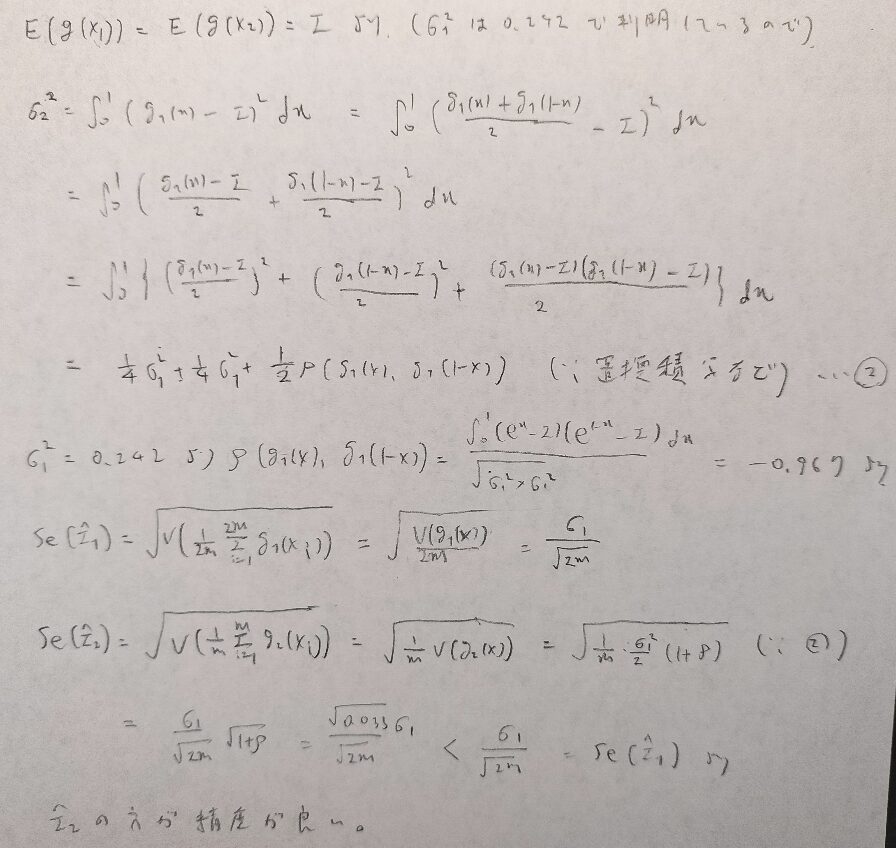
例32−7

例32−8

問32.1
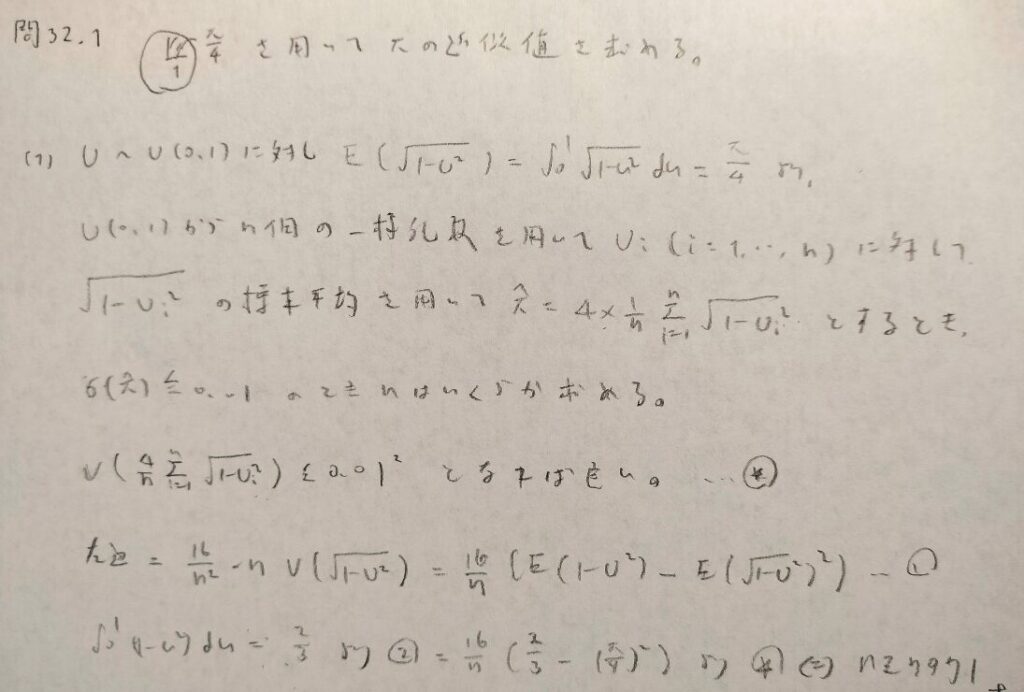
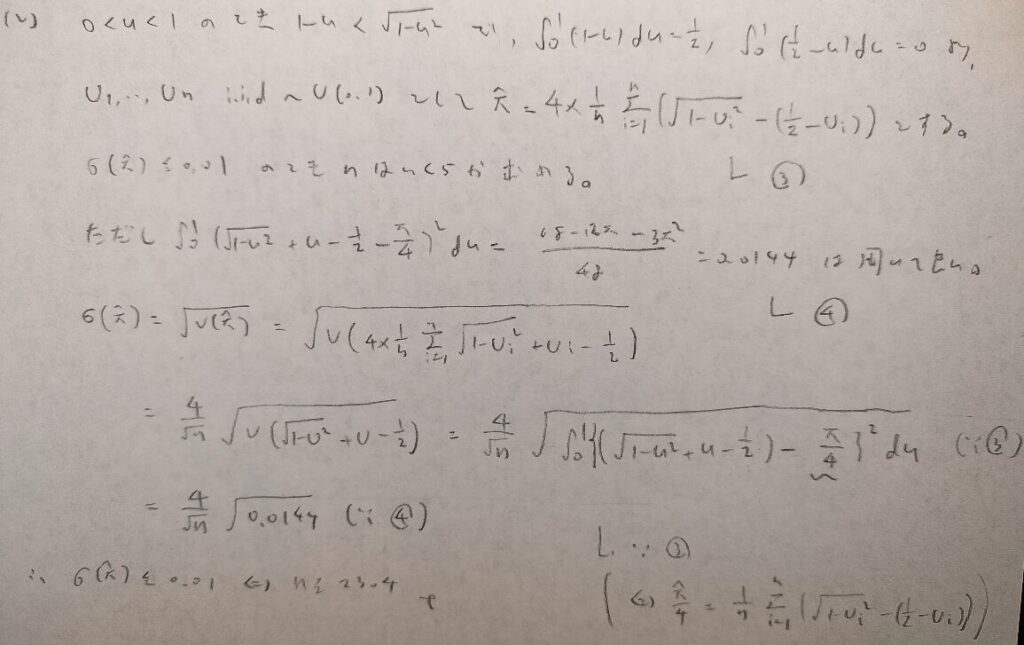
統計検定準1級ワークブック対策の第4部『種々の応用』は以上になります。
第1部から第4部までかなりの長さだったと思います。『日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック』は1周目は大変ですが2周目以降の復習は高速化できると合格者の方々は口を揃えて言っています。ワークブックの4つの記事を一緒に復習をしていきましょう!
統計検定準1級ワークブック第1部→確率と確率分布
統計検定準1級ワークブック第2部→統計的推測
統計検定準1級ワークブック第3部→多変量解析法
統計検定準1級のバイブルとして定着している準1専用書です。1章1章が1冊の本になりうる内容が全部で32章あり、統計学のベースとなる知識がこれ1冊で手に入ります。

