統計検定準1級対策として『日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック』を用いた学習の中でもボリューミーな「多変量解析法」を第3部として扱います。
これまで統計検定準1級のため用いているワークブック対策での第1部と第2部はそれぞれ次の記事で紹介しています。
統計検定準1級ワークブック第1部→確率と確率分布
統計検定準1級ワークブック第2部→統計的推測
統計検定準1級ワークブック第3部→多変量解析法
統計検定準1級ワークブック第4部→種々の応用
次はいよいよ統計検定準1級で初登場となるテーマ揃いの多変量解析編です!
多変量解析は永田先生の『多変量解析法入門』が最もわかりやすくおすすめです。このブログの多変量解析の記事も永田先生の著作を参考にしながら解説しています。
第4部として考えている「種々の応用」に該当すると思った部分は後回しにしています。そのため第3部「多変量解析法」の章は飛び飛びになっているところが多々あります。目次をご参照くだされば幸いです。
統計検定準1級ワークブック解説:第16章『重回帰分析』
ワークブックの重回帰分析の部分は難解に書かれているので、永田先生の『多変量解析法入門』を参考にするのがおすすめです!
単回帰分析と重回帰分析の記事は別に書いていますので、そちらをご覧になってからの方が理解しやすいです。
問16.1

問16.2

問16.3


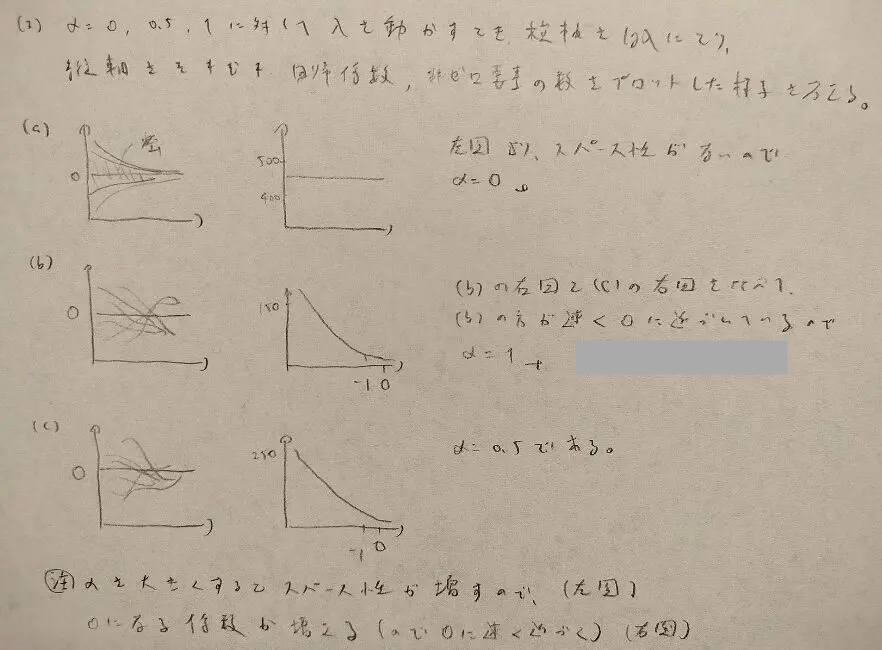
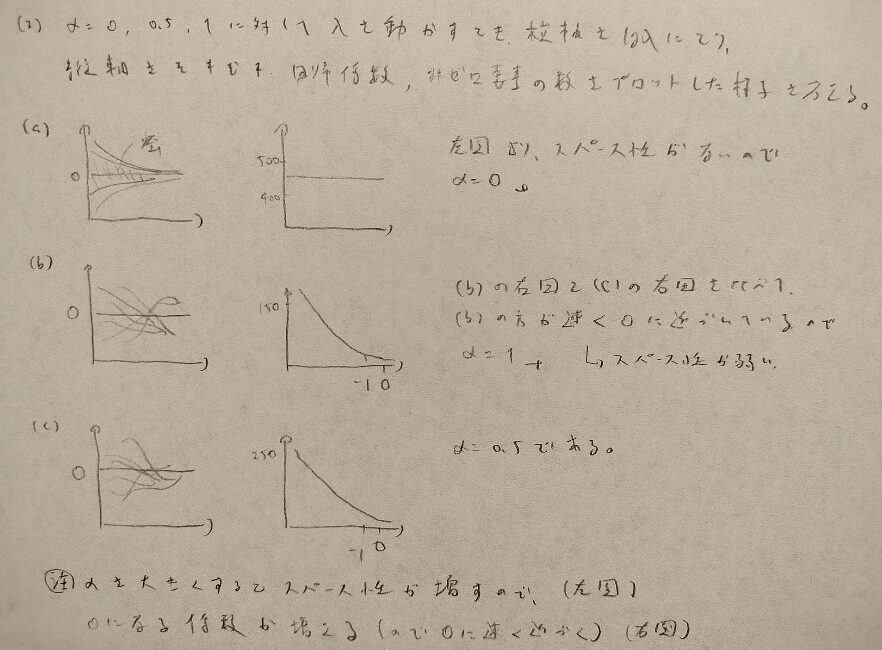
第16章メモ
統計検定準1級ではモデルの説明力・モデルの有意性・正則化が大事です。
モデルの説明力→自由度調整済み決定係数
モデルの有意性→F検定すなわち偏回帰係数の検定
正則化→リッジ回帰とラッソ回帰(スパース性あり)です。
Lasso回帰→L1正則
Ridge回帰→L2正則
覚え方はLが1に見えて、Rが2に見えるからだと覚えましたが…こじつけです笑
スパース性についてαを大きくするとβ(解)はスパース(疎)になるので、0になる係数が増えます(問16.3参考です)
統計検定準1級ワークブック解説:第17章『回帰診断法』
例17−1




問17.1
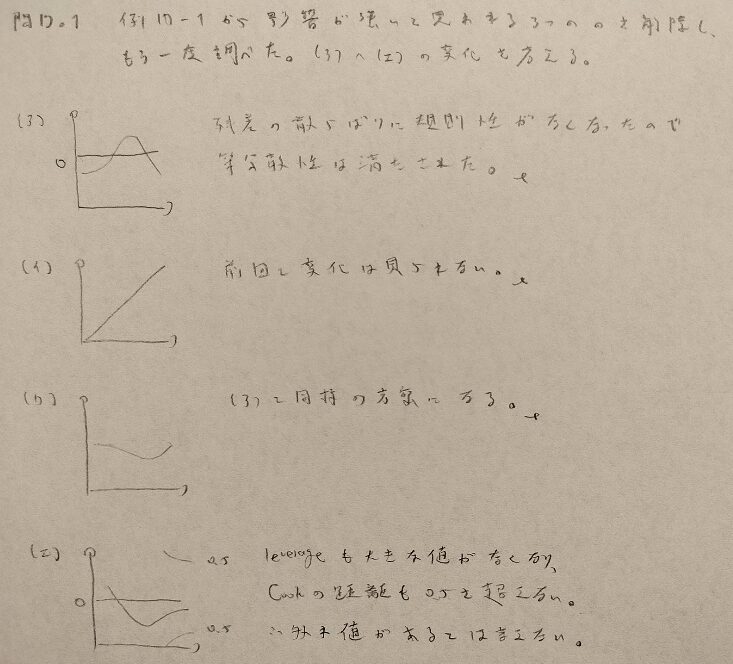
第17章メモ
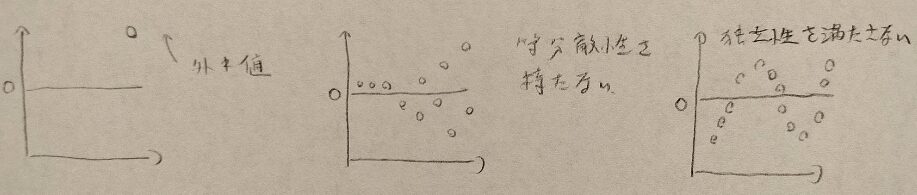
等分散性を持たないときは振幅が増大していくイメージのプロットになりますね。
残差の独立性を知るためには次のような時系列解析で用いるDW比もあります。
DW比については0〜4の値をとり、
0に近づくと自己相関あり。
2に近づくと自己相関なし。
4に近づくと負の自己相関あり。
統計検定準1級ワークブック解説:第18章『質的回帰』
この章ではロジスティック回帰モデル・プロビットモデル・ポアソン回帰モデルを学習します。
それぞれの回帰モデルは別記事にて詳しくまとめていますので、まずはそちらをご覧になることをおすすめします!また推定値の式を考える際は^を忘れずにつけましょう!
問18.1
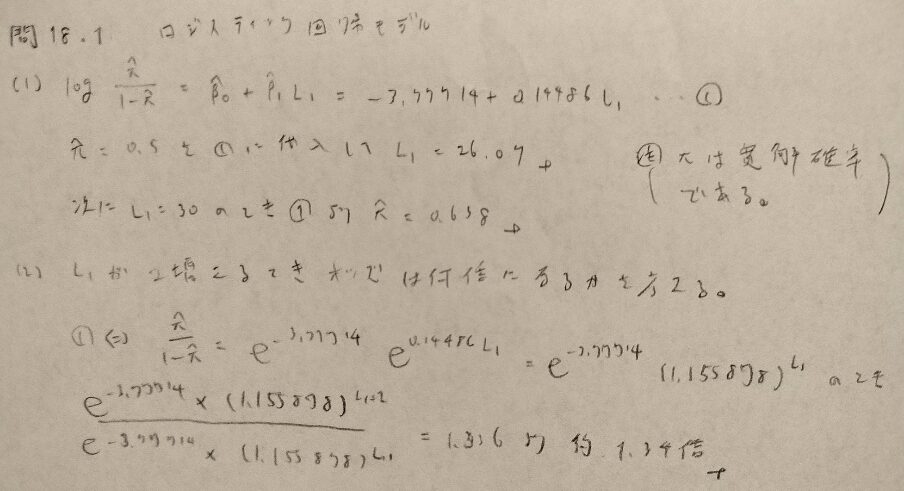
問18.2

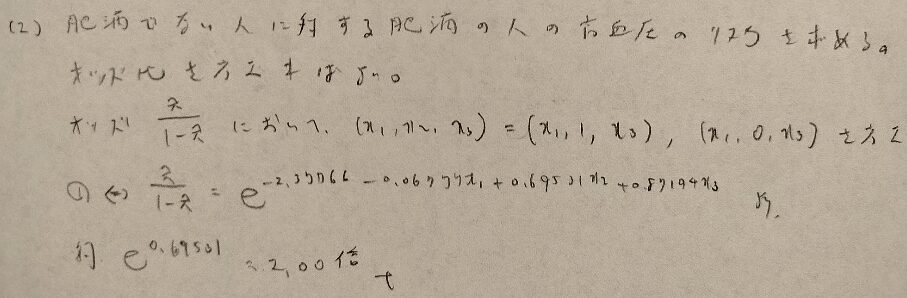

問18.3
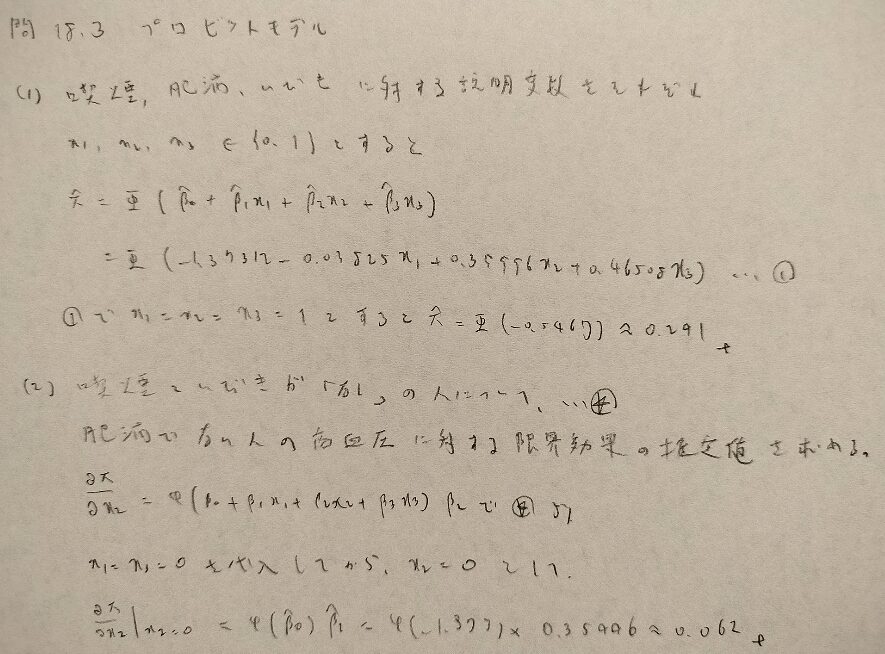
問18.4

第18章メモ
本章ではロジスティック回帰モデル・プロビットモデル・ポアソン回帰モデルを学習しました。
問題にもありましたが、それぞれ次のような対応関係があります。
ある変数に注目してそれ以外を固定して考えるとき、
ロジスティック回帰モデル→オッズ比(でリスクを求める)
プロビットモデル→限界効果
ポアソン回帰モデル→対象の変数を底をeとする指数関数をとる。
統計検定準1級ワークブック解説:第19章『回帰分析その他』
例19−1
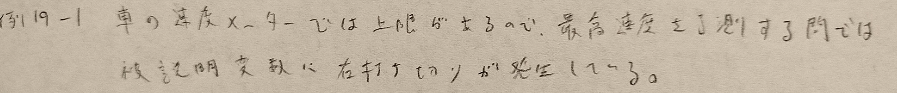
例19−2

例19−3

問19.1
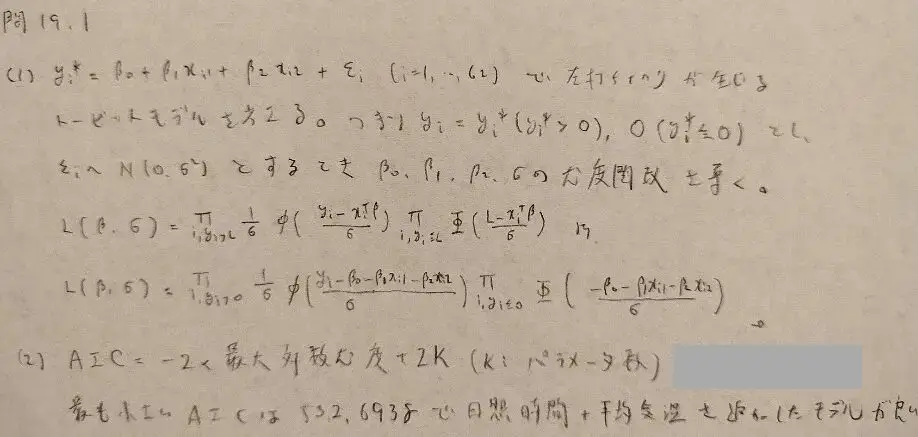
問19.2
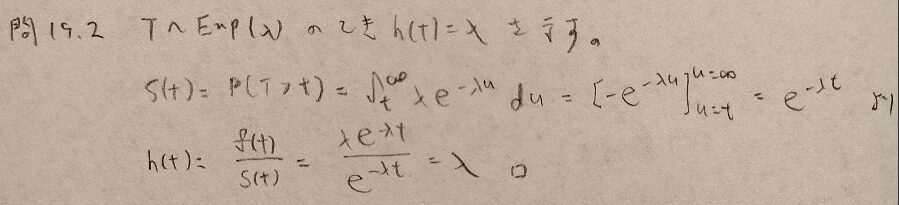
問19.3
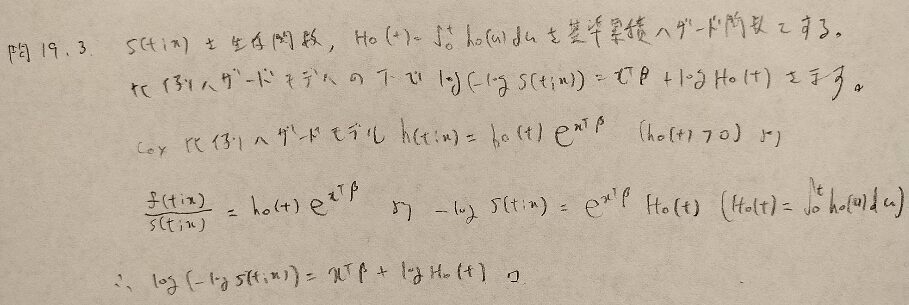
問19.4

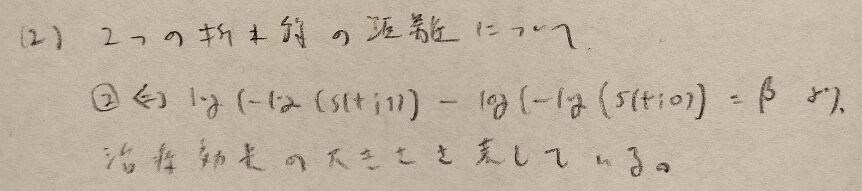
第19章メモ
ハザード関数で代表的な4つのモデルについて解説します。
①指数分布→定数
②ワイブル分布(p>1)→単調増加
③ワイブル分布(p<1)→単調減少
④対数正規分布→増加後減少
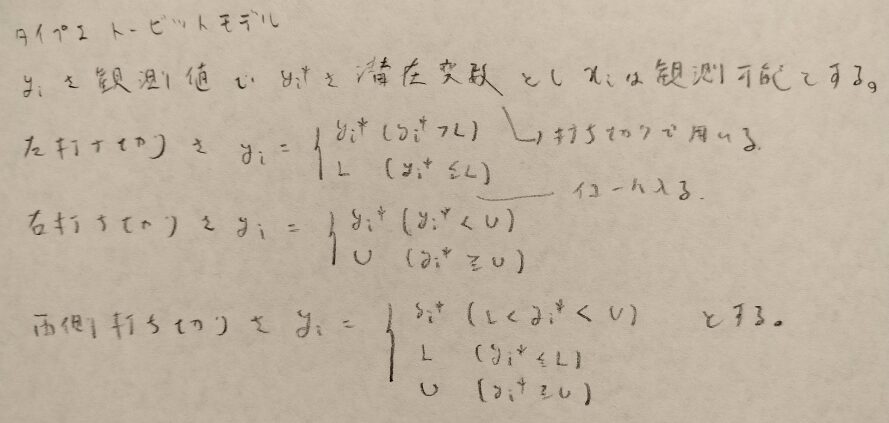
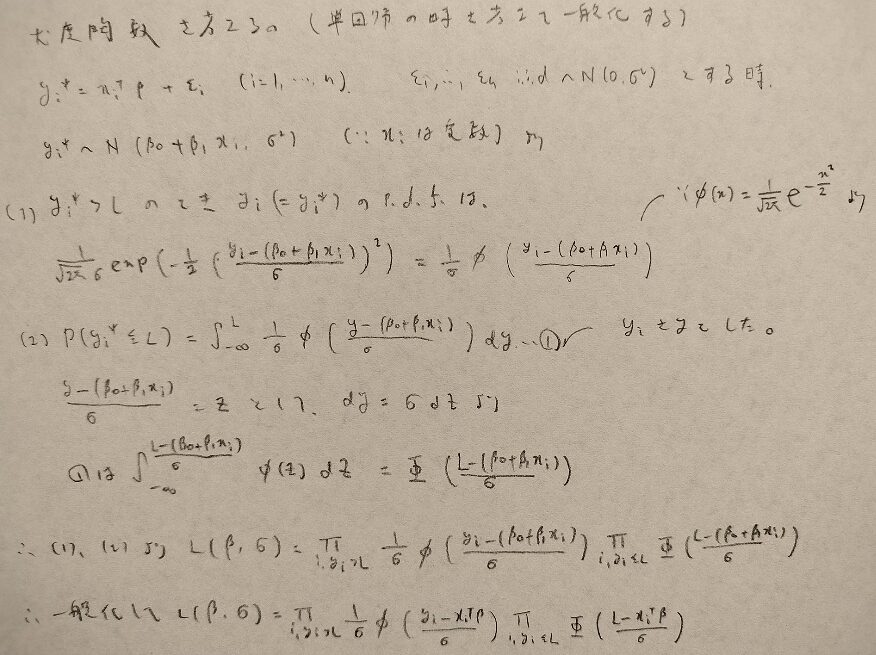



入力層と出力層の間にある層を中間層や隠れ層といいます。
中間層が増えるのは合成回数が増えるためです。
中間層が多いニューラルネットワークを深層ニューラルネットワークといいます。
統計検定準1級ワークブック解説:第22章『主成分分析』
主成分分析については別記事にて詳しい解説を載せています。
その記事をお読みになってからワークブックの問題を解いてみましょう!
主成分分析の記事はこちらです!
例22−1
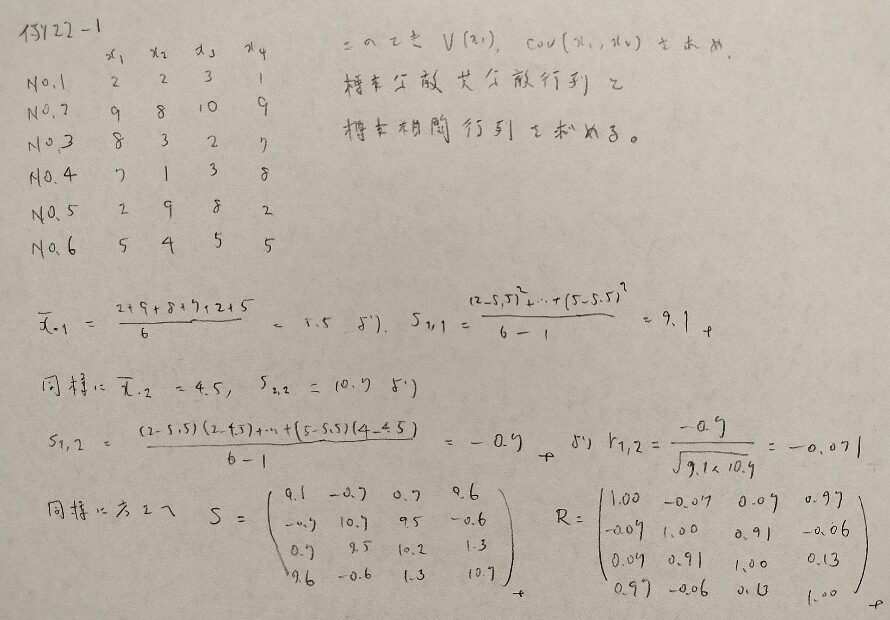
例22−2
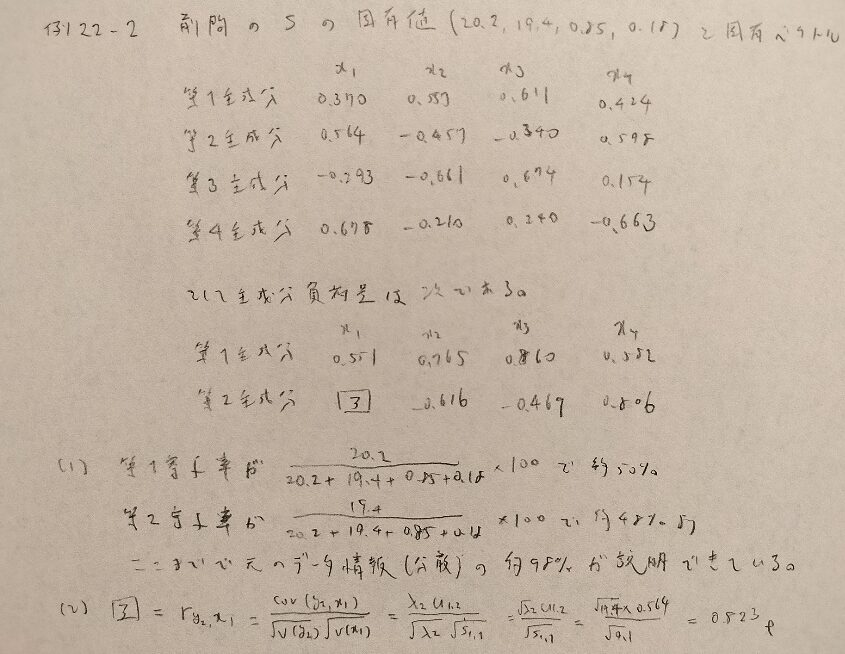
yとは主成分のことです。
問22.1



第22章メモ
主成分得点を求める際は通常のxをそのまま代入する方法と、xを中心化(各成分から平均値を引く)してから代入する2パターンがあります。
主成分分析の大まかな流れをまとめておきます。
①元データxを確認する。
②SやRを求める。
③Rの固有値と固有ベクトルを求める。
④第p主成分をxと固有ベクトルの第p列との内積で考える。
⑤寄与率の意味を確認する。
⑥主成分負荷量を求めるが2通りの求め方があるので注意です。
⑦主成分得点を求めるが2通りの求め方があるので注意です。
⑧結果の解釈を行います。
ワークブックの問題はこの流れのどこかの部分にて作られている印象ですね!
統計検定準1級ワークブック解説:第23章『判別分析』
判別分析の記事についてはこちらで詳しく解説しています。
判別分析の内容を理解してからワークブックの問題に取り組みましょう!
問23.1

問23.2
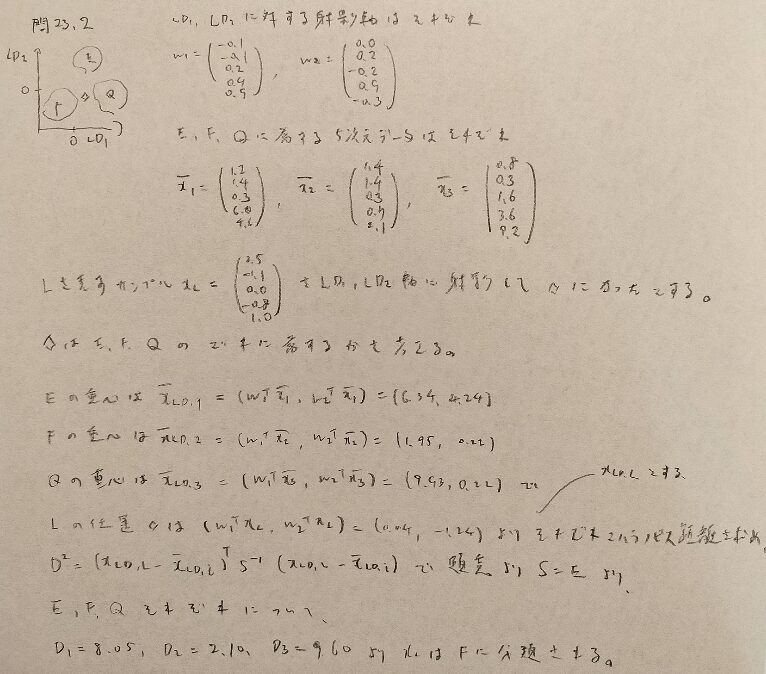
問23.3
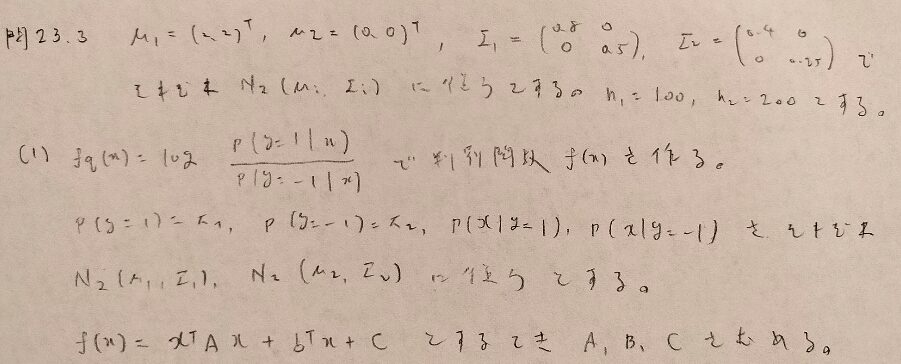
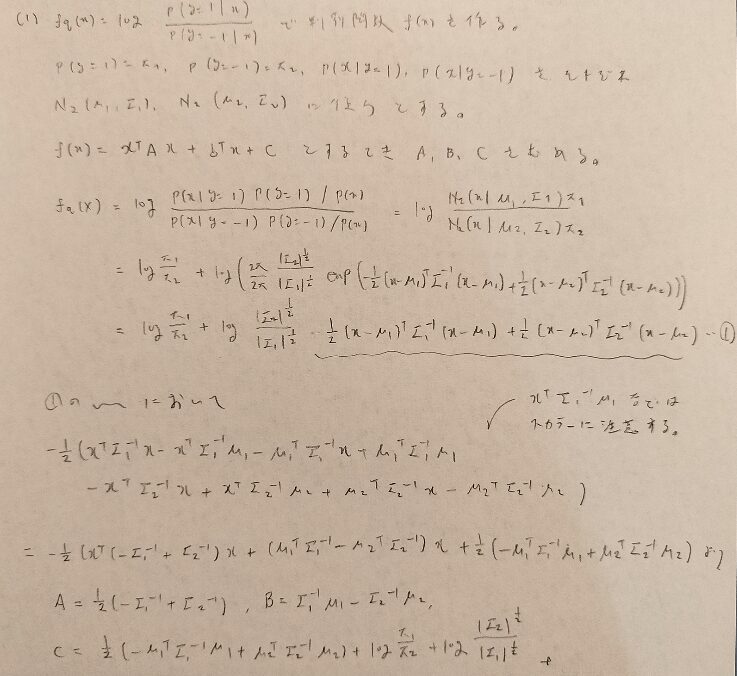
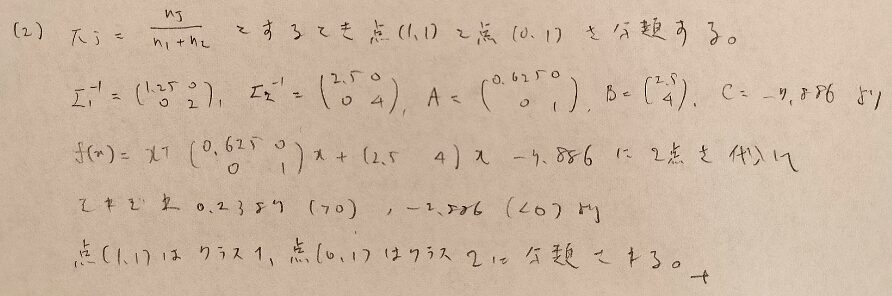
第23章メモ
ボリューミーな章ですがマハラノビス距離に基づいた判別式を考えることがポイントになります。
統計検定準1級ワークブック解説:第24章『クラスター分析』
クラスター分析について別記事に詳しく内容を紹介しています!
まずはクラスター分析の記事を読んでからの方がワークブックの問題が解きやすいと思います。
問24.1
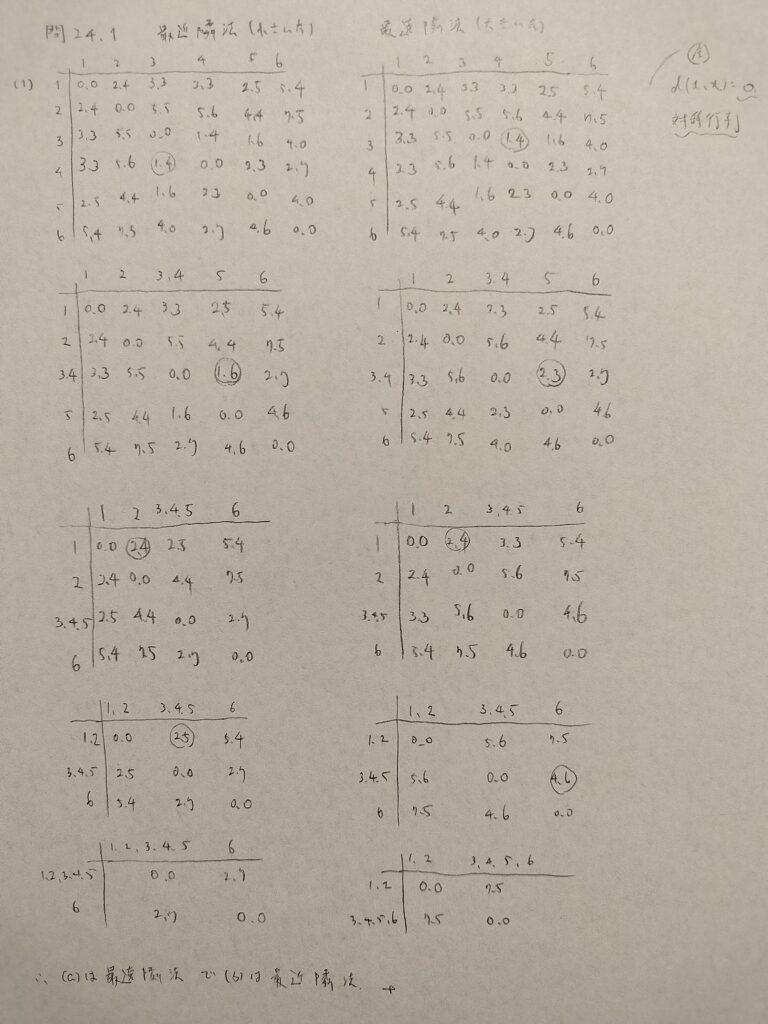

第24章メモ
クラスター分析ではクラスター間の距離をどのように定めるのか?について意識をすればわかりやすいです。
問題24であった他にも重心法・群平均法・ウォード法などがあります。
K-means法とはK個のクラスターに分類するためのアルゴリズムで、次の①と②を割り当てクラスターが変化しなくなるまで繰り返します。
①クラスター中心の更新
②クラスター割り当ての更新
統計検定準1級ワークブック解説:第25章『因子分析・グラフィカルモデル』
例25−1

例25−2
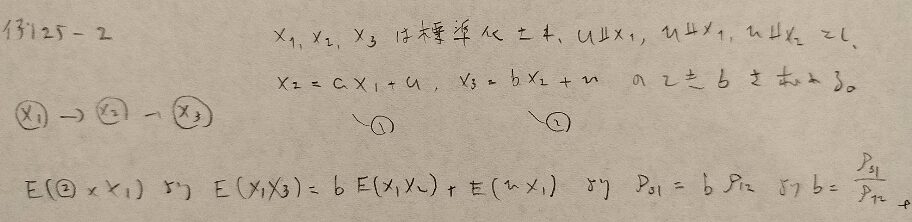
問25.1


問25.2
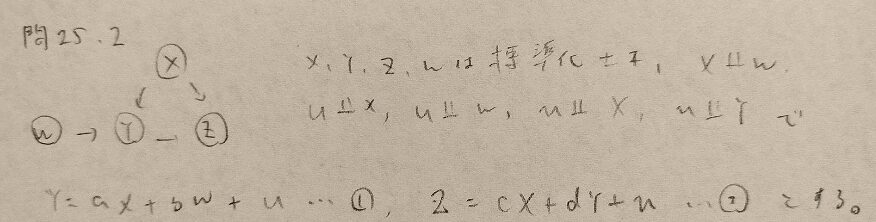
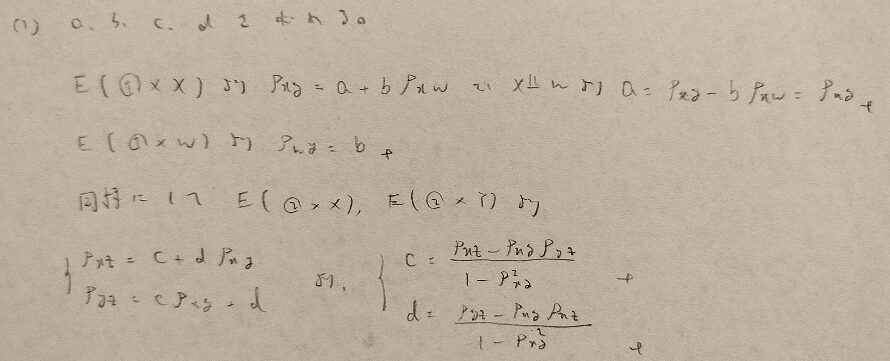
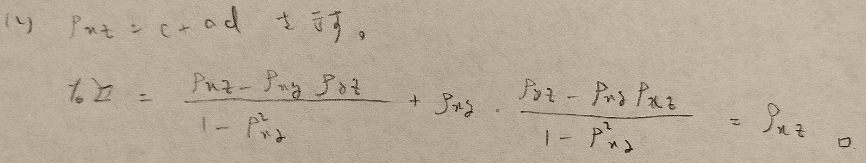
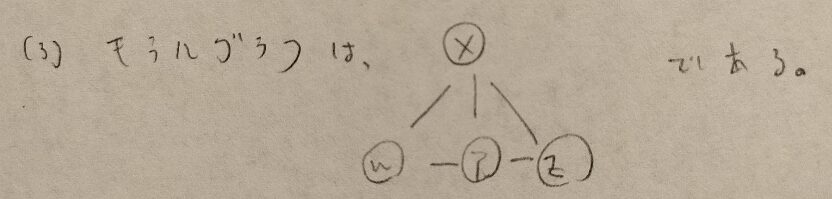
第25章メモ
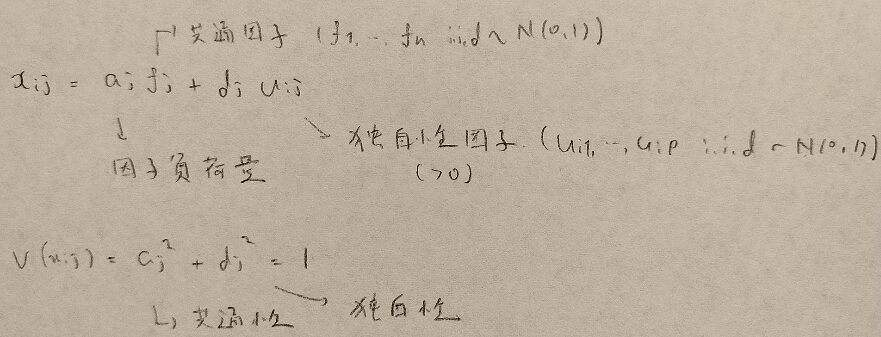
因子分析ではいくつかのポイントがあります。
因子負荷量の2乗が共通性になり、独立性因子の2乗が独立性になり、それらの和が1になるということですね。
その通りです。この関係は2因子モデル以上でも使えますので、ここがポイントになります。
問25.1の序盤ですね!
またモラルグラフを作る方法も大事です。
モラルグラフの作り方は次の3つのルールを覚えておけばOKです!
有効グラフAと無向グラフBについて
①AとBの頂点の構成は同じ。
②A上で2点で矢印で繋がっている点はB上でも無向辺で繋がっている。
③A上の点sが他の2点t,uから矢印で繋がっている場合、B上で点tとuは無向辺で繋がっている。
最後の③は経由を考えなさいということです。
統計検定準1級ワークブック解説:第26章『その他の多変量解析手法』
この章では主に3つの内容(多次元尺度法・正準相関分析・数量化法)を学習します。
これら3つも詳しい解説をした記事がありますのでご参照ください!
多次元尺度法
正準相関分析
数量化法→数量化Ⅰ類・数量化Ⅱ類・数量化Ⅲ類
数量化Ⅰ類→重回帰分析に相当
数量化Ⅱ類→判別分析に相当
数量化Ⅲ類→主成分分析に相当
数量化Ⅱ類は数量化Ⅰ類や数量化Ⅲ類(一般化が対応分析)よりもわかりやすいので判別分析の記事をご参照ください。
問26.1


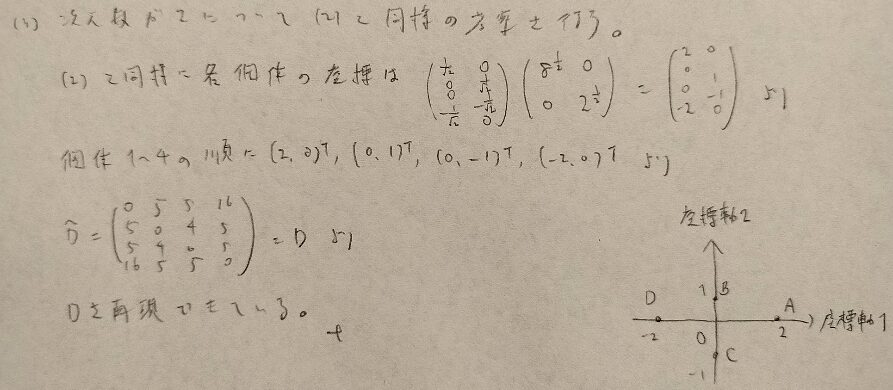
Dと一致する場合はエッカート・ヤング分解が成立していることになります。
第26章メモ
正準相関分析で2つの変数群のうち1つが1変数の場合が重回帰分析に対応しています。
重回帰分析の一般化が正準相関分析だったのですね!
その通りです。ちなみに変数群が1つの場合の正準相関分析のことこそ主成分分析だったわけです。
統計検定準1級ワークブック解説:第30章『モデル選択』
問30.1
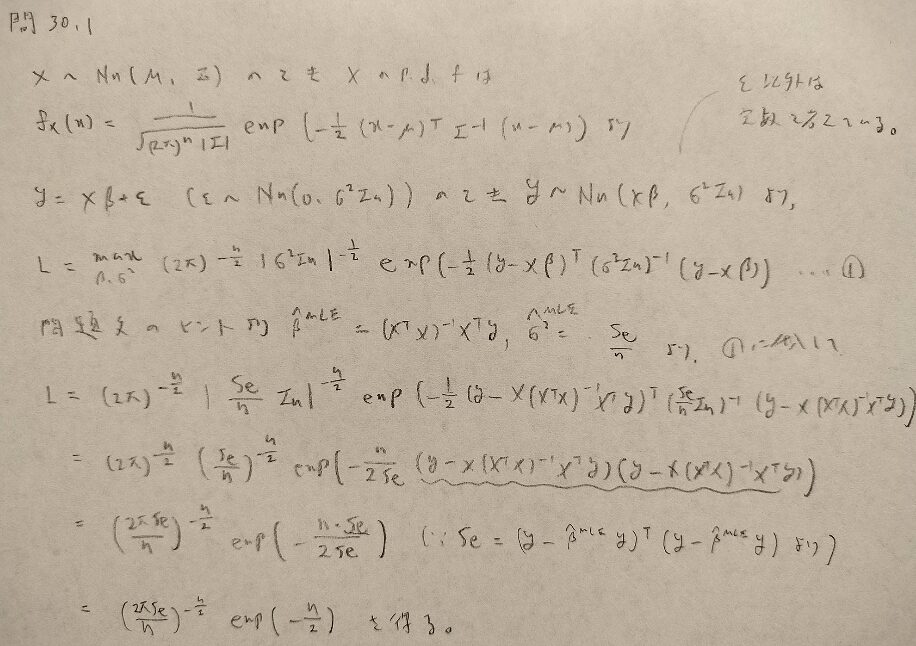
問30.2
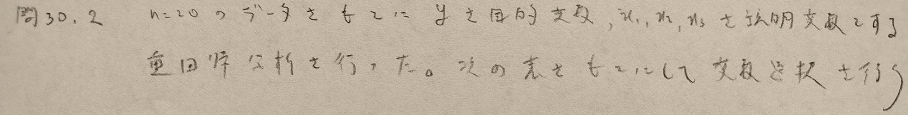
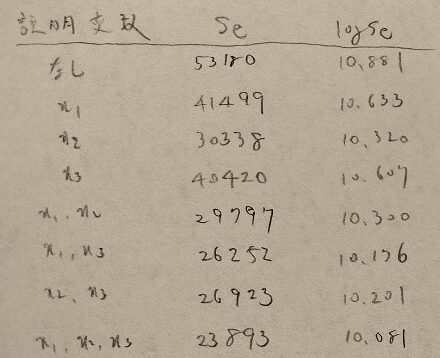
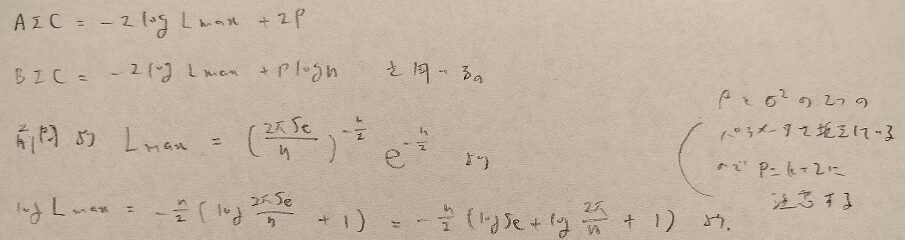
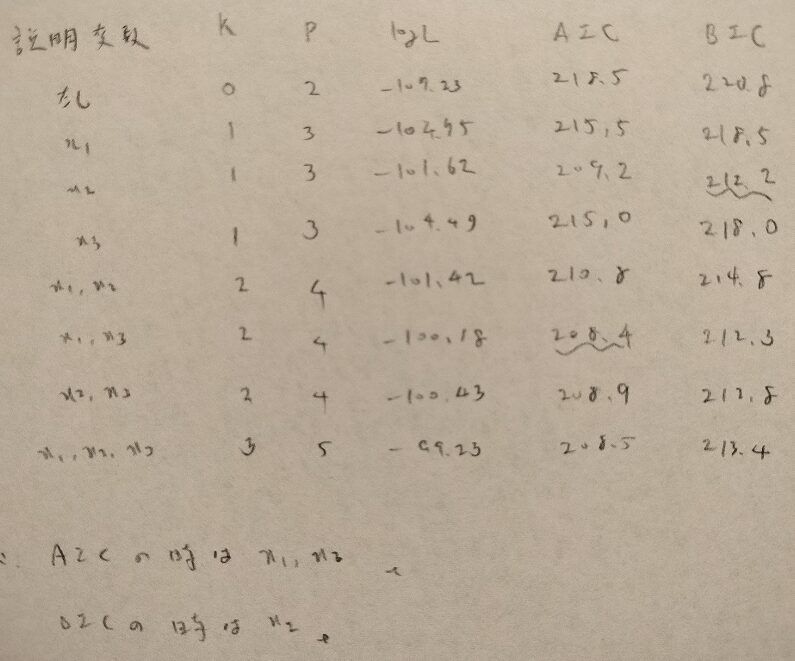
以上で統計検定準1級のワークブック『日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック』を用いた第Ⅲ部「多変量解析法」はおしまいです。
ワークブックの例題と問題はしっかり解けるように一緒に頑張って復習をしていきましょう!
しっかりと頑張れば必ず身につきます!
統計検定準1級の合格に必ず必要となるワークブックです。一緒に頑張りながら統計検定準1級合格をワークブックで勝ちとりましょう!


