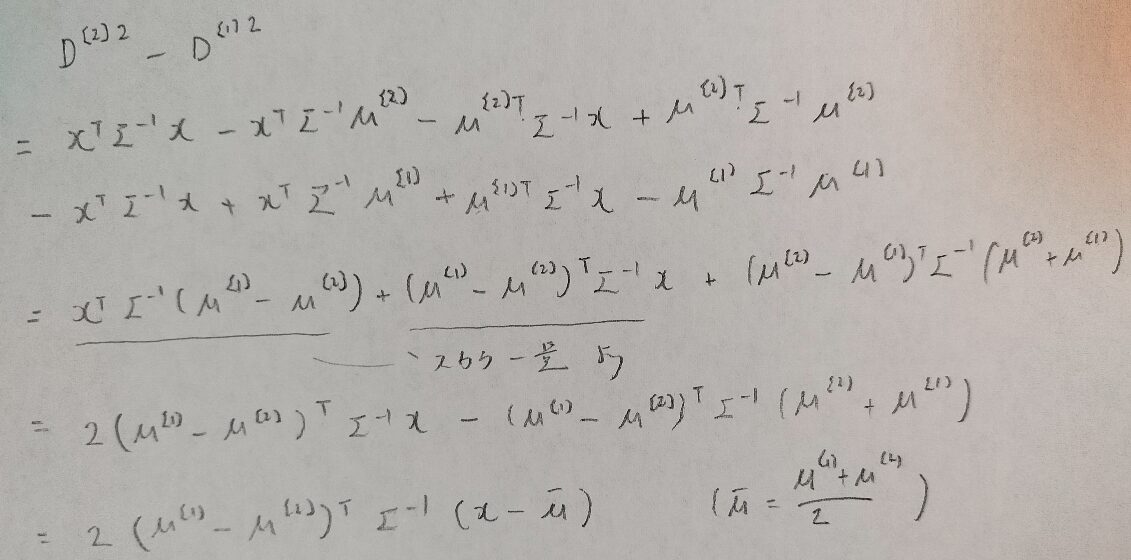母集団との距離の考えを用いて、サンプル(本来考えたい状況)がどちらの母集団に属するかを判別する解析法を判別分析といいます。
どちらの母集団になるのかをきちんと数学的に考えていくのですね。ただまったくどうやって判別していくのかが見えません。
たとえばあるXさんがいたとします。XさんはAグループとBグループのどちらに属しているかを考えます。通常の感覚だと、XさんとAグループの距離感と、XさんとBグループの距離感を考えて、距離が短い方のグループに属していると判断ができますよね。これと同じことを多変量解析で考えます。
判別分析は今まで学習してきた単回帰分析、重回帰分析、数量化1類と異なる点は、固有名詞が多く登場してくる点です。本記事ではその固有名詞にも注目していただけると良いです。また前回の記事以上に線型代数の2次形式関連の内容が頻繁に登場します。『これなら分かる最適化数学: 基礎原理から計算手法まで』が深い内容まで踏み込んでおりおすすめです。
たとえば今回登場する距離をマハラノビス距離といいます。実はこの距離は多変量正規分布から考えることのできる概念です。一緒に追っていきましょう。
判別分析(エクセルでも用いる)の行列表示
マハラノビス距離
判別分析を一般的な設定で考えていきます。p変量で2つの母集団を[1],[2]とします。また、判別分析ではxは多変量正規分布に従うと仮定します。
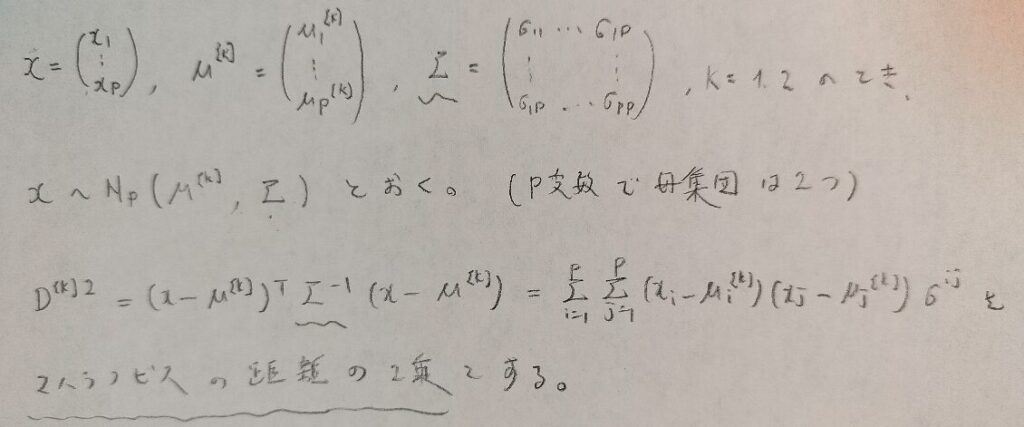
マハラノビス距離は2次形式で表現されるのでスカラー量になることに注目してください。本記事ではスカラー量になることに気がつかないと行列変形で行き詰まることがありますので、ご注意ください。
そしてマハラノビス距離は多変量正規分布の確率密度関数の一部になります。
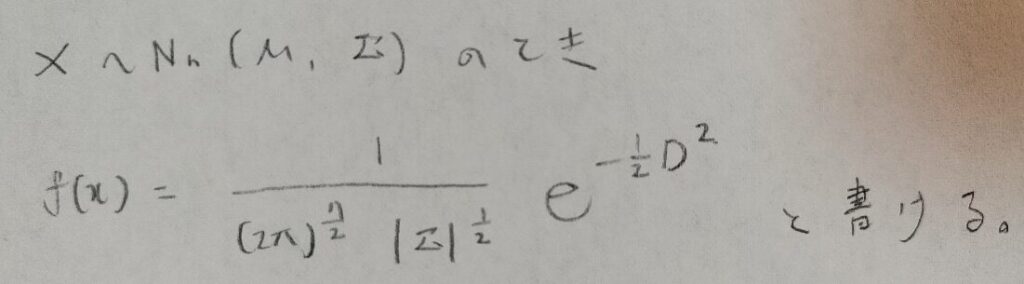
これはすごい!高校数学の数学Bでも出てくる正規分布の指数部分のごちゃごちゃしている部分の意味がマハラノビス距離だったのですね。感動です!
線形判別関数
次にマハラノビス距離を用いて、サンプルがどちらの母集団に属するかを判別するための関数を導きます。
先ほどのXさんの例で出てきた各母集団への距離の2乗を考えて、その差を計算で出せば良さそうですね。
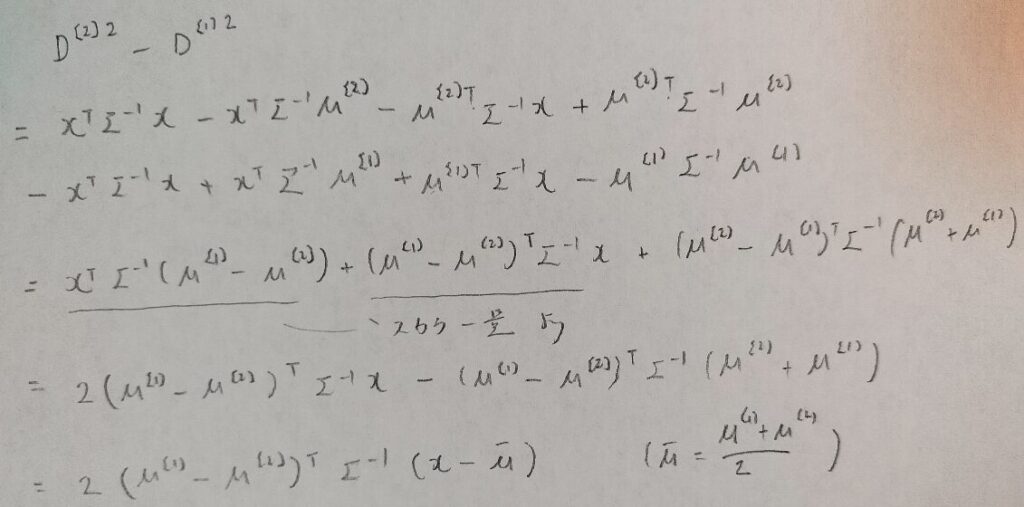
この係数2は定数なので、これを2で割った値を線形判別関数といいます。
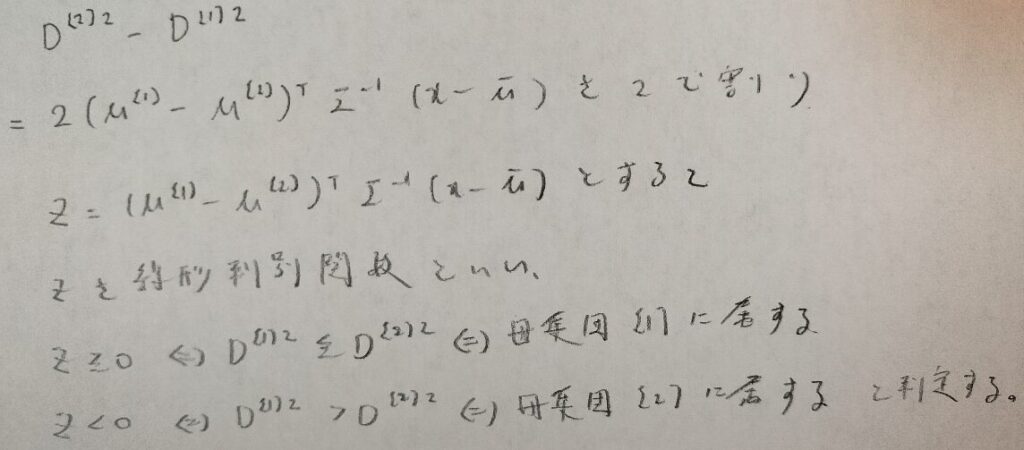
とてもシステマティックですね。
誤判断の確率
しかし時にはミス(本当に属する母集団とは違って誤判断される状況)が生じてしまうことがあります。これを誤判断といいます。
その確率はどれくらいですか?そもそも求められるのですか?
これもかなり面白いので、一緒に考えていきましょう。
誤判断の確率を求めるには、線形判別関数zが従う確率分布を求めれば良いです。
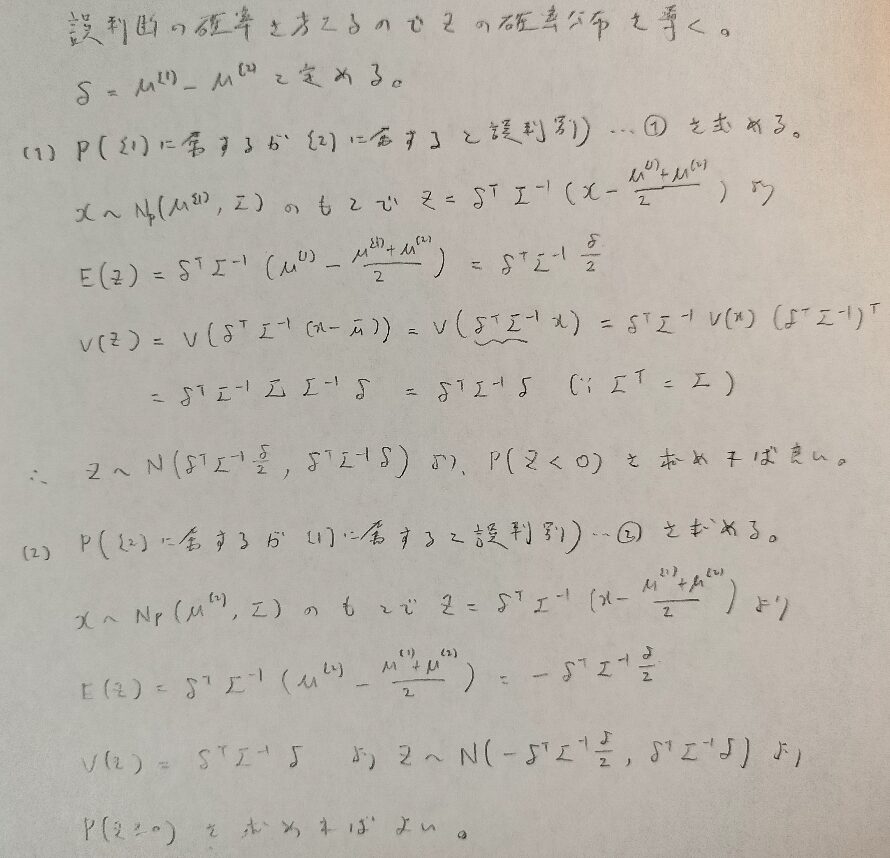
誤判断の確率を具体的に計算する方法を教えてください!
了解しました。実際に計算方法を導いていきます。
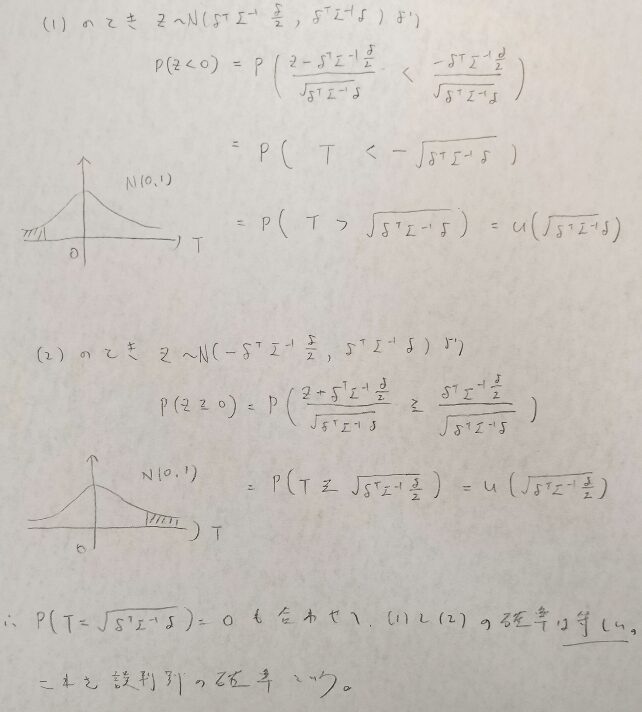
要するに正規分布表を見て計算できるのでとても便利なわけです。
でも、このδなどの値ってどうやって出すのですか?
そうなんですよね笑。そこが大事です。ここからは各推定値を出していくことになります。
要するに行列表現での限界が訪れたことになります笑
判別分析(pythonでも用いることがある)の期待値ベクトルや分散共分散行列の推定値
ここで登場する記号は数量化1類の記号の使い方とほぼ同じです。
母集団[1]の時の計算法を覚えれば、別の母集団の時も同じです。分散共分散行列行列が対称行列出ることにも注意しましょう。
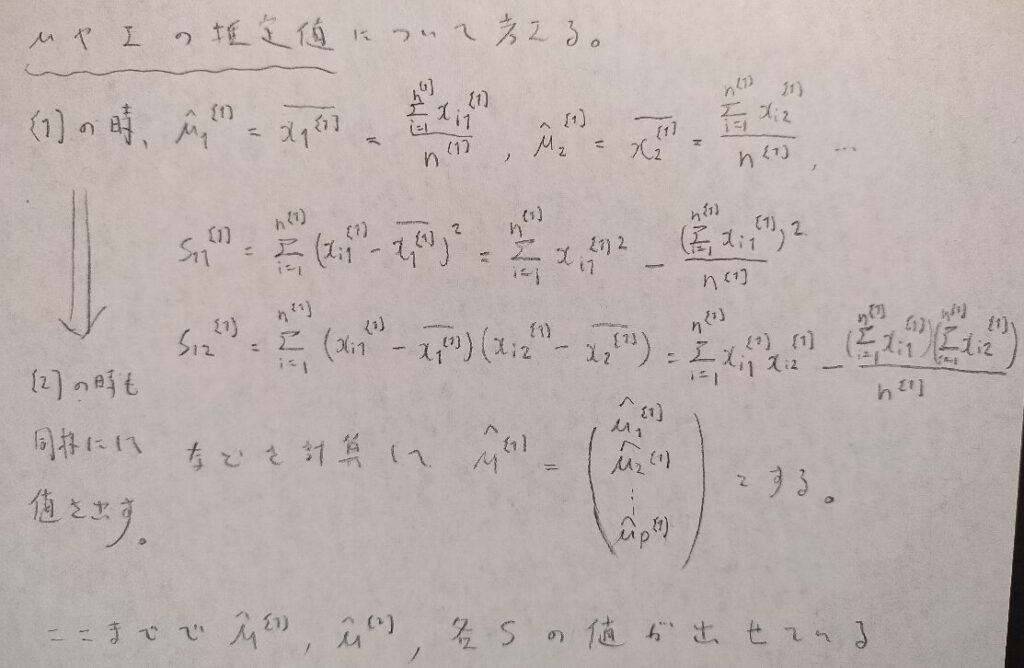
いよいよ分散共分散行列の推定値を出します。
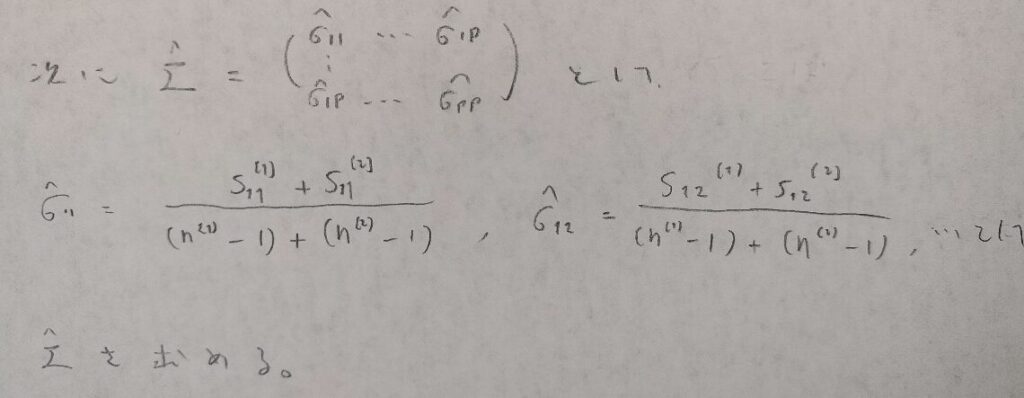
ここまでわかれば線形判別関数も自然に出すことができます。具体的な関数の式(一般に超平面の形)で出てくるので感動しますよね。
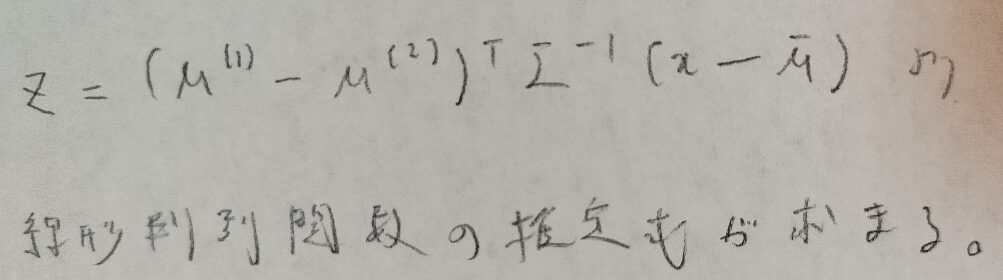
この関数の式にサンプルを入れて0以上か0未満化でどちらの母集団に属するのかが決まるのです。
ビシッと決まるのが良いですね。
判別分析(rでも用いる)判別表の使い方
判別表を用いれば、視覚的にわかる情報が増えます。

判別分析の変数選択(よりよい判別分析を行うために)
判別効率
判別効率という概念を学びます。どの変数を選択するか?によってマハラノビス距離が変わるからです。
2つの母集団間の距離が長い方が良い判別ができていると判断しそうですね。
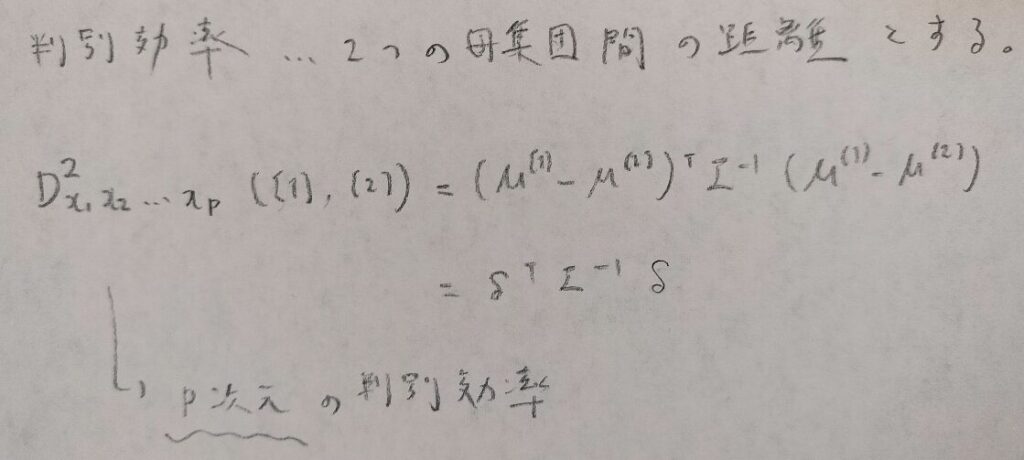
変数選択
判別効率の考えを用いて変数選択を行います。ここが最も難しいですが、統計検定1級などの試験では、そもそも判別分析などは計算量が多いため変数はそんなに多くはないです。そのため変数選択は理論面という認識でOKだと感じています。それに実際の過去問では重回帰分析に関する出題ですが、変数選択に関する数値は表で与えられており、言葉によって議論していくスタイルでした。

最後に具体的な式を提示します。『多変量解析法入門』によるとこれは母分散が等しい場合の2つの母集団の母平均の差の区間推定で用いる式から来ている式になります。
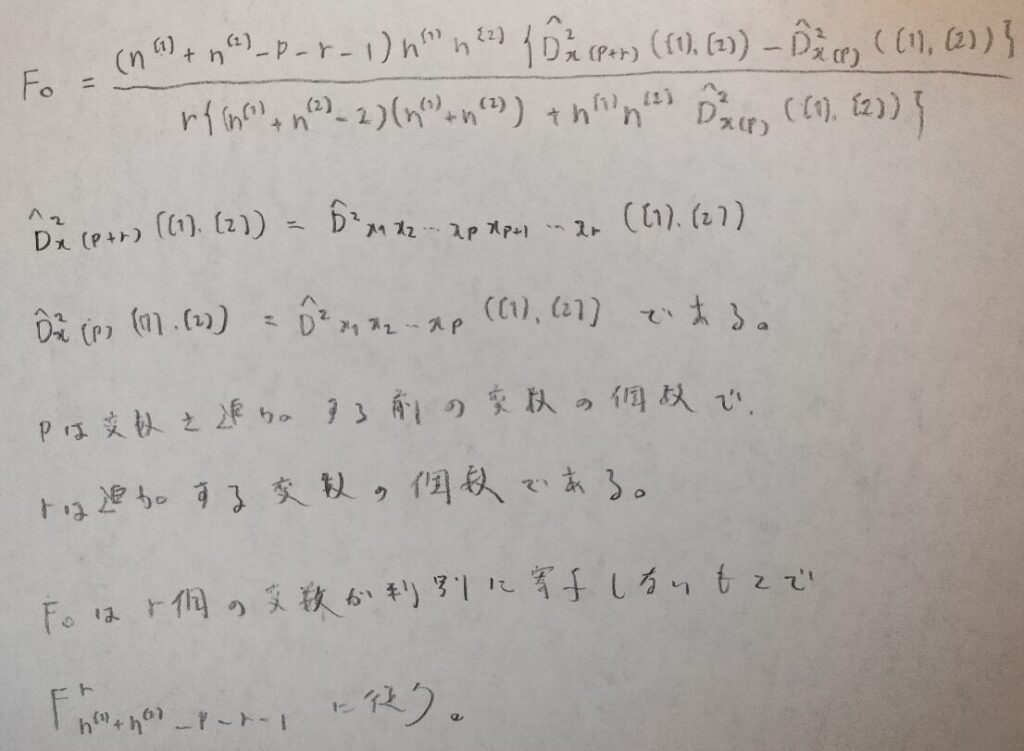
これらを用いて数量化1類でも出てきた変数増減法などを用いて適切な変数を選択した上で、判別分析を行うのですね。
その通りです。お分かりのとおり、手計算ではかなり時間がかかり厳しいので、エクセルやpythonやrやspssなどで解析を行なっていきます。
これらのことから、統計検定1級では計算結果が与えられて、それらをどのように用いていくかの理解度が今後問われる出題になると予想できますね!
今回もありがとうございました。永田先生の『多変量解析法入門』は名著ですのでご紹介させていただきます。統計検定1級合格者からは「必要な知識がギュッと詰まっている」との評判が多々ある素晴らしい学習書となっております。