指数分布の次の分布はどの分布ですか?
指数分布が組み合わさってできる分布はいくつかあるのですが、今回は2つの指数分布の差で作られるラプラス分布について解説します。
この話題は統計検定1級やアクチュアリー数学といった難関資格での頻度は低い傾向にありますので、掲載されている参考書は少ないです。加えてデルタ分布が掲載されていた『リスクを知るための確率・統計入門』でさえも少しの説明のみとなっております。
なぜマイナーな分布を扱うのですか?
ラプラス分布を考えることによって、確率変数の変数変換と標準化について考えざるを得なくなるからです。
ラプラス分布の一般化ならびに期待値と分散を求める際に、分布の対称性に関する考え方なども盛り込んで解説していきます。
確率変数の変数変換(1変数)
今回のテーマであるラプラス分布は2つの確率変数間の関係で構成されます。そのため確率変数同士の変換について事前に知識を入れておく必要があります。
今回は2変数の場合との論理の流れを考えて、1変数の場合において分布関数から導くのではなく全確率1から導く方針を取ります。
1変数の場合は一般化した考えではなく、具体例で考えた方が分かりやすいので、次の例を参考にしましょう。
どんな例ですか?
確率変数Xの分布が与えられているときに、Y=aX+bで作られる新たな確率変数Yの分布(確率密度関数)が求めたい例です。
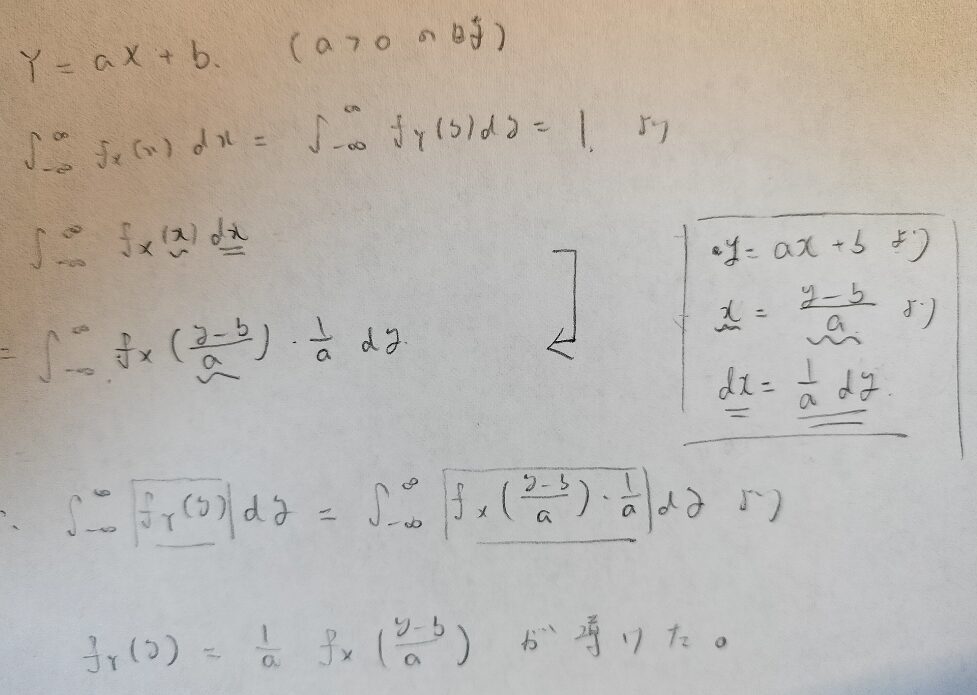
全確率1が出発点となる考えですね。
この考え方は『確率統計キャンパス・ゼミ』で紹介されていて、僕が初めて知った確率変数の変換の証明法でした。とても分かりやすいと感じたので紹介しました。
確率変数の変数変換(2変数)からの差の公式の導出
いよいよ確率変数の変換ではメインのお話です。この方法が身につけば様々な変換の問題に対処できます。
全確率1から出発する点は1変数の時と変わりません。今回はヤコビアンが登場するので、不安な方は『微分積分キャンパス・ゼミ』をご覧ください。
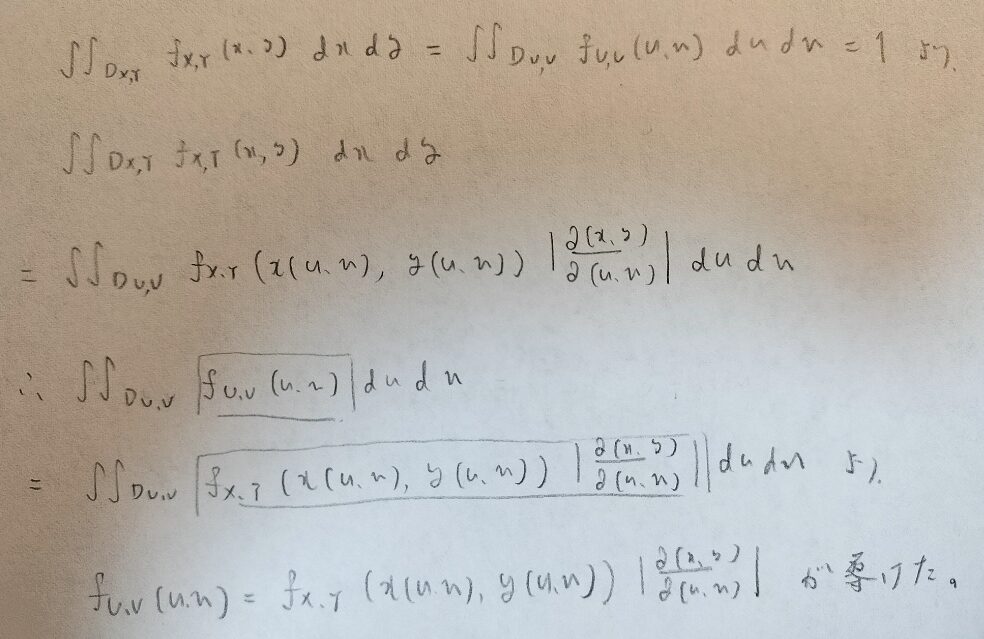
これでは抽象的だと思うので、ラプラス分布を導く際に用いる確率変数の差の公式を導いてみます。X,Yが与えられている確率変数で、Uが従う分布を考えていきます。
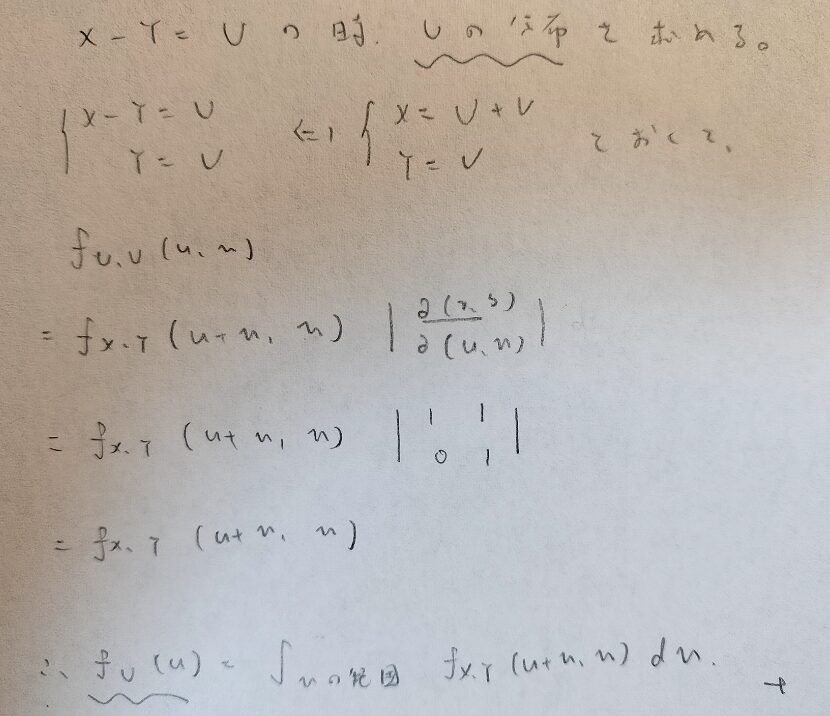
まだまだ抽象的ですね。
これから具体例を出していきます。
標準ラプラス分布は指数分布の差から作られる
まずはラプラス分布とはどのように作られるのかをざっくりと説明します。
ラプラス分布は指数分布の差から作られる分布です。
きちんとした定義に行くために、『現代数理統計学の基礎』を参考にした次の記号を定義します。
XとYが独立で同一分布Fに従うとき、X,Y, i.i.d. ~ Fと表記します。XやYは複数個あっても構いません。
ラプラス分布について上の表記を用いた定義を教えてください。
X,Y, i.i.d.~Ex(1)のときに、Z=X-Yで定義されるZの分布を標準ラプラス分布といいます。
さきほど導いた差の公式を用いて標準ラプラス分布の確率密度関数を導いてみます。方針としては、あとの話題のためにパラメータを1ではなく一般的なλとして導いた後でλ=1とします。
次の解説の4、5行目は被積分関数を指しています。=で結ばれていたりするため表記ミスです。すみません。
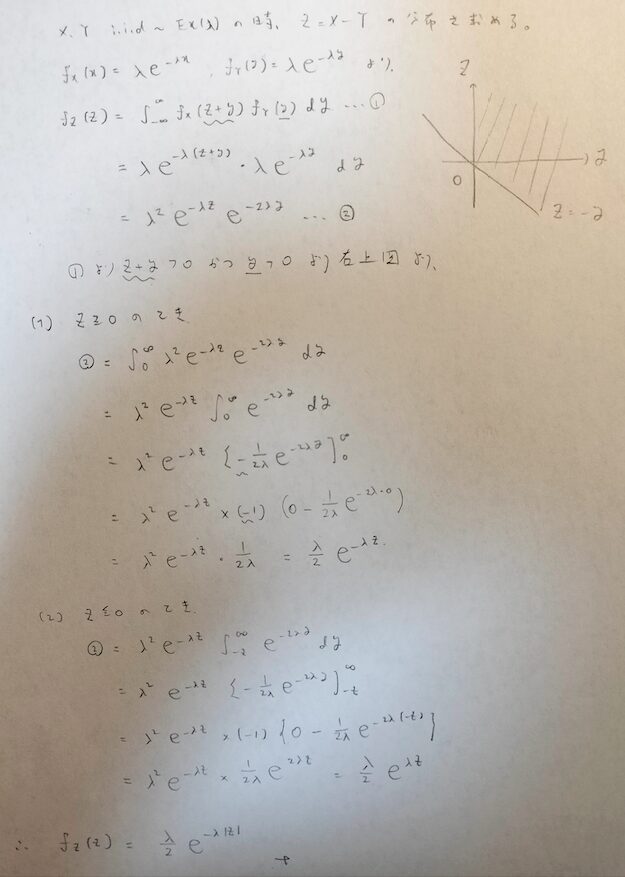
この結果は最後の章でラプラス分布の注意点のときに再度使います。
最後にλを1にすると次のような式が導かれます。これが標準ラプラス分布の確率密度関数です。
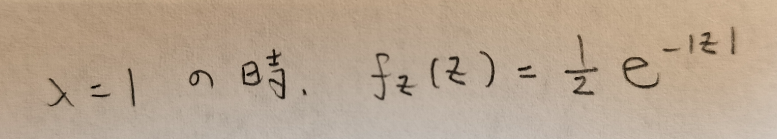
標準ラプラス分布ということは一般のラプラス分布もあるのですね?
良い質問ですね!一般のラプラス分布もあります。ただしこちらを導くための事前準備が必要です。
確率変数の標準化からラプラス分布の確率密度関数を導く
中心極限定理などでは確率変数を標準化することが要求されます。そのために今回のラプラス分布で標準化の考えを紹介します。
標準化とは何をするために行うのですか?
受験数学では二次関数を標準化して頂点などを求めますよね?確率変数も同様で、標準化をすることによって様々な問題に対応することができます。例えば次の定理があります。どのような確率変数も期待値と分散が定まっていれば、標準化されたZの期待値と分散は必ず0,1になるのです。
不思議なので証明を知りたいです。
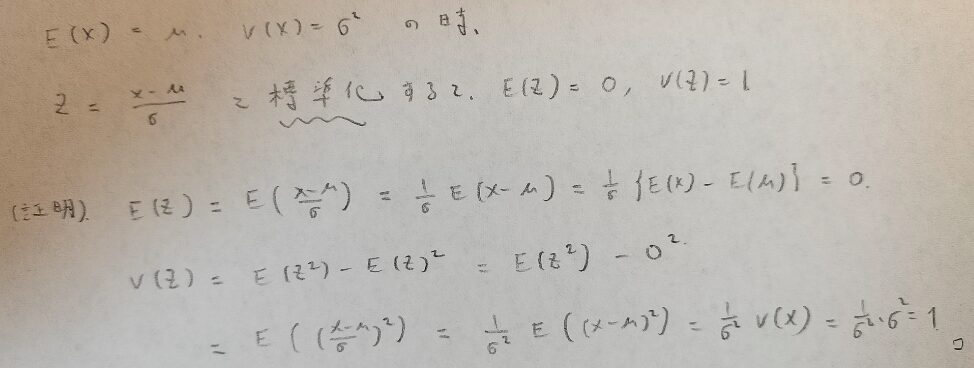
受験数学の二次関数では標準化の反対は一般化でした。では標準ラプラス分布を一般化するにはどうすれば良いでしょうか。
標準化と逆のことをすれば良いのですね!
それでは一般のラプラス分布の確率密度関数を導きます。
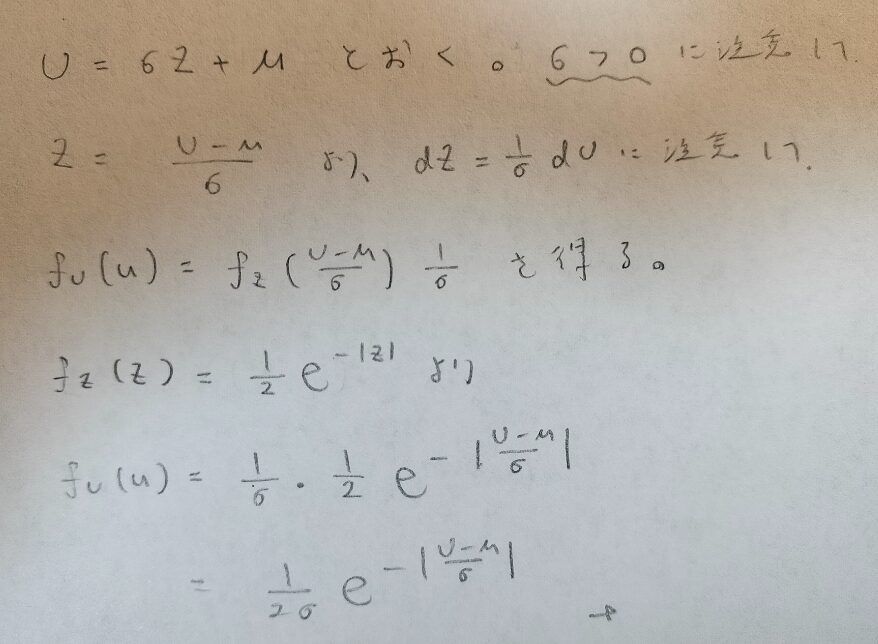
ずっと気になっていたのですけど…
はい。何でしょう?
ラプラス分布の記号ってあるんですか?
一生懸命探したら、見つかりました!笑
上の確率密度関数に従うUのことをU~DEx(μ,σ)と表記します。σとはシグマの小文字です。こちらの表記は『現代数理統計学の基礎』の巻末から抜粋しました。ラプラス分布は両側指数分布とも呼ばれて、英語名がdouble exponential distributionです。その頭文字をとってDExと呼ばれています。両側指数分布なので対称なグラフになります。
確率変数ということは全確率1ですよね?
もちろんです。証明しましょう。さりげなく置換積分の際に標準化の考えを使っています。
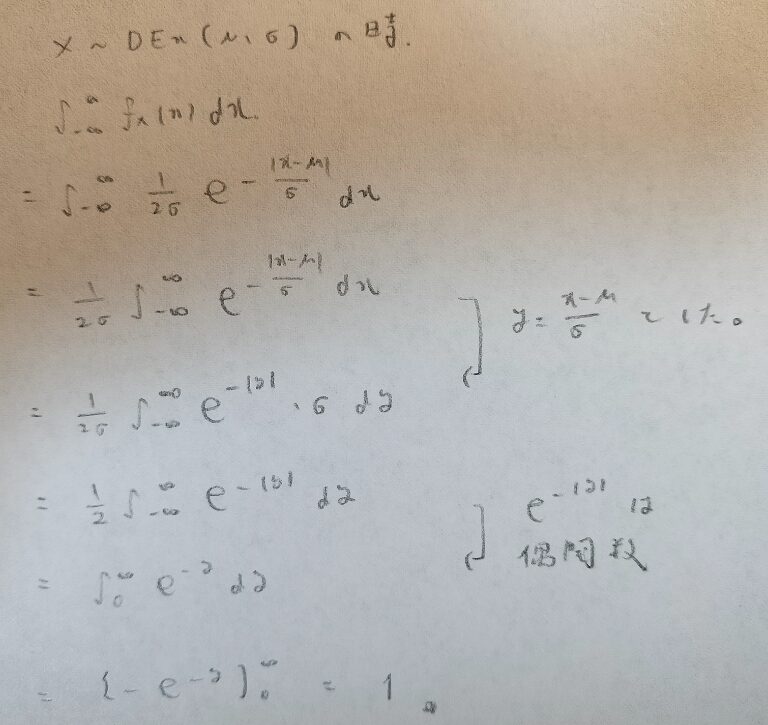
ここで偶関数の知識を使いました。あとで奇関数の知識が必要な場面があります。
ラプラス分布の期待値をグラフの対称性から求める
ラプラス分布の期待値を真正面から出そうとすると計算が複雑になります。そのため『現代数理統計学の基礎』ではとある定理が紹介されていますので紹介します。
確率変数Xが従う確率密度関数をf(x-μ)とするとき、全ての実数yに対してf(y)=f(-y)であるならばE(X)=μである。
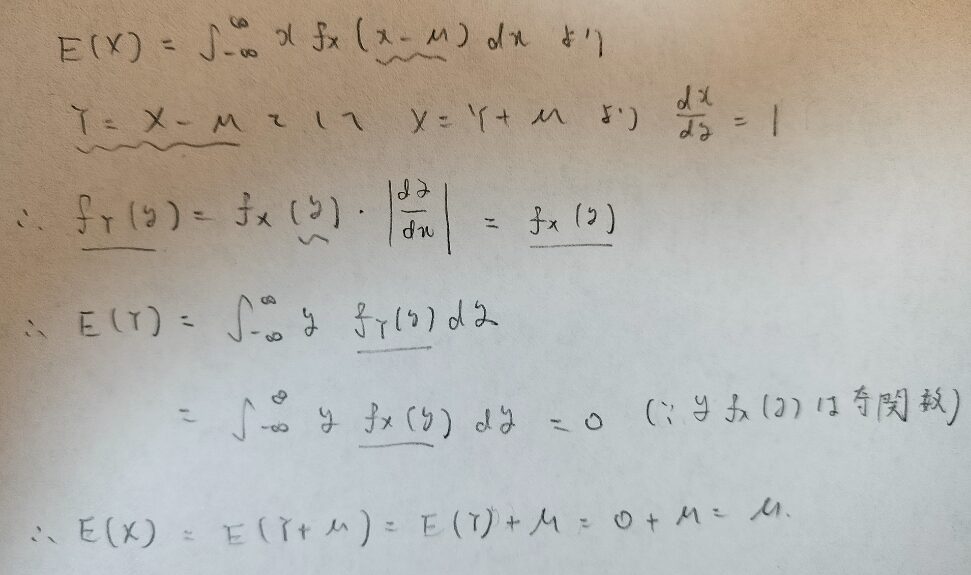
確率変数の変換を用いてますね!
ラプラス分布ではこの話題が本質かも知れませんね。上の定理を用いてラプラス分布の期待値を求めますが一瞬で終わります。
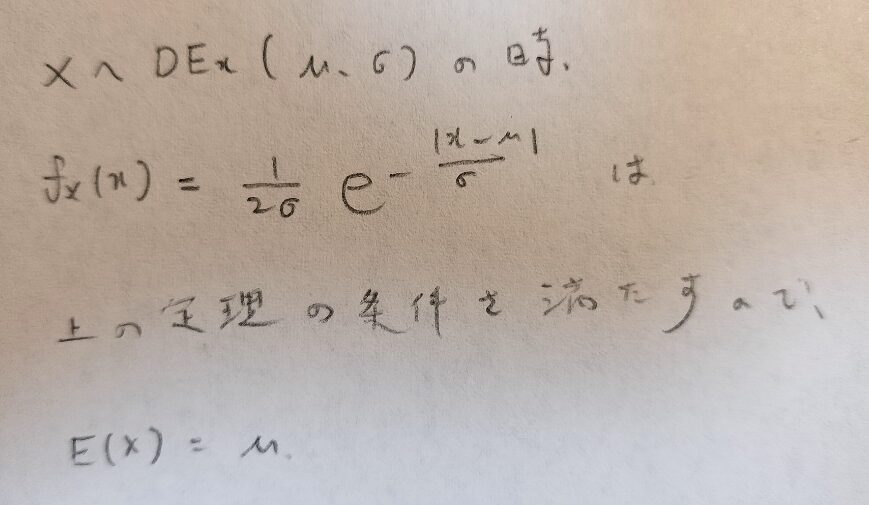
ラプラス分布の分散は分散の定義の通りに計算する
分散の計算ということは、離散分布ならX(X-1)の期待値を出し、連続確率分布ならXの2乗の期待値を出しておくのが定石でしたね。
ラプラス分布では思い切って分散の定義に従う方が楽なのです。その理由は置換積分の箇所を見れば分かります。
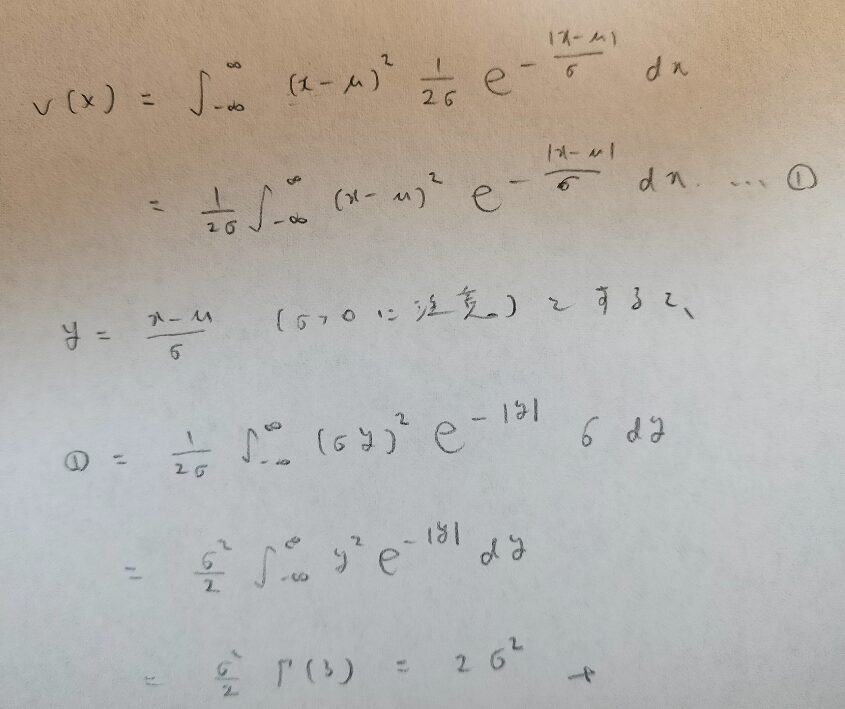
そうか!標準形の知識があれば、分散の定義式そのものが標準形の形を使うヒントになっているからですね!
その通りです。
標準ラプラス分布の期待値と分散とラプラス分布を扱う際の注意点
標準ラプラス分布を出した際の一般形の確率密度関数を再度持ち出します。
標準ラプラス分布の期待値と分散っていくつなのか考えていたら混乱しました。
これは僕も混乱した時がありました。アクチュアリー数学の過去問で「答えが合わない!」ってなったんです。ポイントはパラメータをどのように見るか?という着眼点を持つことでした。この話題はガンマ分布のときも1番の注意点として登場するので考え方を覚えておいてください。
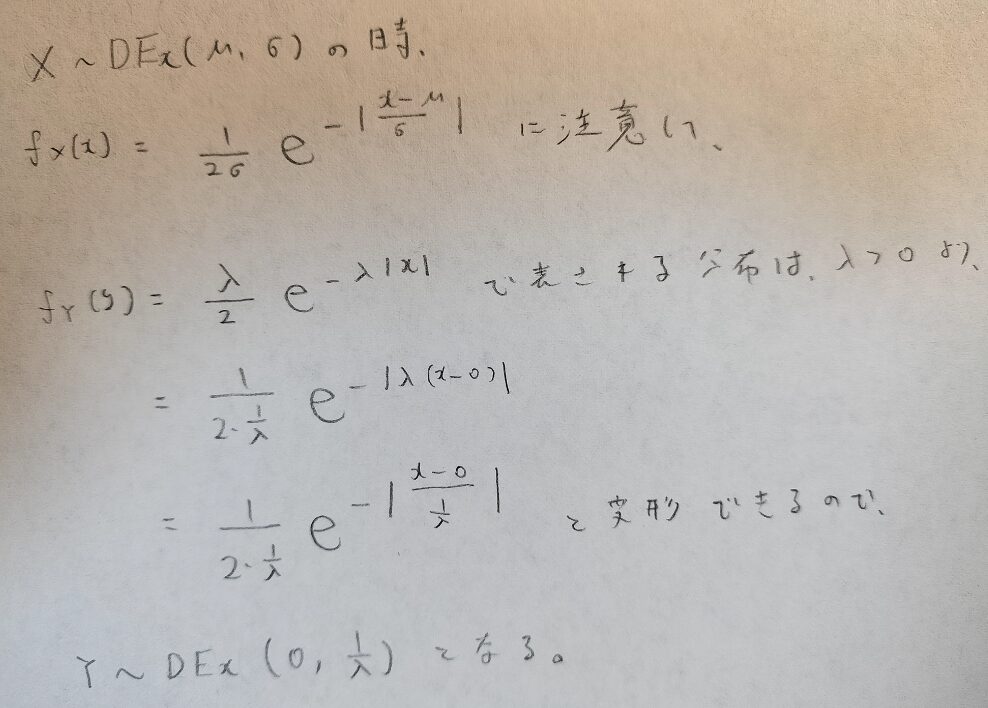
分かりました!標準ラプラス分布はλ=1とすれば良いので、Y~DEx(0,1)ですね!
ここで標準ラプラス分布において期待値0で分散1とするのは間違いです。
違うんですか?!
期待値は合っているけど、分散が間違いです。
X~DEx(μ,σ)のときに期待値はμですが、分散はσの2乗をしたものを2倍した値です。
なるほど!分かりました!標準ラプラス分布の分散は1の2乗をしたものを2倍したものなので答えは2です。
最後にラプラス分布の記事を書く際に参考にした本を紹介します。
重積分のヤコビアンの理解がとてもしやすくおすすめです!
確率変数の変換の説明で全確率1からスタートしている流れがとても分かりやすいです。僕も困ったときは全確率1からスタートしています。
ラプラス分布のグラフが紹介されています。パラメータを変えたときの様子が書かれていて分かりやすいです。
ラプラス分布についてもっとも詳しい説明が書かれている本です。本記事で紹介した定理も本書の練習問題からの抜粋です。






