統計検定1級の新たなバイブルとして青本という名前で親しまれている久保川先生の『データ解析のための数理統計入門』を第1章から自力で解いていき、皆様と共に注意すべき箇所などをまとめた記事になります。
そして本章である第3章は統計検定1級に頻出の変数変換が登場してきます。またアクチュアリー数学でも頻出な条件付き分布の有名公式の導出問題など、例題や演習問題のボリュームが増えてきます。
∩∪⊂∈←よく使う集合記号です。コピペなどにご活用ください。
本章では重積分がたくさん出てきます。実際に統計検定1級でも基本的な計算はできないと時間内に間に合わないため、本番と難易度がほぼ近い本書の例題や演習問題を自力で解けるようになることは、現在の統計検定1級の難易度を事前に把握しておく意味で大切です。
統計学の青本の第3章のための前提知識
本章は様々な事前知識が要求されるため、この節にてまとめておきます。
3次元以上の確率分布における同時分布は次のように定義されます。他の例も同様です。Σ記号の下の部分の記号は、確率変数がとりうる実現値の集合を意味しています。
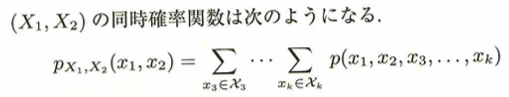
連続型の確率密度関数でもその値は必ず0以上です。
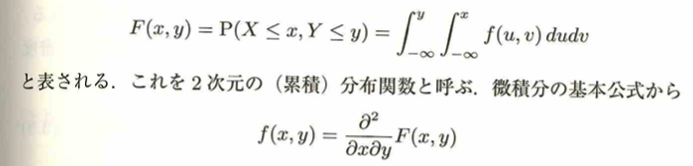
多変量正規分布は一般形で覚えておいた方が応用が効きそうです。

なぜこの式が出てくるのか?の理屈はこちらで解説しています。
多変数の時、独立性の定義は同時分布関数(すべての実現値において)が周辺分布関数の積で書けるときを指します。この定義からよく知られている、同時分布が確率密度関数の積で表されれば良いという定理が導かれます。
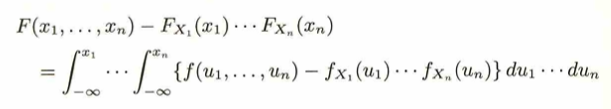
上の式は確率密度⇒分布関数の証明で、逆はn個の変数における偏微分を順次行うことにより示せます。
この独立性の定義の部分って盲点なんですよね。
事象の独立について事象 Aと 事象B が独立であるとは一方の事象が起こるかどうかが他方の事象の確率に影響を与えないことを指します。確率変数の独立において確率変数 Xと 確率変数Yが独立であるとは片方の変数がどの値を取るかが他方の確率分布に影響を与えないことを指します。
条件付き分布において、条件付き確率密度関数の全確率は1になることにも注意しましょう。以下は応用で大事な2変量正規分布に関する重要な公式です。
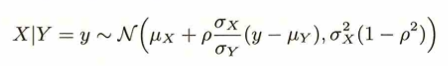
この公式の期待値の部分の相関係数記号を標準偏差表記で書き直すと、のちに紹介させていただく一般形との関連性が見えてきます。実は先ほどの多変量正規分布の記事でもこの導出を高次元の観点から導出したのですが、とても応用が効きそうな方法なので本記事にも掲載いたします。


この公式は『増訂版 日本統計学会公式認定 統計検定1級対応 統計学』から抜粋させていただいております。公式本以外でこのブロック化の考えを用いている書籍を僕は知りません。
本記事のメイン本『データ解析のための数理統計入門』では、2変量正規分布の形に注目して、平方完成をして直接解答を導いています。
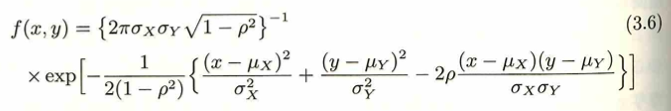

この結果より2変量正規分布の同時確率密度関数の式は上の2式の積で表現できます。第1式が所望の条件付き分布の式のため、期待値と分散を読み取ります。
この直球勝負の式変形はアクチュアリー数学で出題されております。本質部分はu,vを見抜けるか?という点です。
この方法は慣れれば直感的な方法ですね。先ほどのブロック化の方法の方が抽象度が高めですね。
久保川先生の青本の第3章の例題
例題や演習問題を通してベータ分布に帰着させるタイプの問題がラスボスになっています。このタイプは一度解いていないと初見で解法を思いつくのは難しいと思いますので、一緒に頑張って消化していきましょう。詳しい問題文は本書『データ解析のための数理統計入門』に掲載されています!
同時分布の作り方
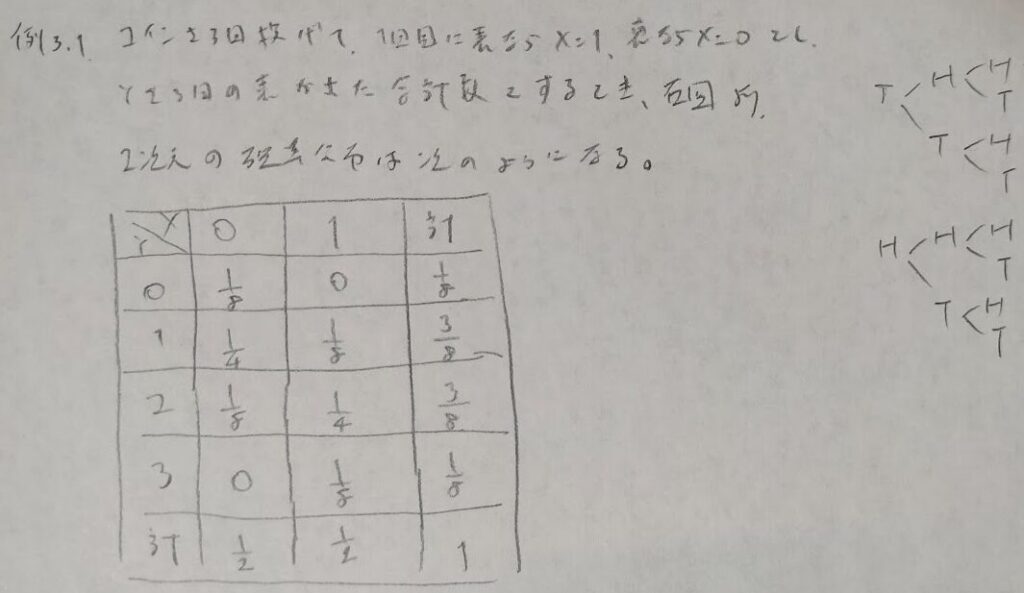
同時分布とは表のことです。
分布関数の使い方の盲点

類書では見ないタイプの問題ですが、分布関数の定義を理解できているか?を問う良問です。
正規分布の再生性の証明
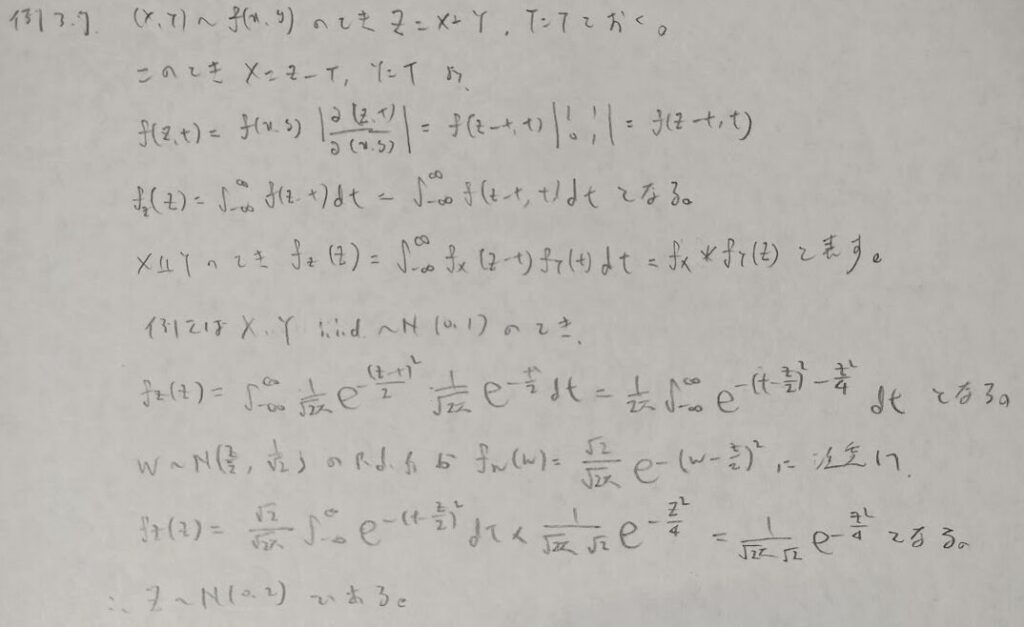
本問の難しさは最後の正規分布に帰着させるところです。特に分散の値を見抜けるか?が勝負です。再生性の結果を知っている人は答えから逆算しても良いと思いますが、実際はその逆の流れで答案が書けると素晴らしいですね。
ガウス積分
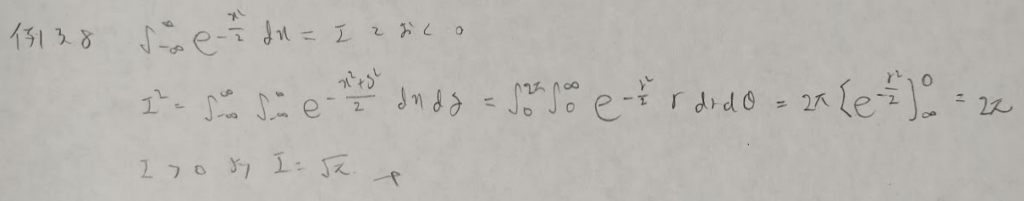
第3章で最も簡単な問題です。ガウス積分が最もわかりやすく解説されている参考書は『微分積分キャンパス・ゼミ』です。
ベータ分布に帰着させる頻出問題
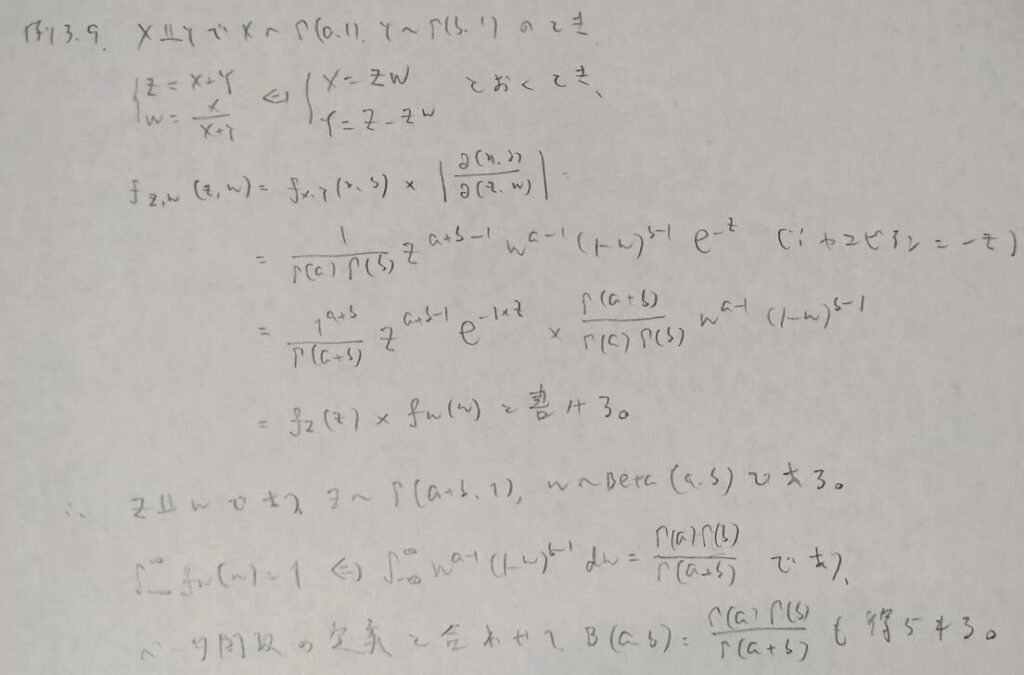
後の演習問題ではディリクレ分布というベータ分布の上位互換の問題として再登場するタイプの問題です。とにかく「ベータ分布に帰着させる!」という強い気持ちを持って取り組みましょう!
青本第3章の問題(条件付き分布など)
四面体問題
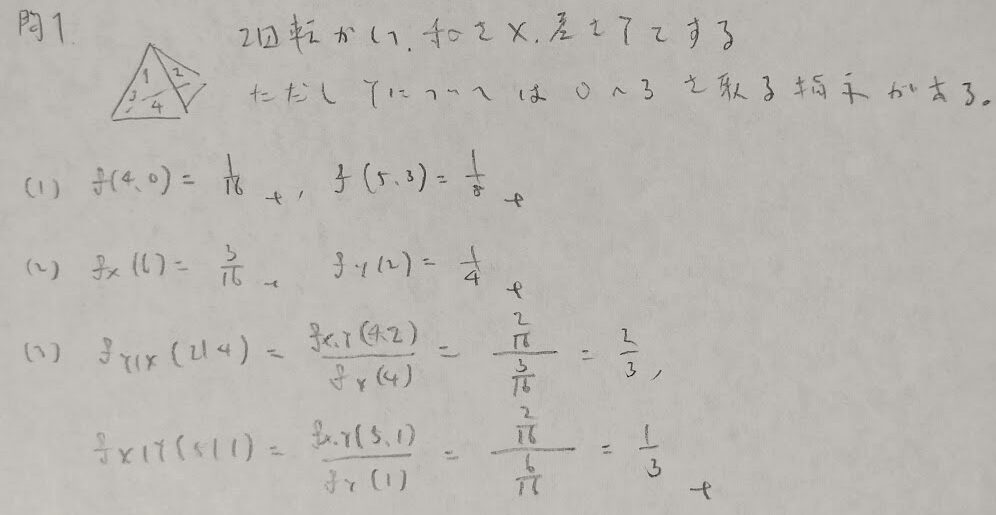
差の意味が難しいですが、問題文にその値がとり得る範囲が書いているので、引く順番に問題はないとわかります。
多項分布の有名公式

この結果はアクチュアリー数学で頻出です。マーク式の試験の場合は公式がスッと出てくるように下記のtweetをご参照ください。
ポアソン分布と二項分布の関係
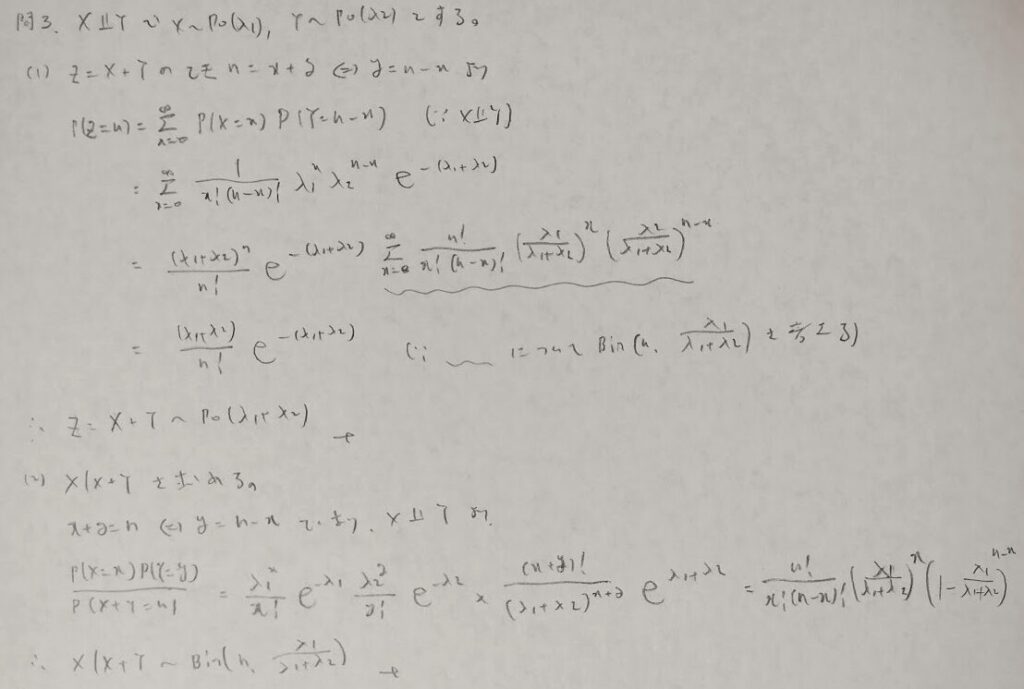
この問題も先ほどの問題の類題です。アクチュアリー数学には未出(2025年夏現在)です。波線部分に気づけるか?がポイントです。
ガンマ分布への帰着
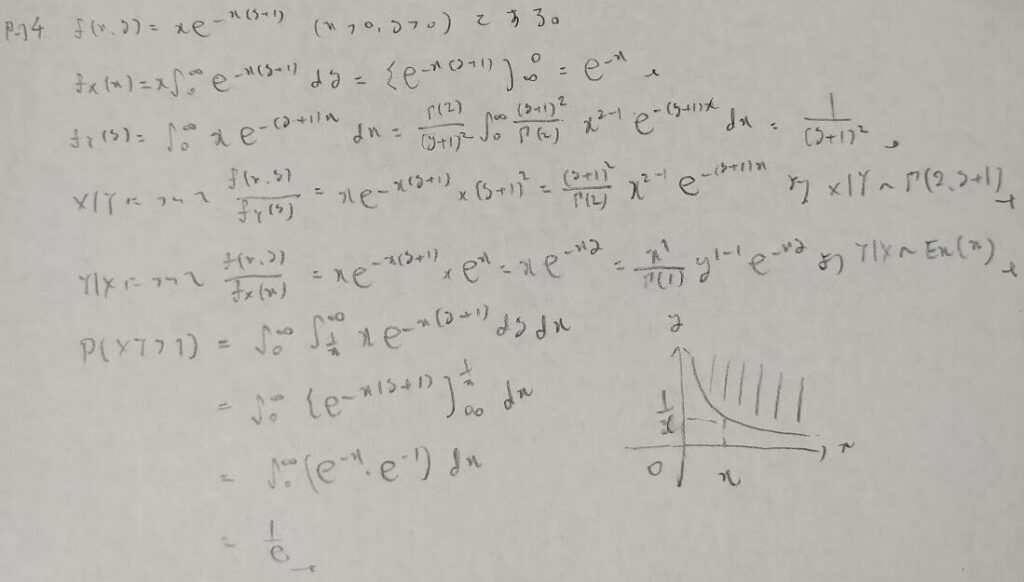
ガンマ分布に帰着させるタイプはかなり有名です。最もわかりやすい説明は藤田先生の『弱点克服 大学生の確率・統計』です。この本はアクチュアリー数学の内容をギュッと1冊に濃縮した素晴らしい本です。
積分範囲の図示

最後の問題は重積分の問題です。積分領域さえ見抜いてしまえば後は計算でのゴリ押し勝負です。
一様分布と指数分布の関係
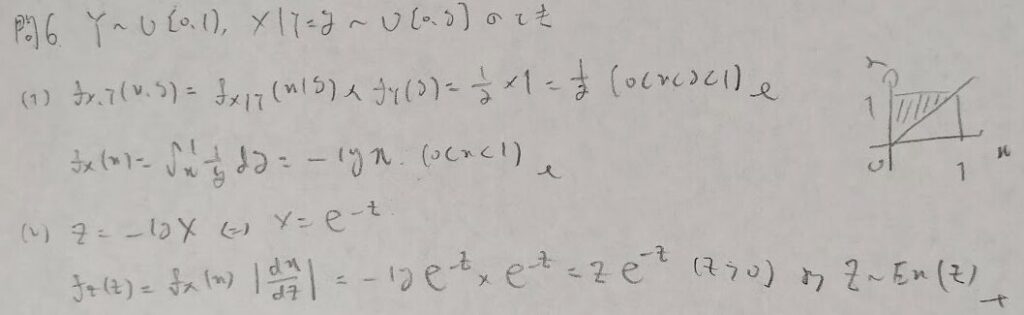
統計検定1級でもアクチュアリー数学でも狙われるタイプの問題です。一様分布と指数分布は変数変換で結ばれています。
ディリクレ分布の有名公式
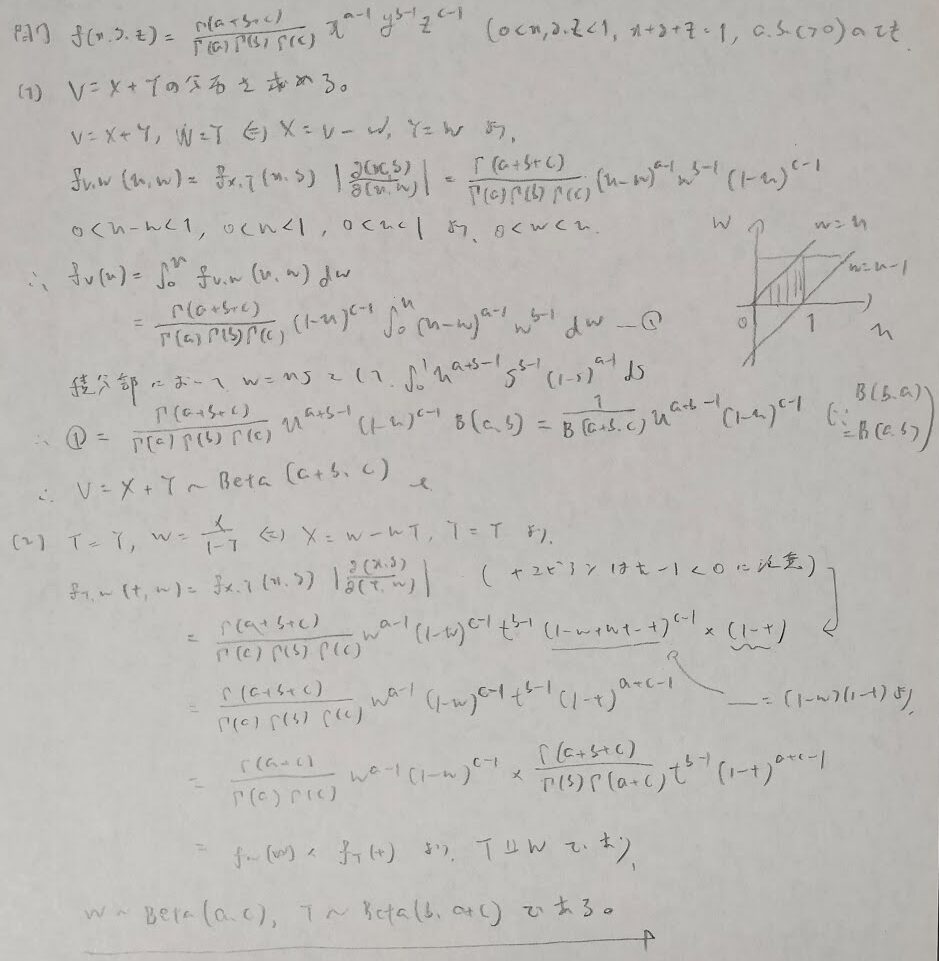
本問は第3章で群を抜いて難しいです。難所のポイントは2つあり、まずは(1)の積分範囲の図示です。久保川先生の模範解答では省略されていたため、大学受験数学のような考えを用いて解いてみました。そして(2)の最後のベータ分布への帰着に気付けるか?がまた難しいです。
統計検定1級では未出(2025年夏現在)のタイプのため、しっかりと解けるようにしておきたいですね!