統計検定1級の対策書として真っ先に買うべき本である『データ解析のための数理統計入門』の第4章の解説と演習問題を自力で解いた学習の軌跡の記事です。本章の問題からグッとボリュームが増えて、難易度が高い問題が増えます。しかし統計検定1級のレベルを逸脱するような奇問は非掲載のため安心した学習が可能です。
統計検定1級の新たなバイブルとして青本という名前で親しまれている久保川先生の『データ解析のための数理統計入門』を第1章から自力で解いていき、皆様と共に注意すべき箇所などをまとめた記事になります。
本章は類書で薄くなりがちな多変量正規分布をはじめとした多変量分布、そして統計検定1級やアクチュアリー数学で合否を分ける条件付き分布に関する問題を徹底して訓練できます。本章だけでも『データ解析のための数理統計入門』を購入する価値があります。
∩∪⊂∈←よく使う集合記号です。コピペなどにご活用ください。
第3章よりボリュームが増えています。難しく感じる方は過去記事も合わせて学習ください。
条件付き分布などの事前知識と多様な例題
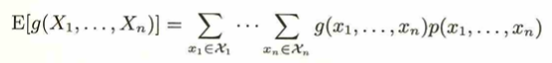
同時確率関数p(x_1,…、p_n)における期待値の定義です。連続版はΣが積分記号に変わるだけで大きな変化はありません。
あまり頻繁に登場しないこともあり、盲点的な定義になりますね。
期待値が存在するとき、E(|g(x,y)|)<∞などとします。
期待値記号の中の文字がXならばf(x)を考え、X,Yの場合はf(x,y)を考えることになります。これらの考えは期待値の性質証明において重要な方針を与えます。
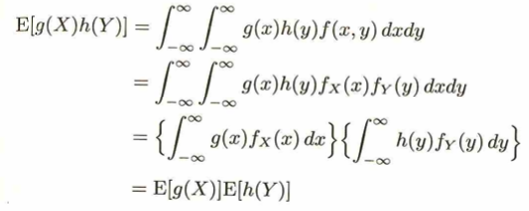
標準正規分布から歪度と尖度を定義できます。
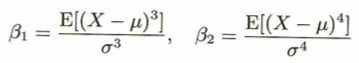
『データ解析のための数理統計入門』の尖度の定義では、正規分布のときは3になります。
マルコフの不等式からチェビシェフの不等式の導出も自動化しておかないと統計検定1級の統計数理の合格は難しい印象です。

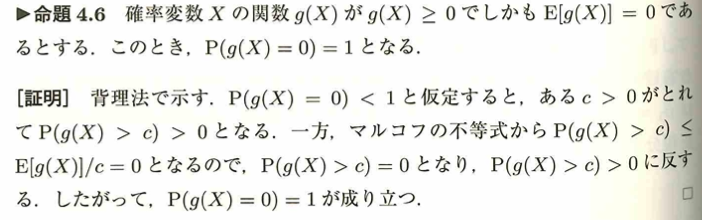
マルコフの不等式は存在命題であり、背理法と相性が良いことを物語っています。
『データ解析のための数理統計入門』にはこのような応用上で汎用性の高そうですが、類書には掲載されていない命題が多く載っていることも良いポイントです。
共分散は平行移動について不変ですが、尺度の取り方に依存します。その欠点を解消したものが相関係数で符号を除き尺度の取り方に依存しません。
相関係数の絶対値は1以下であることからコーシー・シュワルツの不等式が導けます。また独立⇒無相関です。
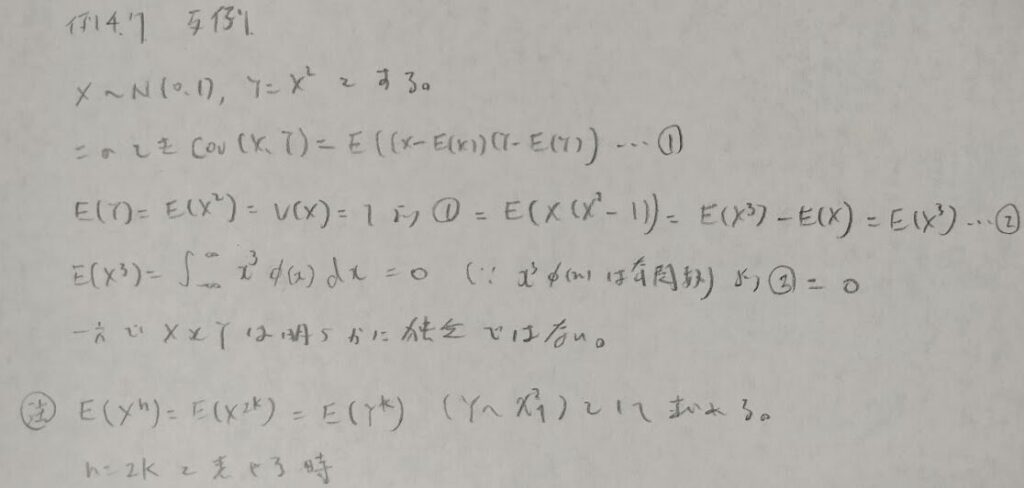
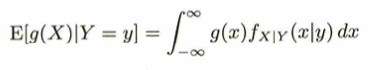
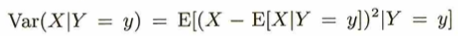
統計検定1級に頻出の繰り返し期待値の法則(つまり全期待値公式)と全分散公式についてまとめます。

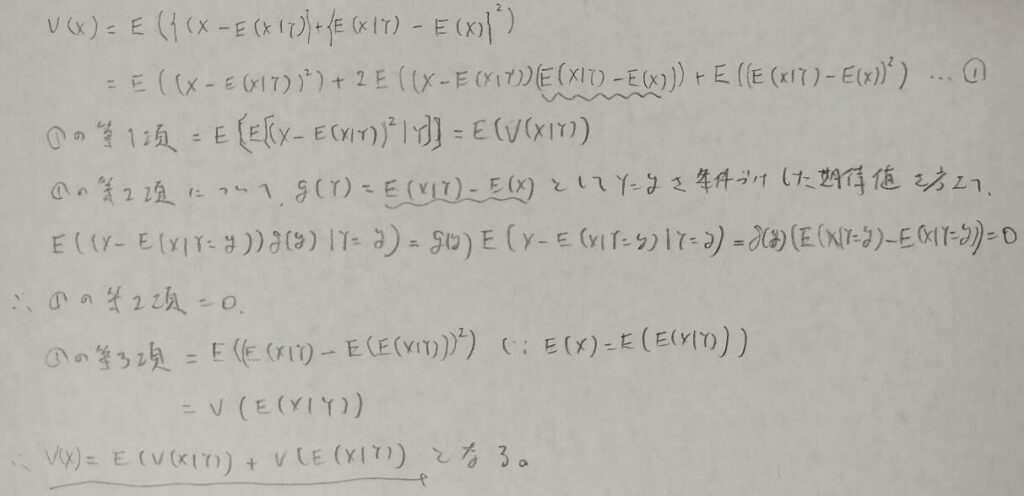
2変量正規分布の例で全期待値と全分散公式の使い方を振り返ります。
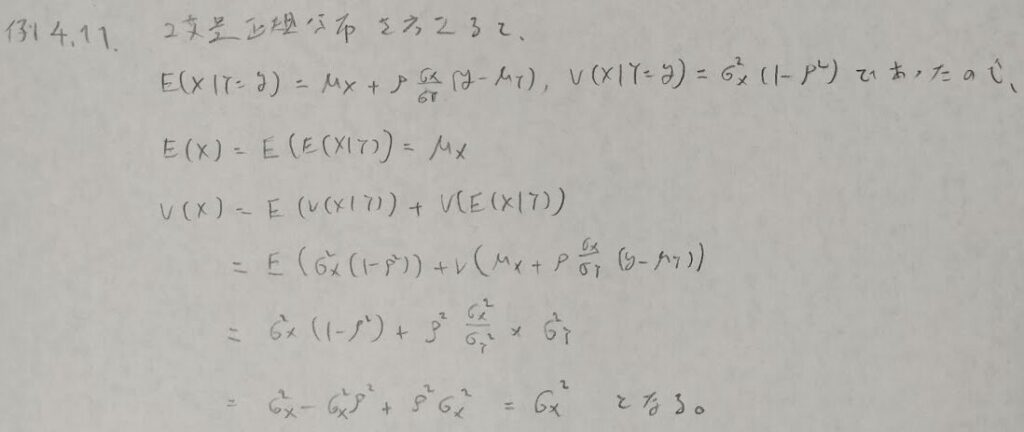
確率母関数と積率母関数では、sやtの範囲が盲点です。


『データ解析のための数理統計入門』はこのように読者にわかりやすい順番で定義や定理を展開してくれているので、学習効率が上がります。
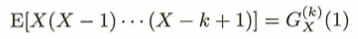
確率母関数は離散確率変数のみに使い、積率母関数は離散でも連続でも利用可能です。

この命題はかなりの盲点です。0の近傍の任意のtに対しての部分が抜け落ちていると統計検定1級では減点されそうです。0の近傍の理由はk次モーメントを求める際にtに0を代入しているところから来ていると思われます。実は積率母関数はラプラス変換に対応しています。ラプラス変換は数学検定1級の平均的な内容より難しく、大学院入試では得点分野になります。僕は『ラプラス変換キャンパス・ゼミ』を用いて学習しました。
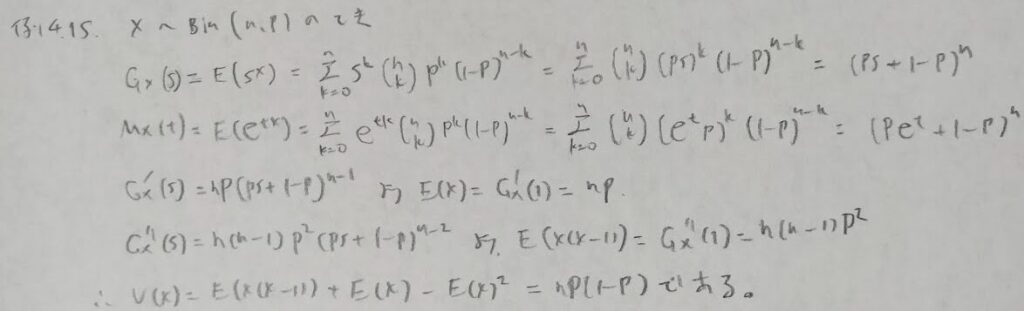
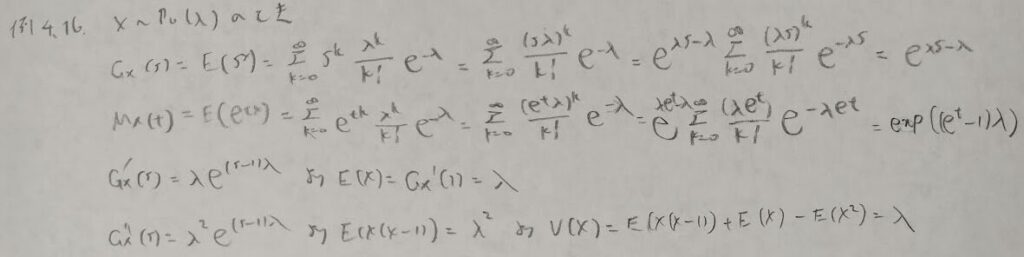
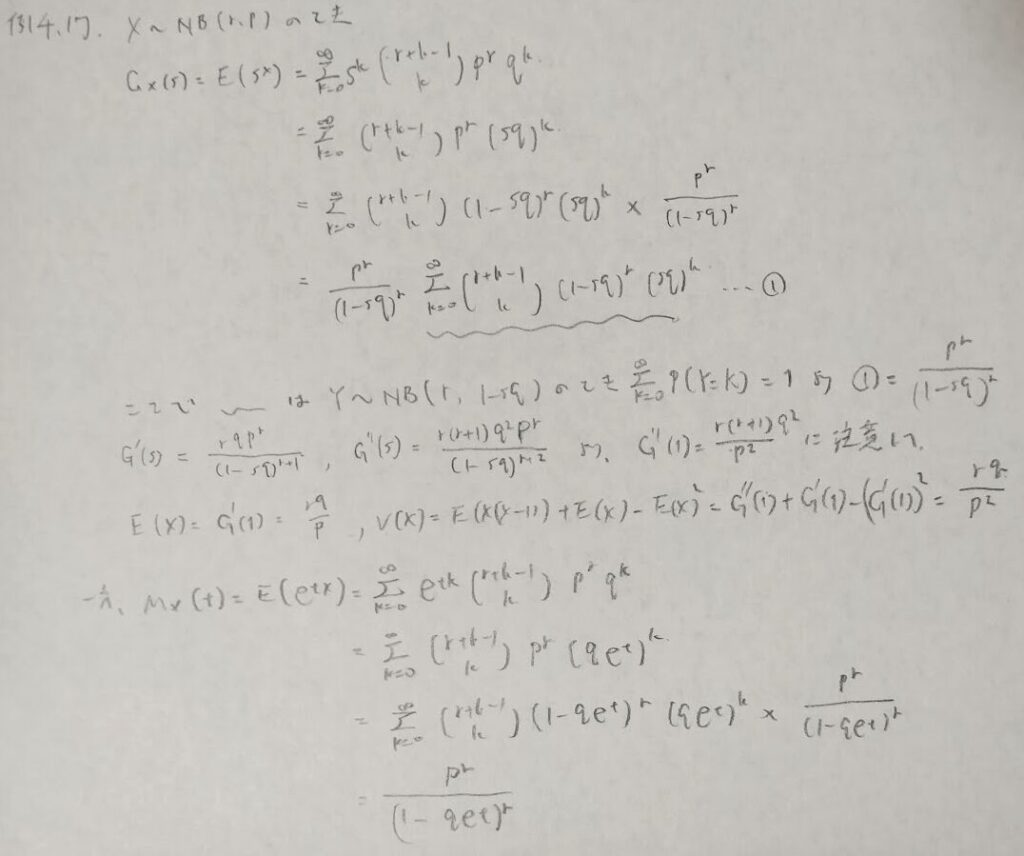
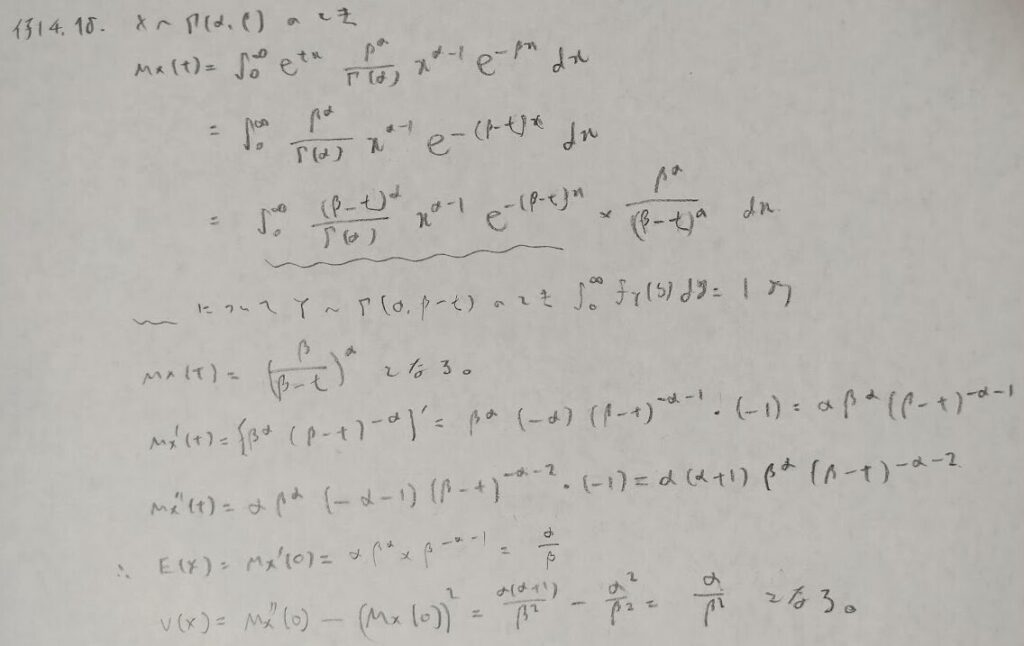
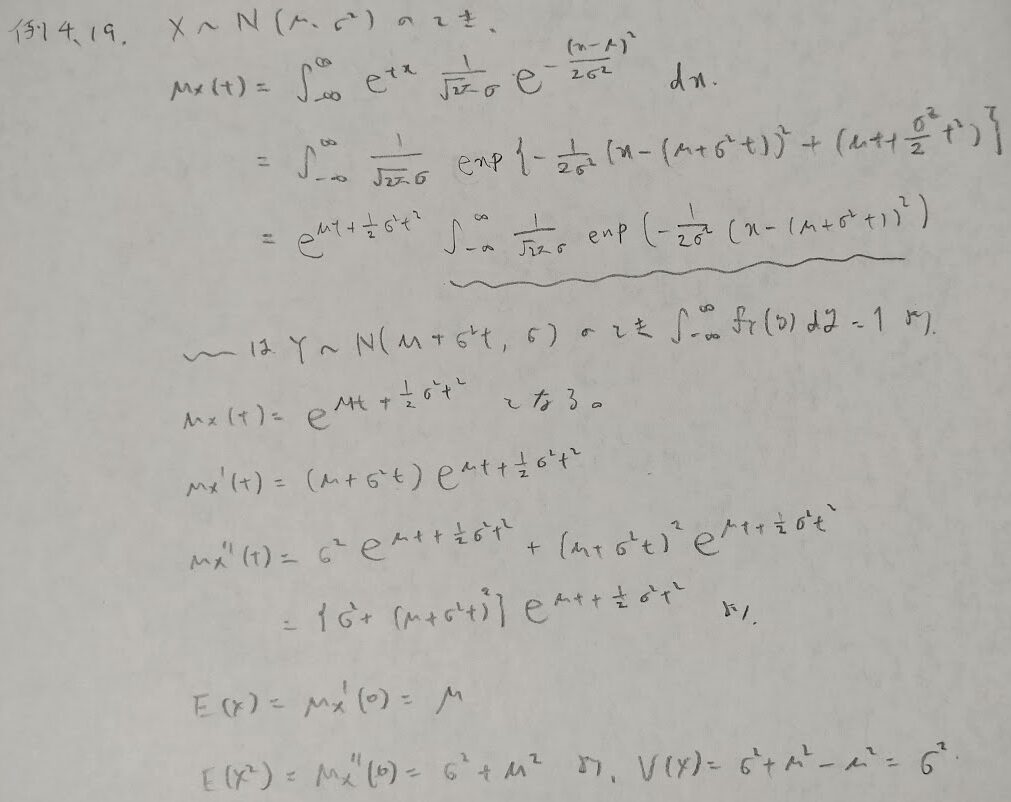
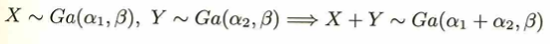
ここから多変量の分布になります。そのため1問、条件付き分布の復習をします。
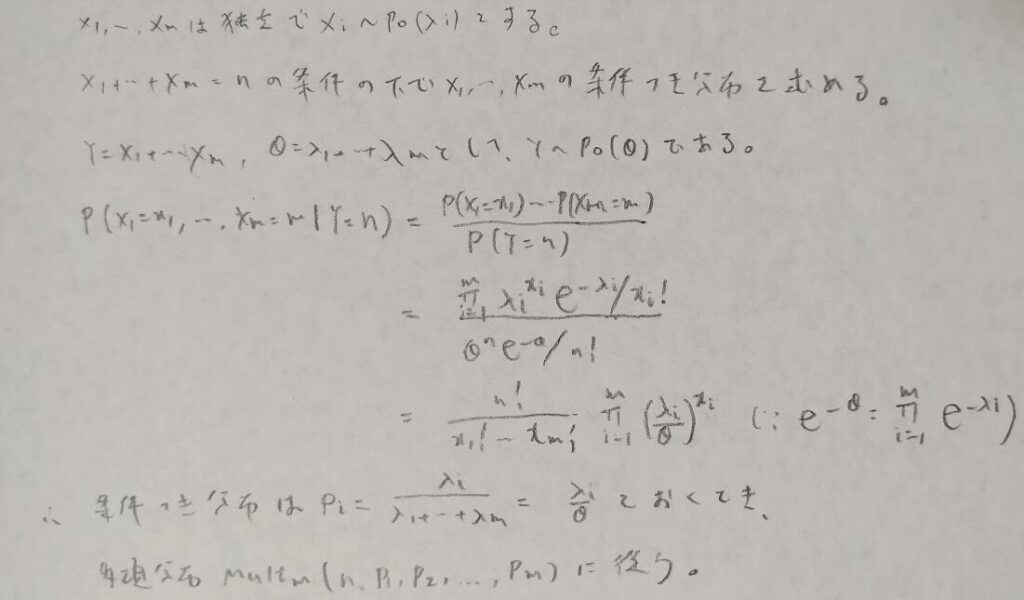
終盤は多変量正規分布に関する内容になりますが、難易度が桁違いに上がります。一般的にここの部分は難関ですが『データ解析のための数理統計入門』では体系的に書かれているので「分からない!」が減ります。しかしそれでも式変形が簡略化されている部分が見受けられますので、その部分は行間を補っていきます。
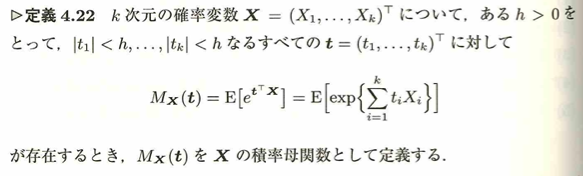
こちらも各パラメータtの条件に注意しましょう。のちの演習問題でマイナスを考慮しないことによる間違いをしてしまいました。0の近傍であることに要注意です。次にいよいよ多変量正規分布に関する性質について考えていきます。積分領域Dはk次元空間全体という意味合いで用いています。
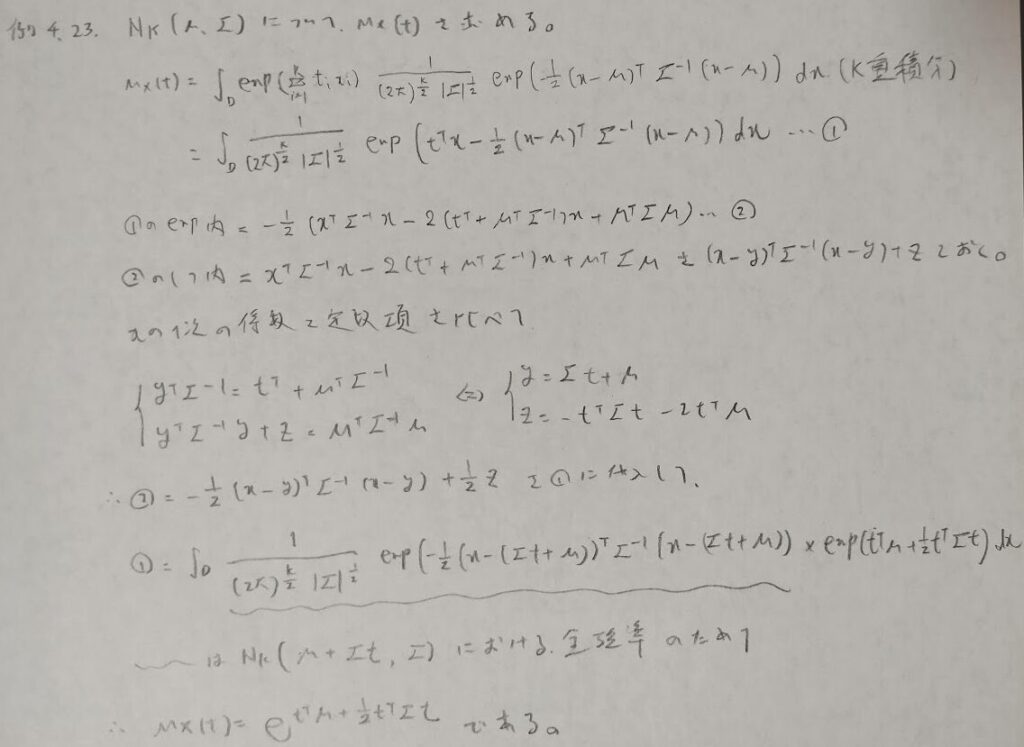

ここからは多変量正規分布の1次結合に関する内容になります。
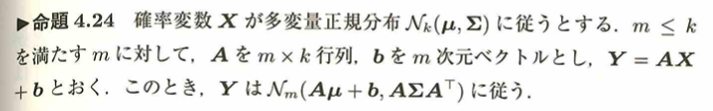
この制約がなくても行列演算はできますが、主成分分析などでの次元削減の為などでの自然な制約になっています。
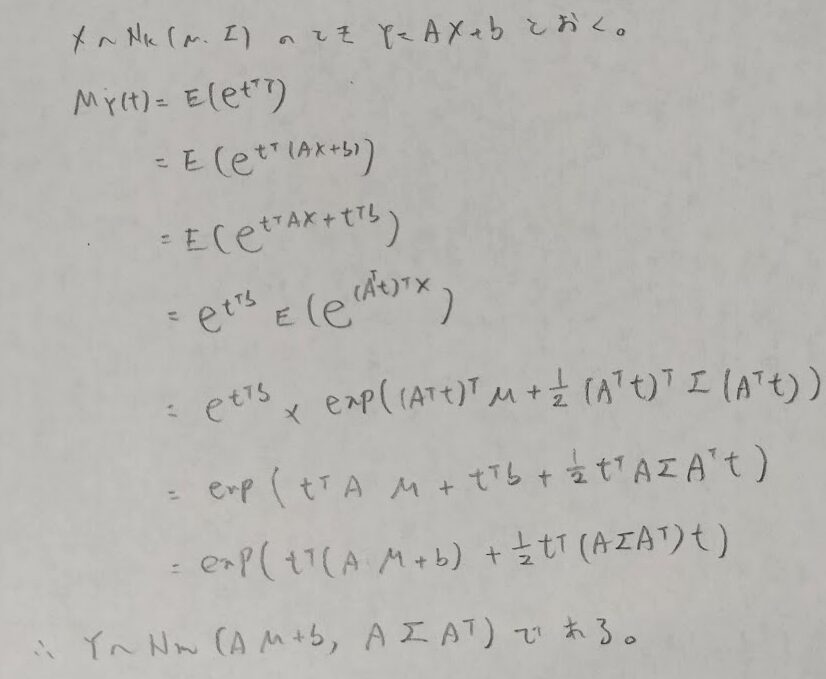
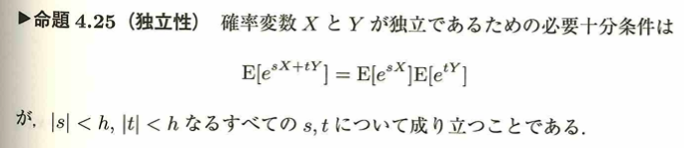
この命題の左辺はXとYの同時分布の積率母関数で、右辺はXとYのそれぞれの周辺分布の積率母関数の積になっています。すなわち同時分布がそれぞれの周辺分布の積で表現されることになるので、XとYが独立であることを言っています。次の命題は統計検定1級に出ていないので、予想問題として導出してみます。

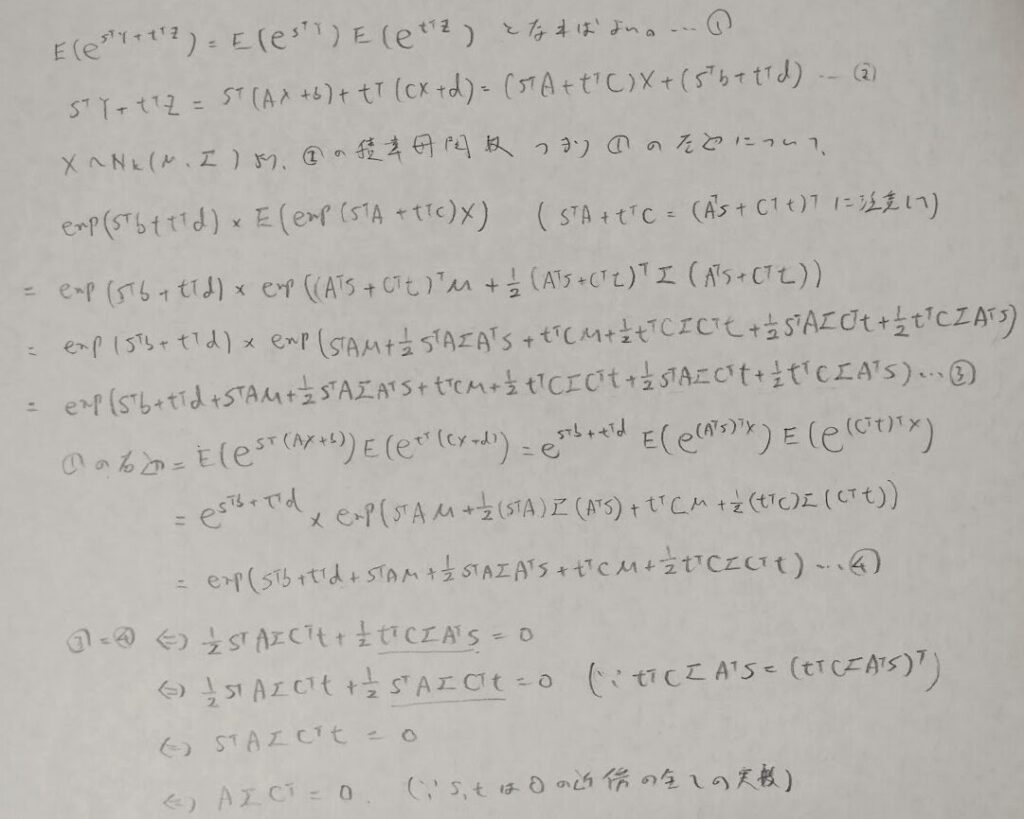
なんとか正解でしたが、とても大変な問題でした。2変数の恒等式であることがこの問題の本質です。
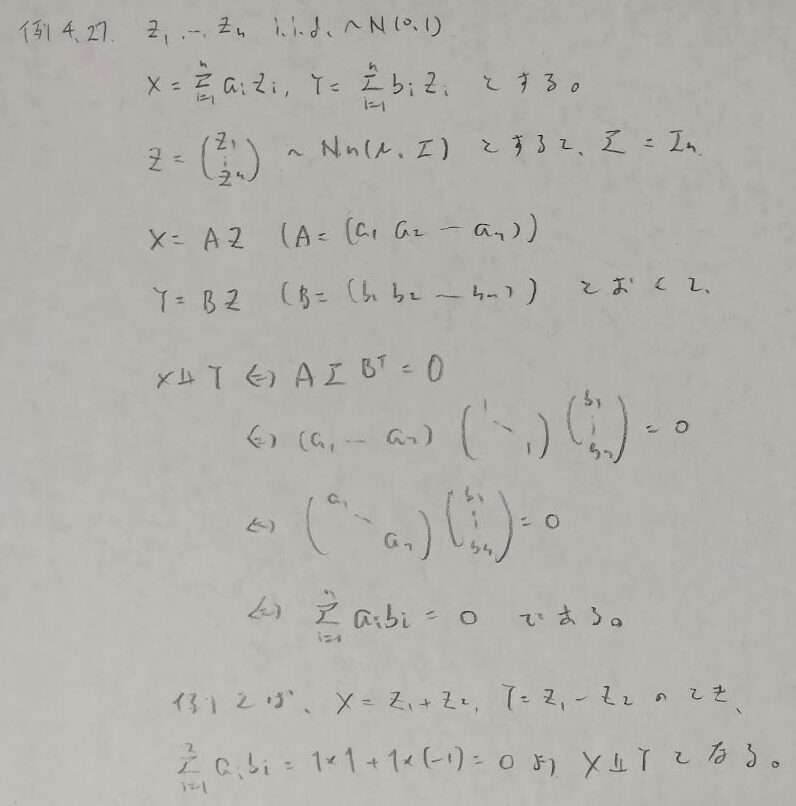
最後に積率母関数は常に存在するとは限らないため、理論での応用面ではフーリエ変換(常に存在)と同値な特性関数を用います。

統計検定1級の予想問題として使える演習問題
『データ解析のための数理統計入門』の第4章の演習問題を順に解いていきます。久保川先生の模範解答と答えは一致していますが、自力で解いた問題がほとんどのため途中計算や考え方が異なる場合があります。1つの回答例としてご活用ください。
歪度と尖度
問1からすごい計算量になりますので、小問で分割しました。

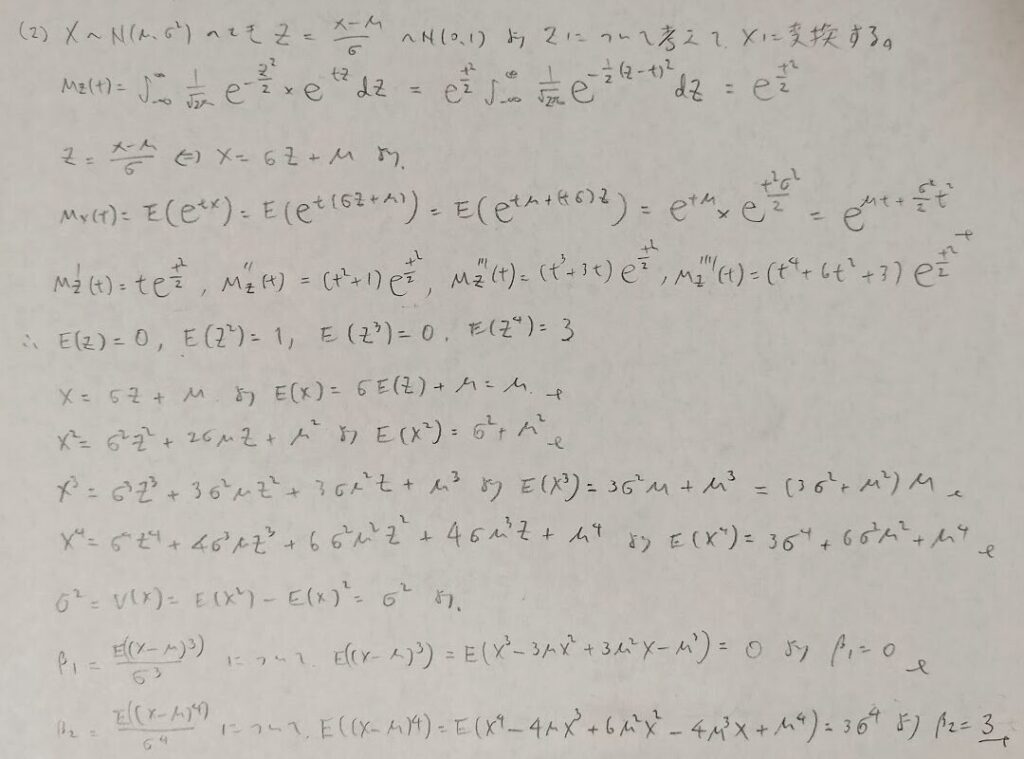
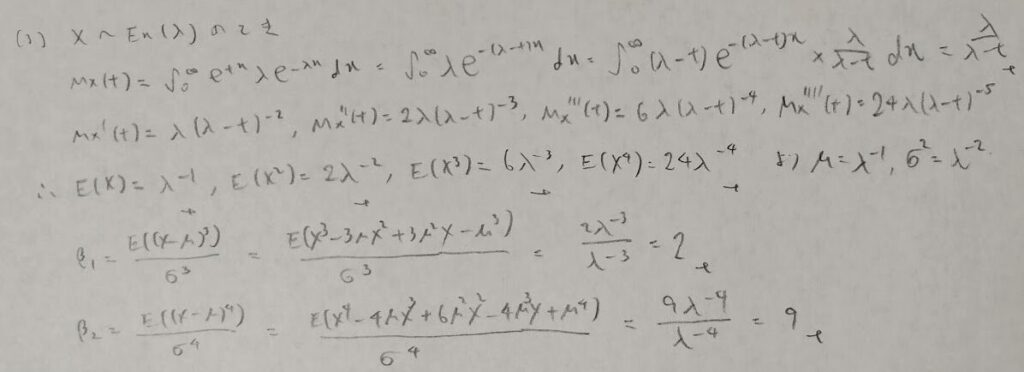
多項分布とその共分散

多項分布の共分散はアクチュアリー数学で頻出なので覚えておいた方が良いです。
ポアソン分布の全確率1の利用問題
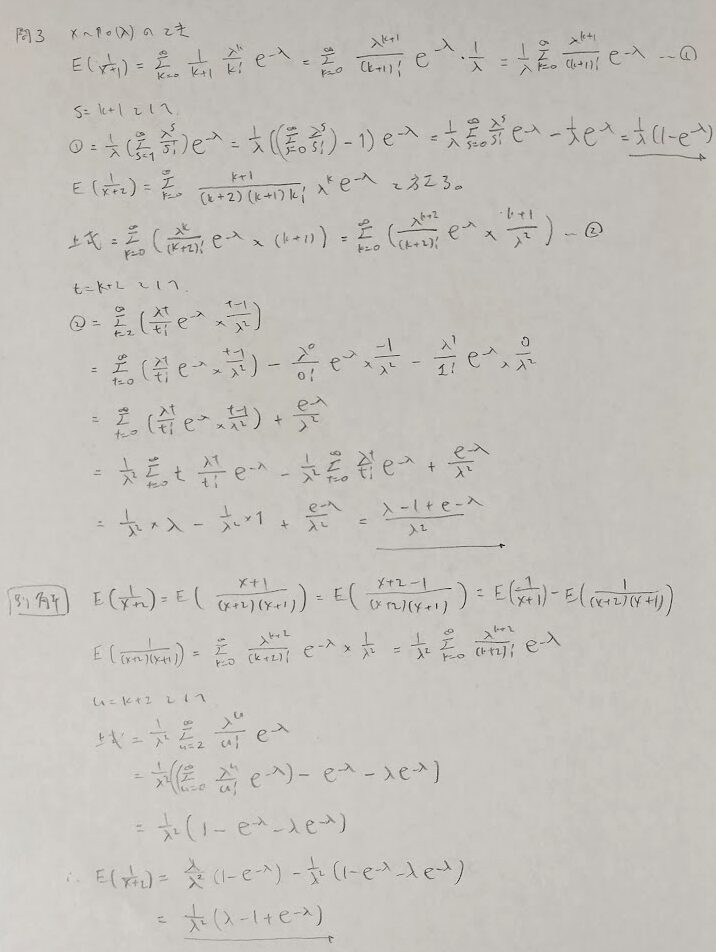
分布関数とメジアン
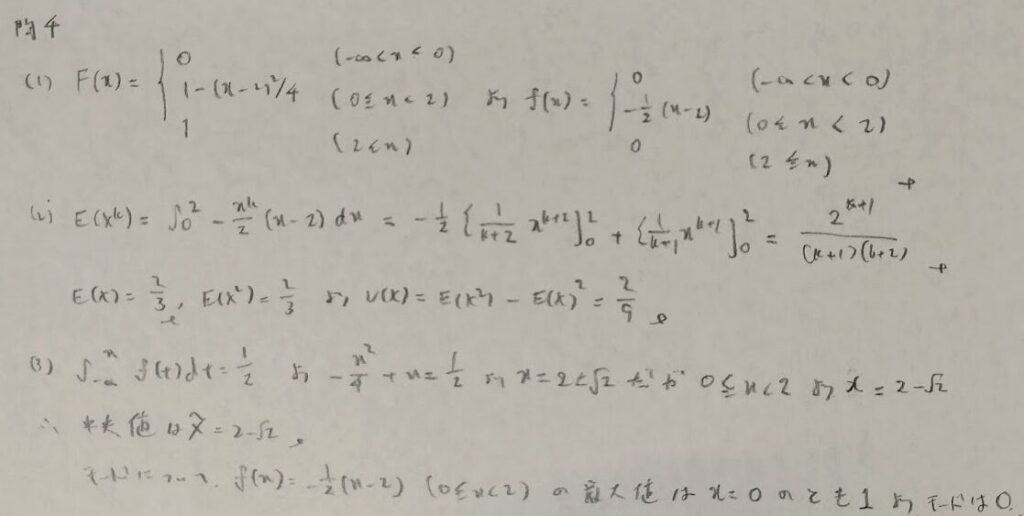
確率密度関数において1点の意味で重要なのはモードを求める時くらいなのかもしれません。
指数分布とチェビシェフの不等式
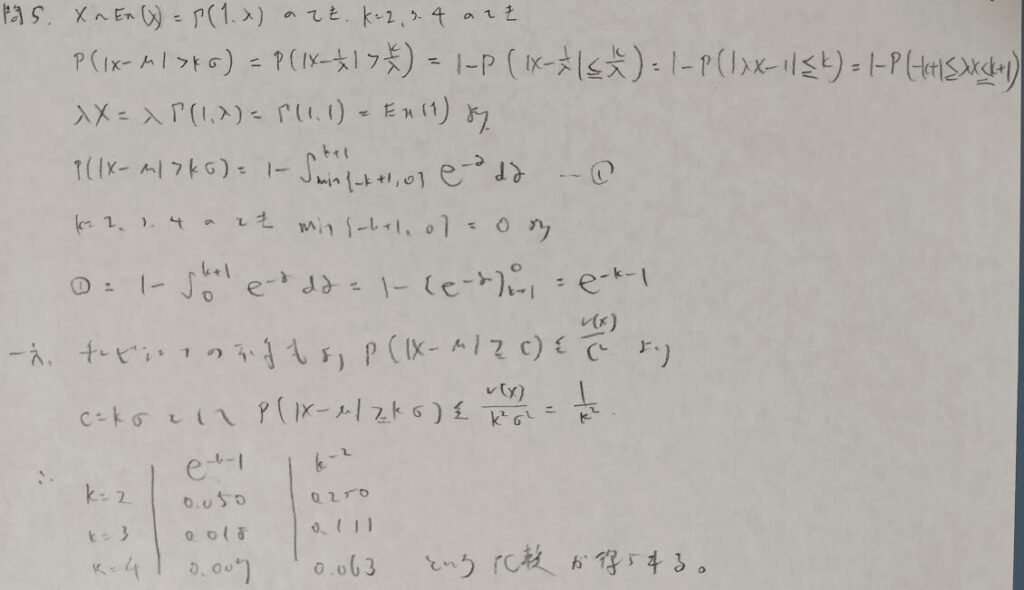
しっぽ確率(離散)
しっぽ確率の問題は統計検定1級の2024年に出題されました。ほぼ同じ問題です。下の問7と合わせて何も見ずに導けるようにしておきたいですね。
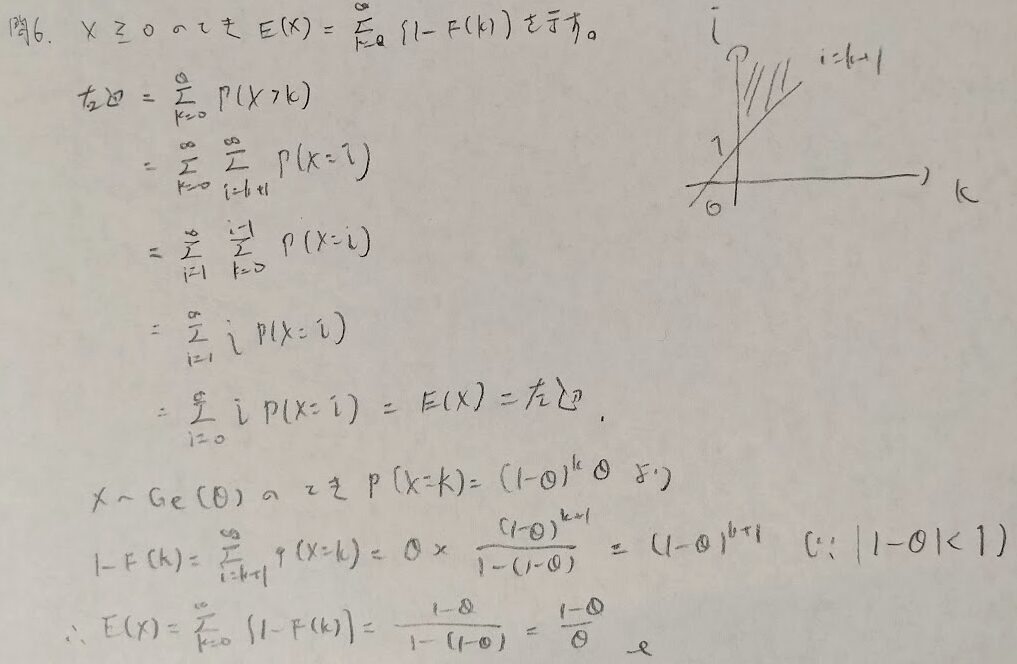
しっぽ確率(連続)
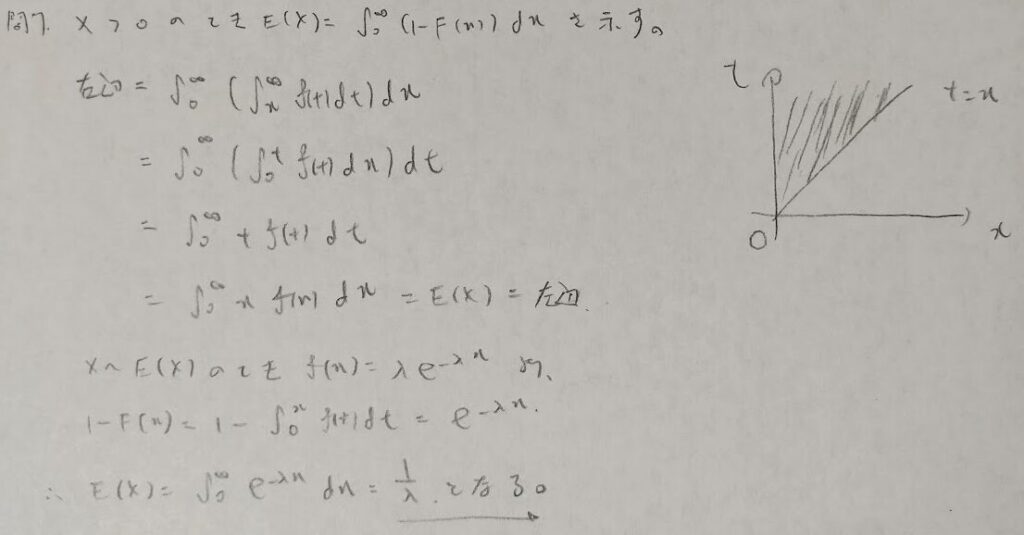
2024年の統計検定1級の受験時は『データ解析のための数理統計入門』をやりこんでいなかったので、ほぼ同じ問題が出てきても気づかずにスルーしてしまいました。『データ解析のための数理統計入門』がとても大事な参考書だということを再認識しました。
打ち切り分布

対数正規分布

一様分布の問題
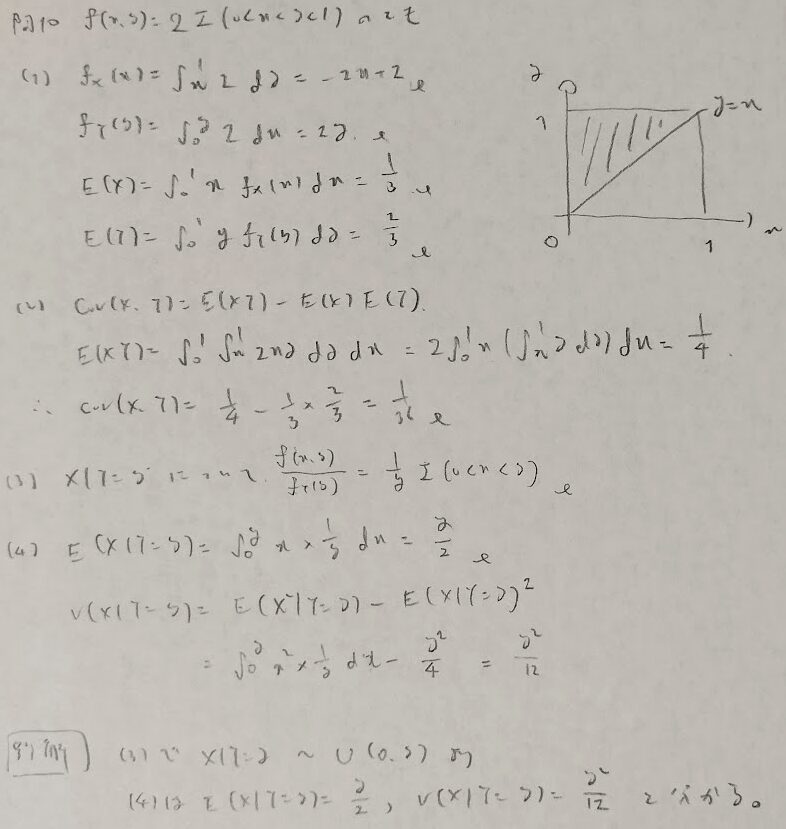
コーシーシュワルツの不等式
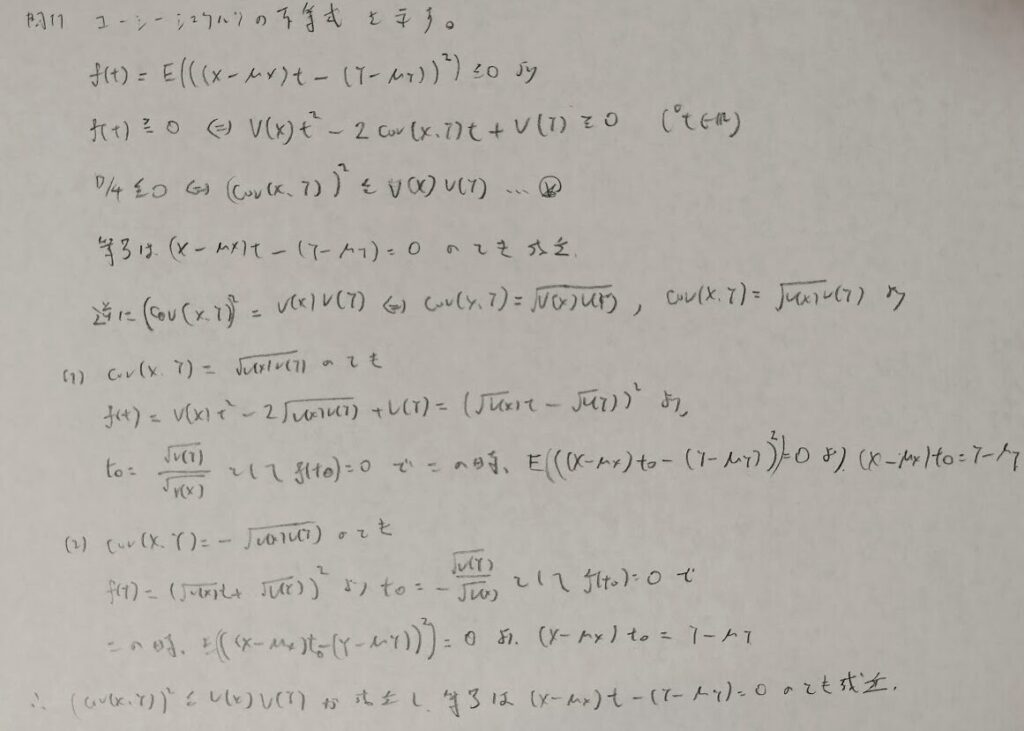
条件付き分布の難問
本章最難関と言っても良いです。わからなくて模範解答を見ました。

一様分布の簡単な問題
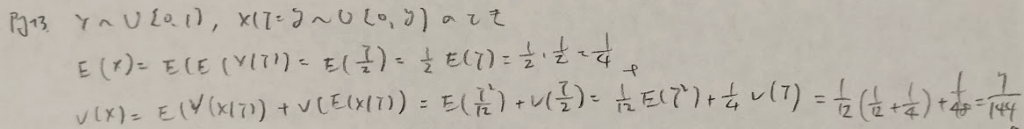
独立に注意
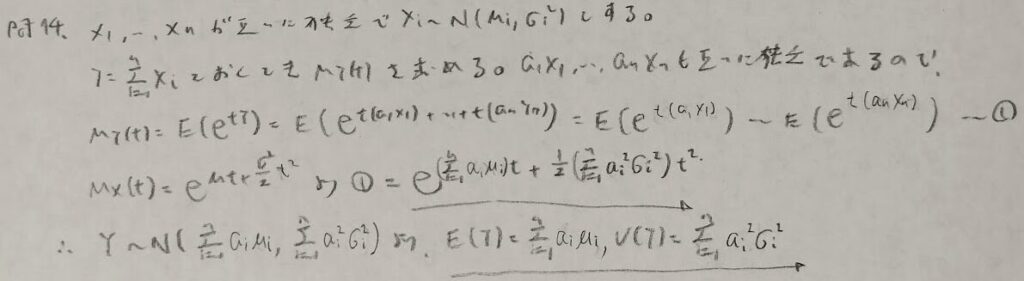
ディリクレ分布と周辺分布の期待値
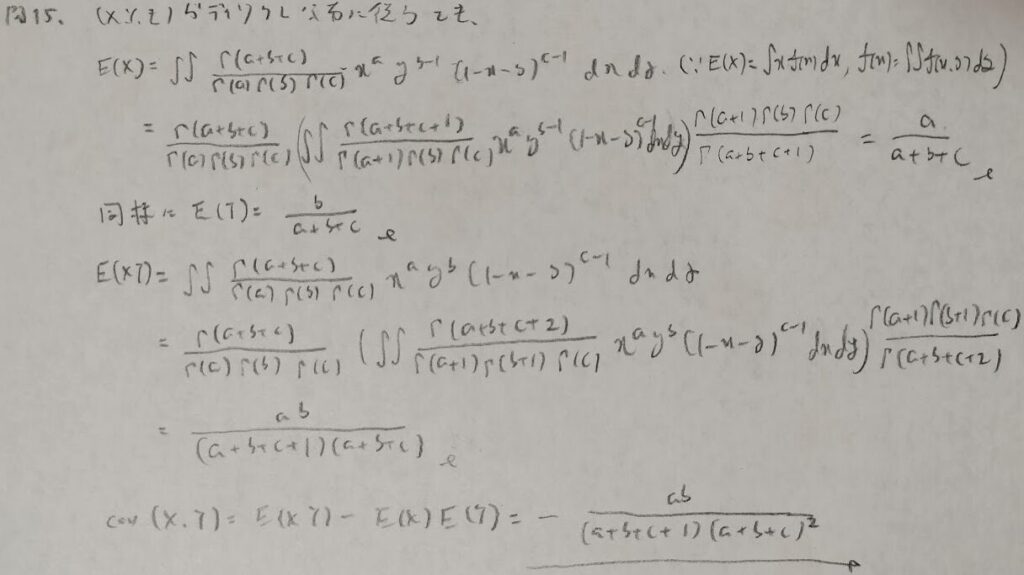
共分散でマイナスがつくのは、多項分布と似ています。多項分布やディリクレ分布(ベータ分布の拡張版)では、Xが増えると制約条件に従ってYが減っていくため、マイナスがつくのだと考えます。
多変量の積率母関数
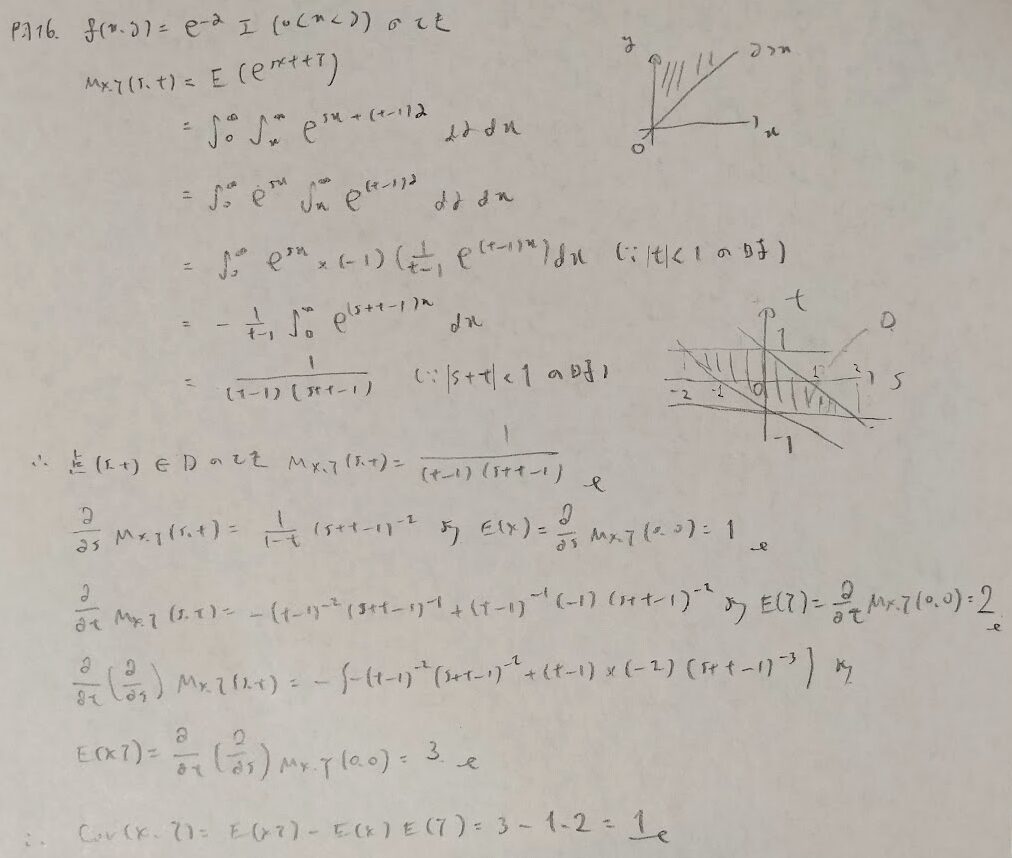
確率ベクトルと共分散
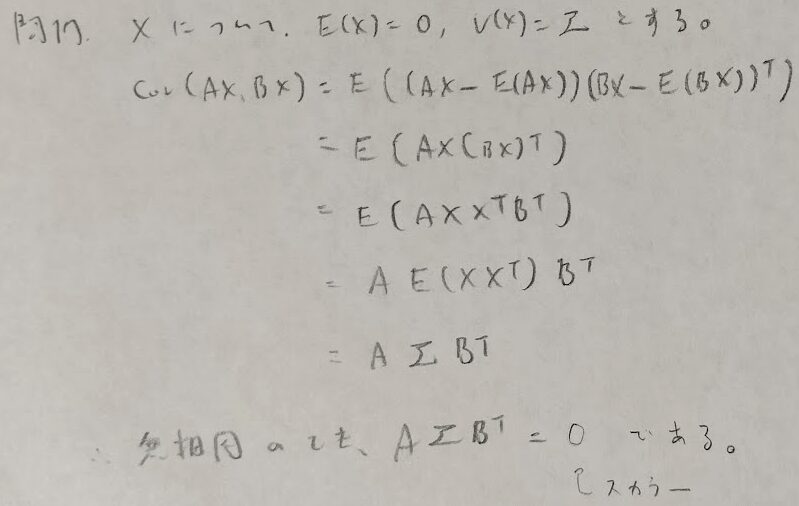
ここら辺の問題は類書での掲載が乏しく『データ解析のための数理統計入門』の問題のチョイスの素晴らしさが際立ちます。
無相関の証明
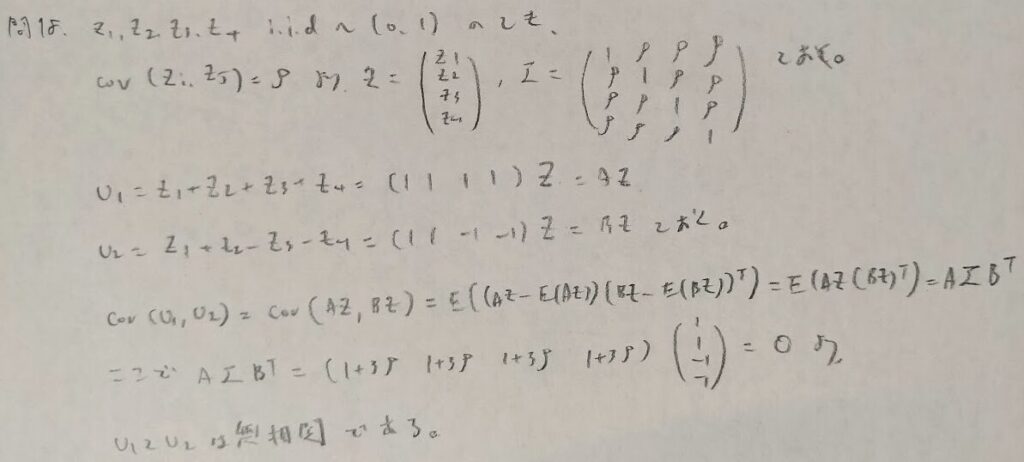
この問題は前問の具体例です。ただし統計検定1級の本番を想定してヒントが使えない状況を想定した答案にしました。
1という行列の利用
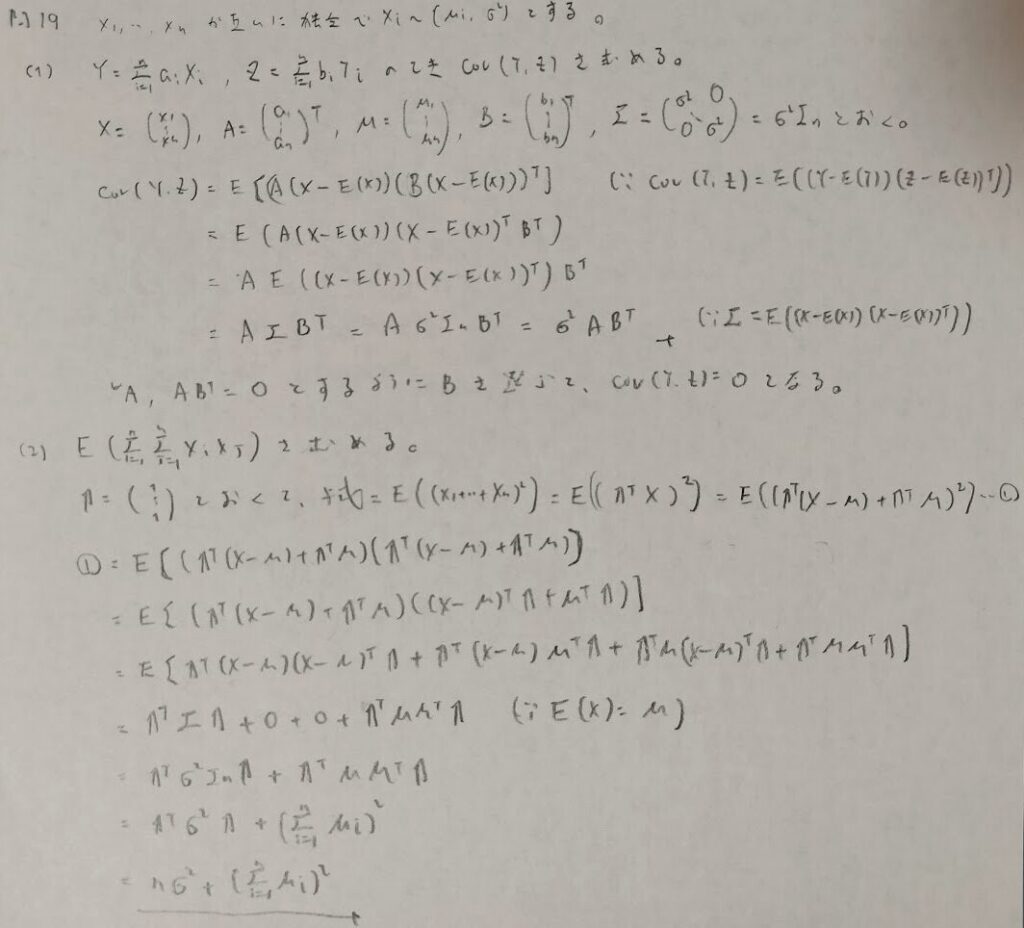
良問が続く中でのさらに際立つ良問です。行列で考えることの素晴らしさを体感できます。ちなみに類題が2024年の統計検定1級の人文科学にて似た考え方をする問題がひっそりと出題されました。「1」という行列を用いるMDSの問題です。
正規分布の積率母関数の応用問題
この問題の後半は積分の嵐です。自力で解くためには相当の鍛錬が必要です。
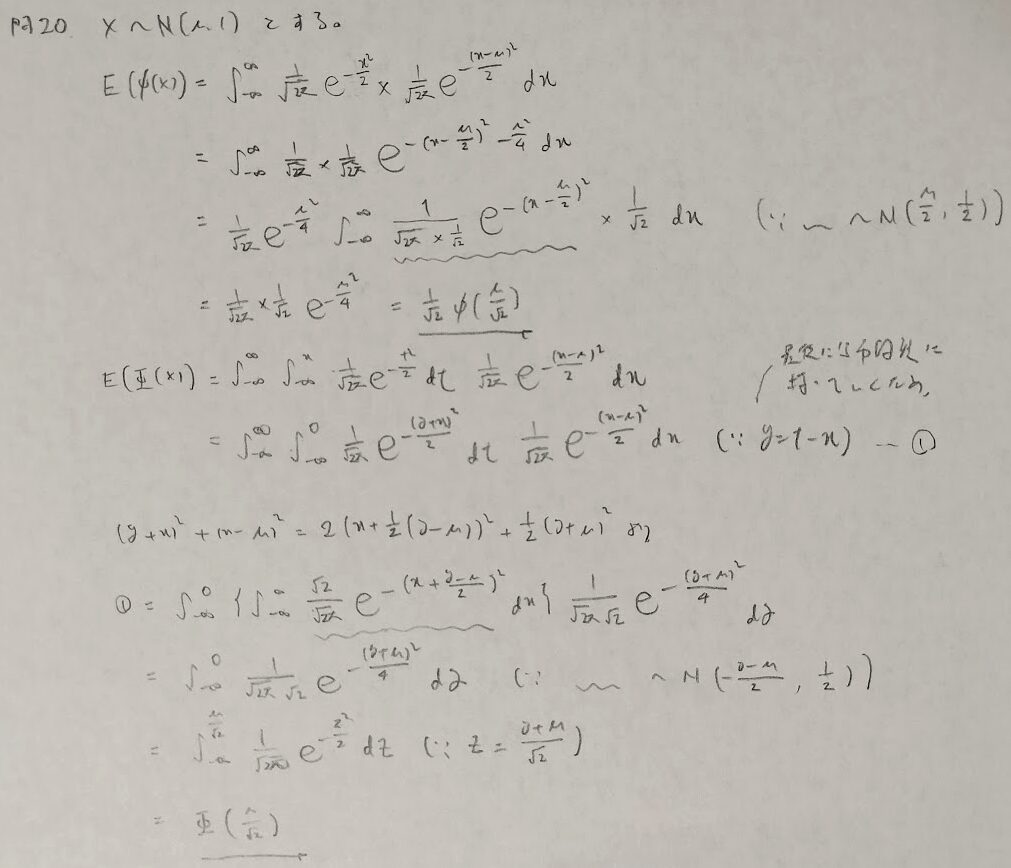
平均2乗予測誤差の最良予測量
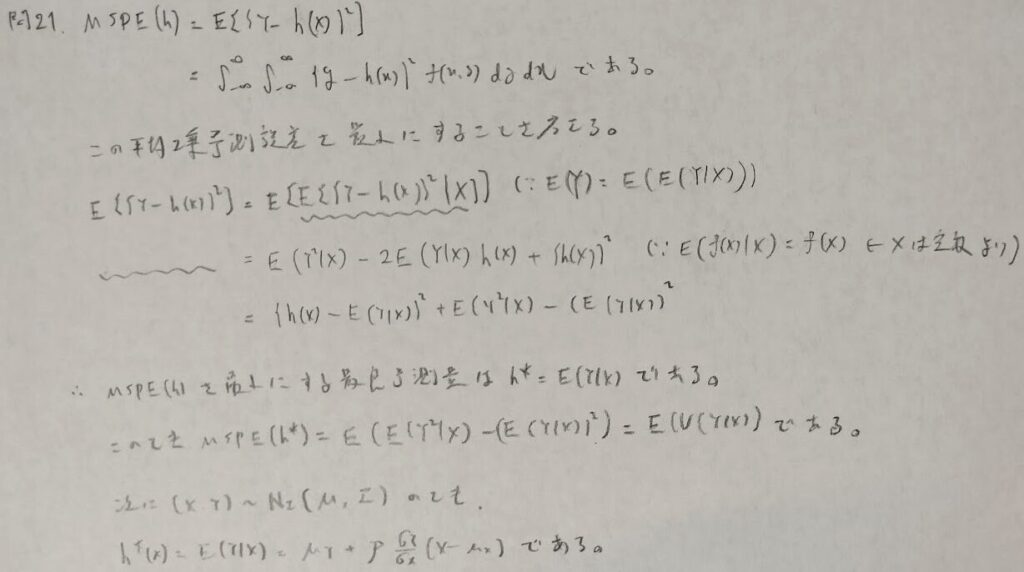
最後の問題で見慣れた結果が出てきて安心しました。
『データ解析のための数理統計入門』はさらにここから良問だらけになってきます。一緒に1問1問1を追って学習していきましょう!