統計検定1級の対策書として公式本以外で真っ先に買うべき本である『データ解析のための数理統計入門』の第6章の解説と演習問題を自力で解いた学習の軌跡の記事です。特に本章は極限関係の内容を基礎本的な箇所からデルタ法までとても分かりやすく体系立てた解説で、スッと頭に入ってきます。今までの章の中で、演習問題を含めて特におすすめできる内容です。
マルコフの不等式→チェビシェフの不等式→大数の法則→確率収束→分布収束→中心極限定理→連続写像定理→デルタ法→分散安定化変換の流れを数おページにバランス良く取り入れている凄い本です!
統計検定1級青本の第6章の説明と例題
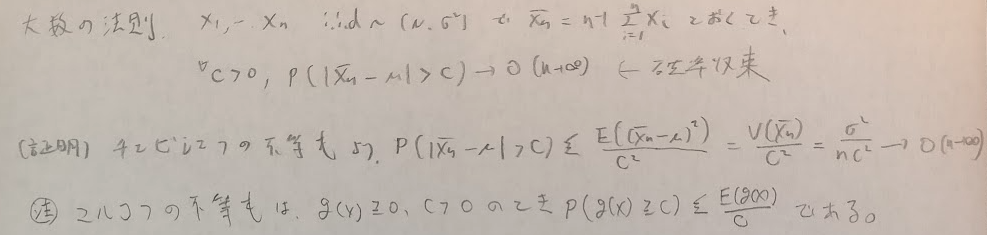
マルコフの不等式→チェビシェフの不等式→大数の法則という順番です。マルコフの不等式はこちらで解説しています。
大数の法則は確率収束の考えに通じます。確率収束を示したい時は平均2乗収束を示せばOKです。もちろん照明も入れておきます。

大数の法則は積分計算の近似としてモンテカルロ積分を適用する際に大活躍します。積分計算の結果を保証するために大数の法則があります。

次に中心極限定理に移ります。分布間の話になるので分布収束を導入します。

細かいことを置いておくと、連続性定理とは積率母関数が収束→分布関数も収束という内容です。次の例ではポアソン分布において中心極限定理が成り立っていることを示しています。
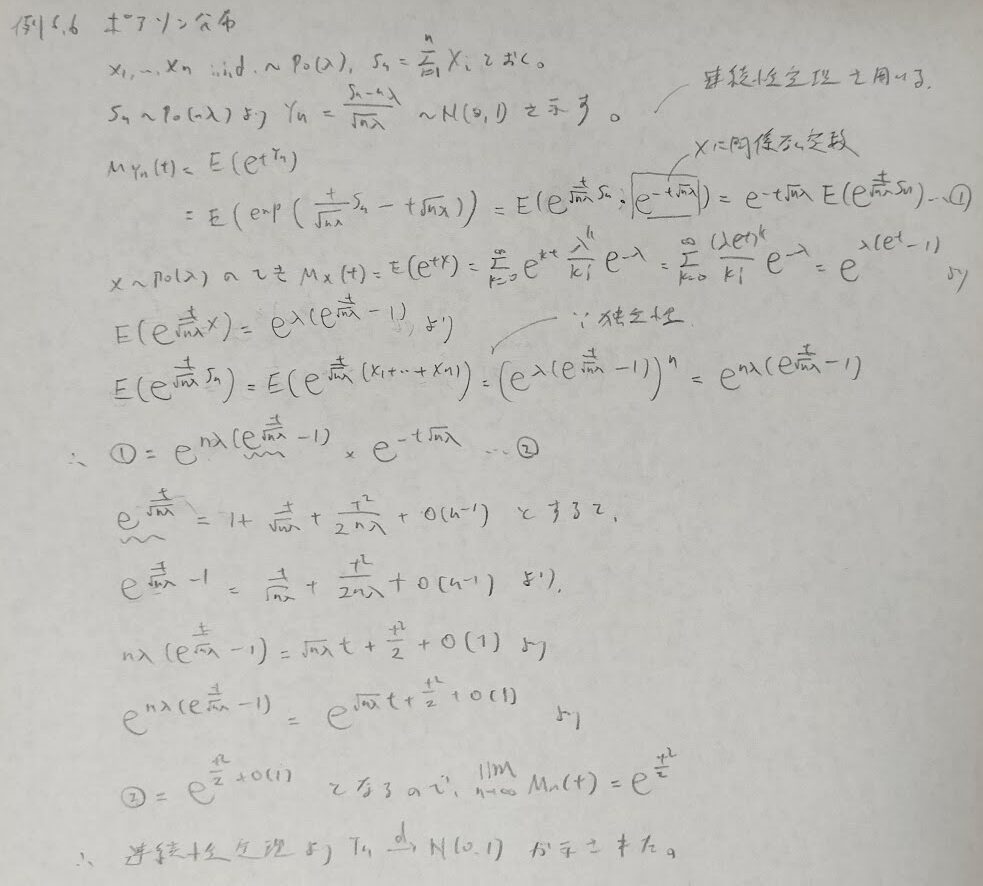
証明の核の部分はテイラー展開でした。またランダウのスモールオー記号も活躍します。次は実際の中心極限定理を証明します。これは後に行うデルタ法の仮定部分に相当する箇所になります。
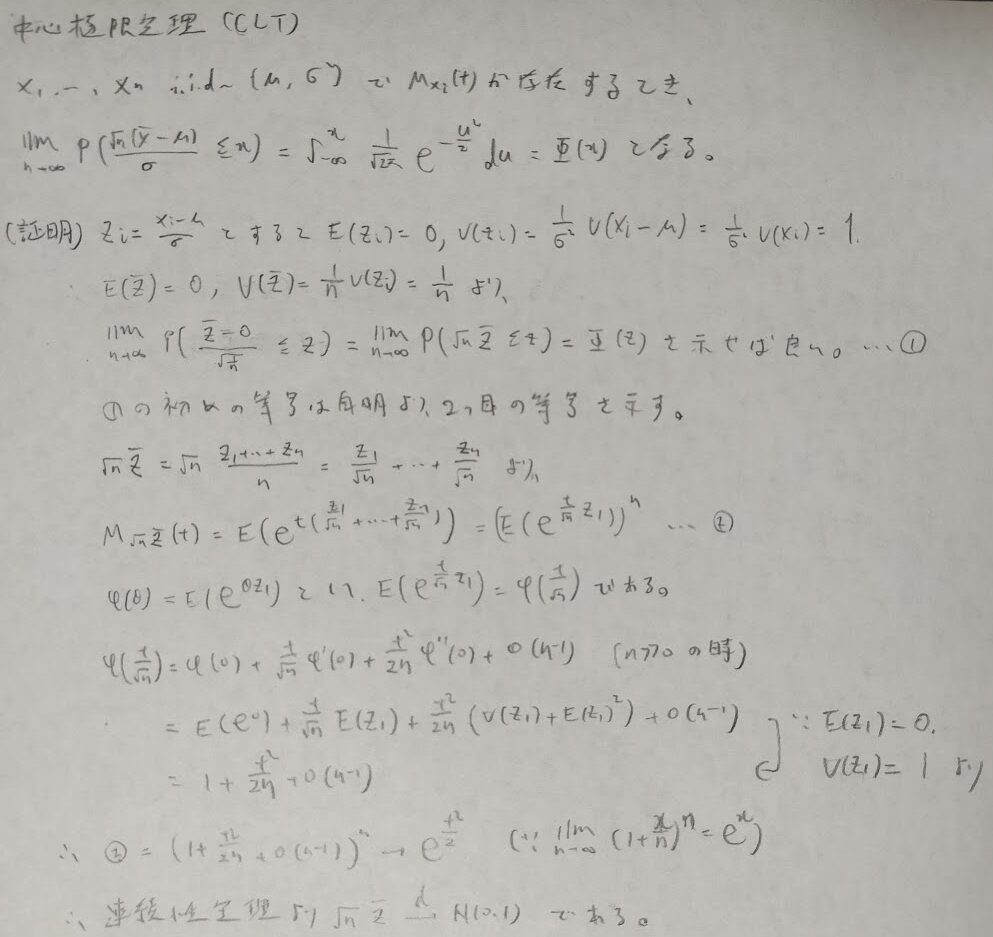
先ほどのポアソン分布の問題を一般化した感じです。次は実際に二項分布において中心極限定理を適用した場合に近似が良くなる方法である連続補正についてです。こちらはQC検定1級の方が深く突っ込んだ内容になっています。
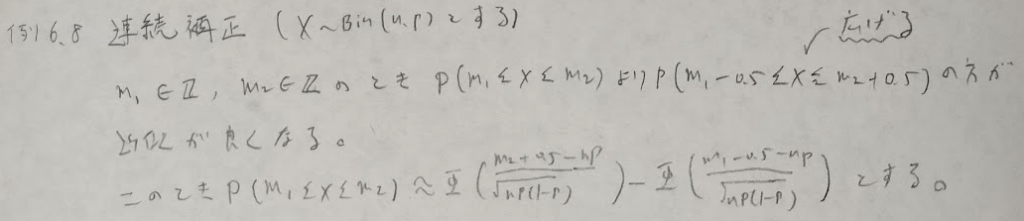
極限についての重要な応用例としてデルタ法があります。『データ解析のための数理統計入門』ではデルタ法に行くまでの話の流れが完璧だと思っています。学習していて今までの内容が一つに繋がっていると感じて感動しました。

実際にデルタ法を適用する具体例がベルヌーイ分布+ロジット変換というQC検定1級に出てくる公式の証明になっていることが『データ解析のための数理統計入門』の解説の質の高さを際立たせています。
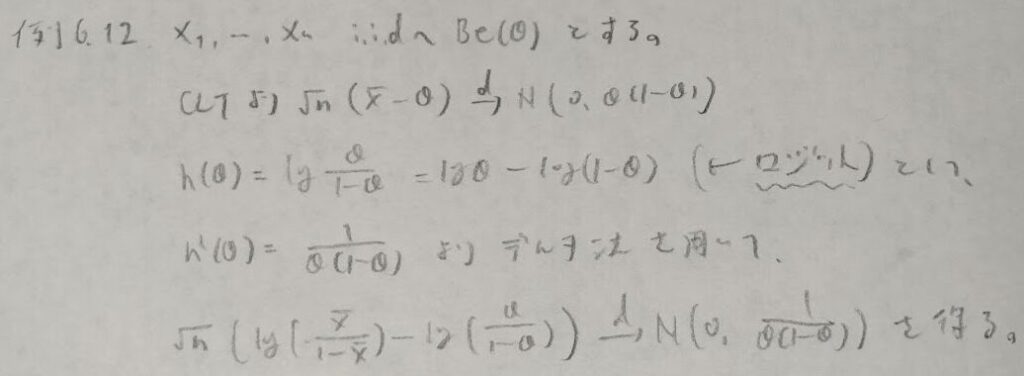
統計検定1級青本の第6章の演習問題の解説
問1:平均2乗収束→確率収束
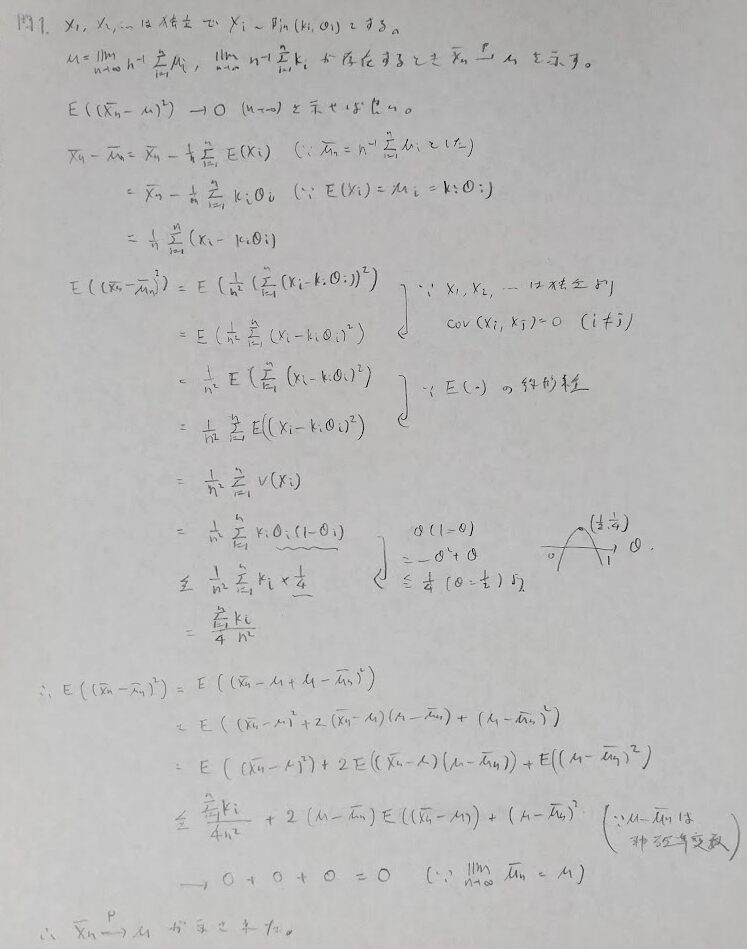
問2:正規分布とモンテカルロ積分とCLT
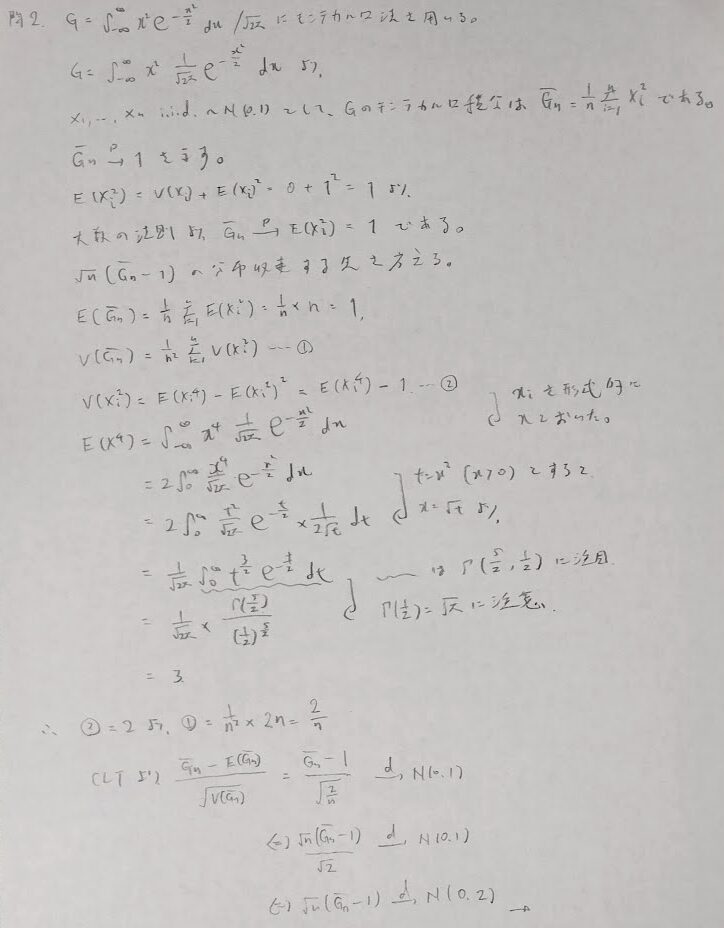
本問はいろんな観点から考えないと最後の答えまでいけないので、とても良い問題です。特に標準正規分布における高次モーメントの出し方がわからないと(覚えていないと)詰んでしまう問題なので、一般化をしてみました。
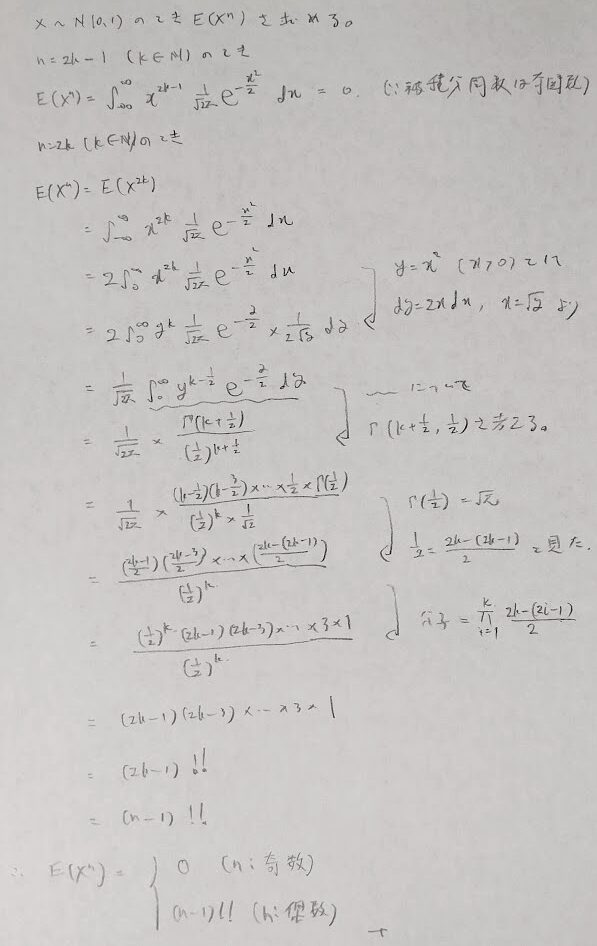
ちなみに2乗階乗は偶数の場合は0までかけずに2まででストップします。通常の階乗と同様に0!!=1とし、そして(-1)!!=1とします。
もしnが偶数の場合に0まで掛け合わされていたらnの偶奇によらずにn!!とできましたが、仕方ないですね笑
問3:一様乱数の利用

本問はアクチュアリー数学におけるシミュレーションの内容(逆関数法の一例です)であり、統計検定1級にも類題が出題されています。この問題は1問として扱っていますが、実際の試験では何問かに分割されて出題される形式になる傾向があります。
問4:経験分布関数と二項分布
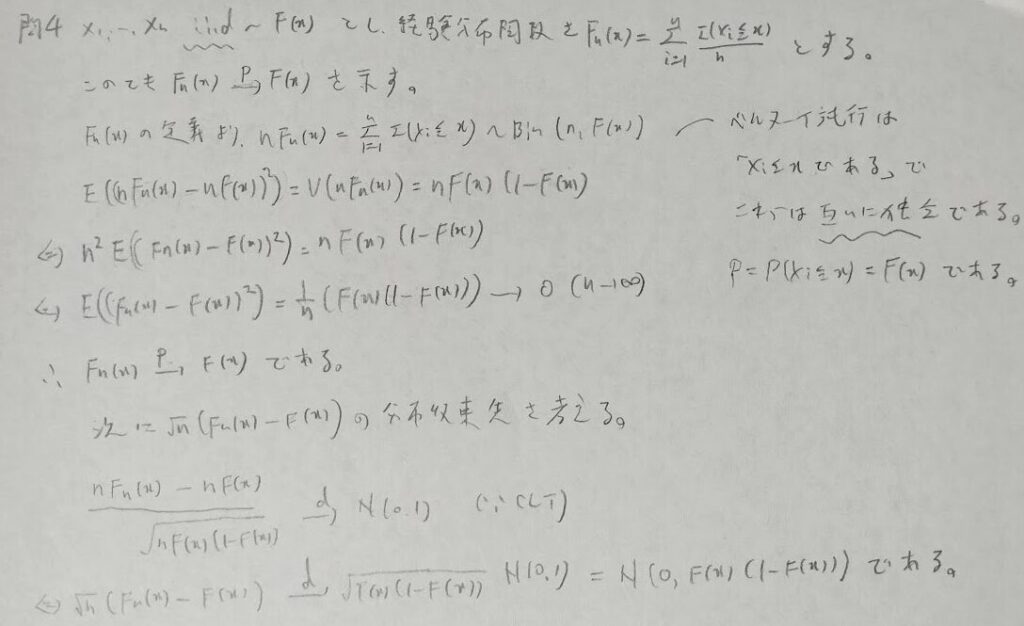
この問題はかなりの良問ですが類書にはあまり掲載されていない問題です。統計検定1級に出てもおかしくないレベルです。
問5:負の二項分布と漸近分布
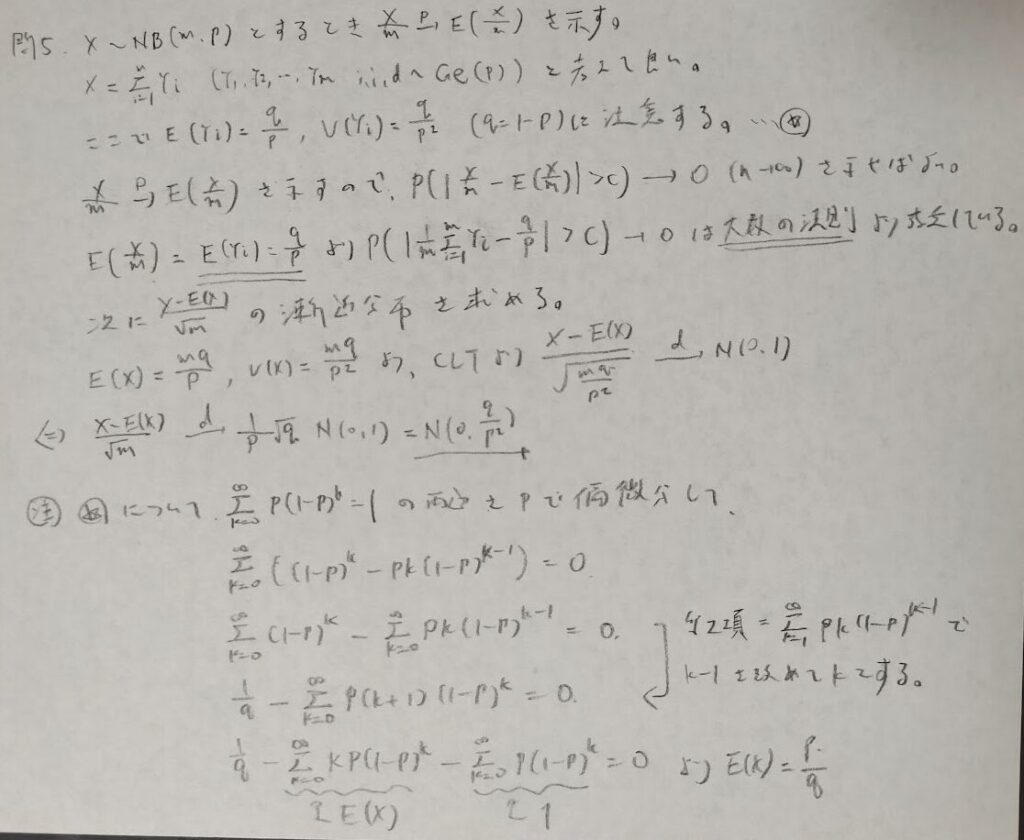
問6:積率母関数を用いた少数の法則
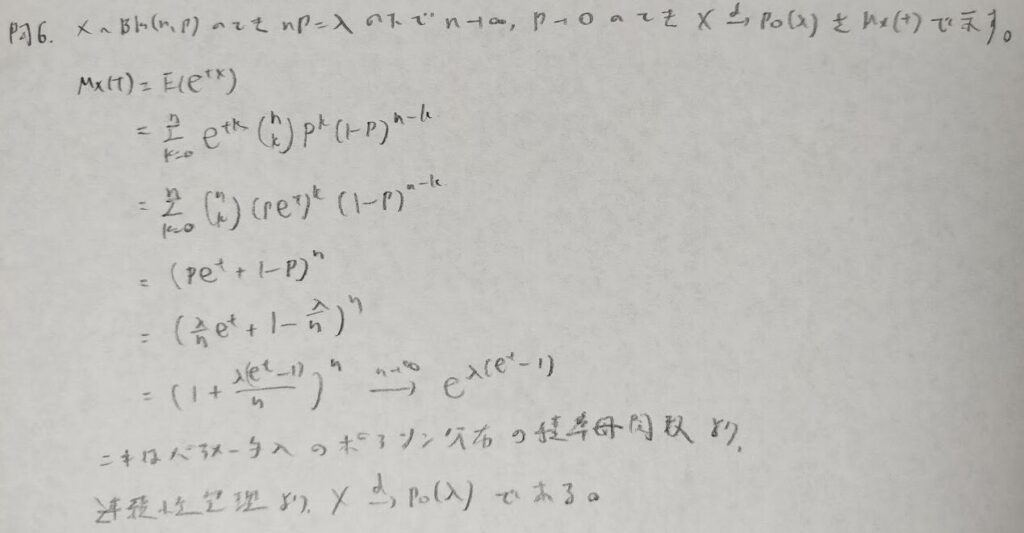
問7:中心極限定理
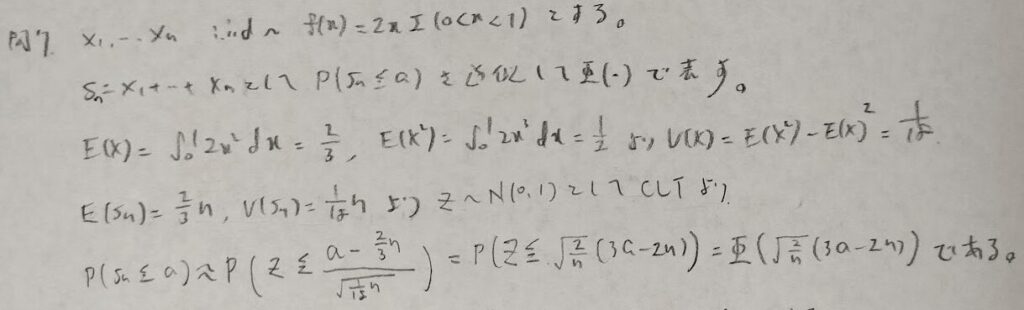
問8:分散安定化変換

分散安定化変換の問題は有名ですが統計検定1級では頻度が低いです。
問9:標準分散の確率収束先
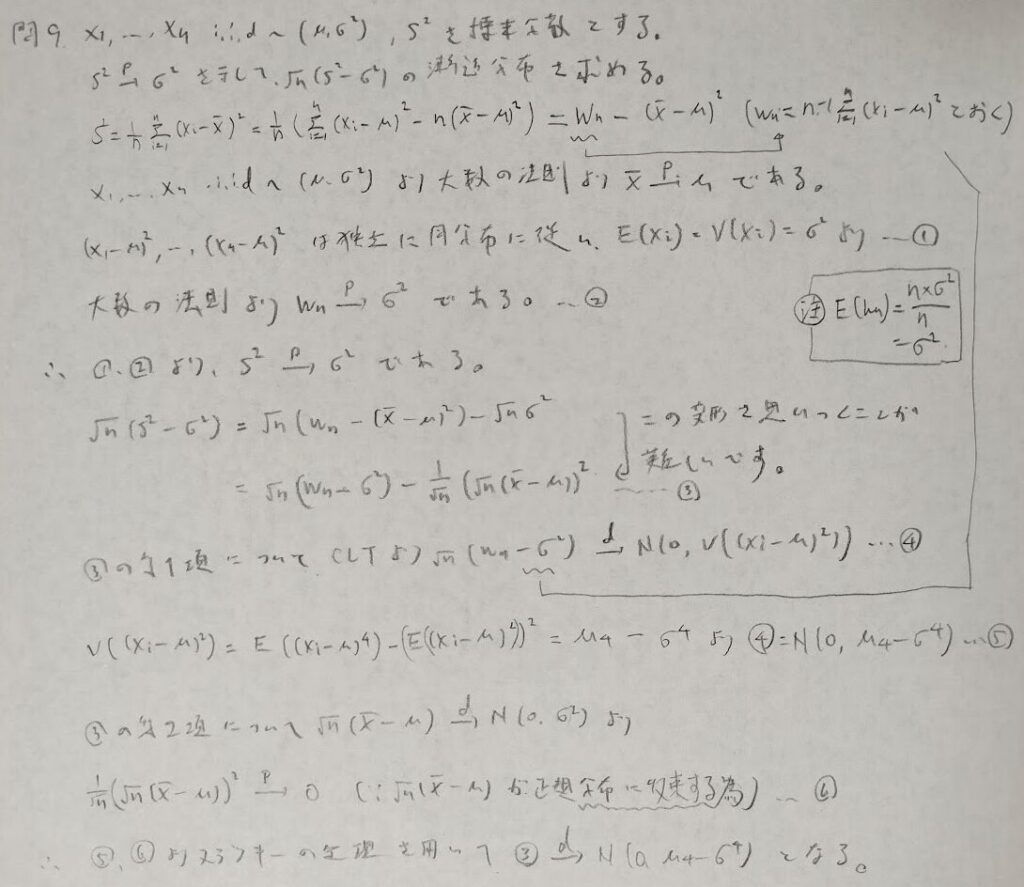
難しい問題でした。ただし有名な事実のため証明できるようになっておきたい良問です。特に最後の下から2行目の箇所が珍しい考え方です。
問10:最大統計量と漸近分布
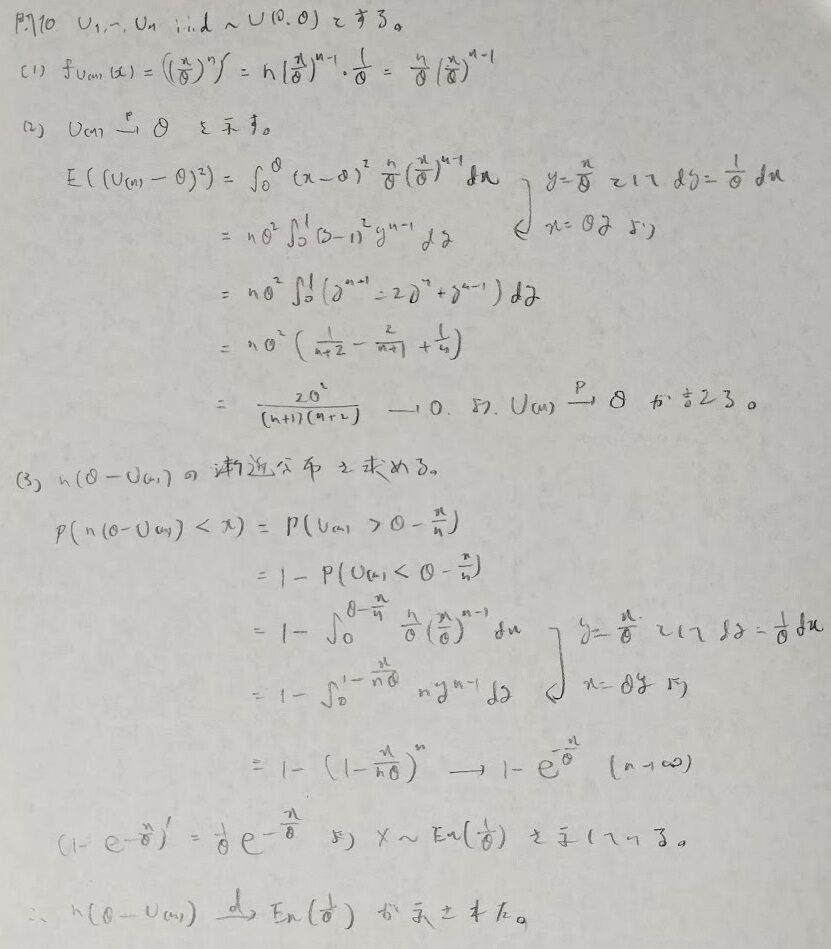
(3)の考え方がポイントです。漸近分布が従う密度の分布関数を求めています。著者の模範解答では逆の不等号からスタートしていましたが本質は変わりません。
問11:一様分布と漸近分布
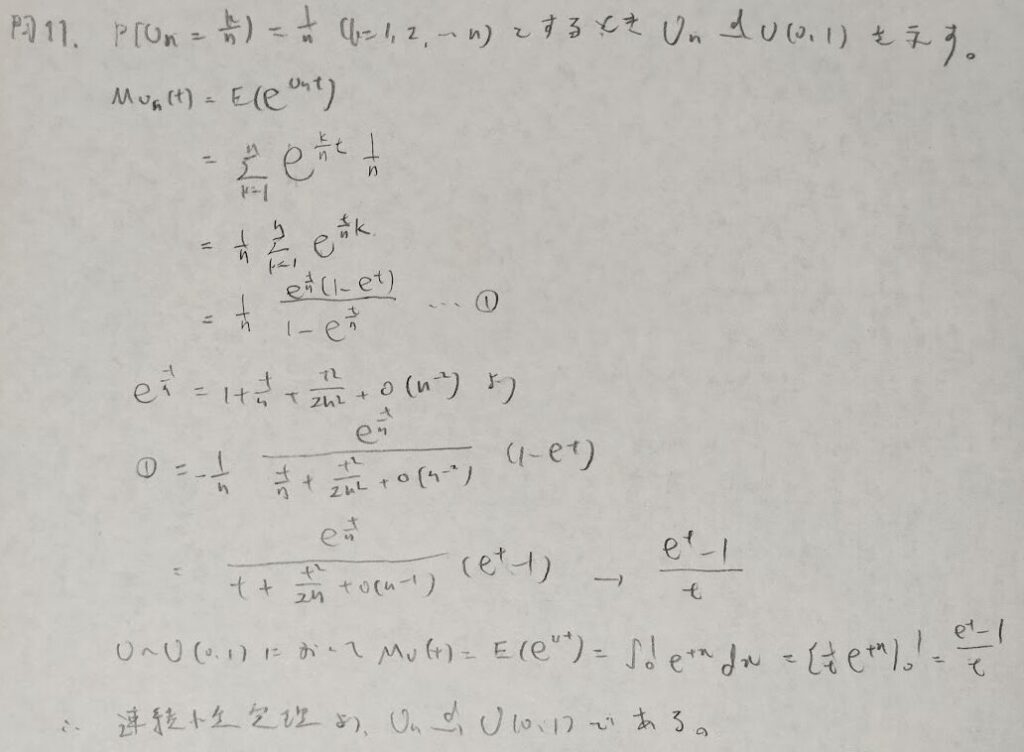
難問です。まず積率母関数の立式があまりみないタイプなので詰むポイントです。またテイラー展開を分母に適用する考え方も難しいです。指数関数系とロピタルの定理は相性が悪いです。素直にテイラー展開をお勧めします。
問12:ガンマ分布と漸近分布
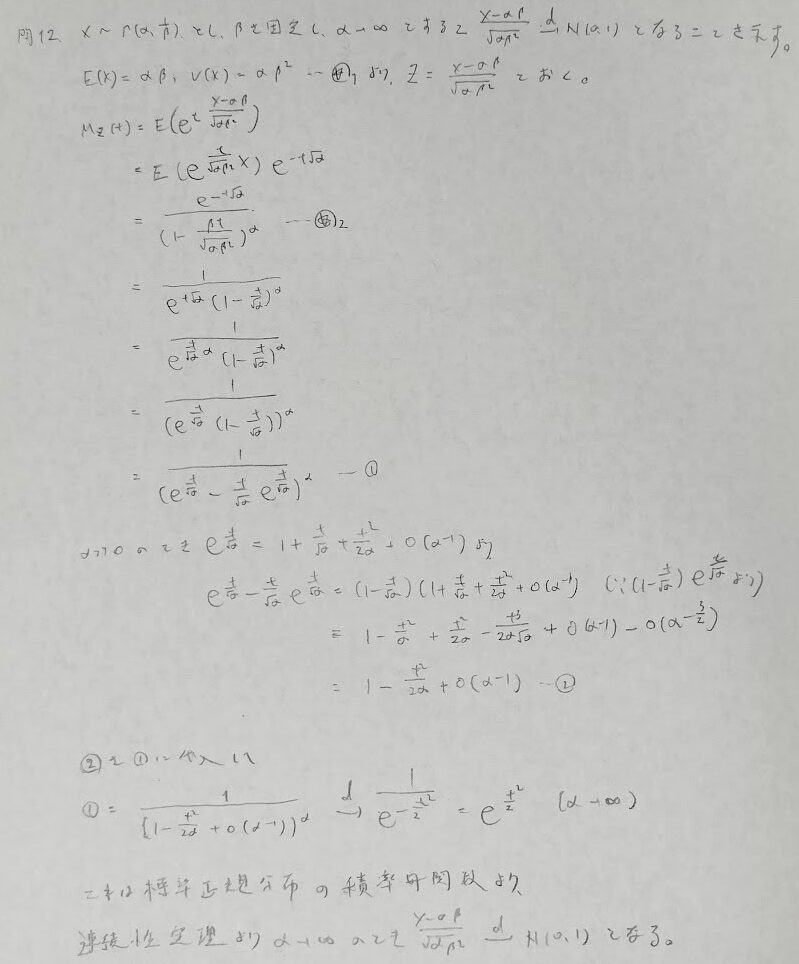
これぞ統計検定1級の1大問に匹敵するボリュームです。さまざまな基礎知識が要求される難問です。
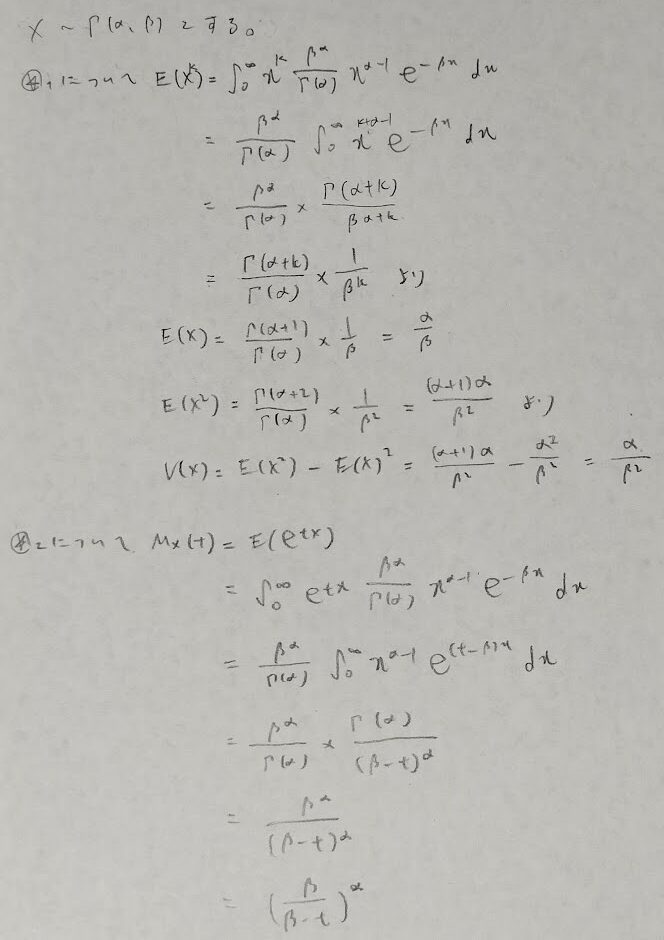
以上で第6章は終了です。前章と比べて理論の流れが綺麗で、この極限定理の賞のみでも『データ解析のための数理統計入門』で学ぶメリットを享受できます。解いていて気づいたのは、どの問題も統計検定1級の大問として選ばれても謙遜ない絶妙なレベル感であることです。ともに復習を頑張りましょう!









