統計検定１級の対策書として公式本以外で真っ先に買うべき本である『データ解析のための数理統計入門』の第７章の解説と演習問題を自力で解いた学習の軌跡の記事です。本章の位置付けは、確率分布編のまとめ的な章です。次の章から推定や検定になるため、ここで本書の第Ⅰ部が終了するイメージですね。
本章では積率母関数の考えをメインとした論理が展開されます。類書ではわかりにくかった内容も積率母関数を用いれば理解が明解になり感動を覚えるはずです。
統計検定１級青本の第７章の説明と例題
第７章は「カイ２乗分布、t分布、F分布→標本分布と不偏分散の独立性→t統計量関連の話題」の流れで論理が展開されます。相変わらず、わかりやすい構成になっており著者の久保川先生に感謝です。
初めにカイ２乗分布→t分布→F分布の順に定義→定理の解説をします。これらの標本分布は推定や検定で重要な役割を演じます。また準備段階としてガンマ分布やベータ分布は学習済みであることが望ましいです。
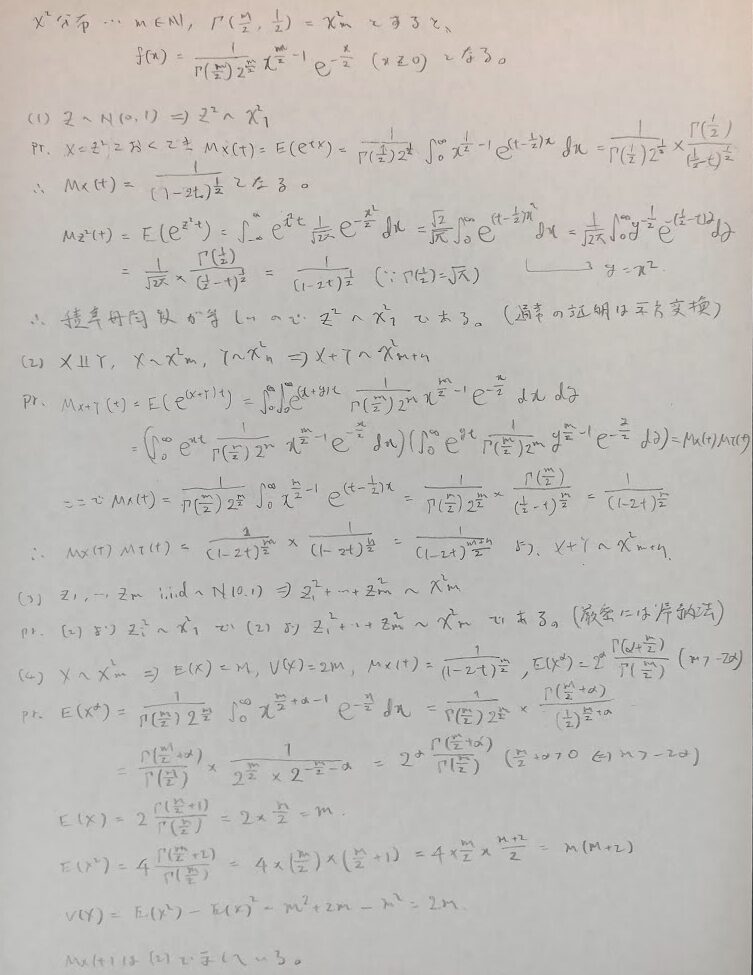
一応、t分布の分散も混合分布の考えを用いて時短で導いてみます。
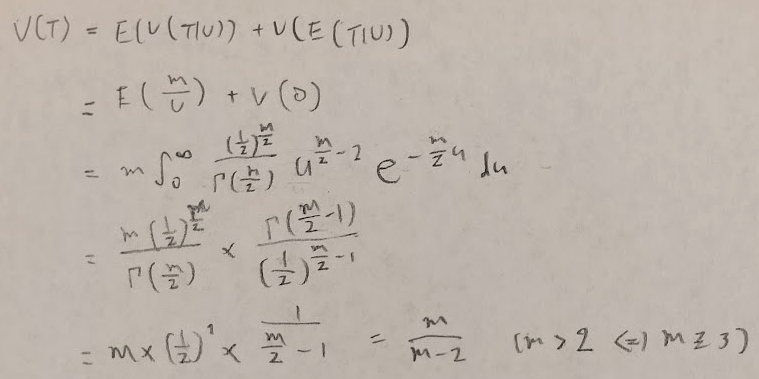
最後にF分布になります。最も計算が多い箇所となります。F分布の期待値とt分布の分散は等しくなります。
いよいよメイン部の標本平均と不偏分散の独立性に関する部分に入ります。多くの書籍ではヘルマート行列を用いた証明が主流ですが難易度が高く、個人的には理解はできるが試験で実際にヘルマート行列を構成できるか？と問われれば難しい気がします。『データ解析のための数理統計入門』では積率母関数を主軸に理論を展開しているため分かりやすく、実践もしやすいことに大変有用性を感じます。
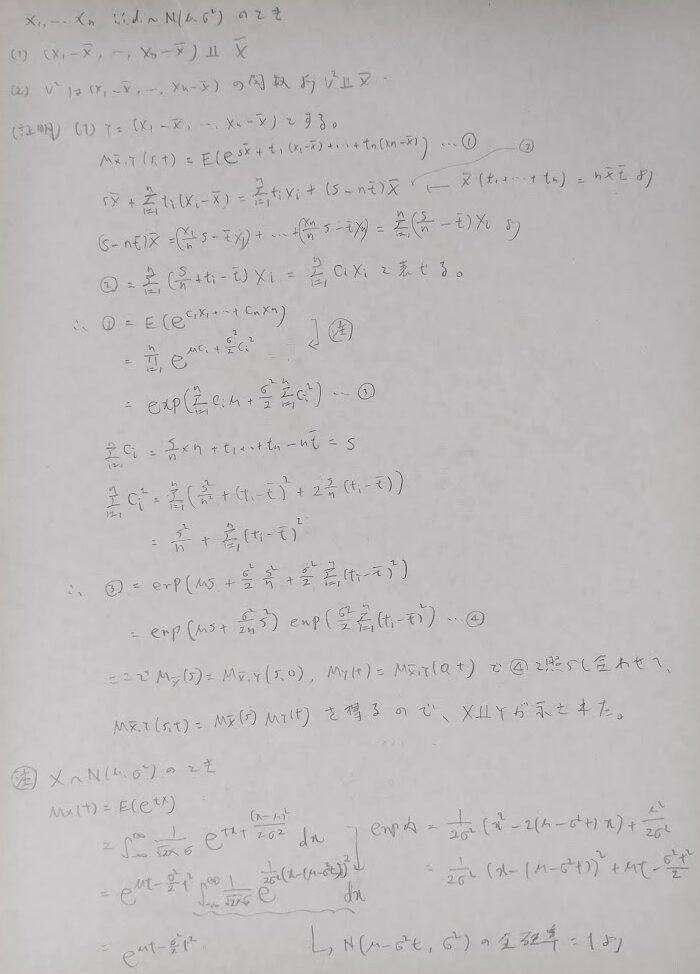
標本平均の従う分布はわかりますが、不偏分散が絡んだ分布が具体的にどのような分布に従うか知りたいところですね。
そこでt検定で用いることの多い標本分布が従う分布をもとめてみましょう。
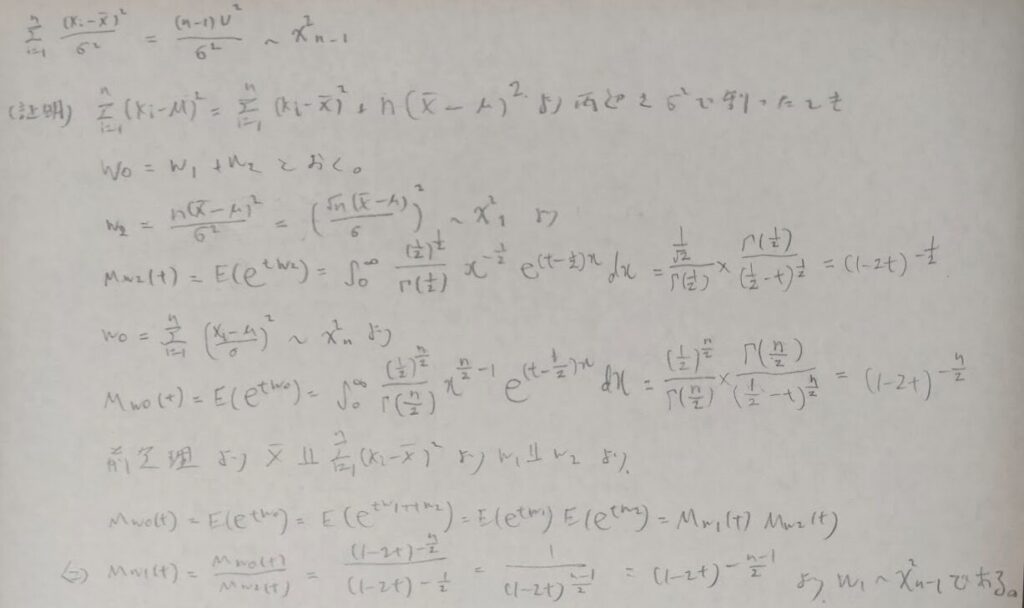
ようやく材料が揃ったのでt統計量を定義します。これによってスチューデントのトリック（母分散を不偏分散に代替すること）を用いることが可能になります。
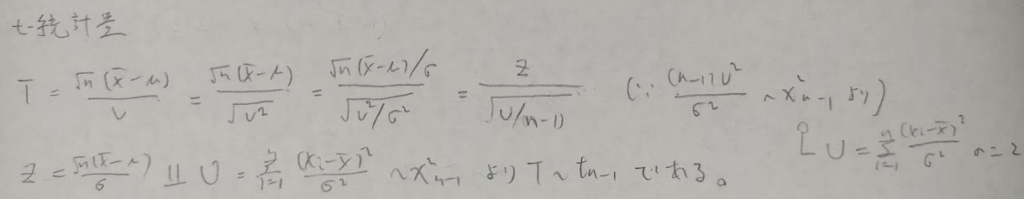
これでやっと推定や検定への道のりが開かれたわけです。推定は次回の章で学習していきます。
統計検定１級青本の第７章の演習問題の解説
問１：標準正規分布の利用
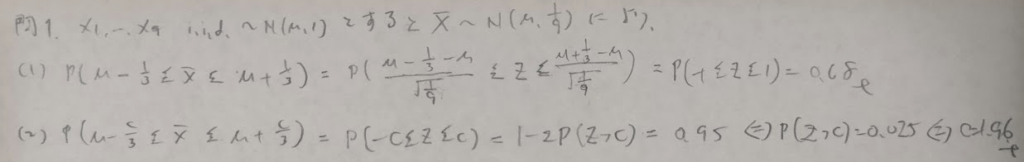
問２：t分布の利用
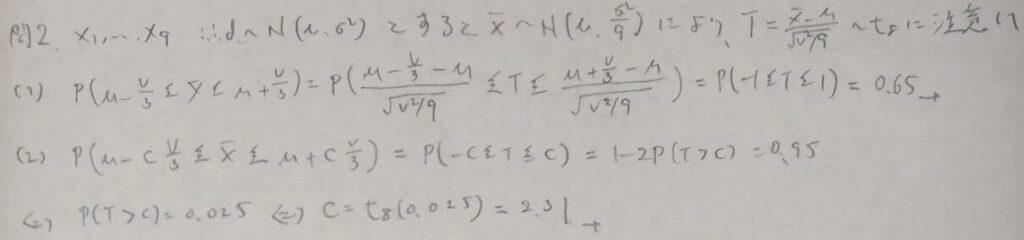
個人的にこの問題は素晴らしいと思います！僕はこのタイプの問題は初めて見ました。実際に試験で出た場合、ほとんどの方が無意識のうちに標準正規分布に帰着させてしまうと思います。そこの盲点をついた素晴らしい問題です。
問３：不偏分散の２乗の平均と分散
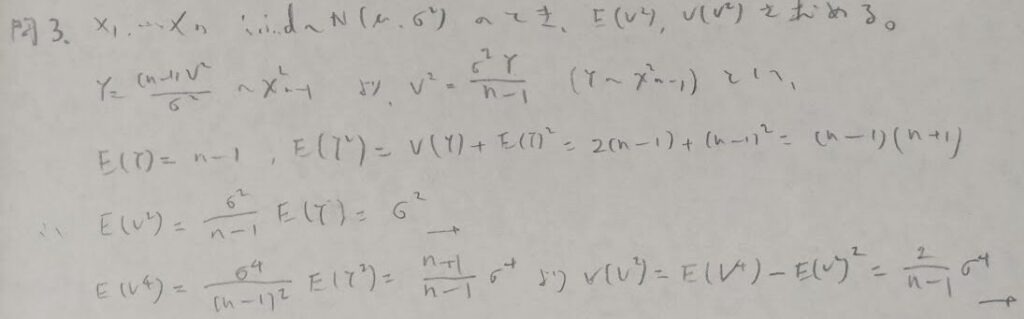
この問題は真正面から特攻すると処理量が大変になります。素直に既知の分布になるような置き換えを検討しましょう！
問４：変数変換
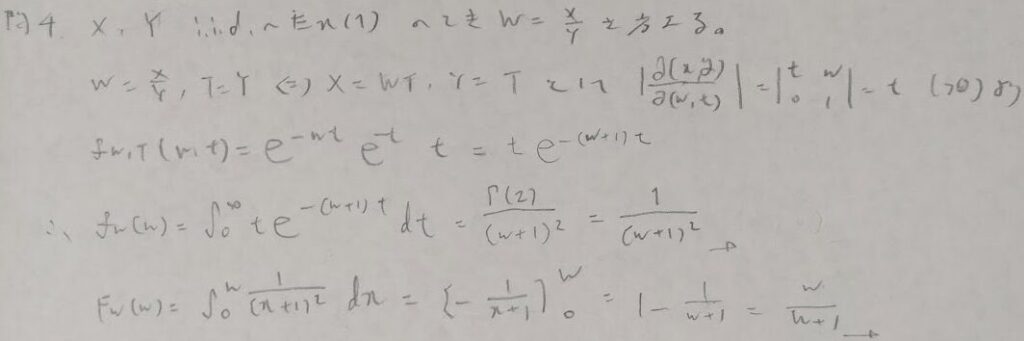
ここにきて突然の素直な問題でした。
問５：総合問題
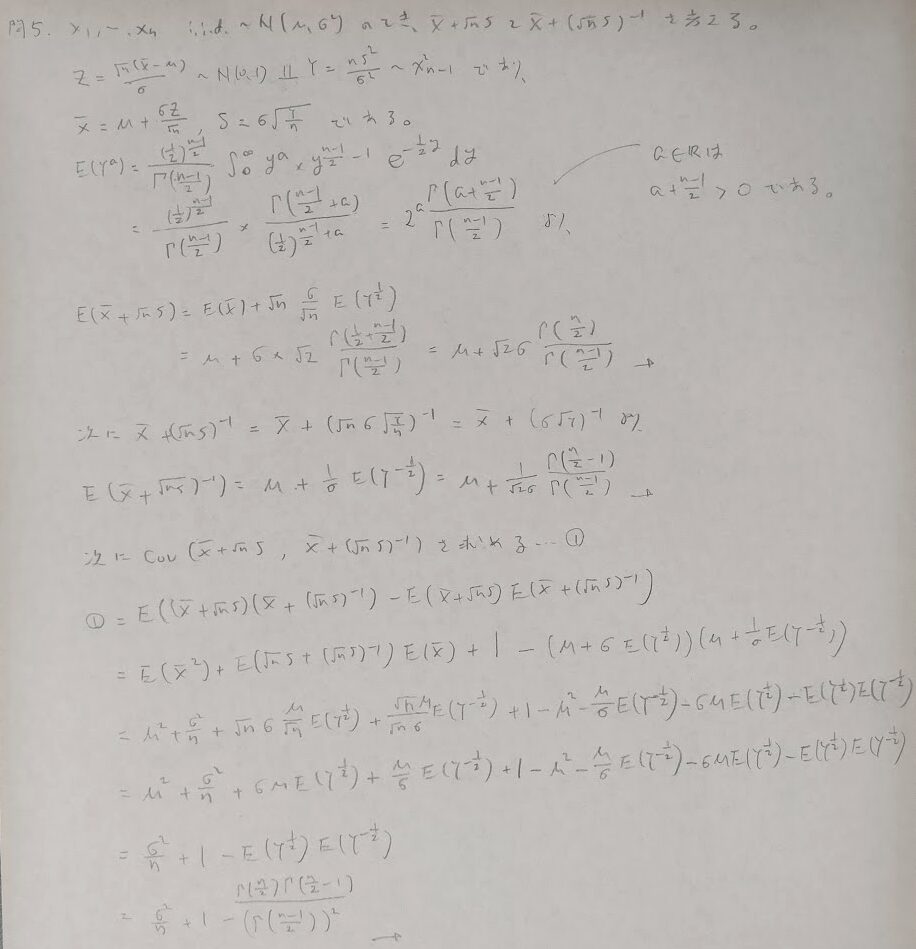
この章の内容のテーマをふんだんに取り入れた良問です。処理量が多いですが、しっかりと解ければ確かな実力がつきます。
問６：デルタ法
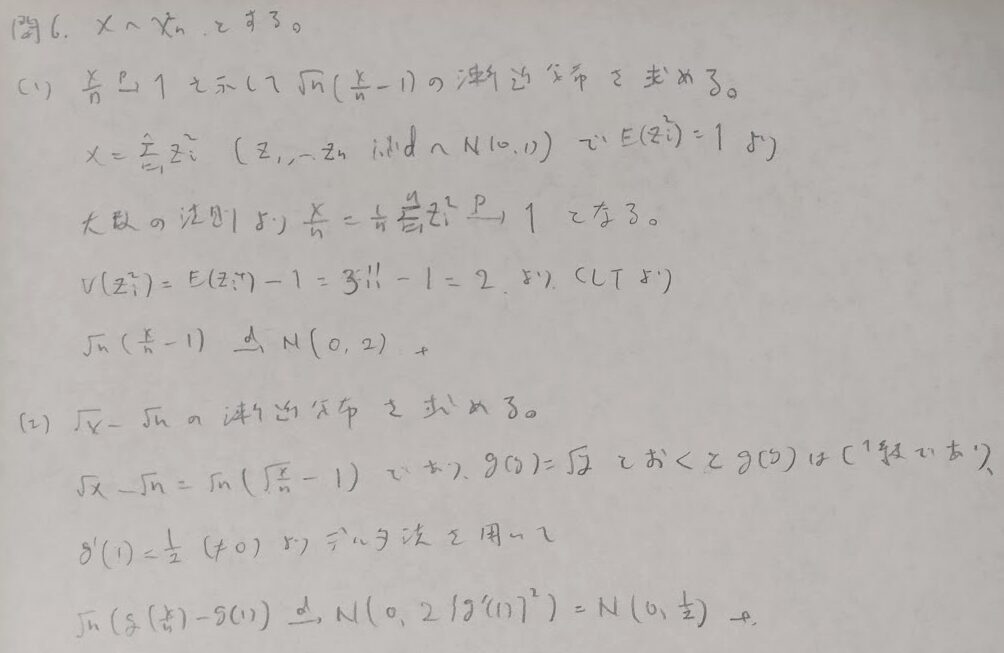
前章の内容の復習問題です。
問７：積率母関数の盲点（積の形）
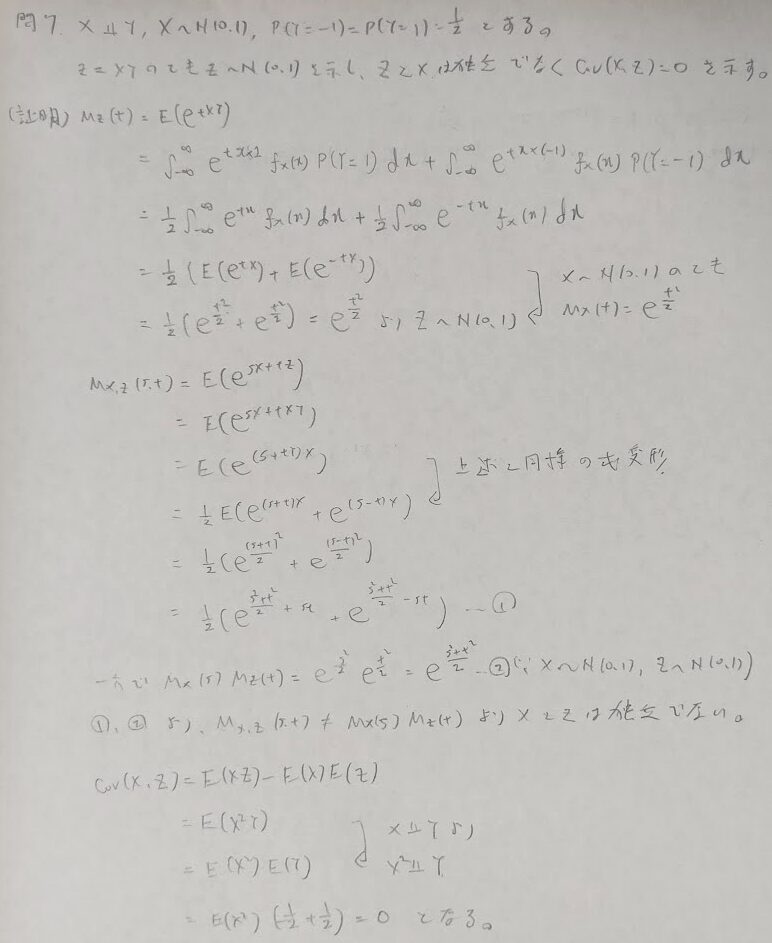
この問題は離散型と連続型のミックスタイプで、非常に混乱を招く問題です。しかし素晴らしい問題です。模範解答ではサラッと流されていた箇所の行間を自分なりに補って解きました。
問８：積率母関数と対称性
順序統計量の話題など、今までの章で学習してきた内容を活用する良問でした。総じてこの章の演習問題は確率分布編のまとめとしての役割を演じていました。次回からは推定や検定の内容になります。ともに頑張りましょう！
