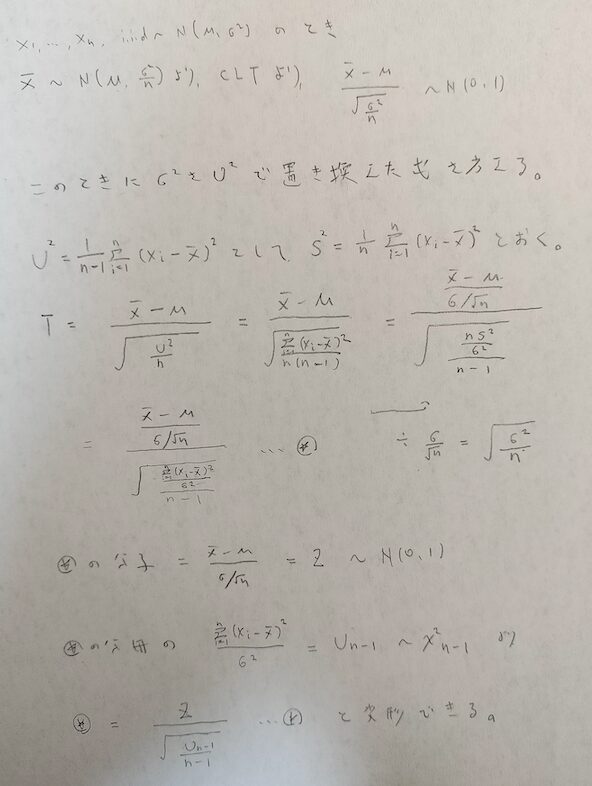統計学のメイン部分の区間推定について解説していきます。点推定では区間推定の信頼区間の作り方の方法をわかりやすく説明するため、最尤推定量と不偏推定量についても解説します。
まず信頼区間の作り方の概要を提示します。信頼係数はすべて1-εで統一します。
信頼係数1-εの信頼区間の作り方(『統計学大百科事典 仕事で使う公式・定理・ルール113』を参考)
1.母集団のパラメータを用いて標本の統計量の分布を作る(この統計量をどうするか?がかなり大事!)
2.確率1-εとなる統計量の範囲を求める
3.統計量の実現値が入るとして2.の範囲をパラメータについて解くと信頼係数1-εの信頼区間が得られる。
とても抽象的ですが、4つの例題を通してわかりやすく説明します。
統計量とはなんですか?
統計量とは標本から作られた関数です。ただし、その関数の中には未知のパラメータを含まないようにします。
うまく統計量を作り出すにはコツがあります。そのコツを教えていきます!
区間推定で用いる統計量の作り方
点推定の1つである最尤法を用いて、最尤推定量から出発するとうまくいくことが多いです。(『リスクを知るための確率・統計入門』から得た知識です。)
この記事では正規分布のパラメータ(母平均と母分散)の区間推定を行うので、正規分布のパラメータについての最尤法を用いて説明します。
最尤法の考え方とは「尤度を最大にするパラメータ(母数)を選ぶということは、(ここでは正規母集団の)モデルのうちで起きたことの確率を1番大きくするようなモデルを選ぶということ」という考えに基づきます。最尤推定量の標本にそれぞれの実現値を入れたものを最尤推定値といいます。
ここでは形式的に2つのパラメータが未知として尤度(関数)を立てて、対数尤度(関数)を求めてから尤度方程式を立式して最尤推定量を出しています。尤度や対数尤度の( )内の母数は未知母数のことです。図01では母平均も母分散も未知としています。そのため最後の母分散の最尤推定量では本来、母平均の最尤推定量を代入すべきですが、説明の流れ上、そのまま母平均を代入しています。

それでは母平均が既知の場合と未知の場合での母分散の最尤推定量を計算してみましょう。
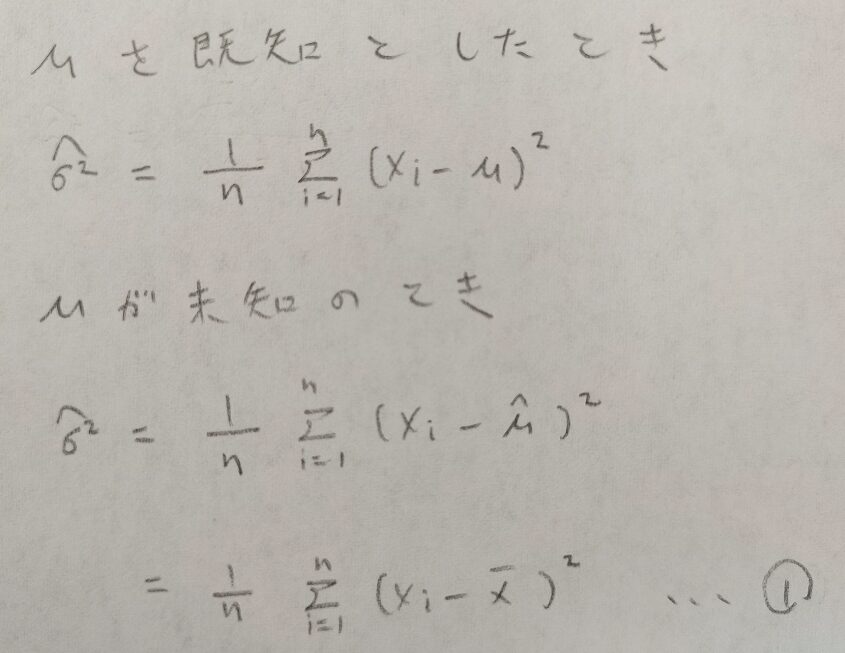
母平均の最尤推定量が標本平均でしたという結果は自然な流れだと感じました。そして母平均が未知の場合は母分散の最尤推定量として標本分散を用いるのも当然という感じがします。
ただし、標本分散は不偏性を満たさないので、母分散に関しては区間推定を行う際は最尤推定量ではなく、不偏推定量を用いることになります。
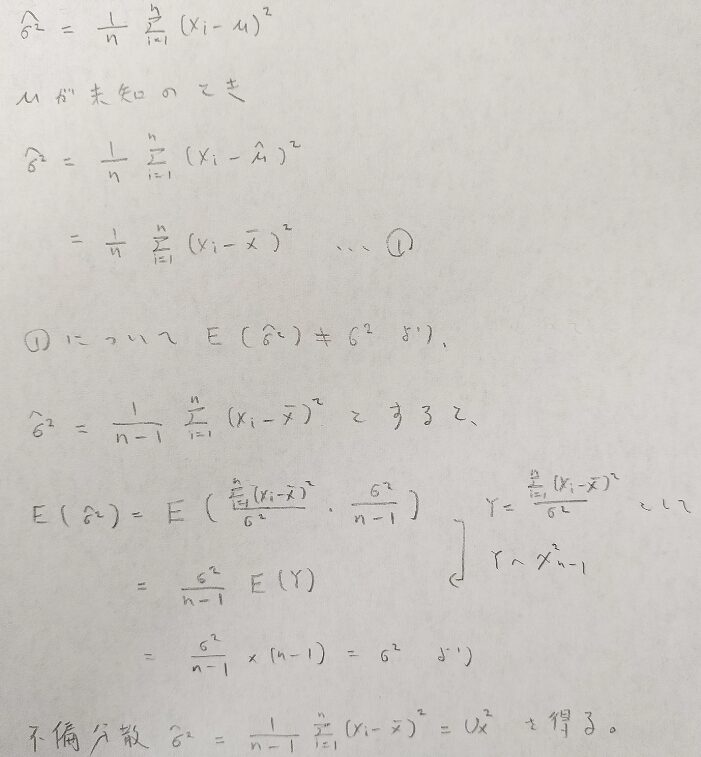
混乱を避けるために標本分散と不偏分散をまとめておきます。右辺は記号で、MLは最尤推定量の英語(maximum likelihood estimator)から、Uは不偏推定量の英語(unbiased estimator)の頭文字をとっています。MLEと母数の前につける流派もあります。
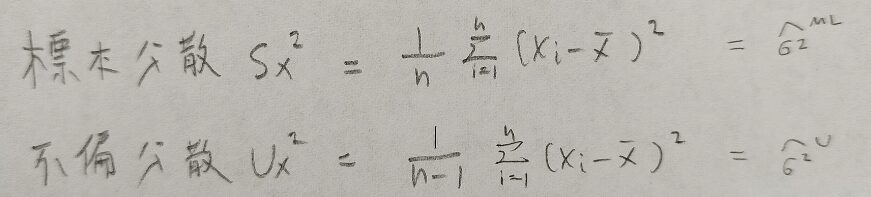
正規分布の母平均の区間推定(母分散既知)
信頼係数1-εの信頼区間の作り方(『統計学大百科事典 仕事で使う公式・定理・ルール113』を参考)
1.母集団のパラメータを用いて標本の統計量の分布を作る(この統計量をどうするか?がかなり大事!)
2.確率1-εとなる統計量の範囲を求める
3.統計量の実現値が入るとして2.の範囲をパラメータについて解くと信頼係数1-εの信頼区間が得られる。
いよいよ区間推定を開始します。記事の冒頭で紹介した内容を具体例とともに説明していきます。
1.母集団のパラメータを用いて標本の統計量の分布を作る(この統計量をどうするか?がかなり大事!)
→母平均の最尤推定量である標本平均からスタートします。
→標本平均の従う分布を求めます。
→今回はそれをそのまま正規化するとN(0,1)に従う統計量Tの完成です。
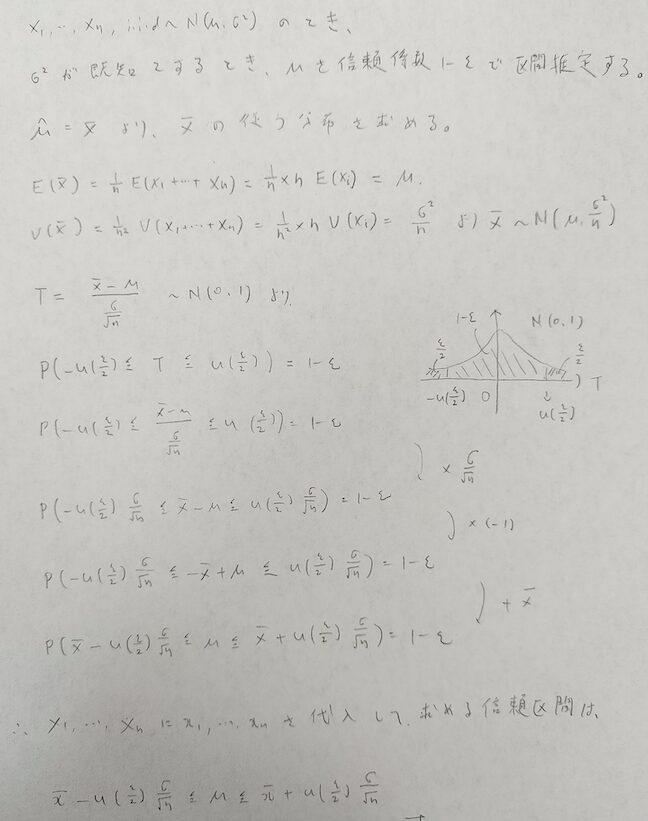
2.確率1-εとなる統計量の範囲を求める
→図05のグラフから標準正規分布は偶関数なことに注意して統計量の範囲を求める
3.統計量の実現値が入るとして2.の範囲をパラメータについて解くと信頼係数1-εの信頼区間が得られる。
→あとはP( )の( )を母平均μについて解けば良い。
正規分布の母平均の区間推定(母分散未知)
信頼係数1-εの信頼区間の作り方(『統計学大百科事典 仕事で使う公式・定理・ルール113』を参考)
1.母集団のパラメータを用いて標本の統計量の分布を作る(この統計量をどうするか?がかなり大事!)
2.確率1-εとなる統計量の範囲を求める
3.統計量の実現値が入るとして2.の範囲をパラメータについて解くと信頼係数1-εの信頼区間が得られる。
1.母集団のパラメータを用いて標本の統計量の分布を作る(この統計量をどうするか?がかなり大事!)
→今回は母平均の最尤推定量から出発しますが、母分散が未知なので変わりに不偏分散を用いますので正規分布の代わりにt分布が出てきます。この不偏分散は母分散の最尤推定量ではなく、分母がnからn-1に変わった量であることに注目してください。
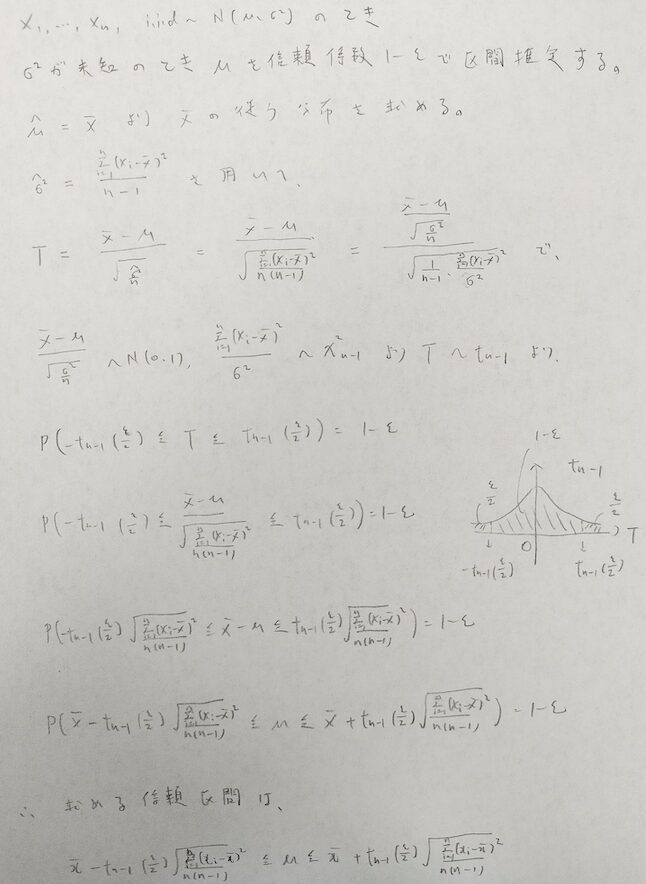
2.確率1-εとなる統計量の範囲を求める
→t分布も偶関数なので正規分布のときと同じように考えればOKです!
3.統計量の実現値が入るとして2.の範囲をパラメータについて解くと信頼係数1-εの信頼区間が得られる。
→母平均について( )内を解きます。落ち着いて処理しましょう!
正規分布の母分散の区間推定(母平均既知)
一般的な書籍だと母平均と母分散の区間推定は別々の箇所で説明されます。しかし本記事では「正規母集団という観点を第一としているため」つまり正規分布のパラメータの区間推定というテーマのため、一度に扱います。
信頼係数1-εの信頼区間の作り方(『統計学大百科事典 仕事で使う公式・定理・ルール113』を参考)
1.母集団のパラメータを用いて標本の統計量の分布を作る(この統計量をどうするか?がかなり大事!)
2.確率1-εとなる統計量の範囲を求める
3.統計量の実現値が入るとして2.の範囲をパラメータについて解くと信頼係数1-εの信頼区間が得られる。
1.母集団のパラメータを用いて標本の統計量の分布を作る(この統計量をどうするか?がかなり大事!)
→母平均の最尤推定量からスタートします。
→分子がカイ2乗分布にかなり近い形をしているので図07のように式変形をしてカイ2乗分布を作り出します!
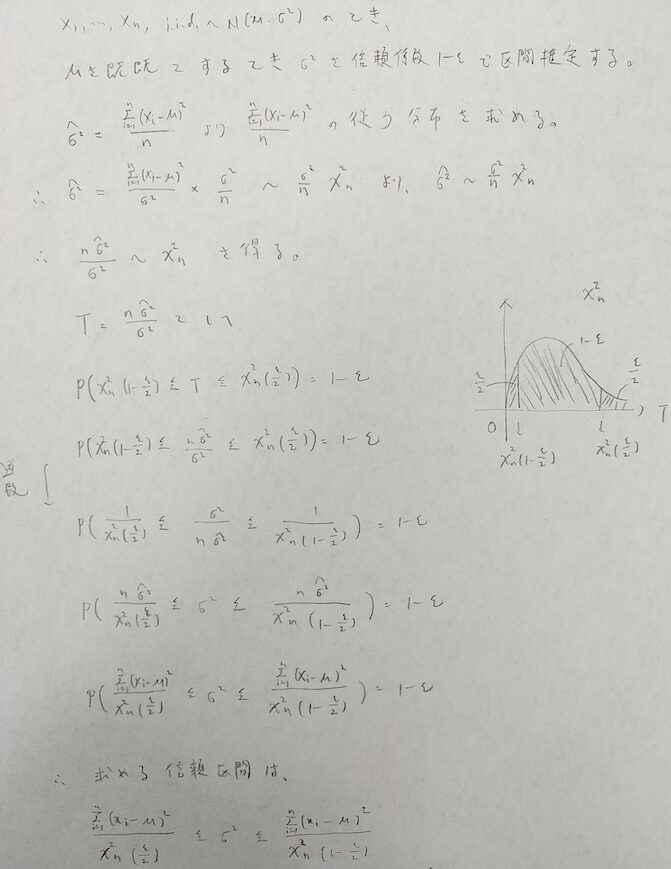
2.確率1-εとなる統計量の範囲を求める
→カイ2乗分布は偶関数ではないのでないので注意!
3.統計量の実現値が入るとして2.の範囲をパラメータについて解くと信頼係数1-εの信頼区間が得られる。
→これらは母平均の区間推定のときと同じように処理します。
正規分布の母分散の区間推定(母平均未知)
いよいよ最後ですね!
4番目の例題として、ここでは(下の図08を隠して)何も見ずに母分散の区間推定をやってみて下さい!
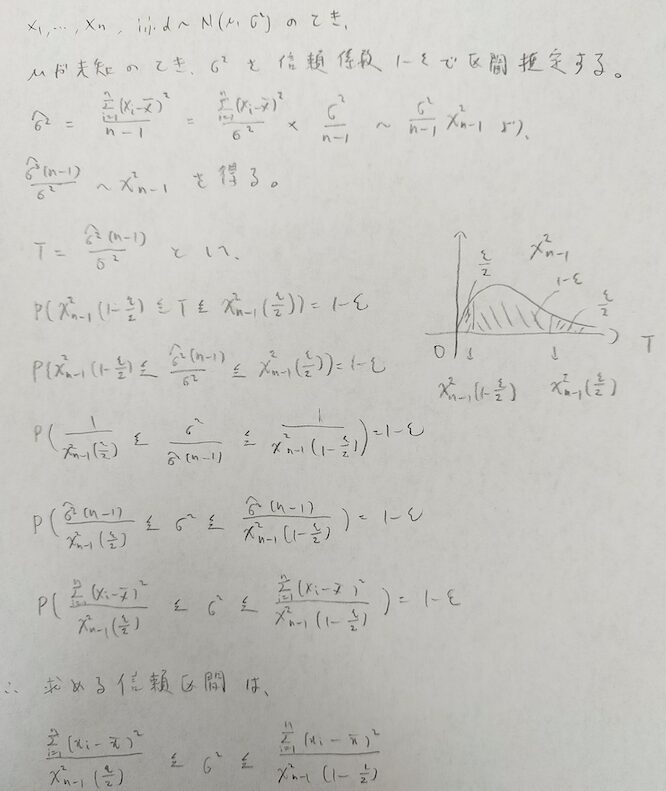
これは自由度n-1のカイ2乗分布が出てくれば流れ作業的に結論までいけますね!
区間推定で大切なのは統計量の作り方です。最後にもう1度、信頼区間の求め方を載せておきますね。
信頼係数1-εの信頼区間の作り方(『統計学大百科事典 仕事で使う公式・定理・ルール113』を参考)
1.母集団のパラメータを用いて標本の統計量の分布を作る(この統計量をどうするか?がかなり大事!)
2.確率1-εとなる統計量の範囲を求める
3.統計量の実現値が入るとして2.の範囲をパラメータについて解くと信頼係数1-εの信頼区間が得られる。
そういえば信頼区間の意味については勘違いして理解していませんか?
①の意味ではなかったのですね!!区間推定の信頼区間の意味について間違った理解をしていました!危ないところでした。
正規分布のパラメータの区間推定のまとめ
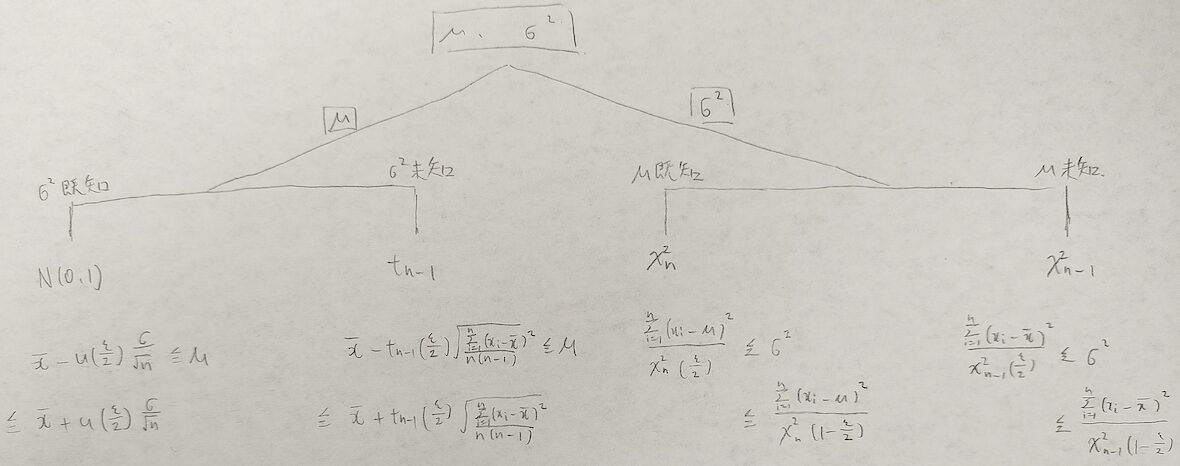
この記事の最後に正規母集団の母数の区間推定を4つをまとめておきます。
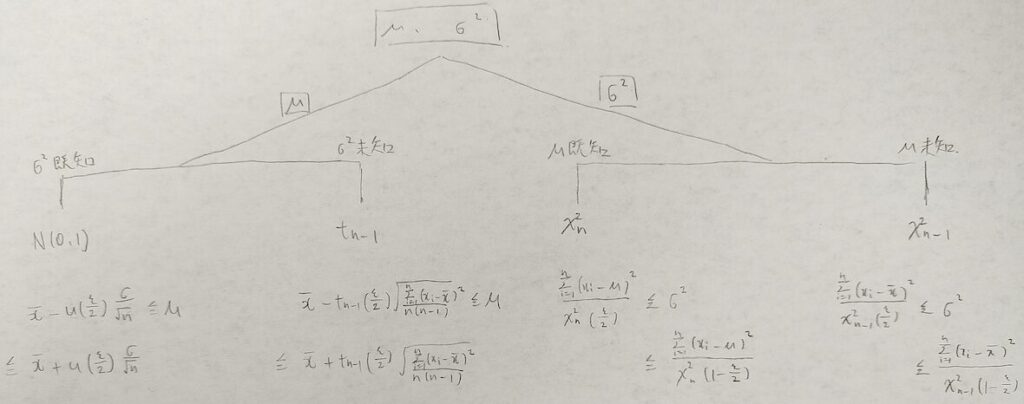
次の2つの大前提を確認してから図09のフローチャートへと進んでください。
母平均が未知なら標本平均(根拠は最尤推定量)を使います。
母分散の区間推定にはカイ2乗分布が出てきます。
最尤推定量の意味ついてこの本の説明がしっくりきましたのでご紹介します。