統計検定1級よりも試験としての難易度が高いアクチュアリー数学が指定する確率分野の演習書である『確率統計演習 1 確率』の対策を全6回に分けて解説します。具体的には本書に掲載されている例題と問題の解説を行います。掲載されている問題の詳しい設定などは本書の内容をご覧ください。
2023年の12月にアクチュアリー数学を受けたのですが『確率統計演習 1 確率』までしっかりと手が回らなくて不合格となってしました。2024年の試験では本書をしっかりと攻略してから挑みたいと思います。
過去問を結構頑張っていましたよね。最近は初見問題が増えているので過去問だけの演習だと「ケアレスミス」があったときに致命的になりますのでご注意くださいね!
今回の国沢確率に関する記事は下記のように7記事に分けて解説を行っていきます。本記事はその第1回に当たる内容です。
第1章:事象と確率
第2章:確率変数と分布
第3章:平均値、分散
第4章:変数変換と和の分布
第5章:積率と積率母関数
第6章:大数の法則と中心極限定理
実際は第7章「大数の強法則」もあるのですがアクチュアリーのホームページの試験範囲には試験範囲という記載がないため、試験対策として除外しています。
アクチュアリー数学は統計検定1級とは異なり、試験範囲が明確に決まっているので対策の際には余分な箇所まで学習しないような注意が必要です。ただでさえ暗記量が多い試験なので効率的に試験対策は行いたいですね。
『国沢確率』第1章「事象と確率」の例題

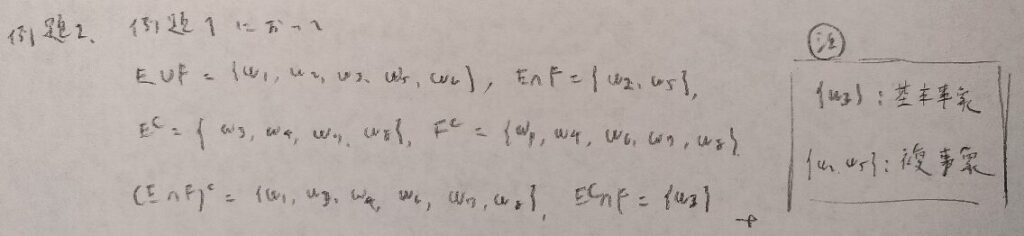
上の注のように事象には基本事象と複事象の2つがあります。
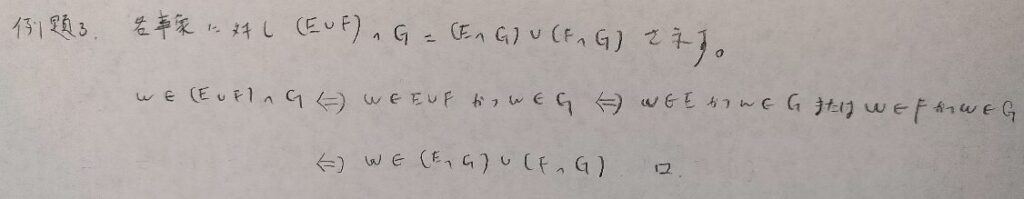
和集合の記号を+記号として、積事象(共通部分)の記号を×とすると、分配法則のような関係が成り立っています。
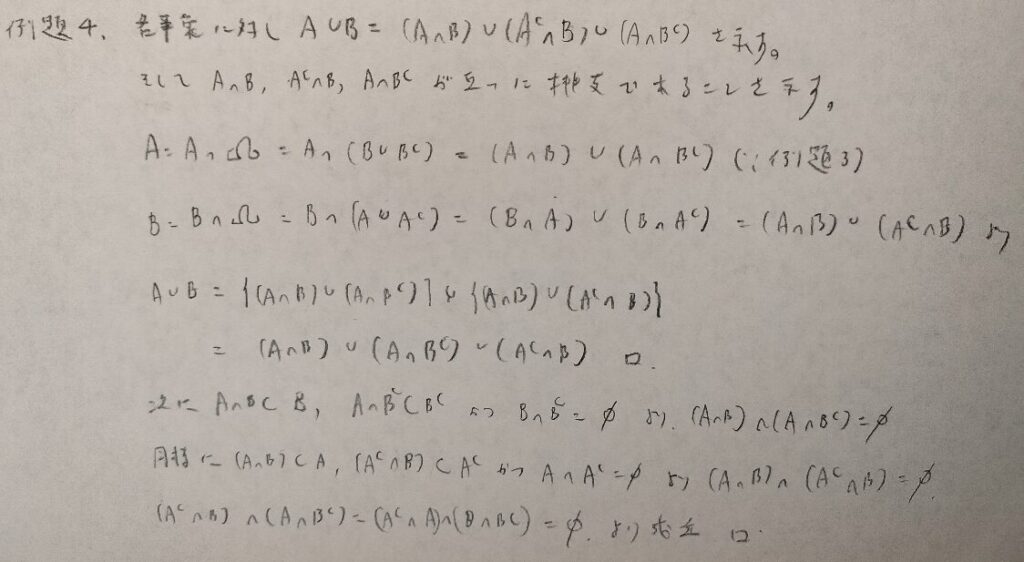
最後の方がテクニカルで初見では難しいです。
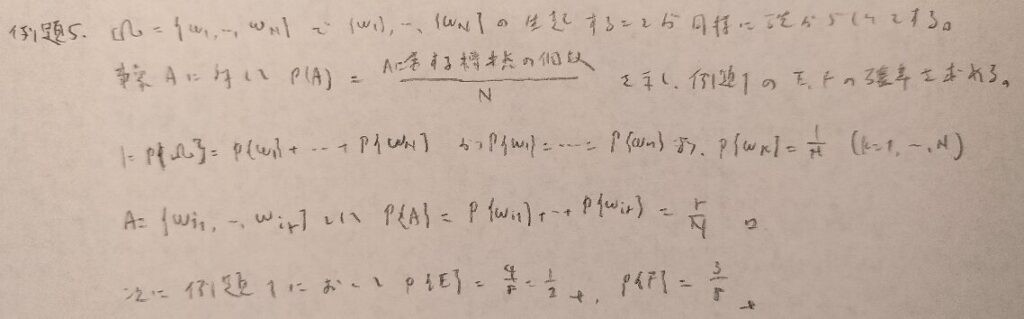
当たり前に感じることをきちんと証明する問題ですね。
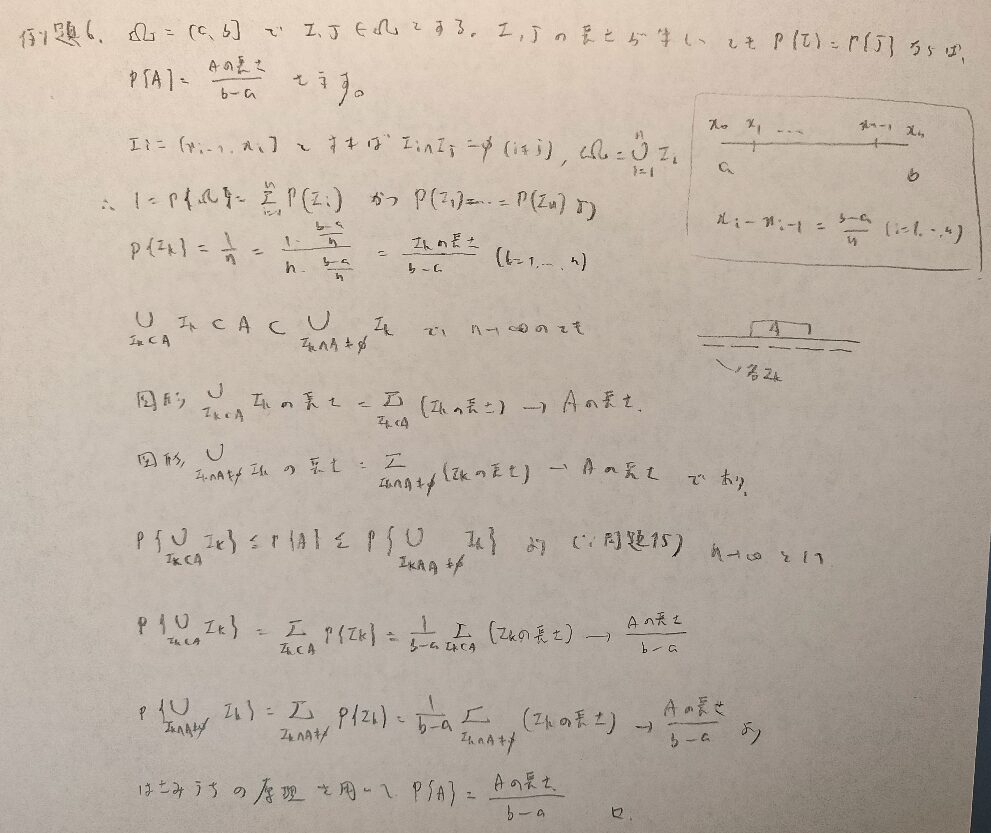
難問です。のちに2次元に拡張されます。これ系の問題は本書『確率統計演習 1 確率』にのみ掲載されています。
どちらかというと統計検定1級に出てきそうな問題です。(傾向とずれている気がしますけどね!)


確率事象とは事象の中で、全体回数分の起こった回数が一定値に収束するような事象です。
加比の理は大学受験数学の中でも気づきにくさではナンバー1とも言われる内容です。証明は中1の文字式で登場するのですが、ここで出てくるとは…数学って面白いですね。
条件付き確率の箇所でまた再登場しますのでお楽しみに!
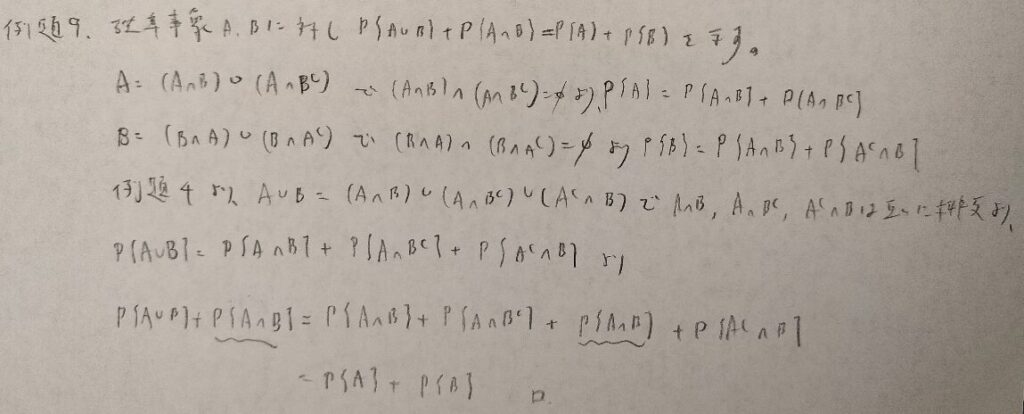
今後の問題では排反事象を意識しないと減点になる問題が増えます。
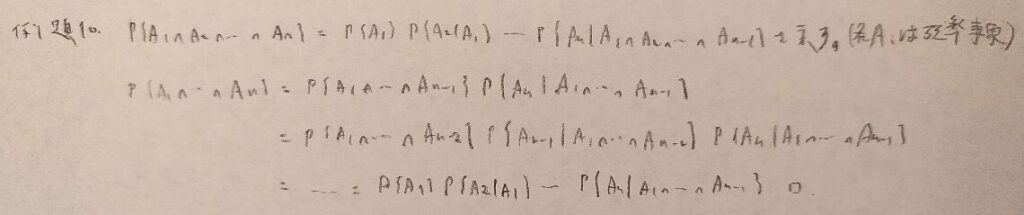
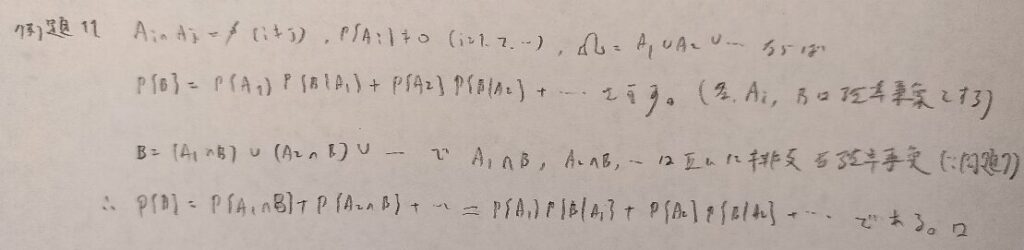
例題は以上になります。詳しい問題設定は『確率統計演習 1 確率』をご覧くださいね!
『国沢確率』第1章「事象と確率」の問題
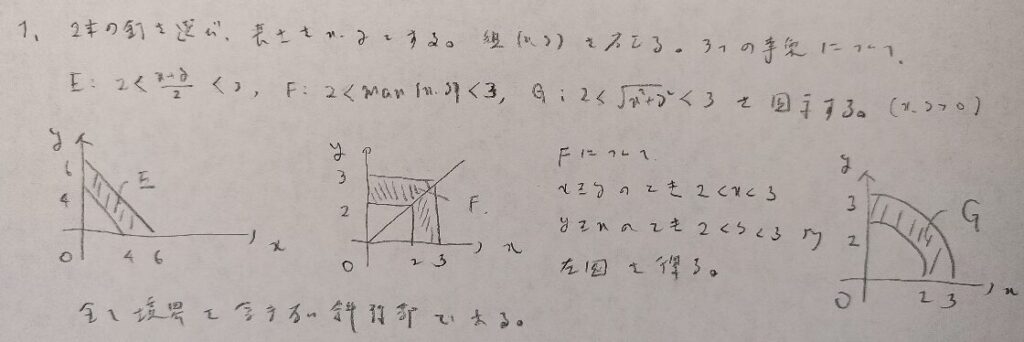
真ん中のFの問題は他書では見られない問題です。



本問は同様に確からしくない場合にどのように対処するか?が分かりやすく解説されている良問です。アクチュアリー数学では未出です。
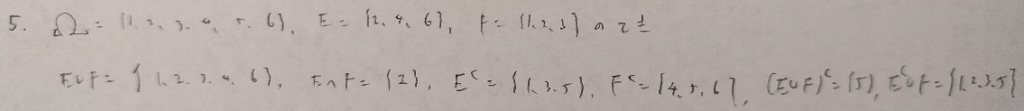
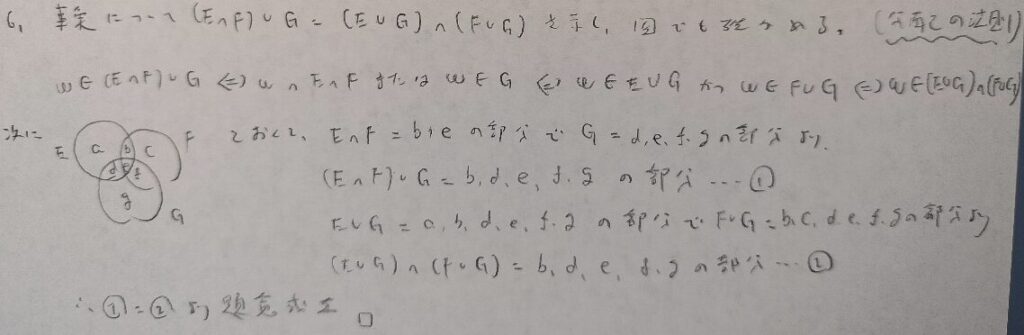
この問題、何回か解かないと身につかないパターンですよね。
実戦ではベン図で考えた方が早いですね。

排反の証明には背理法が有効です。
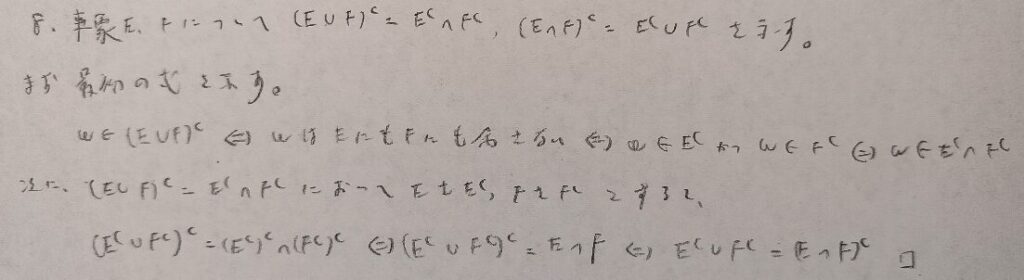
実は後半の証明は高校の教科書には載っていませんが、知っていると後半部は一瞬で証明できますね。
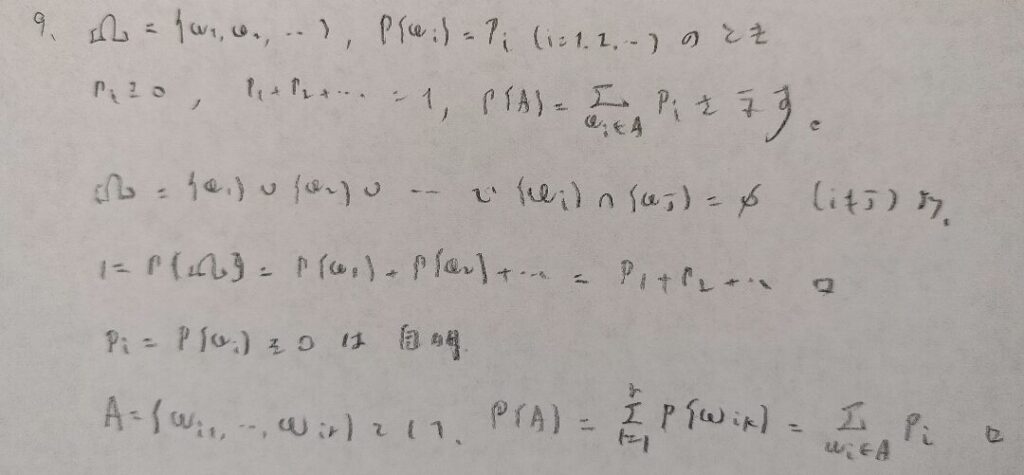

これがさっきの問題の2次元版ですね!
その通りです。この証明法3次元以上にも拡張できそうで汎用性がありますね。

どの参考書や問題集にも載っている超有名問題です。寝ぼけている状態でも答えを出せるようにしておきたい問題です。
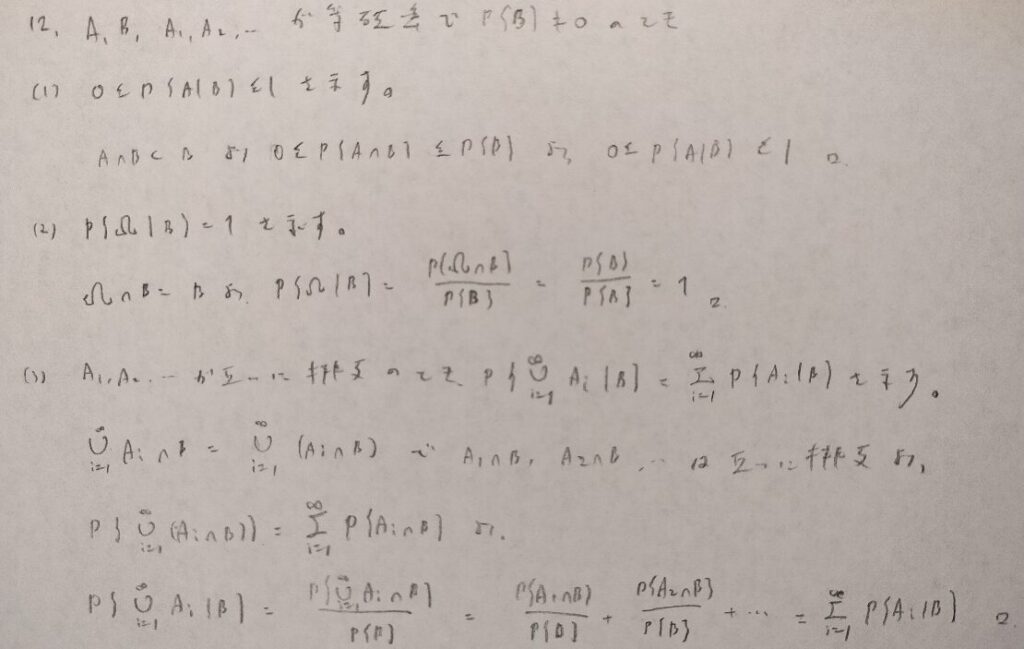
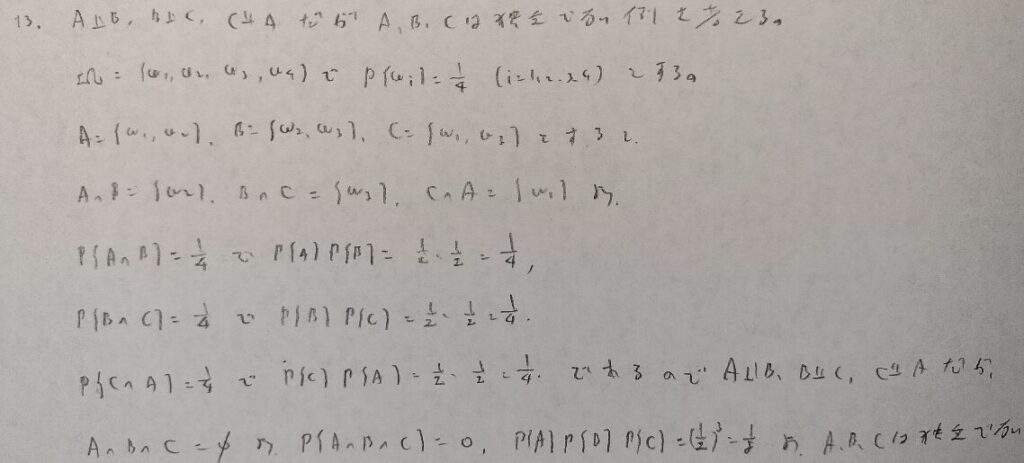
これ系の問題も色々な本に載っていますが、僕的には『確率統計演習 1 確率』に載っているこの例が最も再現性が高くシンプルで応用が効きやすいと感じました。
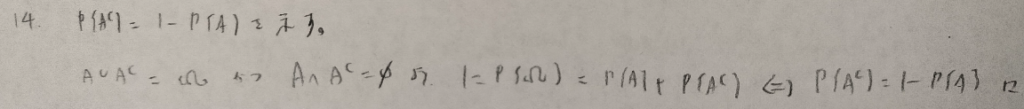
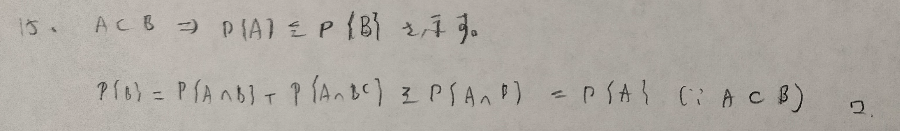
初見では難問です。2行目の最初の等式がややテクニカルです。

ボンフェロニーの不等式(の系)を示す問題で個人的に第1章の最難問です。直球で証明を与えているのが特徴的です。他書では変化球的な証明が目立つ問題です。
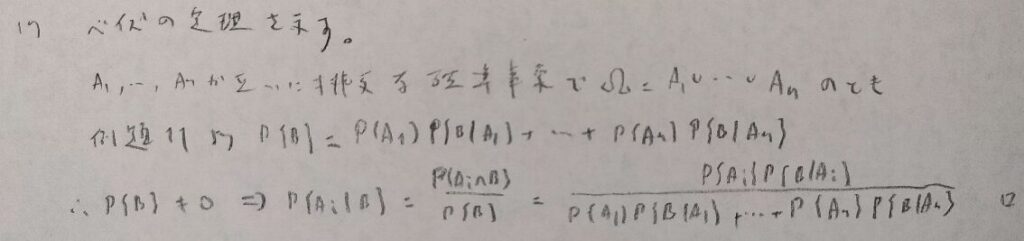

この問題がくじ引きの公平性の証明に用いられます。

第1章で最も現実的な問題を証明させる問題です。
長年疑問に思っていた問題が解決して満足です笑
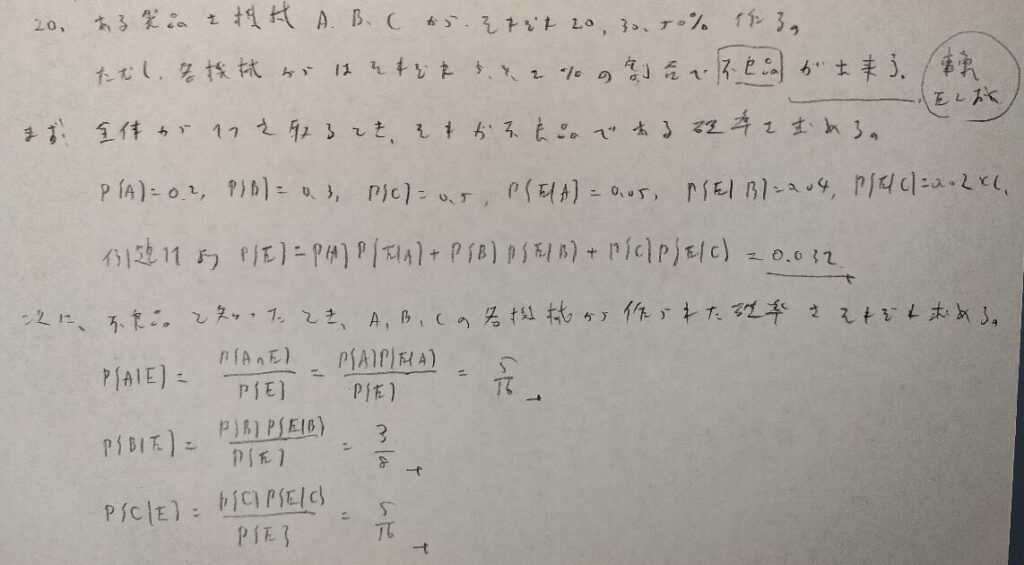
なんと最後は統計検定2級レベルの問題でフィニッシュです。このように『確率統計演習 1 確率』はバラエティーに富んだ面白い問題も散見されます。第2章以降も一緒に頑張りましょう!


