統計検定1級の対策書として公式本以外で真っ先に買うべき本である『データ解析のための数理統計入門』の第5章の解説と演習問題を自力で解いた学習の軌跡の記事です。条件付き分布の理解がメインになるので(自分含めて)苦手意識のある方は必見です!
本章は順序統計量→十分統計量→混合分布と進みます。それぞれの内容が程よくまとまっており、『データ解析のための数理統計入門』の質の高さを再確認した章になりました。
統計検定1級青本の第5章の説明と例題
順序統計量
n個の標本に対するnを標本のサイズといいます。無作為抽出はn個の確率変数が互いに独立と同値です。
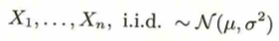
非復元抽出の場合はiidではありません。また上の定義は次のように書かれることがあります。
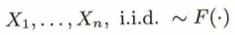
F(・)の関数系がわかっている場合はパラメトリック、そうでない場合はノンパラメトリックといいます。確率変数の組と確率分布との関係を記述したものを統計モデルといいます。統計モデルをどのように設定するか?を統計的モデリングといいます。想定した統計モデルは仮設検定や選択規準などを通して検討します。
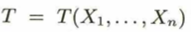
統計量の分布を標本分布といいます。パラメータ(母数)は標本から推測します。この関数を次のように考えて、θの推定量といいます。
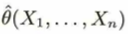
この取り方の1つに不偏推定量があります。これはすべてのθに対してθ^の期待値がθになることです。標本平均、標本分散、不偏分散を考える際はiidで考えます。
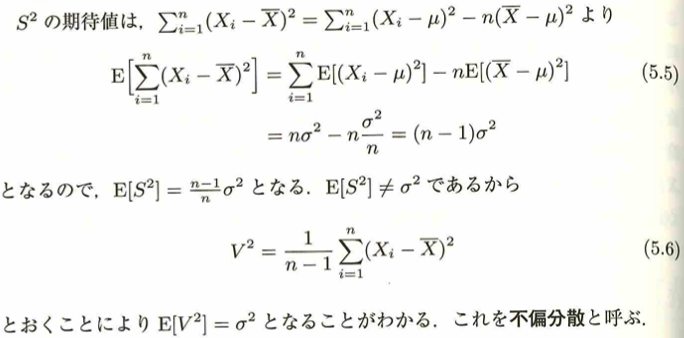
また統計量の1つとして順序統計量があります。これは事象と確率を対応させた多項分布の考えを用いた導出がわかりやすいです。
事象と確率の置き方と、確率密度関数への持っていき方をマスターすればいつでも復元可能です。
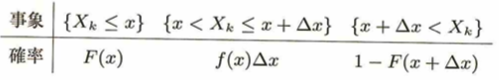
次の作業に行く際に、添字kを(j)つまり順序を導入することにより。事象を満たす際の個数が得られるので多項分布の考え方を適用できるようになります。
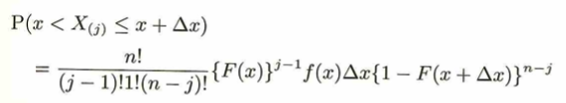
この次の極限の式でΔxで割っている意味はf(・)Δxは微小長方形の面積を表しているためです。
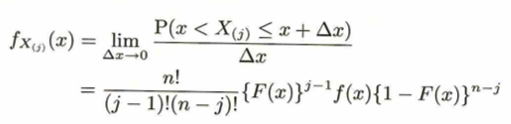
ただし公式を素早く導出したい場合は、Δ記号は省略して一気に求めておきたいですね。次の公式は同時分布になります。
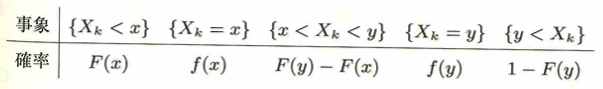
連続型確率変数の場合、f(x)=0となってしまうため形式的な表現になります。
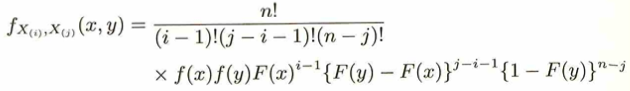
この特例が次の公式です。
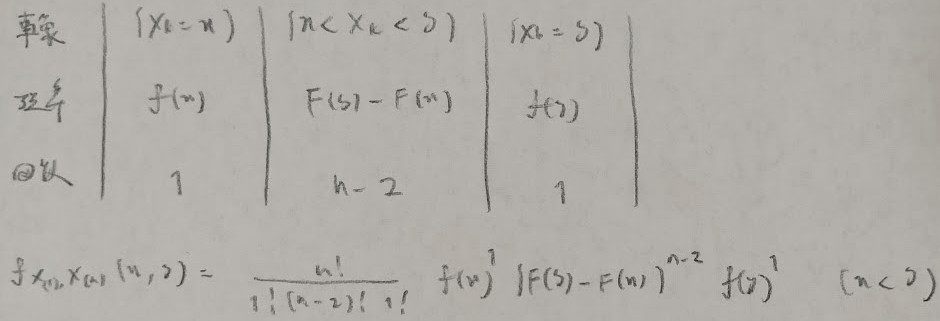
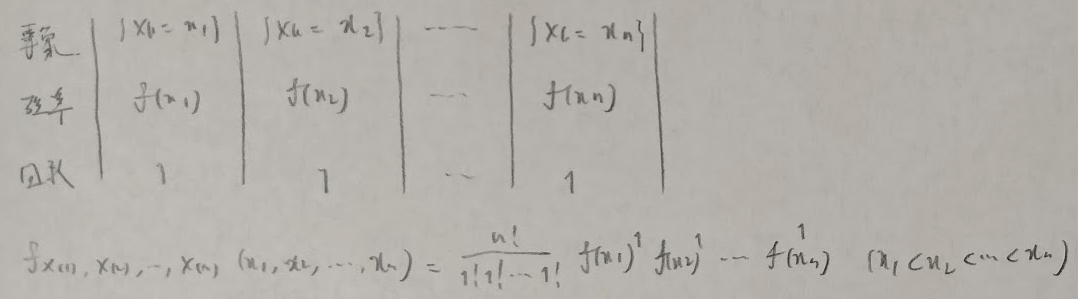
ここで有名な問題を紹介します。この問題の結果をアクチュアリー数学ではどんどん使っていくことになります。逆にこの結果を知らないと時間切れになります。
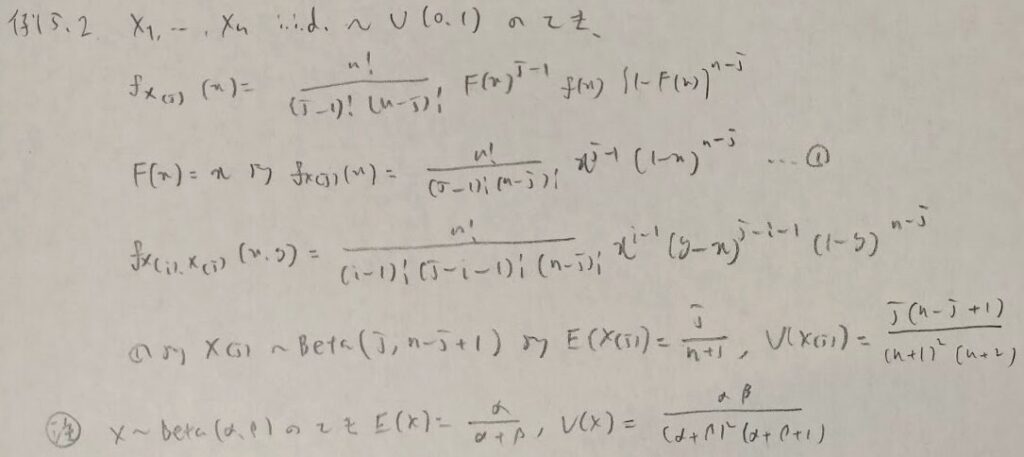
十分統計量
十分統計量は統計検定1級で頻出です。因子分解定理と合わせて有名な確率分布の問題はスーッと書けるようにしておきたいですね。

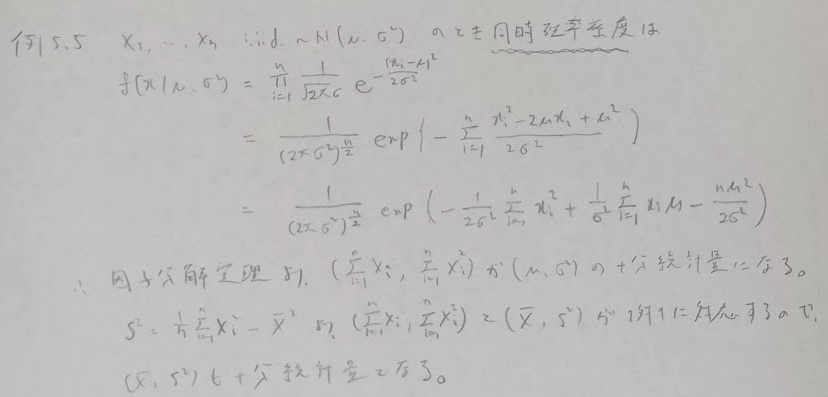
一様分布については統計検定1級でよく出題されます。
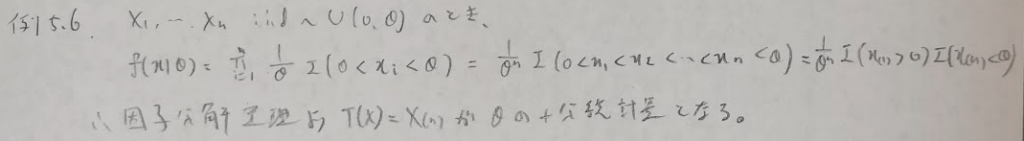
混合分布
次は抽象的になり難易度が上がる混合分布についてです。アクチュアリー数学では特に頻出です。
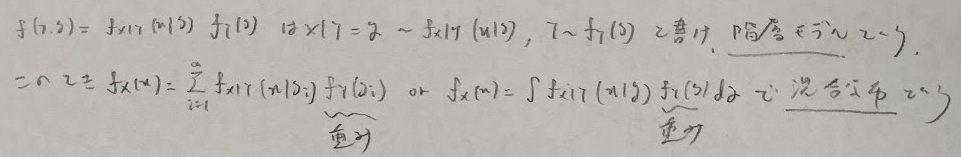
混合分布では確率(密度)関数まで求めさせる問題と期待値や分散のみでOKな問題に分かれます。期待値や分散では、繰り返し期待値や全分散の公式が大事になってきます。
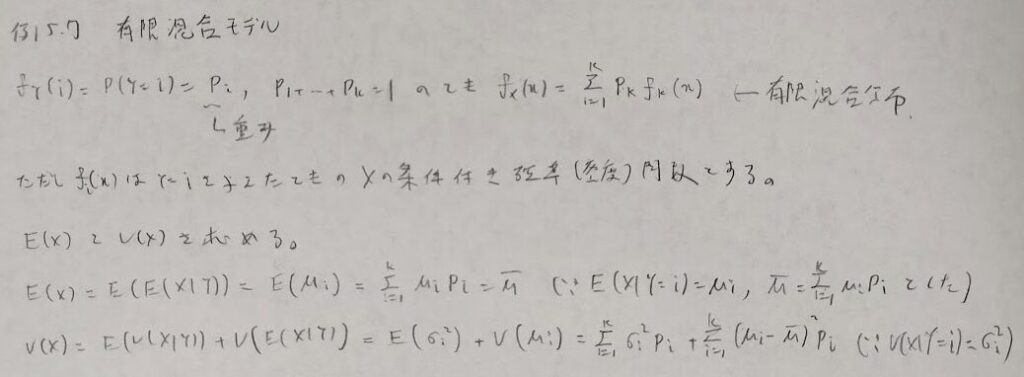
これは2つの正規分布を合わせたものとしてもよく出てくる形になります。次はt分布との関連です。実際は平行移動の概念を用いていますが、大きく考えてt分布というわけです。
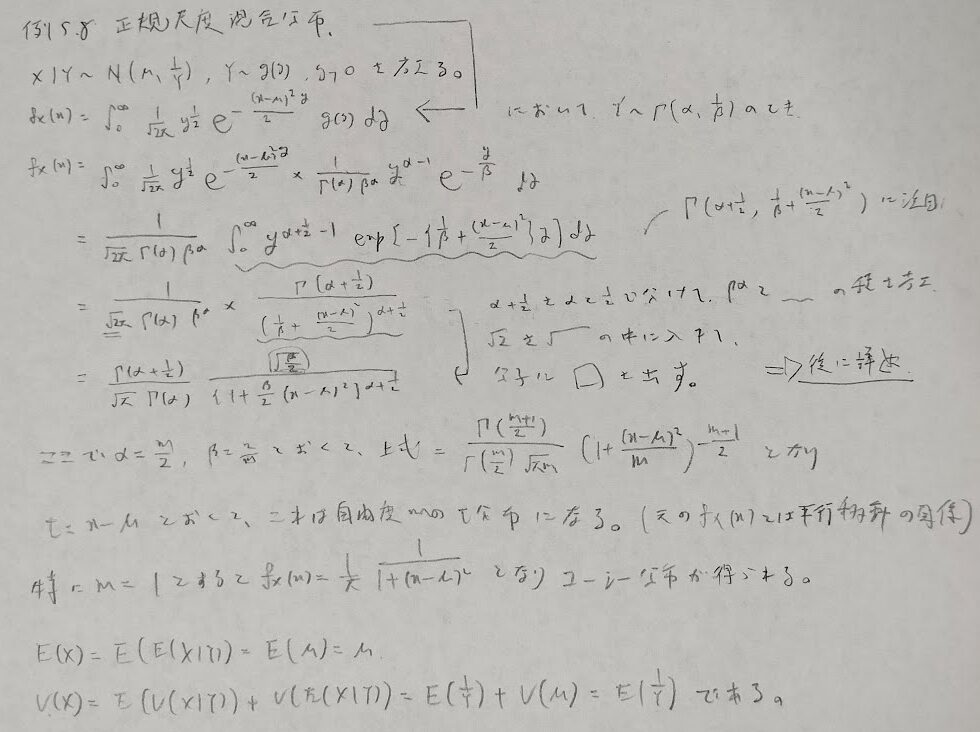
この内容の途中での式変形を下記に載せます。
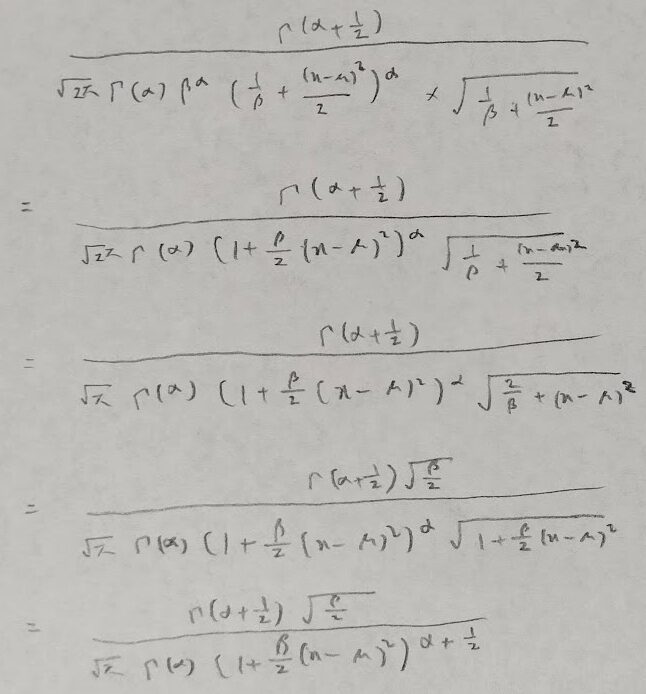
次にガンマ・ポアソン分布です。ポアソン分布が期待値と分散が等しくなりますが、実際は分散の方が期待値より大きい場合が出てきます。これを過分散の問題といいますが、これを解消する分布になります。また負の二項分布とも関連性があります。
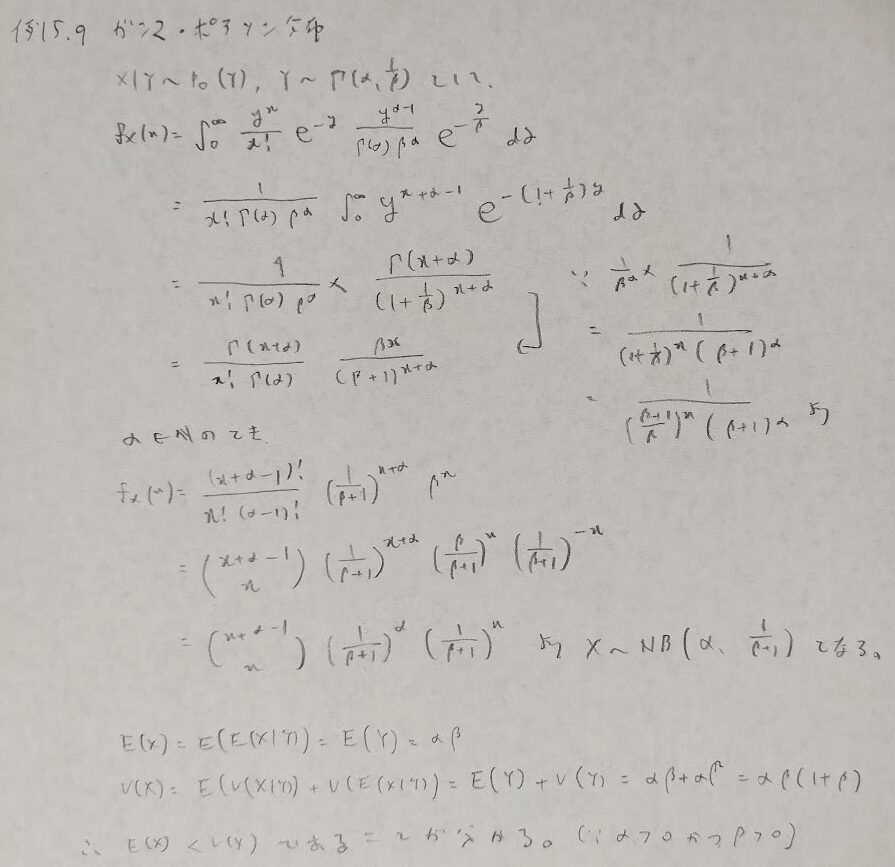
次はベータ・二項分布です。基本的に分布関数(ベータ・二項分布など)を求める際に、積分を用いるのでこの問題ではYの方がベータ分布に相当することが理解できると思います。
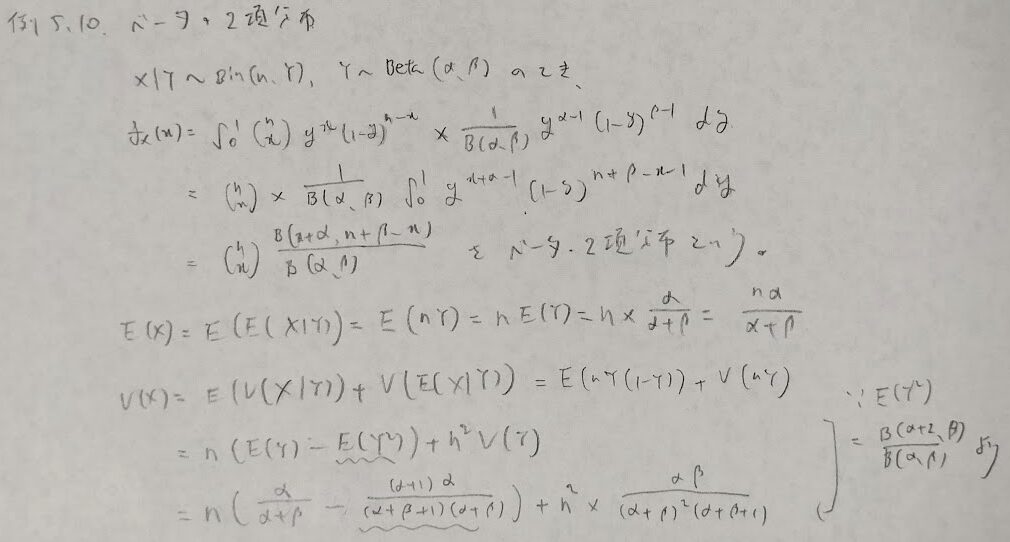
ベータ分布は高次モーメントの計算がとてもしやすいことで有名です。しかし2次のモーメントを回避する計算テクニックもあります。
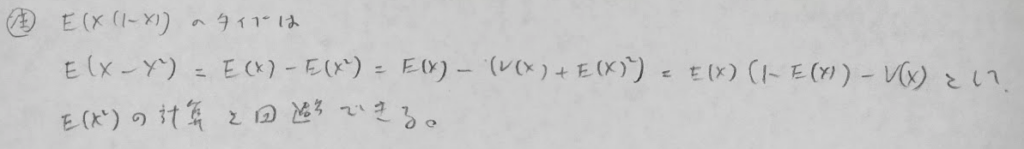
次にアクチュアリー数学で頻出の複合ポアソン分布です。
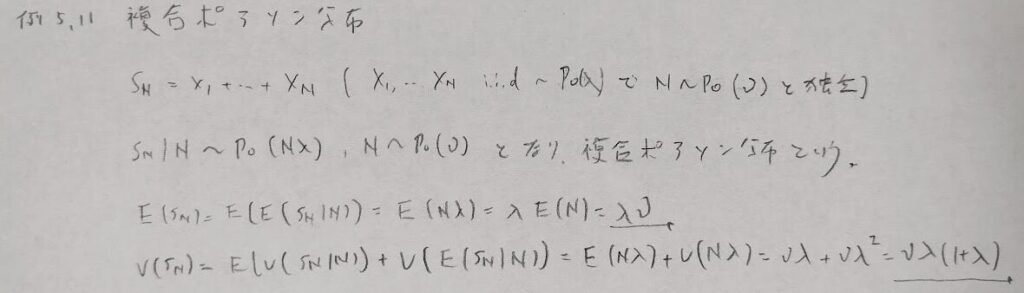
次は発展的な内容ですが、全分散公式の一般化を理解できばスッと内容が頭に入ってくるはずです。

条件付き独立の具体例をあげます。
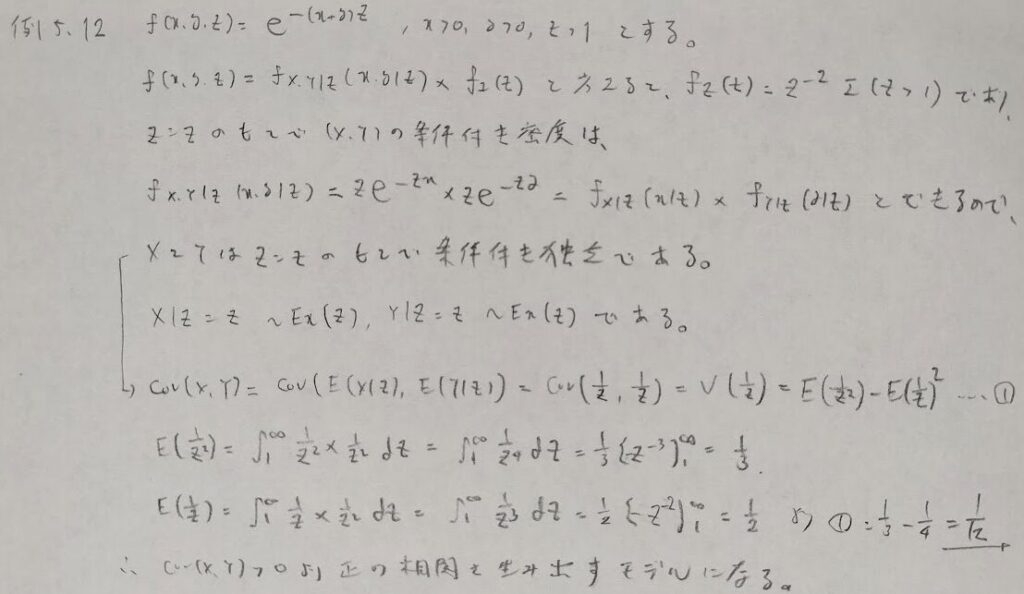
ポアソン過程
最後に確率過程を学びます。ポアソン過程を例にとります。
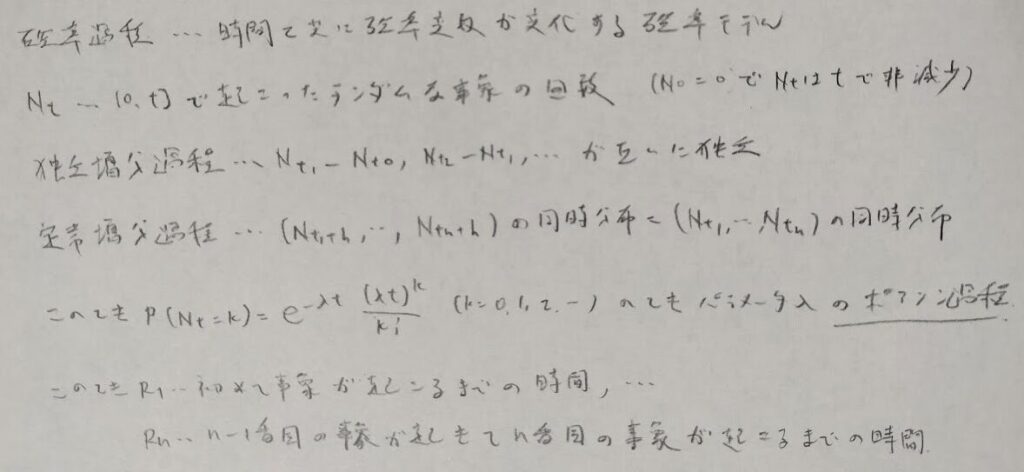
ポアソン過程はガンマ分布と密接な関係があります。確率間の言い換えもできるようになると素晴らしいですね。これが(4)の証明のポイントです。

統計検定1級青本の第5章の問題
順序統計量とベータ分布の関連については岩沢先生の『リスクを知るための確率・統計入門』がとてもわかりやいです。今まで参考にしてきた書籍の中でピカイチのわかりやすさでした。
問1:順序統計量と範囲の分布

問2:ベータ分布に帰着

問3:順序統計量と指数分布
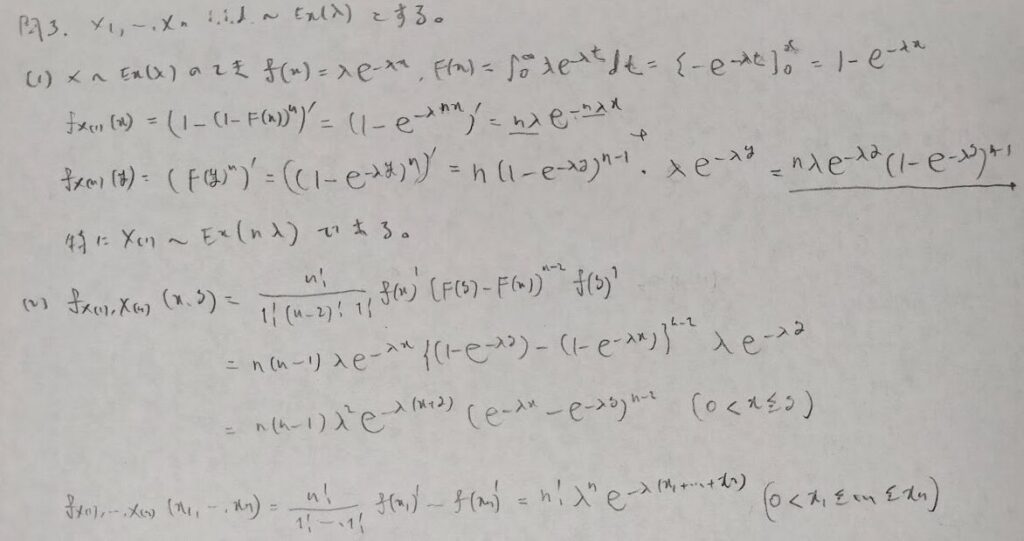
問4:一様分布と順序統計量
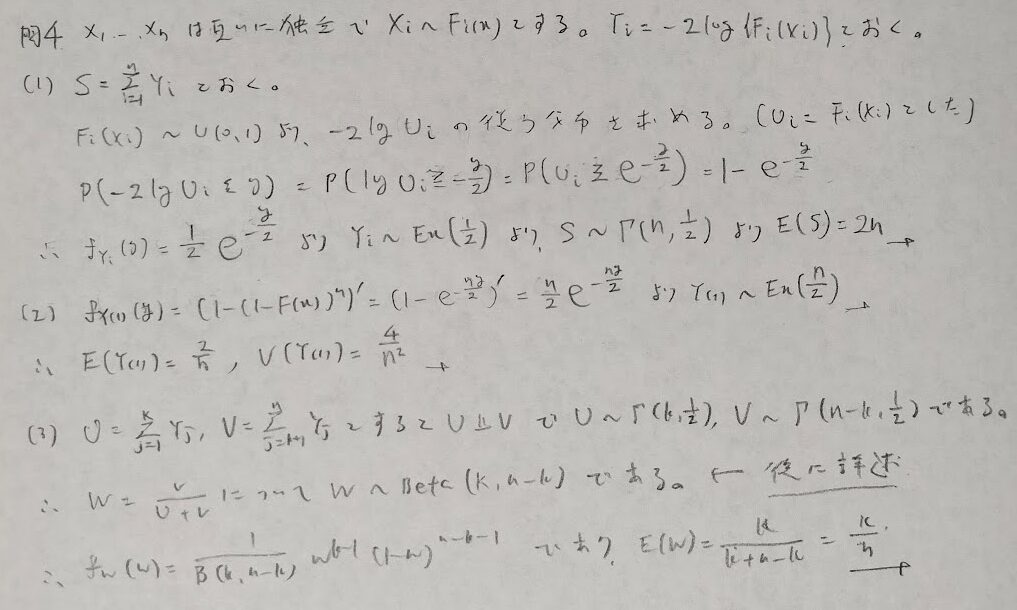

問5:ガンマ・ポアソン分布の積率母関数

問6:二項・二項モデル

問7:複合ポアソン分布の積率母関数
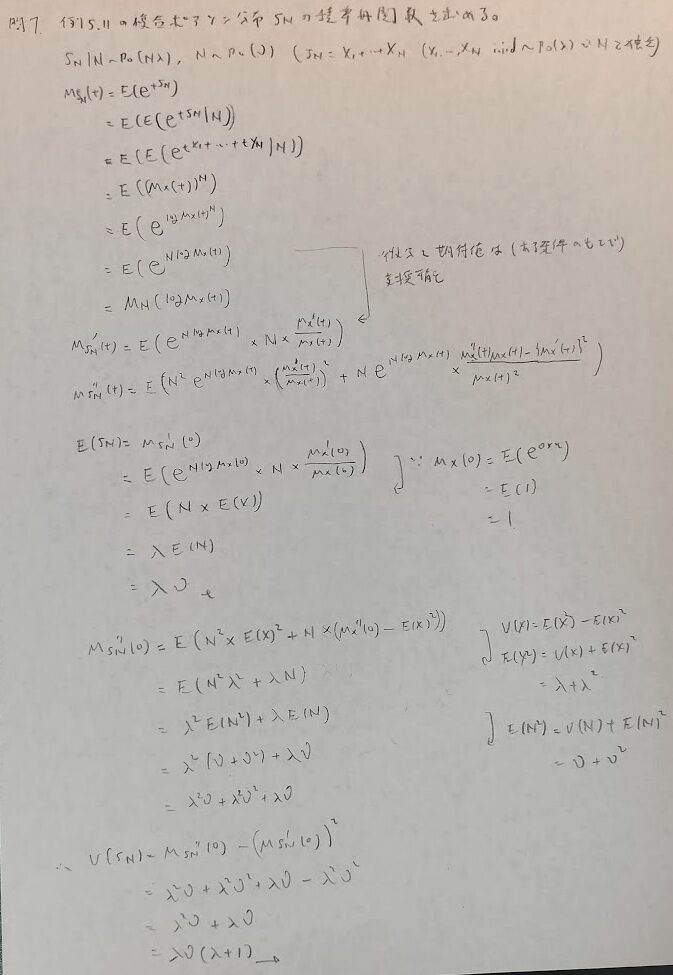
問8:条件付き共分散の公式証明

問9:条件付き分散
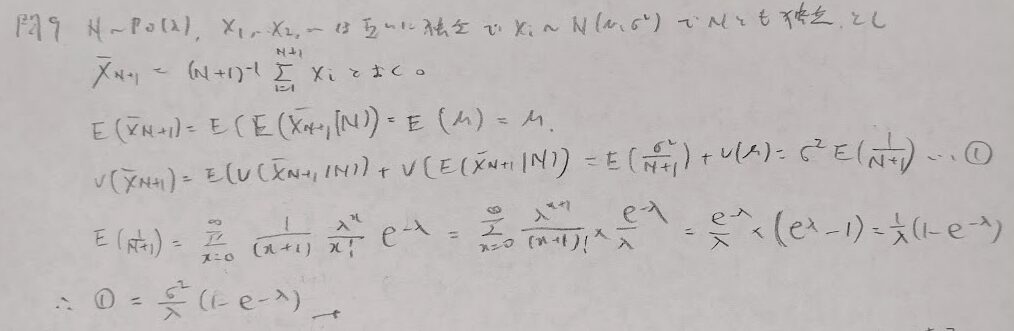
なんだか突然難易度が下がった感じで少しホッとしました。
問10:3変数の同時確率(密度)を経由する問題

問11:条件付き独立の証明問題

以上になります。前章と比べると問題数は少ないですが、その分だけ良問がギュッと詰まった内容でした。
最後に本記事で参考にした書籍を紹介します。『リスクを知るための確率・統計入門』は順序統計量周辺で参考にしました。アクチュアリー数学と相性がとても良いので、受験を考えている方には特におすすめできます!
そしてメイン本である『データ解析のための数理統計入門』は統計検定1級の新たなバイブルと呼ばれつつある名著です。統計検定準1級レベルと公式には書かれていますが、統計検定1級対策の方がさらに相性が良い書籍だと感じています。










