アクチュアリー数学の確率分野の対策の指定教材である『確率統計演習 1 確率』の変数変換の章の問題の解説を行います。
各章の解説記事のリンクをまとめておきますね!
第1章:事象と確率
第2章:確率変数と分布
第3章:平均値、分散
第4章:変数変換と和の分布
第5章:積率と積率母関数
第6章:大数の法則と中心極限定理
問題を解いていて思いましたが、本記事の内容は統計検定1級の対策にも有効です。統計検定を受験する方も是非ご活用ください。
本記事の確率密度関数の取りうる値について、微分を用いていくことにより定義域からイコールを除いた方が良いと考えて途中から端点を抜かしています。実際1点での取りうる確率は0なので問題ありません。
『国沢確率』第4章「変数変換と和の期待値」の例題

途中、平均値の定理を用いていますが、微分の定義式から高次の項を無視するということです。
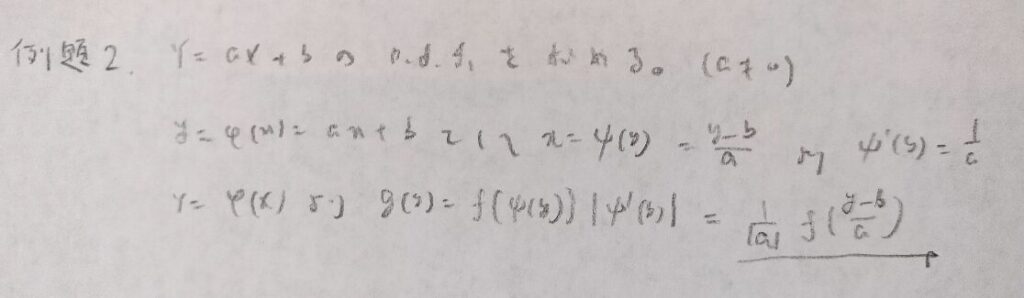

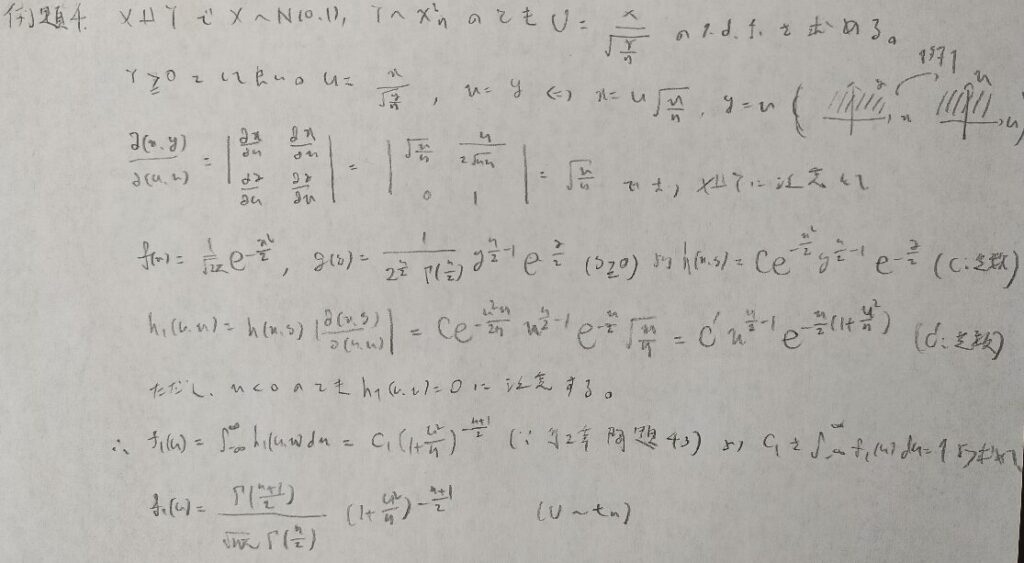
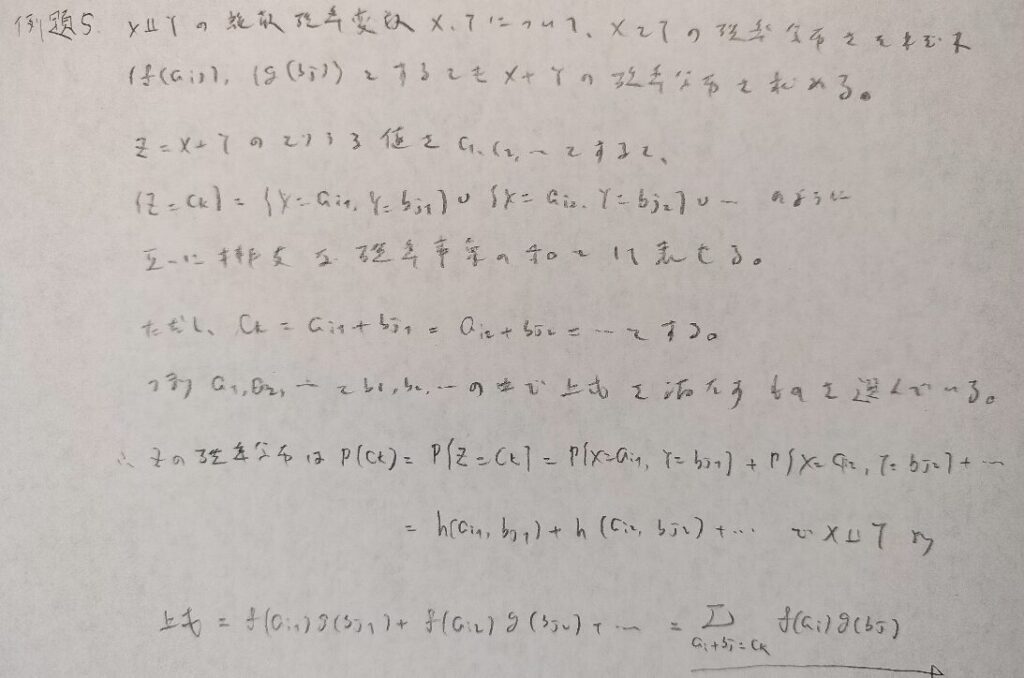
よく使われる式ですが学習者にとって盲点となっている部分です。
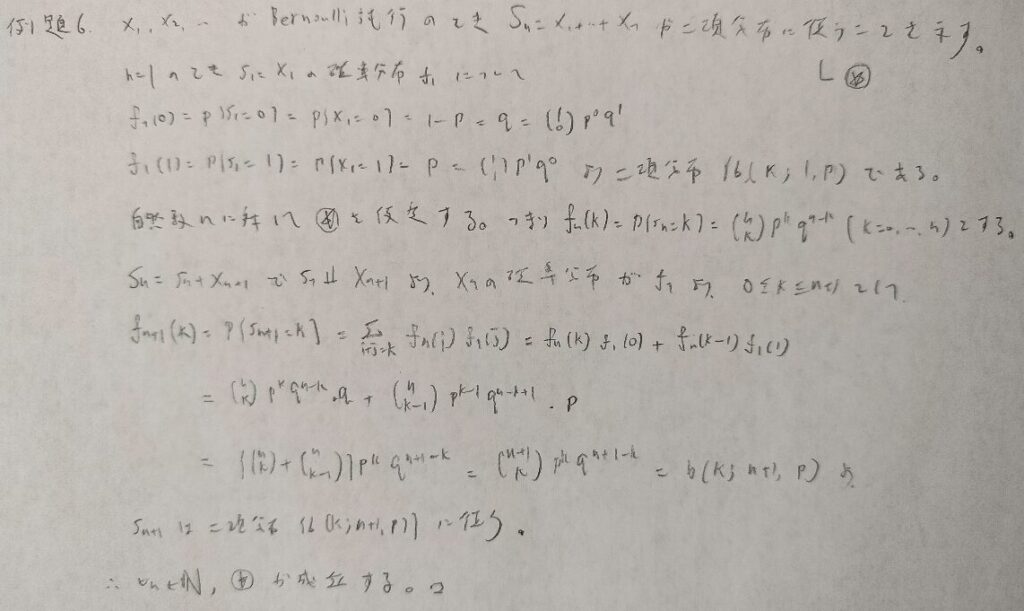
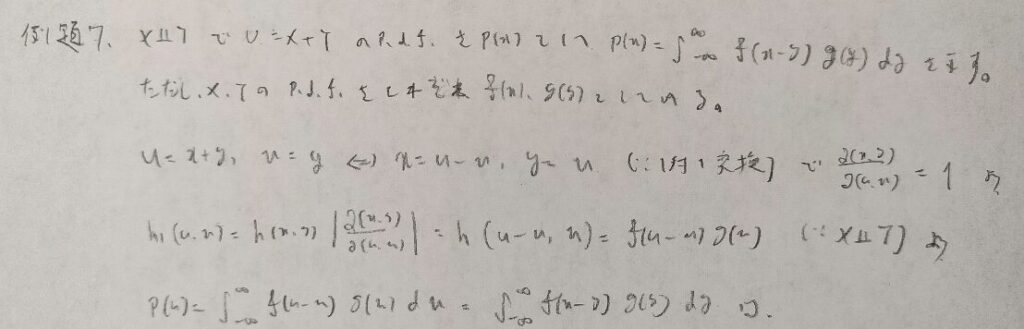
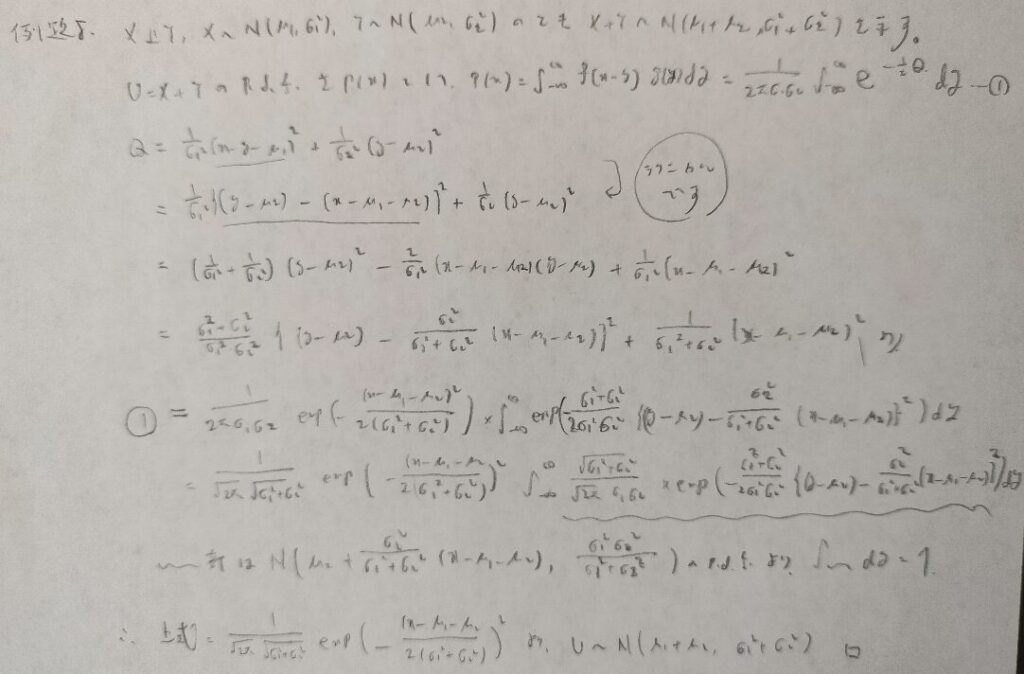


難問です。とにかく計算量が多いので式変形の過程を追いましょう!
アクチュアリー数学の試験では結果を覚えておきたいところですね!
『国沢確率』第4章「変数変換と和の期待値」の問題
第4章の問題では『確率統計演習 1 確率』の例題で学習した内容を既知として用いていきます。
問題数は他の章と比べて少なめですので一気に頑張りましょう!
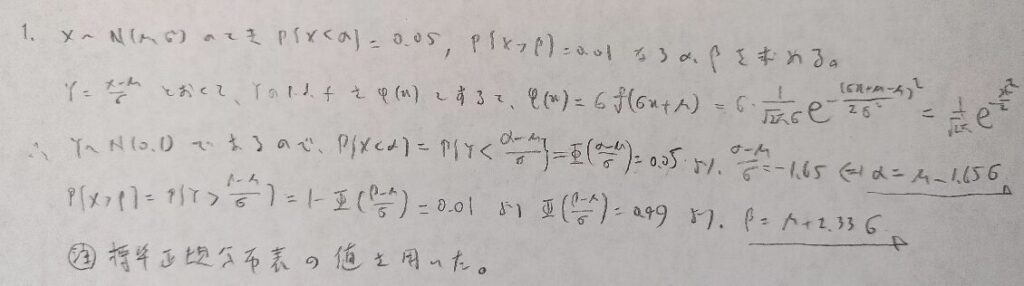
統計検定2級レベルの問題でまずはウォーミングアップです。
統計検定2級の合格法はこちらで詳しく説明されています!


平均値の定理より〜の部分は例題1の解説と同様の意味で用いています。
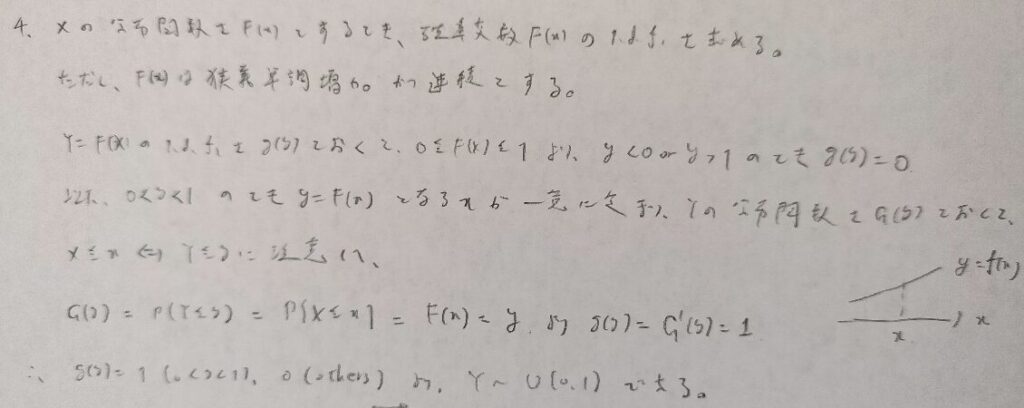
ほとんどの参考書に載っている分布関数に関する超有名問題です!

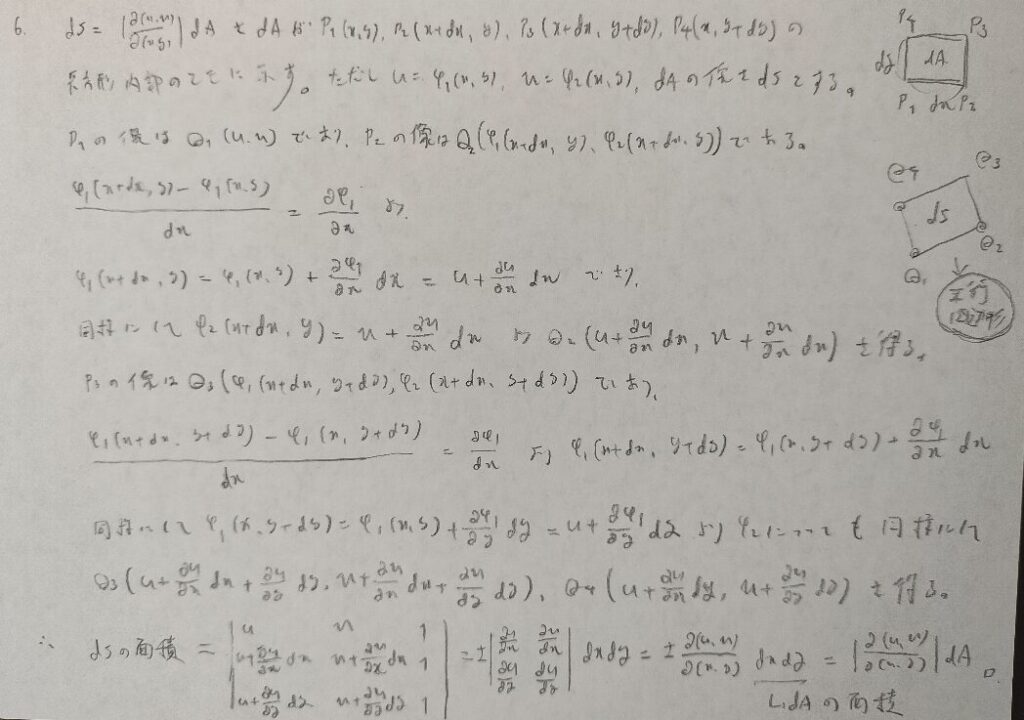
ヤコビアンの導出に関する問題です。『微分積分キャンパス・ゼミ』によりエレガントな証明が載っています。
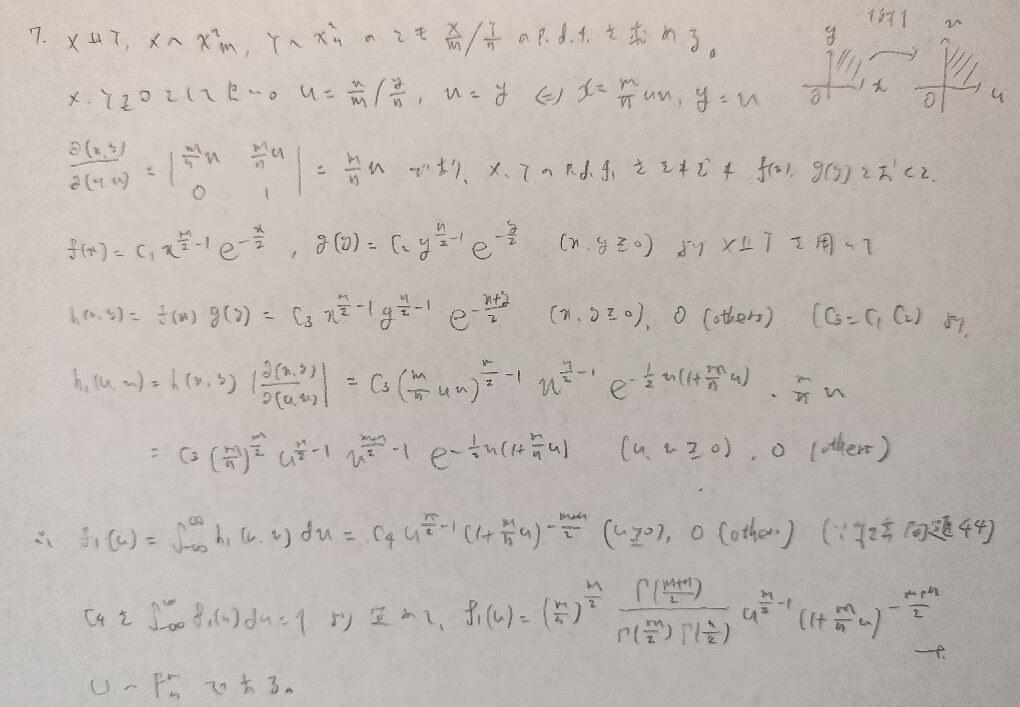
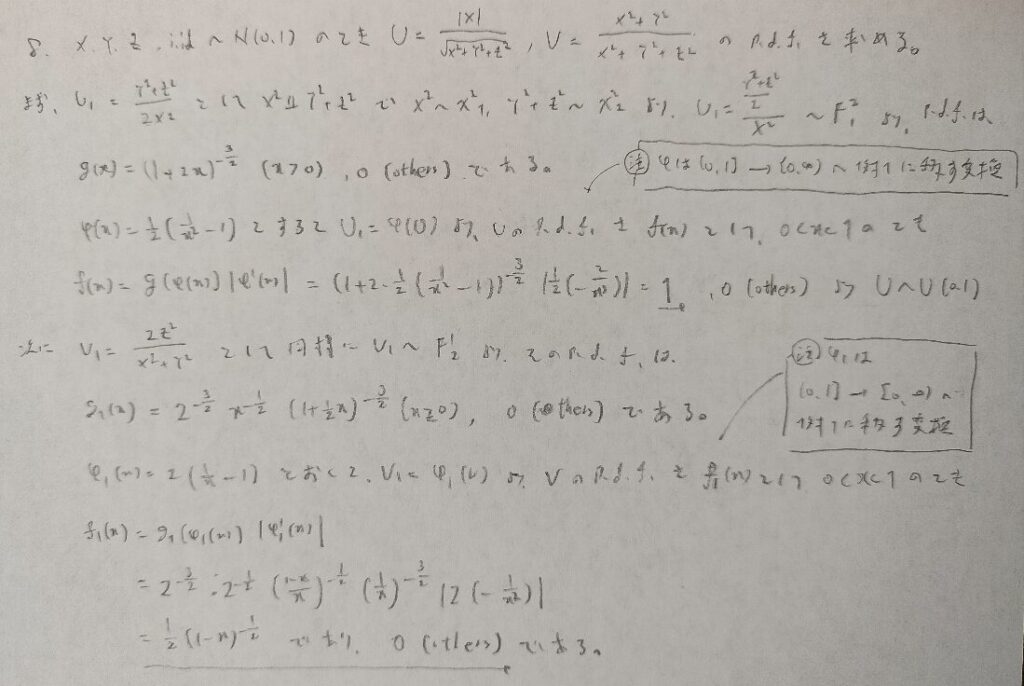
難問です。どこが難しいかと言いますと、変換する関数の設定です。初見では解くのにかなりの時間を要するでしょう。アクチュアリー数学にも類題がありますが、ここまで気づきにくい設定ではありません。
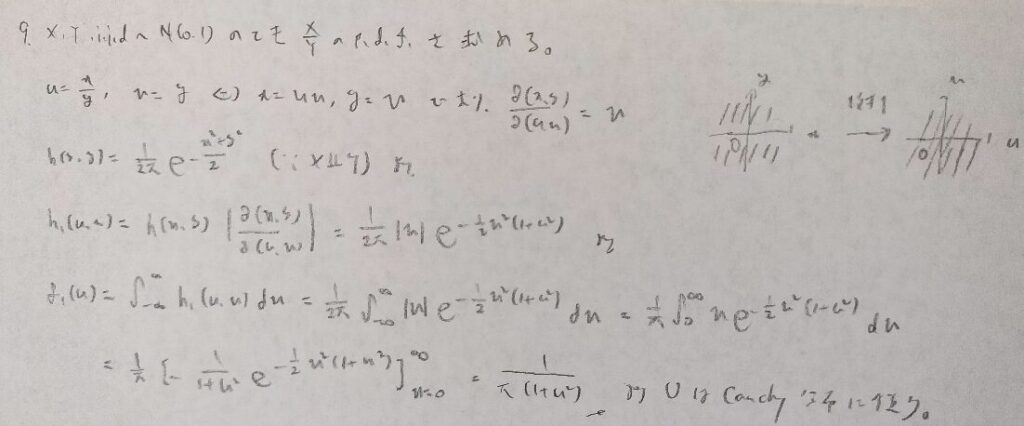
変換前のxy平面ではx軸を除く部分が斜線となっています。
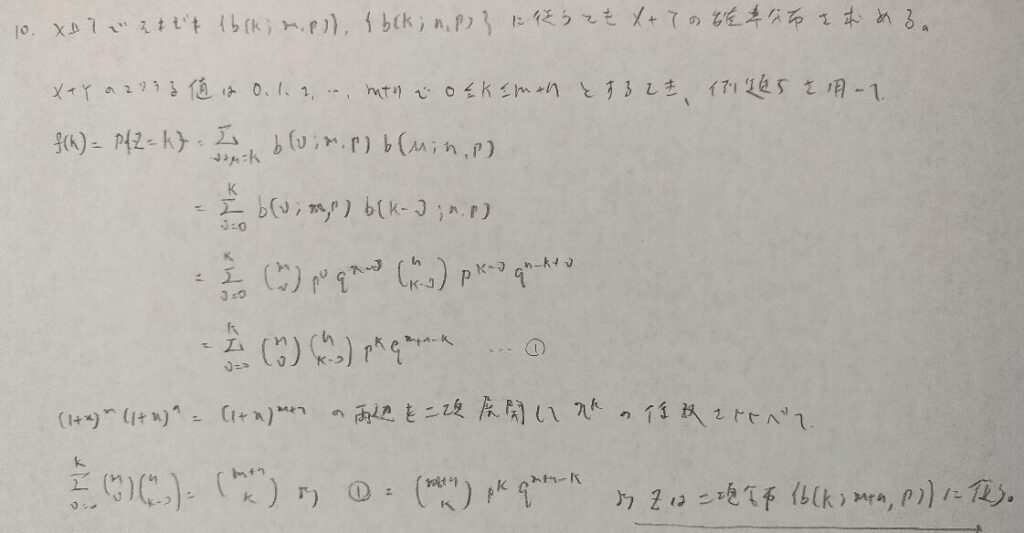
例題5を用いないと証明できないです。最後の二項展開の部分も初見では難しい感じがありますね。
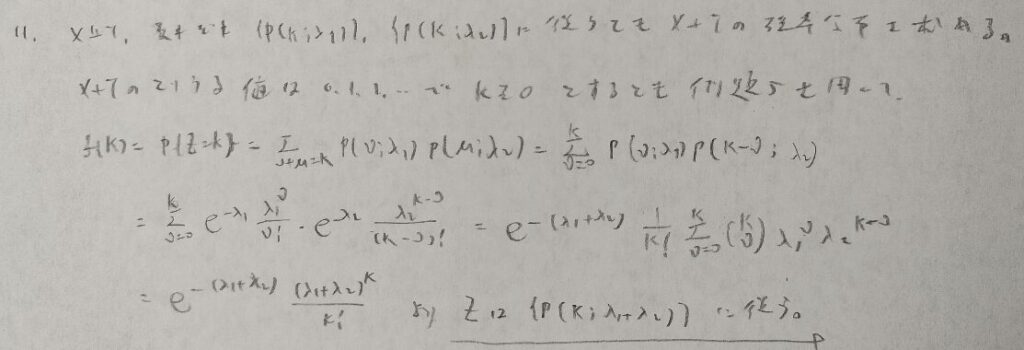
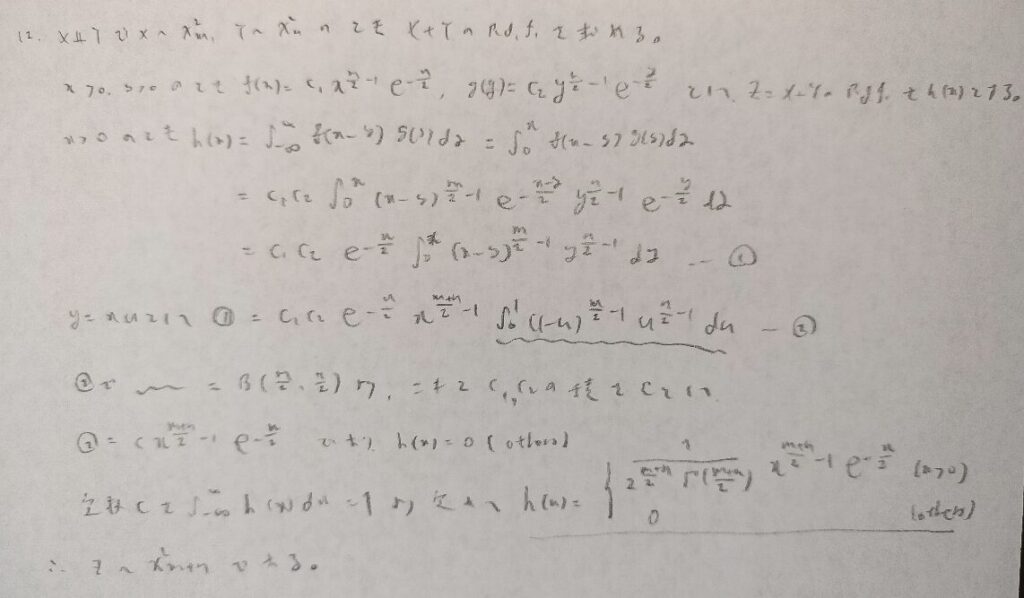
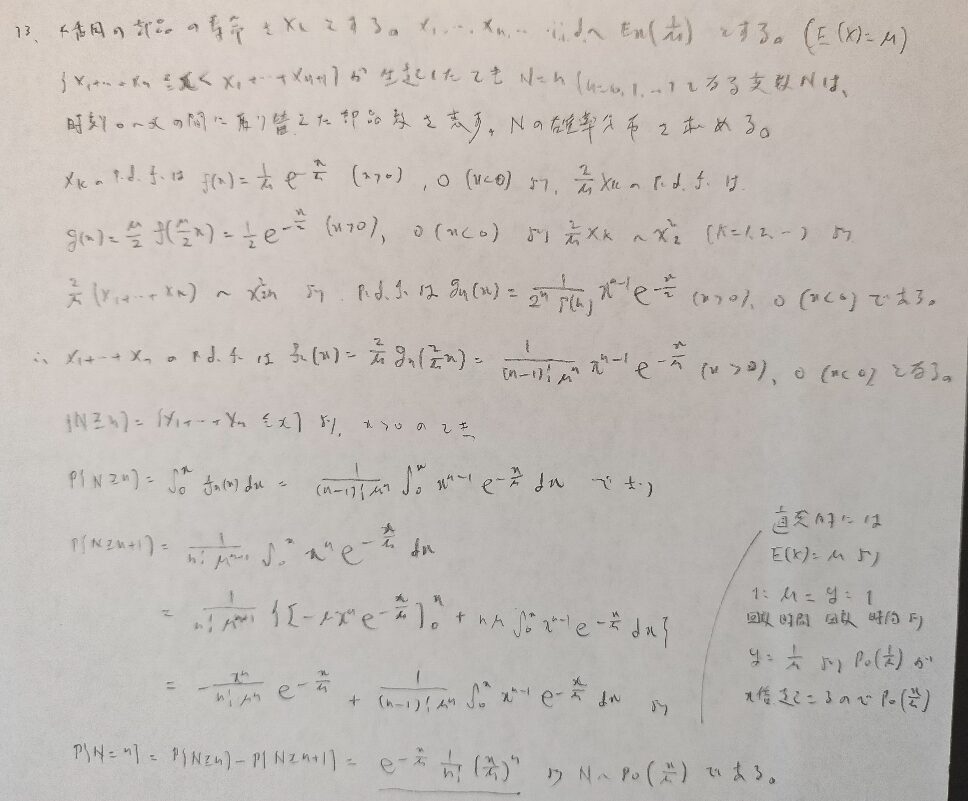
とても重要な問題です。これ系の問題の中では『確率統計演習 1 確率』の本問題の問題設定が最もわかりやすいと感じます。
より詳しい説明は指数分布とポアソン分布の各記事をご参照くださいね!

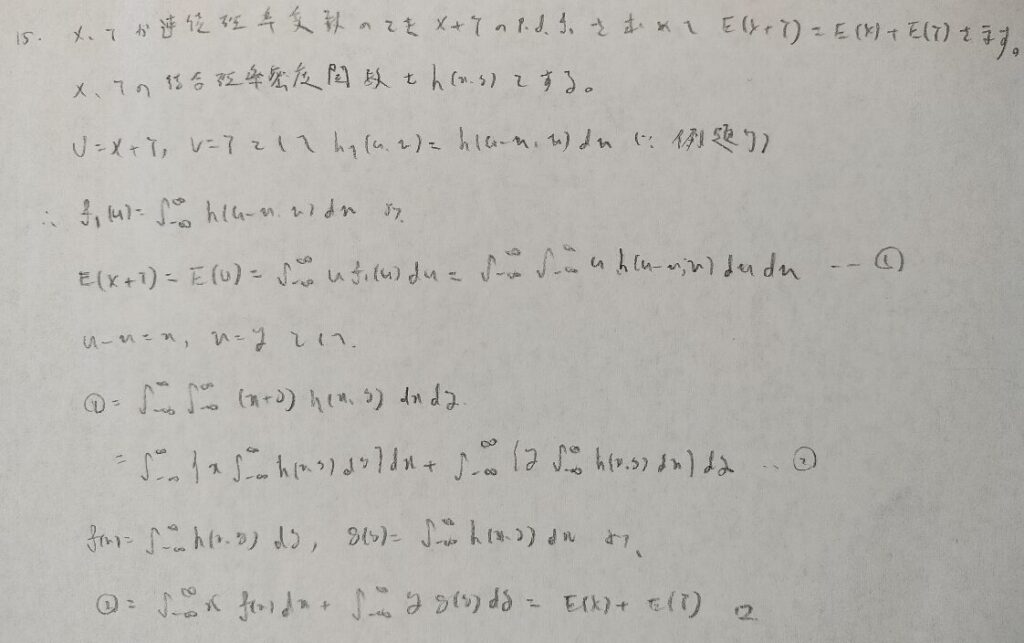
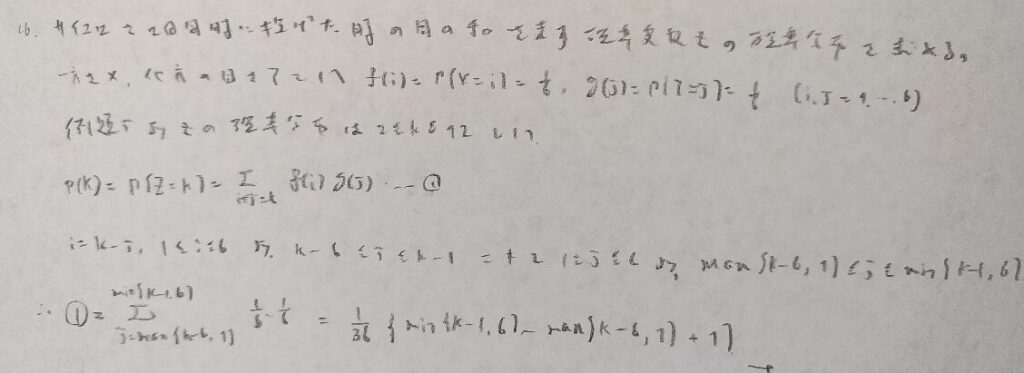
高校数学にある問題をしっかりと考えると、このような結果になるのですね。
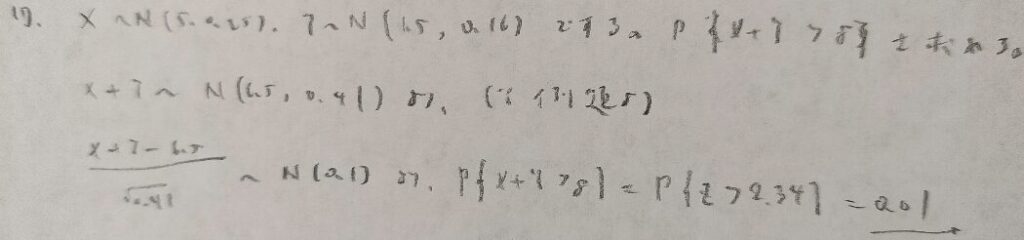

アクチュアリー数学で何度か出題されている丸め誤差の問題です。
『確率統計演習 1 確率』では一気に解いていますが、積分の時点で場合分けをしていく別解もあります。
『明解演習 数理統計 (明解演習シリーズ 3)』ではその方法で解いていますよね。
以上で『確率統計演習 1 確率』の第4章の問題が全て終了しました。終盤は分布の再生性に関する問題が目立ち、他の章と比べて全体的に難易度は低いと感じましたがいかがでしょうか。一方でヤコビアンに関する根本的な問題などもあり、そこら辺の出題は難しいと感じたと思います。
次回(こちらです)はいよいよ積率母関数に関する内容です。『確率統計演習 1 確率』を片手に一緒に頑張りましょう!



