統計検定1級の新たなバイブルとして青本という名前で親しまれている久保川先生の『データ解析のための数理統計入門』を第1章から自力で解いていき、皆様と共に注意すべき箇所などをまとめた記事になります。本章では確率分布が登場することから、過去記事の引用も積極的に行なっていきます。
不明な箇所がありましたら、是非とも過去記事も併せて学習されてください。体系的に書かれておりますので、理解が深まると思います。
∩∪⊂∈←よく使う集合記号です。
本書が類書と良い意味で異なる点は期待値や分散の導出がわかりやすい方法で書かれている点です。万が一公式を忘れてしまっても復元しやすい方法で説明されています。また特に第2章で感じたことですが、本書は統計検定準1級レベルの演習書というより統計検定1級の問題とほぼ等価の計算量の問題が多いと感じました。とてもおすすめです。
統計検定1級向けの基本事項の総整理
統計検定1級の過去問でよく見るタイプの問題を抜粋して各分布の基本について順に復習していきます。離散型確率分布→連続型確率分布の順に進んでいきます。
二項分布
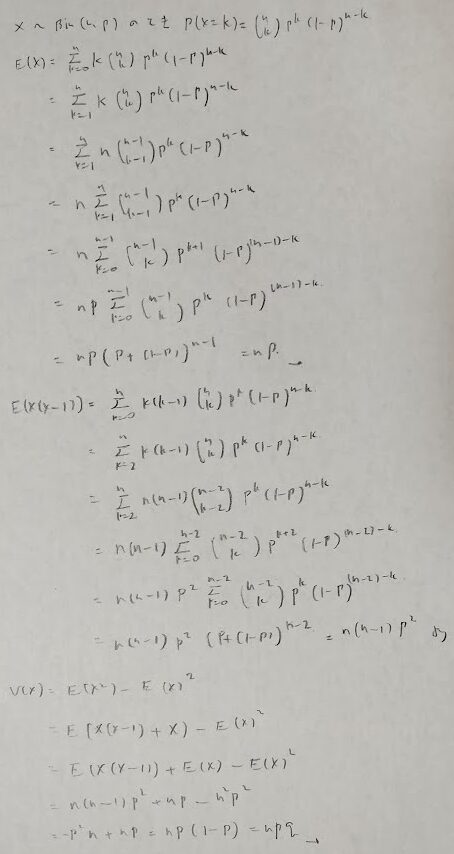
統計検定1級で何度も問われているため、何も考えずに導出できるように訓練しておきたいところです。
負の二項分布
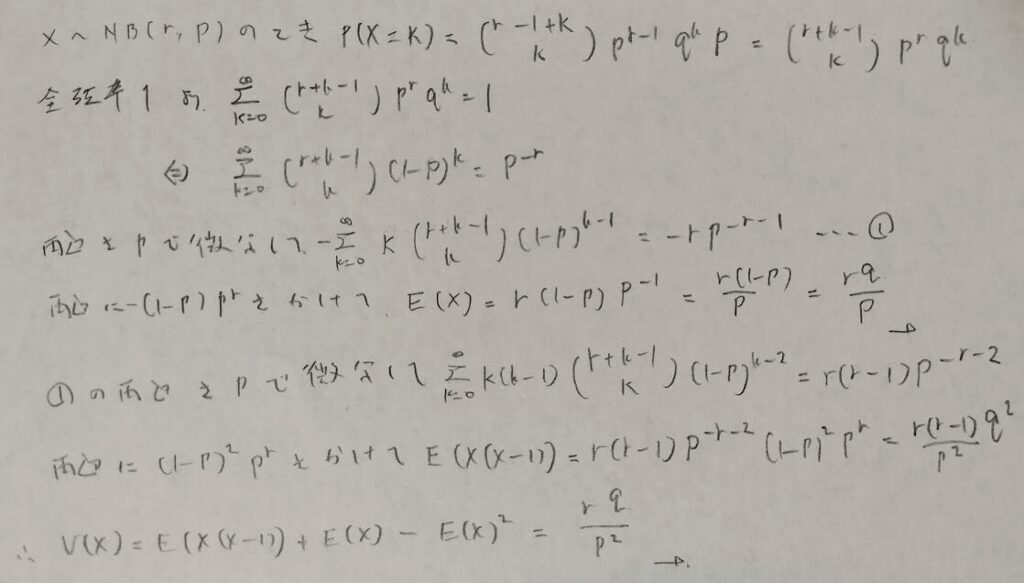
負の二項分布については一度やっておかないと本番で思いつくような簡単さではありません。
ポアソン分布
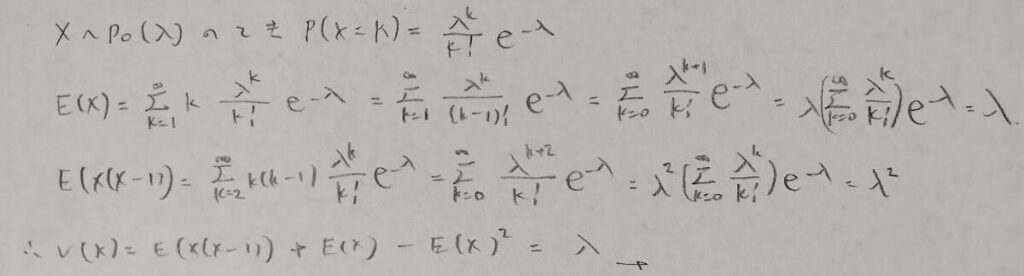
二項分布と並んで統計検定1級で頻出度が高い分布です。こちらも無意識のうちにでも導出できるように訓練しておかないといけません。
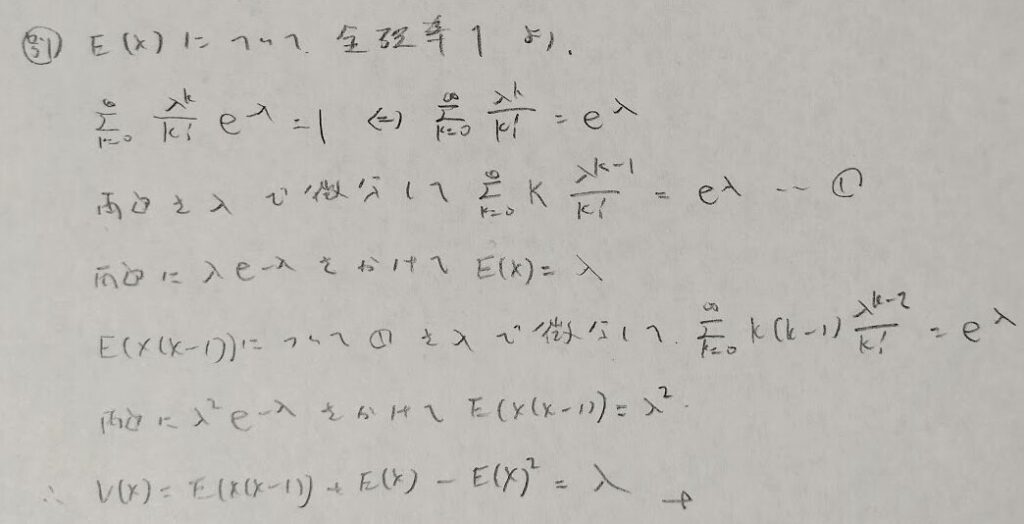
『データ解析のための数理統計入門』ではユニークな導出法として上の方法が紹介されておりました。負の二項分布の内容と照らし合わせても一貫線のある導出法です。
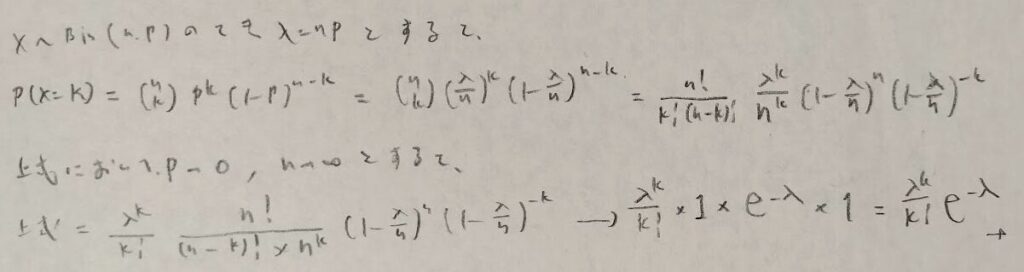
簡単すぎるかも知れませんが、二項分布からポアソン分布が導かれる過程を再度紹介させていただきました。第2章の演習問題の最後の問題でこの導出の発展版が登場します。
超幾何分布

赤玉をX個とするとき、Xの定義域は次のようになります。
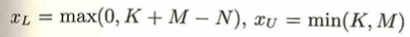
ガンマ分布
連続型確率分布においても、ガンマ分布や正規分布などで全確率1から期待値や分散を導出する際は、パラメータで微分して両辺に定数を掛ける作業を行います。類書にはあまり書かれていないテクニックで『データ解析のための数理統計入門』でのみ学べる内容となります。
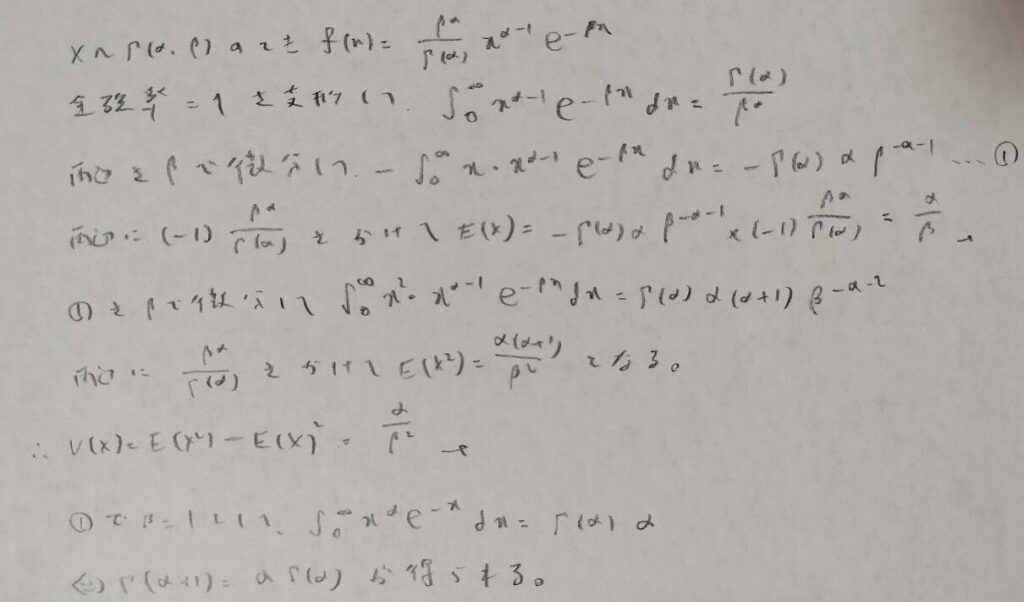
ベータ分布
ベータ分布で2つのパラメータを1とするとU(0,1)になります。U〜U(0,1)とするとき、YをXの分布関数とするとY〜Uです。
正規分布
意外かも知れませんが、このような導出方法では正規分布がなかなか難し目ですのでご紹介します。
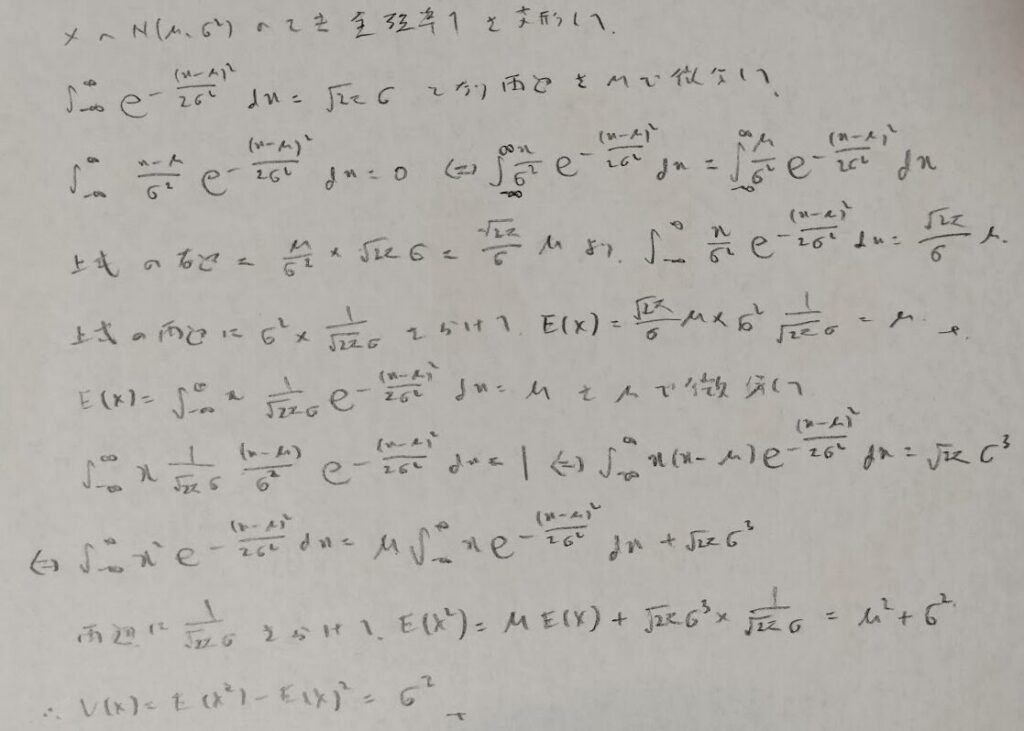
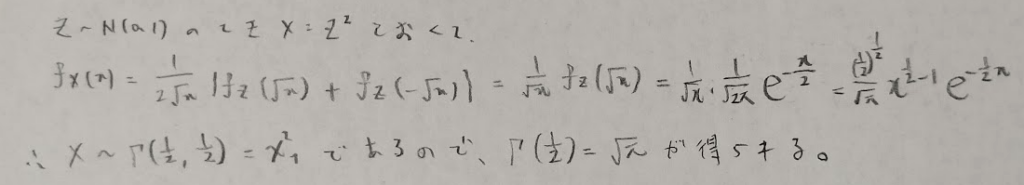
『データ解析のための数理統計入門』では演習問題に入る直前の内容でΓ(1/2)の値について触れられております。とても感銘を受けましたのでご紹介させていただきました。
演習問題
『データ解析のための数理統計入門』の第2章の演習問題を解きましたので掲載します。最後の方は統計検定1級で出題された場合はなかなか難しめの問題になります。本書はアクチュアリー数学や統計検定1級の統計応用の理工学で出題される一様乱数を用いた逆関数法にも踏み込んでおり、かなり実践を想定した問題揃いとなっております。
二項分布のモード
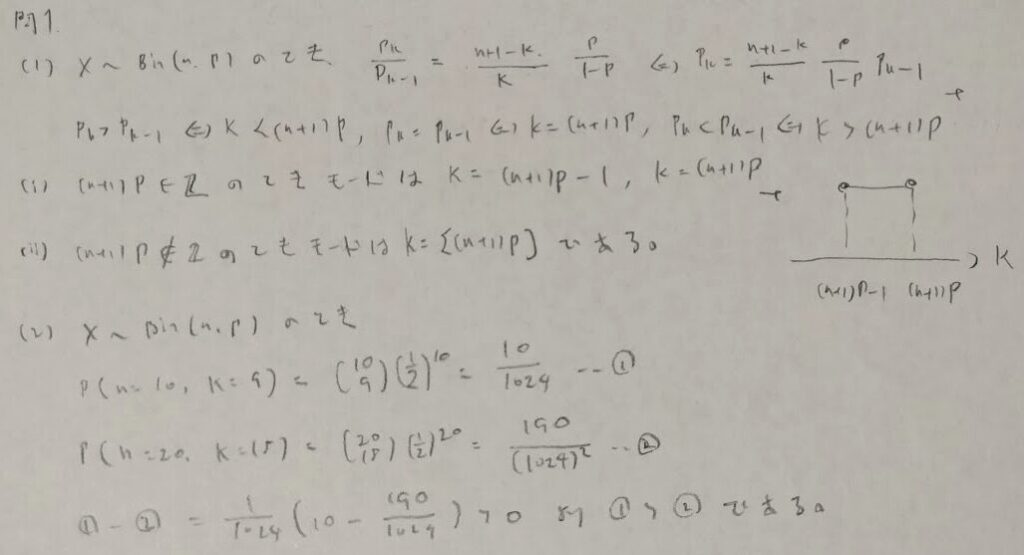
ガウス記号が入った場合の評価の仕方は瞬時に出てくるようにしましょう!!
ポアソン分布のモード

幾何分布と不等式
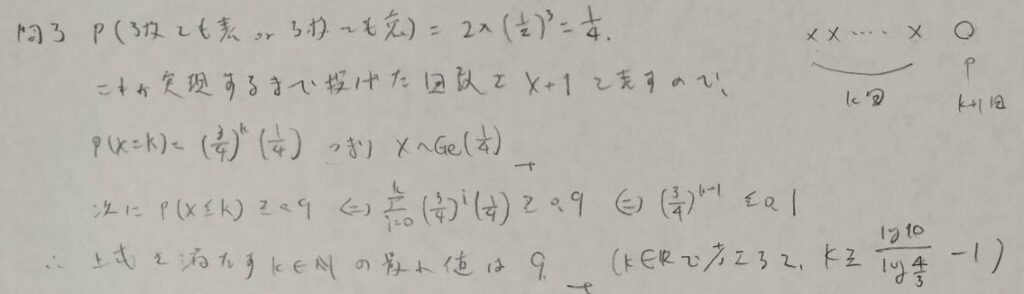
一様分布と離散一様分布の関係
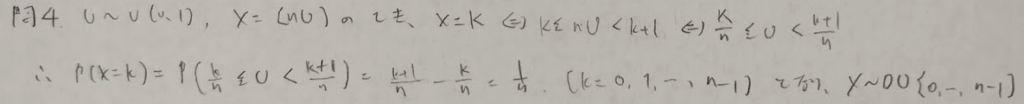
指数分布と幾何分布の関係

正規分布表
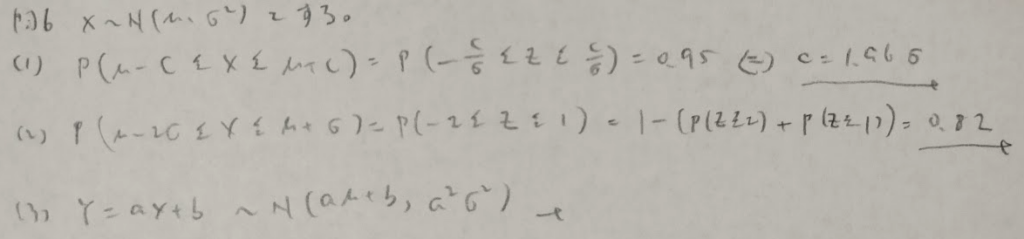
正規分布とカイ2乗分布とコーシー分布の関係
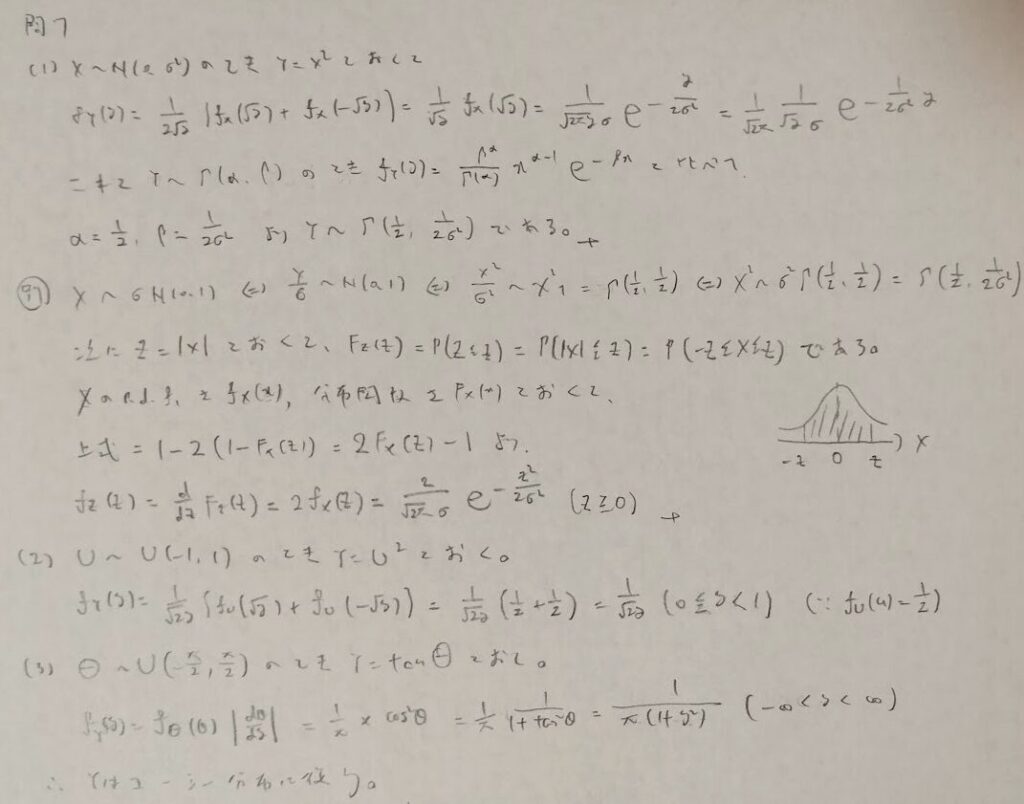
逆関数法
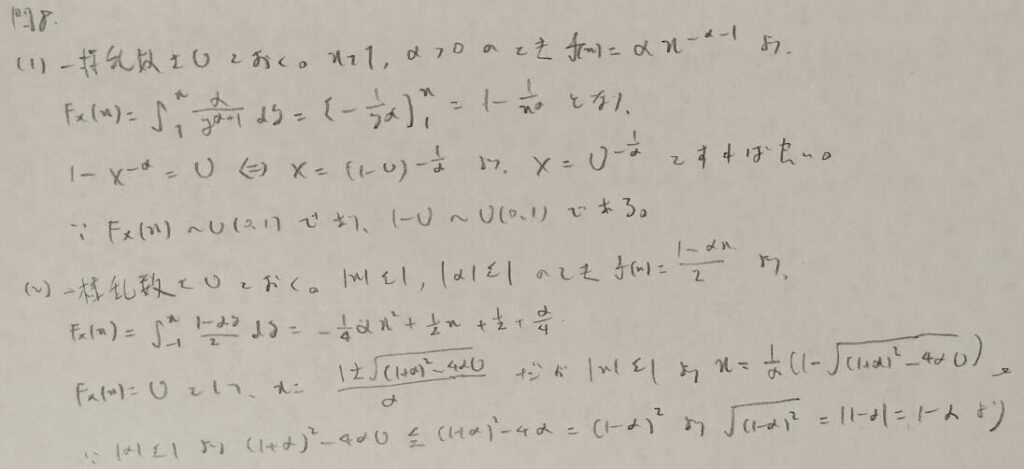
ロジスティック分布の対称性
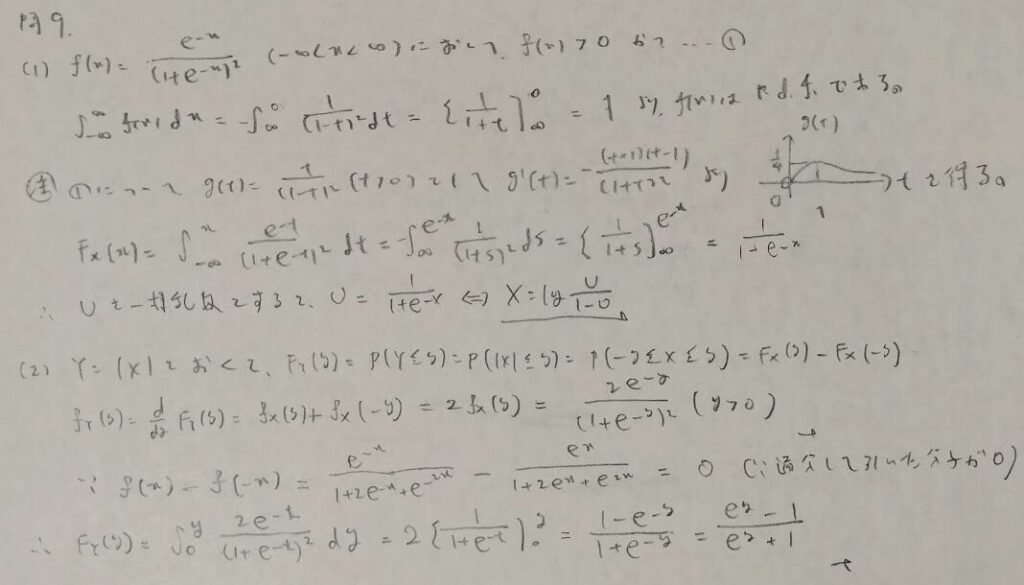
パレート分布のハザード関数
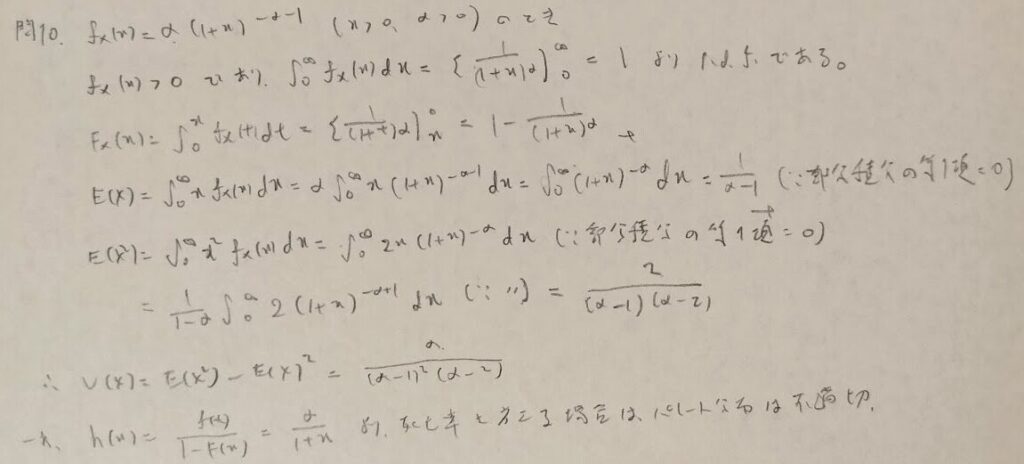
ラプラス分布と対称性

幾何分布と極限値
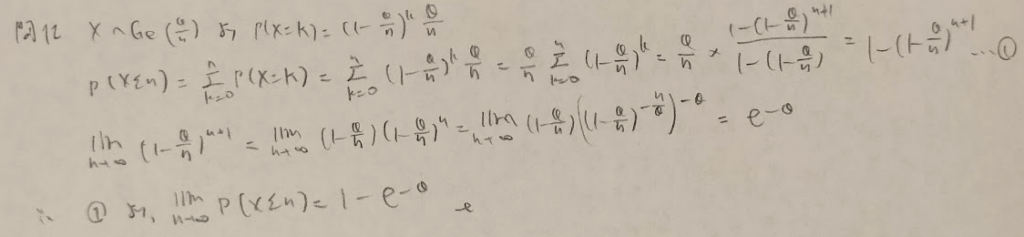
ポアソン分布と微分方程式
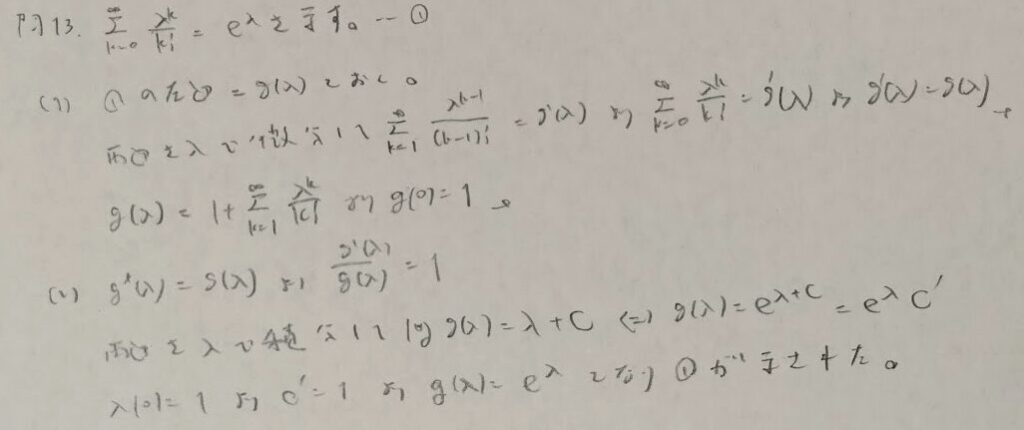
負の二項分布の全確率1の証明
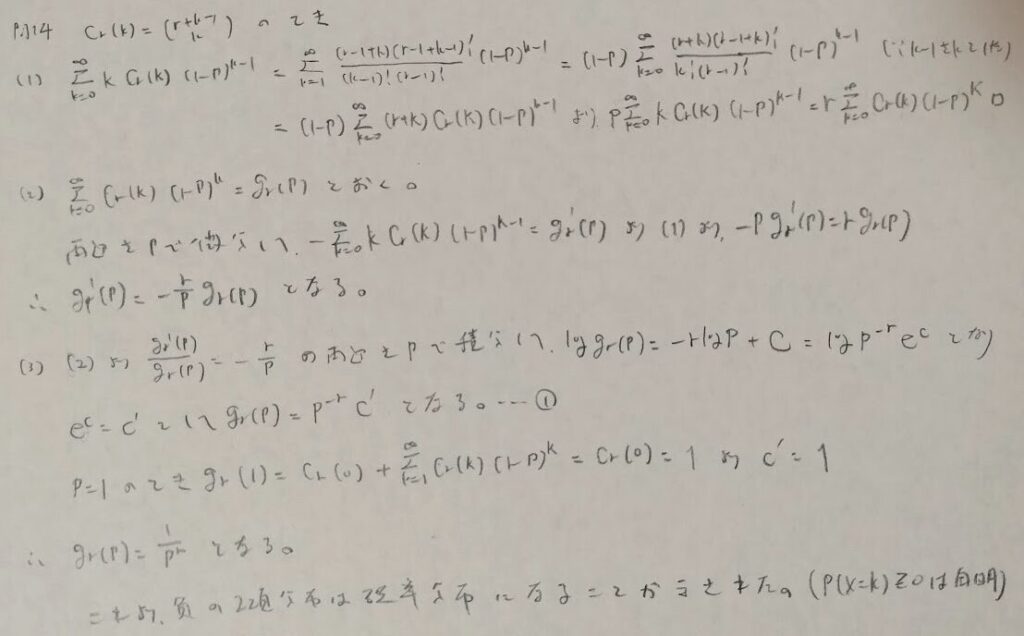
この本『現代数理統計学の基礎(共立講座 数学の魅力 11)』に一般的な導出法が記載されています。
この本は統計検定1級のバイブルとも言われている本ですね!
ガンマ分布とガンマ関数
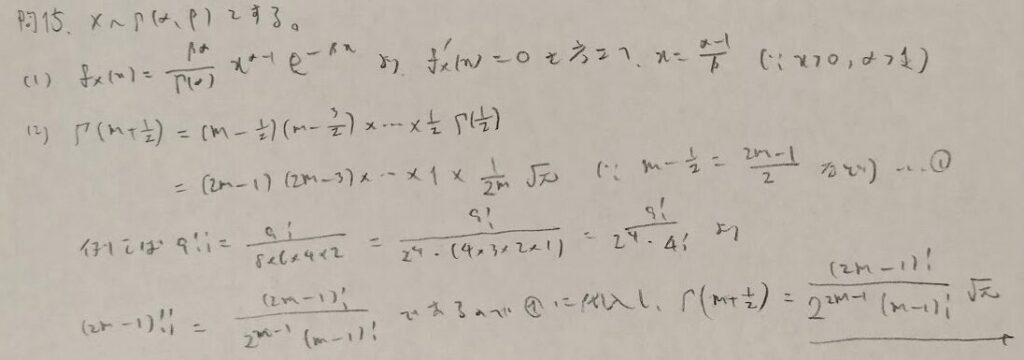
コーシー分布の期待値について
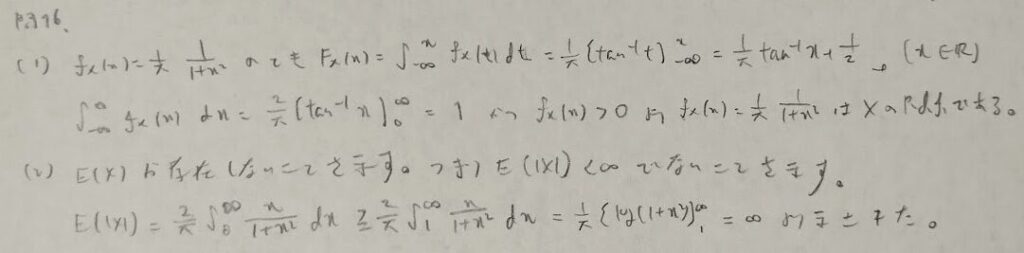
超幾何分布と二項分布の関係

『データ解析のための数理統計入門』の第2章の解説は以上になります。とても良い問題が多く勉強になりますよね。
『データ解析のための数理統計入門』は読んでいてハッとさせられる気づきが多い本ですよね。次回も楽しみですね!